由关系式引发的思考与教学启示

陕西 党维军 成均武

一、创设情境、问题导入

教师创设情境、提出问题：假如你站在地球赤道上，地球自转越来越快，你会有什么感觉？

学生可能回答出三种答案：(1)重力或对地面的压力越来越小；(2)重力或对地面的压力为零，处于漂浮状态；(3)发生离心现象被“甩”离地球。

教师总结：可见，随着地球自转的加快，会发生一系列有趣的现象，这节课我们以匀质球形自转天体为模型，运用所学的物理知识来研究这些有趣的现象。

二、三类问题的呈现及解析

1.球形天体自转引起漂浮的临界周期问题

【例1】一物体静置在平均密度为ρ的球形天体表面的赤道上。已知万有引力常量为G，若由于天体自转使物体对天体表面压力恰好为零，则天体自转周期为

( )

【思路点拨】本题考查球形自转天体赤道上物体漂浮的临界周期。万有引力对赤道上物体产生两个作用效果，一是提供物体随天体自转的向心力，二是使物体具有重力。自转越快(周期越小)物体需要的自转向心力越大，重力越小。若自转向心力恰好等于万有引力，则物体的重力恰好为零，即赤道处重力加速度为零，物体处于漂浮状态，对天体表面压力恰好为零。

2.球形天体稳定自转的临界密度问题

【例2】2018年2月，我国500 m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”，其自转周期T=5.19 m/s，假设星体为质量均匀分布的球体，已知万有引力常量为6.67×10-11N·m2/kg2。以周期T稳定自转的星体的密度最小值约为

( )

A.5×109kg/m3B.5×1012kg/m3

C.5×1015kg/m3D.5×1018kg/m3

【思路点拨】本题考查球形天体稳定自转的临界密度问题。天体的自转是同轴转动模型，各点角速度和周期相同，赤道处物体绕轴圆周运动的半径最大，需要的向心力最大，最容易发生漂浮现象。在自转周期一定的条件下，要保证天体稳定自转，即不发生离心现象，须满足条件：赤道处物体需要的自转向心力不超过星体提供的万有引力，据此关系可得满足条件的密度。

3.近地卫星环绕周期与天体密度的关系

【例3】若一均匀球形星体的密度为ρ，万有引力常量为G，则在该星体表面附近沿圆轨道绕其运动的卫星的周期是

( )

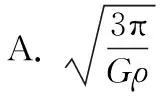
【思路点拨】利用圆轨道卫星的环绕周期和轨道半径，根据万有引力提供向心力，可以计算中心天体的质量，当卫星近地环绕时，轨道半径与中心天体的半径相同，会出现一种特殊情况，即跳过质量直接计算出中心天体的密度，这意味着天体的密度直接决定其近地卫星的环绕周期。

以上这三类问题中，例1和例3难度不大，尽量让学生自主完成，例2稍有难度，教师可以提示学生完成。

三、析殊途同归，悟物理之美

【思考问题2】从运动和受力的角度分析近地卫星和赤道上的物体有什么异同？

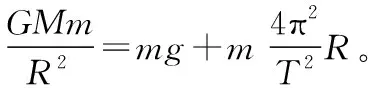
【思考问题3】例1中的临界周期与例2中的临界密度有什么关系？

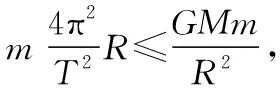
三、针对训练与拓展延伸

针对本节课的教学内容设计四道原创习题如下，以供课后针对训练和拓展延伸使用。

【针对训练1】假设地球的质量与体积不发生变化，而自转速度逐渐加快。当赤道上的物体对地面压力为零，处于漂浮状态时，地球上一昼夜的时间约为(地球半径取6 400 km)

( )

A.45 min B.85 min C.125 min D.165 min

【设计意图】该题贴近学生的生活情境，能够引发学生联想，激发学生的学习兴趣。可作为课后练习题，巩固和检测学生对本节课内容的学习效果。

【答案】B

【针对训练2】质量超过钱德拉塞卡极限的星体，电子将被压入原子核中，与其中的质子合并为中子，大量中子紧密排列构成中子星。已知某中子星的密度约为1×1018kg/m3，万有引力常量为6.67×10-11m3/kg·s2。则该中子星稳定自转的极限转速约为

( )

A.600 r/s B.1600 r/s C.2600 r/s D.3600 r/s

【设计意图】该题以中子星的形成为背景，出现宇宙学名词：钱德拉塞卡极限，引导学生了解科技前沿。考查天体稳定自转的临界周期和临界密度，同时考查转速的概念和数学运算能力。

【答案】C

【拓展延伸1】某行星的自转速度逐渐加快，当其转速为n0时，某物体在该行星两极所受重力与在赤道上所受重力的比值为4∶3，假设该行星可视为质量均匀的球体，且质量和半径不发生变化，则该行星维持稳定自转的最大转速为

( )

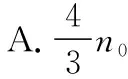
【设计意图】该题综合考查万有引力定律与圆周运动的规律，要能分析极地和赤道处重力加速度的差异，知道稳定自转的临界条件和转速的概念，难度较大，可作为能力提升练习题。

【答案】B

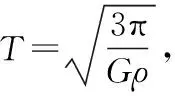
【设计意图】当匀质球形自转天体处于稳定自转的临界状态时，地表各处的重力加速度呈现特殊的分布，对于感兴趣的学生，可用该题拓展学生思维能力和学习兴趣。

【解题指南】当天体处于稳定自转的临界状态时，如图1所示，对万有引力F正交分解后，可以证明任意纬度处星球表面的物体所需的自转向心力，恰好等于万有引力平行于赤道面指向地轴的分力Fcosθ，而另一分力即重力恰好等于Fsinθ，且方向垂直于赤道面，考虑极地处有F=mg0，代入后可得地表各处的加速度g随纬度θ的分布。

图1

【答案】g=g0sinθ，方向均垂直的指向赤道面。

四、结束语