3种附属管排布方式对主管路水动力特性的影响

黄 技，王成彦，巫凯旋，陶韵如，赵远溥，尹 辉

3种附属管排布方式对主管路水动力特性的影响

黄 技1，王成彦2，巫凯旋2，陶韵如1，赵远溥2，尹 辉2

（1. 广东海洋大学海洋工程学院 / 2. 广东海洋大学海运学院，广东 湛江 524005）

【目的】研究均匀流多管束干涉流动下圆柱受迫振动的水动力特性。【方法】基于SST模型，在亚临界雷诺数下（=1×105）对多管束共振强迫的涡激振动问题进行二维数值模拟，比较与分析三种典型附属管排布方式对主管路流体动力学特征的影响。【结果与结论】采用模型3下的附属管排布方式可在较大范围的振幅比下（A/0.1 ～ 0.8）有效改善主管路水动力特性：1) 有效降低主管路上平均升力系数的幅值；2) 抑制在单管路系统中出现的脉动升力系数突变衰减。同时，由于多管束对流动产生干涉效应，主管路上表现的尾迹涡度随着振动幅度的增大而呈现出不同的模式。此外，功率谱密度分析发现，多管束系统相较于单圆柱系统，在频率比为1时，模型2与模型3的共振“锁定”状态得到改善。

涡激振动；受迫振动；水动力特性改善；多管束排布方式；重叠网格

随着海洋油气资源开采逐步走向深海海域，诸如海洋平台支撑柱和海底管线在波流联合作用下产生的涡激振动（Vortex induced vibration, VIV）问题受到工业界和学术界的高度关注[1-2]。为将复杂的流固耦合问题简化，常将海洋立管视为简单刚性柱体，且将刚体六自由度简化为一或两个自由度。对简单刚性柱体的涡激振动研究可分自激振动与受迫振动两类，前者更多考察质量比、结构阻尼因子以及约化速度对结构振幅的影响，而后者更加侧重研究不同振幅、频率比下结构的流体力变化情况以及流体与结构间能量转移。潘志远[3]对自激振动与受迫振动内在联系的研究发现，海洋立管在洋流作用下产生涡激振动，对于整个立管而言，是自激产生的；但若考虑每一节可视为刚体的分段，则这种振动却是受迫振动。目前国内外对圆柱受迫振动已进行大量研究。Williamson等[4]的实验（= 400）得出，在一定振幅与频率范围内对应的不同涡街脱落模式有“2S”“2P”“P+S”以及非典型尾流模式。相较于低雷诺数下进行的研究，高雷诺数下得到的结果更贴近工程实际应用。樊娟娟等[5]对高雷诺数下（= 105、2.5×105）大振幅比圆柱受迫振动进行数值模拟，得到升力系数及涡街泄放规律。喻晨欣等[6]采用高分辨率TVD-FVM方法对二维圆柱受迫振动问题（= 104）进行求解，划分出激振区的无量纲频率范围。朱永健等[7]对亚临界区（= 105）下受迫振动圆柱所表现出的流体力不连续现象进行研究，分析尾迹模式对动力响应内在的关联性。对单圆柱自激振动的研究发现，在质量比较小的情况下，圆柱自激横向最大振幅比约为0.6[8-9]，而朱永健等[7]对受迫振动圆柱的研究结果表明，当振幅比约为0.6时，圆柱的升力系数发生突变。海洋立管为典型的低质量比柱体结构，最大振幅下的升力系数突变将不利于海洋结构物的安全运行，因此，对该系统进行深入研究具有工程实际意义。

为预防和减少涡激振动对结构物的损害，控制方法可分为主动控制法和被动控制法两类。主动控制法需要外部能量输入，如在立管外围添加旋转叶片、对管路表面加热等，该方法经济性较差。被动控制法无需外界能量的摄入，如添加整流罩，螺旋列板和分离盘等，但存在易腐蚀、减升增阻现象以及不能适应来流方向的变化等问题[10]。

在工程实际中，除主管路外，还需一些附属管线，如液压管线、泥浆增压管线等。附属管一方面为工程实际所必须，另一方面可提高系统的力学性能。目前，对于多圆柱系统涡激振动研究较少报道，已有研究多停留在双圆柱并列、串列分布范畴，且多为低雷诺数下的研究[11-13]。然而，在实际工程中，水下立管处于高雷诺数流动区域，且附属管线排布方式对多管束系统研究尚缺少完整体系，基于此，笔者团队对亚临界高雷诺数下错列、不等直径的多圆柱振动耦合系统做进一步研究。

本研究利用UDF动态链接库进行二次开发，结合重叠网格技术，比较= 105下三种典型附属管排布方式下受迫振动圆柱的水动力特性，以期对深海立管等结构物的设计制造提供技术支持。

1 理论方程与数值模型

1.1 控制方程

本研究采用SST湍流模型求解不可压缩的N-S方程。连续性和动量方程可表示为

SST模型由Menter[14]最先提出，在预测近壁区绕流和旋流方面有优势，并具有较高精度和可信度。其湍动能与比耗散率的输运方程为

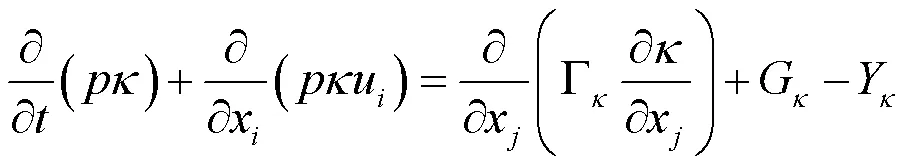
本研究采用有限体积法对控制方程进行离散，动量方程中的压力-速度耦合项采用Coupled算法，对流项采用二阶格式离散以达到较高计算精度，瞬态项使用一阶隐式格式以满足重叠网格计算需求。

1.2 受迫振动计算模型

本研究采用Fluent软件中的重叠网格（Overset Mesh）模拟圆柱的横向振动，同时结构性网格保证了计算网格的质量。均匀流雷诺数105，平行于来流方向的坐标轴设为，垂直于来流方向设为，瞬时圆柱横向位移η表达式为

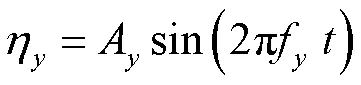
式（5）中，A为圆柱横向振幅，f为横向强迫振动频率，为时间。故，圆柱运动速度可表示为

式（6）中，f为圆柱震动频率。

单位圆柱长度上的流向力F和横向力F分别为

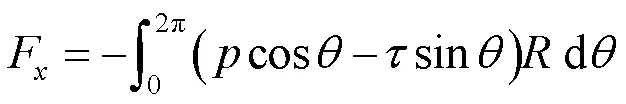
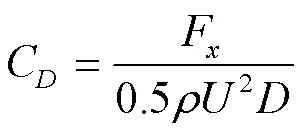
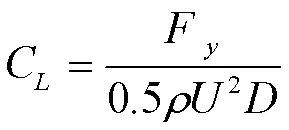
F、F分别为作用于单位长度圆柱上的阻力和升力，表示流体密度，为流体速度，为圆柱直径。

本研究选取的频率比f/f= 1.0（其中，f为横向强迫振动频率，f为流经固定圆柱时的漩涡脱落频率），振幅比A/范围为0.1 ～ 1.0。

2 计算模型及算例验证

2.1 计算域及边界条件

本研究所选取的计算域见图1，大小为24× 45，圆柱直径设置为1 m。

附属管与主管道之间的排布方式难以穷尽，为简化研究，本研究选取三种典型的排布方式[10]（图2）：模型1为位于上游的串列附属管和错列附属管，模型2为位于下游的串列附属管和错列附属管，模型3为对称分布于下游的错列附属管。附属管直径= 0.25，主管路与附属管间的间距= 0.8，错列附属管与流向的夹角设置为45°。

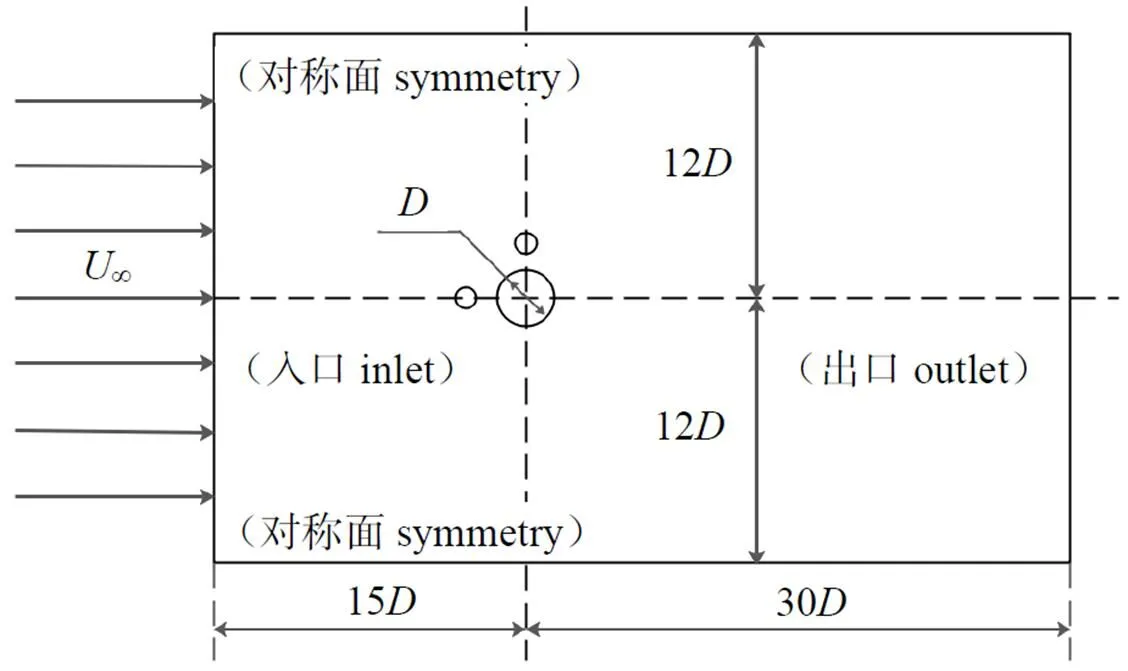
图1 计算域示意

图2 管路排布方式模型

使用分块划分的方法对圆柱及尾流区域网格进行局部加密（图3）。在圆柱周围设置重叠网格，重叠区域为直径为1.75的圆。为验证网格无关性，分别计算网格总数为52万、73万、109万时的结果，针对升力系数最大值Cmax和升力系数均方根值Crms进行对比（表1）。为保证计算精度和计算效率，本研究最终选择73万网格进行计算。黏性底层区域通常用距离无量纲参数+表示，陈懋章将+= 5划为黏性底层和过渡层的分界点[15]，本研究保持第一层网格高度+≈ 1，范围在1 ～ 5之间，符合理论上对黏性底层的界定。

本研究设置边界条件：进口为速度入口，出口为压力出口，上下边界为对称边界，圆柱表面为无滑移壁面，重叠网格边界设置为嵌套边界条件。为提高计算效率和精度，本研究首先进行300步稳态模拟，再进行瞬态计算，时间步长设置为0.01 s。

图3 网格划分示意

表1 网格无关性分析

2.2 算例验证

为验证选取网格和计算模型的准确性，本研究（= 1×105）与朱永健等[7]（= 1×105）、盛磊祥[16]（= 2.5×105）、Gopalkrishnan[17]（= 1×104）的实验或数值结果进行对比验证（图4）。本研究与朱永健等[7]的结果吻合较好，且与其他学者计算结果所表现的趋势保持一致，验证了本研究所选湍流模型求解亚临界雷诺数下圆柱受迫振动问题的准确性。当雷诺数较小时结果相差较大，体现出雷诺数对流场的影响作用，符合实际情况。为深入了解升力系数曲线随时间的变化情况，对应f / f= 0.7、1.0、1.3的工况下的升力系数历时曲线见图5(a-c)。升力系数曲线表现为平滑的正弦曲线，并未出现“拍频”特征，这说明漩涡发放频率等于圆柱振动频率。

图4 CLmax随频率比的变化曲线

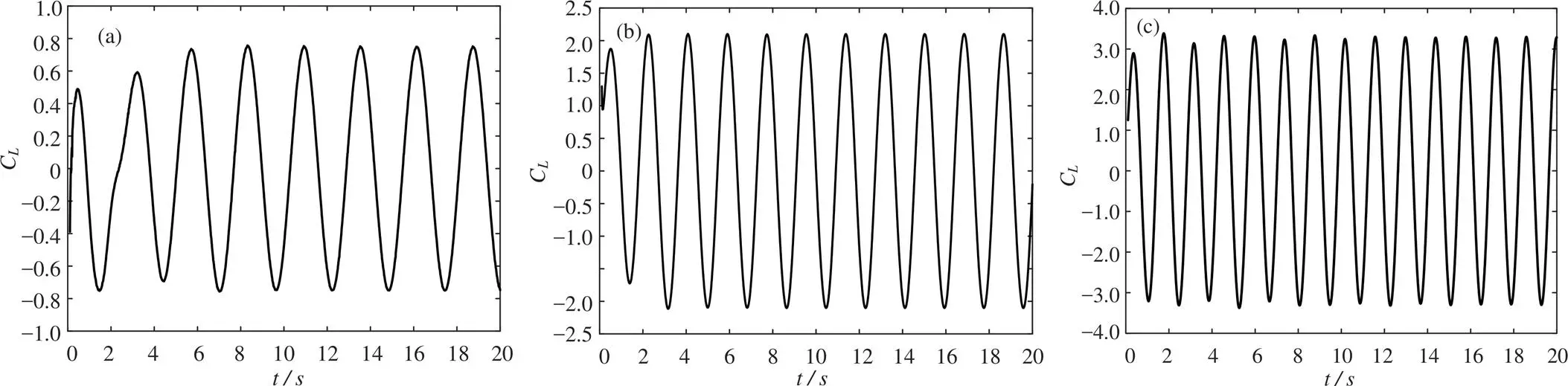
(a) fy / fs = 0.7, Ay / D = 0.25; (b) fy / fs = 1.0, Ay / D = 0.25; (c) fy / fs = 1.3, Ay / D = 0.25

3 结果与分析

3.1 对脉动升力系数的影响

图6为在= 105，强迫共振（f/ f=1.0）下，脉动升力系数最大值Cmax随振幅比A/ D的变化规律。

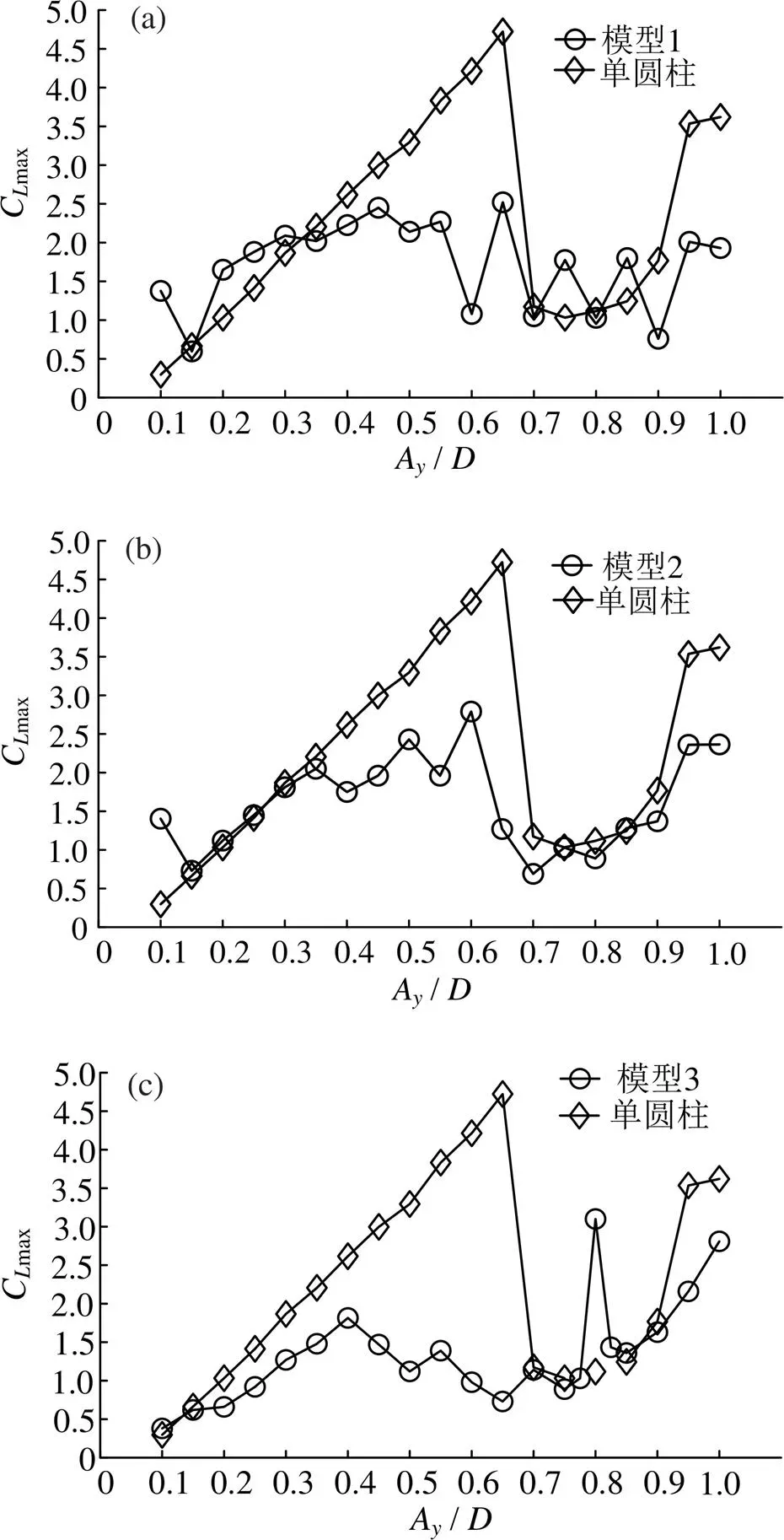
图6 脉动升力系数与振幅的关系

当为单圆柱受迫振动时，在A/ D < 0.65时，脉动升力系数最大值Cmax呈现单调递增的趋势，线性度保持较好。而在A/ D = 0.65时，升力系数Cmax表现为跳跃式下降，降幅达75.15%，随后保持较小值且变化较小。当A/ D = 0.85时，单圆柱系统升力系数Cmax再次呈现跃升，幅度达200%。在单圆柱系统中，结构的流体力表现出强非线性和突变性。

模型1下的多管束系统最大限制脉动升力系数Cmax幅值可达74.37%，但在局部区间下表现出了震荡性（图6(a)）。当振幅较大时表现出的升力系数变化复杂，变化曲线连续性较差等现象与朱永建等[7]在研究单圆柱共振问题时所表现出的现象相近。同时，本研究发现，在模型1下，升力系数幅值变化情况较单圆柱震荡倾向更为显著，这表现出结构-流体能量传递关系发生的交替转换，Cmax跳跃下降即表明能量传递的突然减少，反之则表明能量传递的突然增多。结构在发生横向受迫振动时的瞬时位移为()，在每一个振动周期内，流体向结构传递的机械能可写成如下无量纲形式：

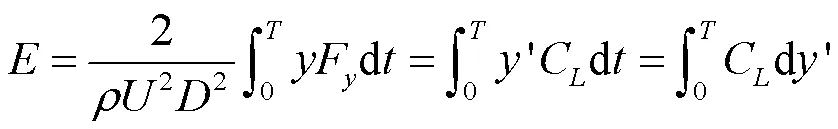
式中，为圆柱受迫振动的周期，′() =() /为圆柱瞬时位移的无量纲表达式。

也称为流体-结构能量传递系数，为正值则流体对结构做功，为负值则结构对流体做功，并且Blackburn等[18]指出，单根圆柱体受迫振动时，尾涡生成和圆柱体运动之间的相位关系变化伴随着符号的变化。

从公式(11)可看出，与升力系数C之间的关系：流体与结构之间能量传递、做功情况的反复突变，将导致升力系数产生相应的变化。这是在振幅A / D在0.60 ～ 0.95间升力系数产生震荡的原因。

模型2下的多管束系统所表现出的升力系数最大值Cmax随A/的变化规律（图6(b)），其与单圆柱系统相近，变化趋势上也呈现出两次跃迁：A/= 0.65时突降，A/= 0.95时跃升，且A/在0.1 ～ 0.6间基本保持单调递增的趋势。

模型3下的多管束系统升力系数最大值Cmax的变化情况（图6(c)），对比前两种模型与单圆柱系统，其升力系数最大值Cmax连续性较好，最大控制升力系数幅值比例达84.54%。当A/= 0.80时，升力系数有较大突变。本研究对振幅比为0.80附近的数据进行加密，通过对比升力历时曲线（图7）发现：流场刚开始发展时，历时曲线重合度较高，故可排除数值振荡的情况。当流场时间大于100 s，振幅比为0.80时，圆柱的升力系数变化呈规则的周期性震荡，与单圆柱绕流情况类似[19]，而相近数据点周期性不明显，可推测当振幅比为0.80时，由于受到下游圆柱漩涡脱落影响产生共振，因此造成升力系数突然跃升。

图7 振幅比在0.80附近时的升力系数时程曲线对比

3.2 对尾迹变化的影响

为研究升力系数突变与尾迹变化的内在联系，本研究选取具有代表性时刻的圆柱尾流云图进行研究：1）升力系数幅值反复震荡；2）升力系数突变；3）升力系数达到极值。本研究发现，尾迹模式与升力系数变化具有相关关系：当尾迹较为紊乱、无序且分散时，往往圆柱的升力系数幅值较低。且从其时程曲线来看并不构成典型的类正弦波动周期，而是无规律、非周期的，这也是圆柱尾流为非典型模式的原因。

图8(a-h)为模型1分别对应A/= 0.55、0.60、0.65、0.70、0.75、0.80、0.85、0.90时所表现出的圆柱尾迹涡量图。图8(a)表现为类“P+S”模式：随着流场的发展，管束系统后泄放的漩涡先由多个较为狭长的涡相互吸引组合为3个，进而合并为2个，即呈现出“2S”型，并且涡的形状为较为规则的圆形。图8(b)为A/= 0.60时情况，此时的升力系数发生突降，管束系统后的涡量表现为细小漩涡先聚合为两个较为规则的圆形，而后又发生耗散并不断破裂。随后，涡量图（图8(c-h)）表现为典型涡街的反复建立而又被破坏，升力系数幅值表现为反复震荡。不同振幅下，圆柱尾流呈现出不同模式，反映了尾涡结构伴随着流体-结构能量传递系数的变化，这与3.1节所述一致。

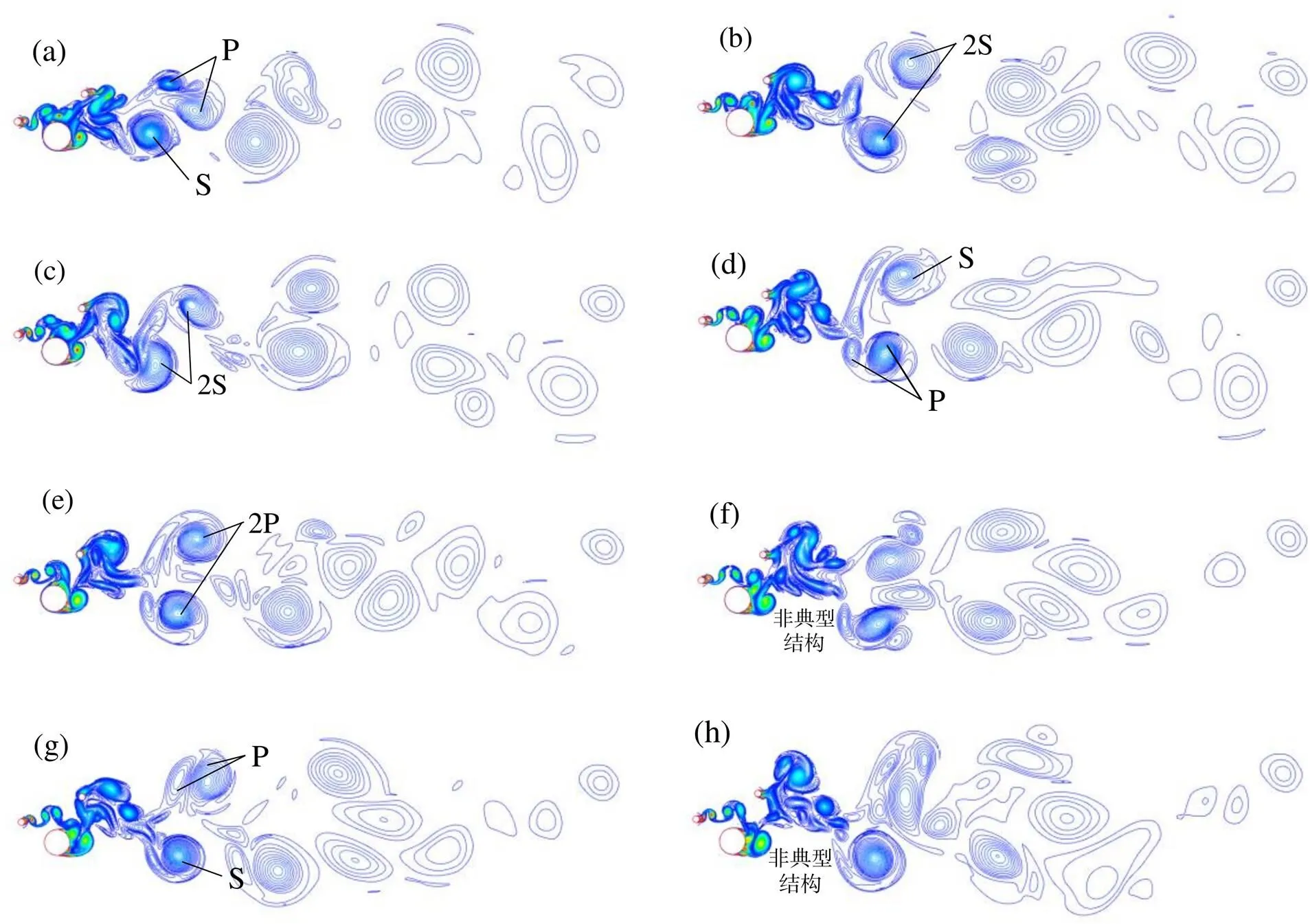
(a) Ay / D = 0.55; (b) Ay / D = 0.60; (c) Ay / D = 0.65; (d) Ay / D = 0.70;(e) Ay / D = 0.75; (f) Ay / D = 0.80; (g) Ay / D = 0.85; (h) Ay / D = 0.90

图9(a-d)为模型2分别对应A/= 0.55、0.60、0.65、0.70时的尾迹涡量图。图9(a)表现为“2P”模式，随着振幅比继续加大，涡量开始集中，升力系数曲线表现为达到极大值。当振幅比达到0.65时，升力系数突降，此时漩涡已经较为分散（图9(c)）。而当振幅比继续增大，漩涡已变得十分破碎，反映在升力系数幅值上为抵达最小值（图9(d)）。A/= 0.55、0.65时，模型2与单圆柱系统一样，在涡流尾迹均出现“2P”模式（图9(a、c)）。通过该组的试验发现，即使流场当中的结构发生变化，但脱落的涡街结构相似时，其受力特性也具有关联性。

(a) Ay / D = 0.55; (b) Ay / D = 0.60; (c) Ay / D = 0.65; (d) Ay / D = 0.70

图10(a-d)为模型3分别对应A/= 0.20、0.40、0.75、0.80时的尾迹涡量图。由于下游两附属管对流动干涉影响较大，模型3各尾迹图大多并未表现出典型的尾流模式，即振幅比A/ D较小时，系统产生许多较小的漩涡，但这些漩涡并不相互聚合。当A/ D = 0.40时，升力系数幅值达到极大值点，涡量图发生明显的变化，漩涡发生相互聚合，涡量图呈现为“2S”模式。当振幅比为0.80时，升力系数幅值发生突变，涡量图上表现为漩涡较为集中，且涡量尾迹图表现出非典型模式，这与之前模型2所观测到的现象相吻合。

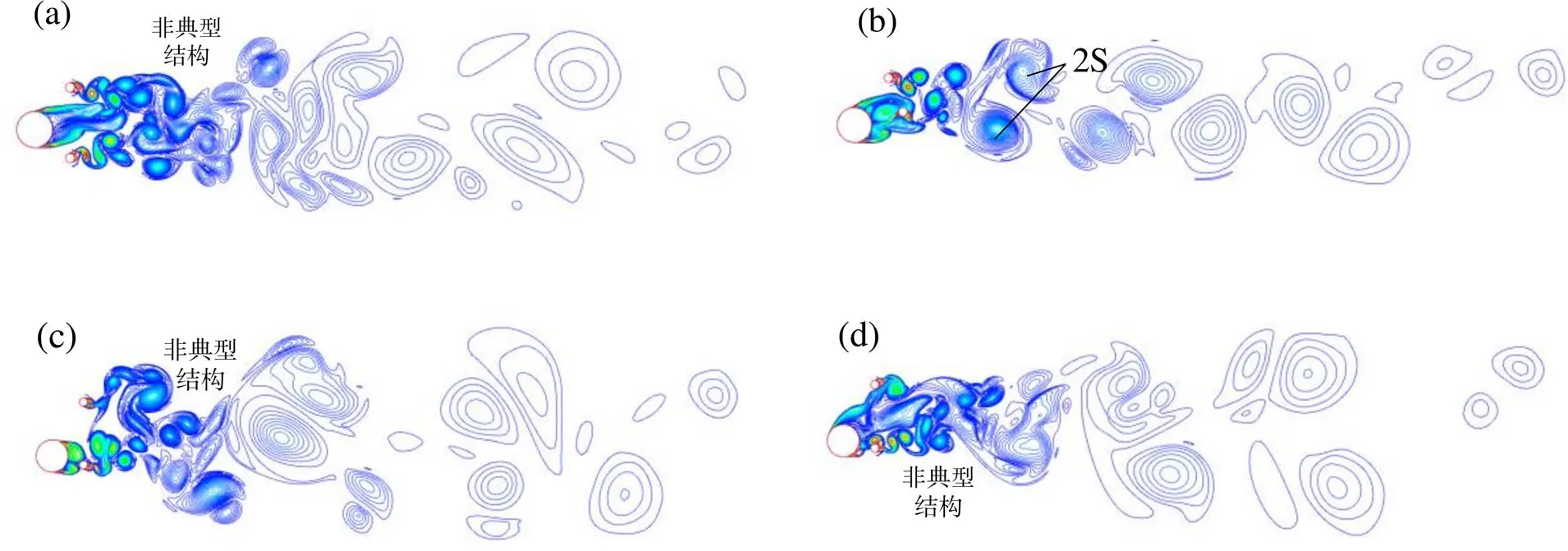
(a) Ay /D = 0.20; (b) Ay /D = 0.40; (c) Ay /D = 0.75; (d) Ay /D = 0.80

综上可知，涡街所呈现出的模式与升力系数幅值有着密切的内在联系，当圆柱系统的尾流表现为典型的“2S”“2P”以及“P+S”时，升力系数幅值往往较为稳定，且随着振动幅度的增加表现出一定的单调性。而当圆柱系统的尾迹涡街表现为非典型结构时，也可分为两种情况：1）涡街较为集中且细密，此时升力系数幅值往往较大；2）涡街结构较为破碎，表现得十分分散，此时对应的升力系数幅值往往较小，且从升力系数历时曲线来看往往并没有规律性和周期性。

3.3 对压力系数分布的影响

为进一步研究模型3在振幅比A/= 0.80附近表现出的升力系数幅值的跃变，对A/= 0.75、0.80、0.85圆柱表面时均压力系数分布进行分析（图11），其中= 0°为圆柱前缘处驻点。由于圆柱横向震荡且附近存在附属物，故圆柱表面上下压力系数分布并不对称。同时，可以看出在A/= 0.75、0.85时，时均压力系数分布虽然在具体数值上存在差异，但是二者有着相似的变化规律，表现为二者有相近的升力系数幅值。而A/= 0.80时，压力系数分布则有较大的差别：0° << 120°时三者变化趋势相近，但振幅比为0.80时的压力系数数值更大；当> 120°时，振幅比为0.80时的压力系数变化规律为略有下降后不断增加，直至到达最大值；而A/= 0.75、0.85时，压力系数基本保持为负值，呈现先快速下降再上升，继而持平后快速上升的特征。

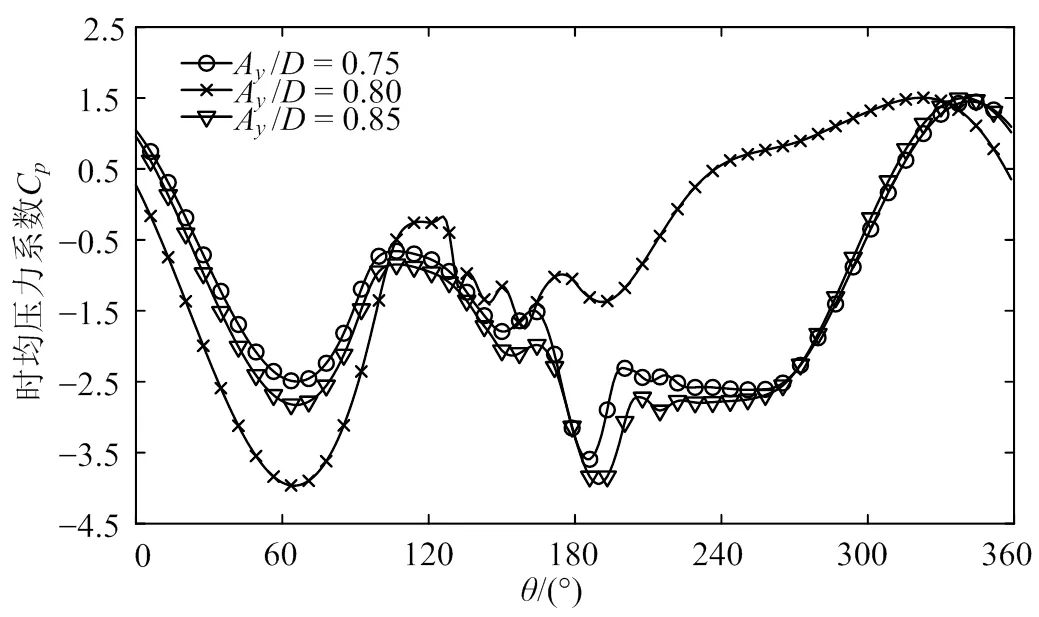
图11 模型3不同振幅比下的时均压力系数曲线

3.4 对能量频谱密度的影响

本研究通过对3种模型下的升力系数时程曲线进行快速傅里叶变换（FFT）得到功率谱密度（Power Spectral Density，PSD，图12）。由图12(a-c)可见，在A/= 0.70时，斯特鲁哈数（Strouhaul Number,S）具有2个峰值，这说明3种模型在此振幅比下圆柱漩涡脱落不仅受到圆柱震动频率f的影响，还受到固定圆柱泄涡频率f的影响。由图12(d-f )可见，当A/= 0.95时，模型2与模型3的PSD图谱出现2个峰值，而模型1并没有出现，这说明在模型1在振幅比为0.95时的共振“锁定”效应更为强烈。除上述两个特殊振幅比外，PSD图谱均保持单峰值，表现出共振“锁定”现象。

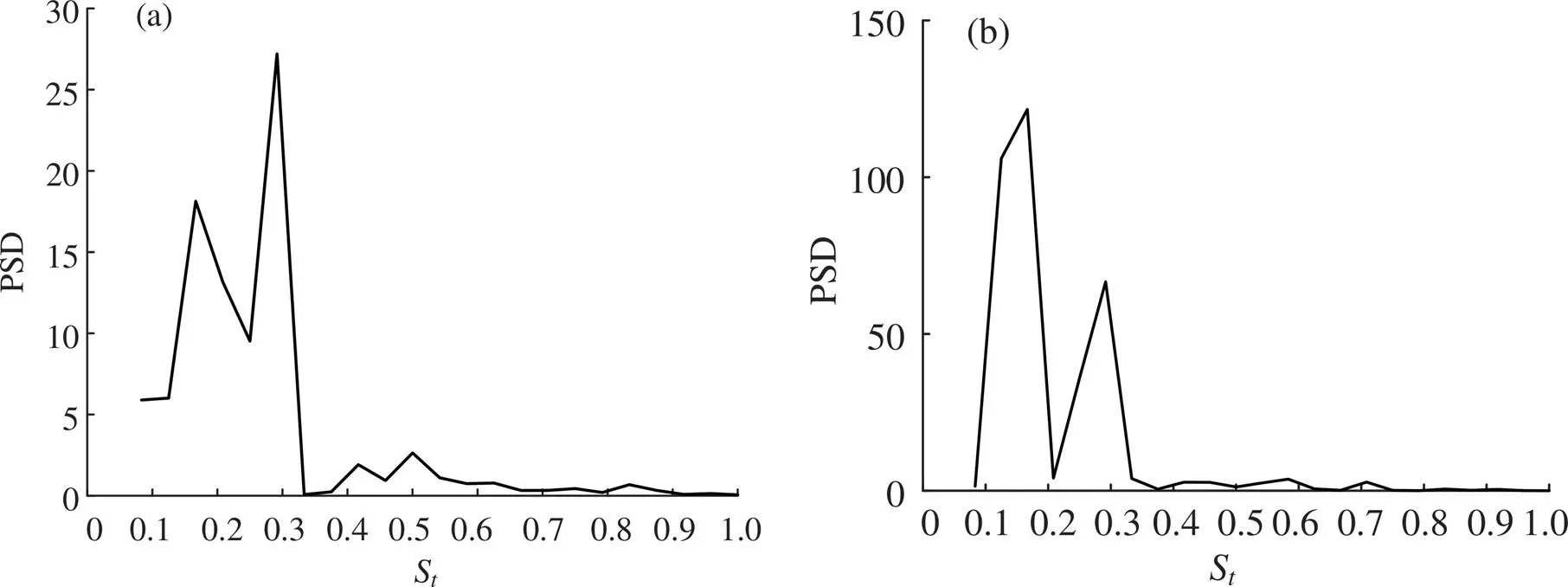
(a) Ay / D = 0.70, 模型1; (b) Ay / D = 0.70, 模型2

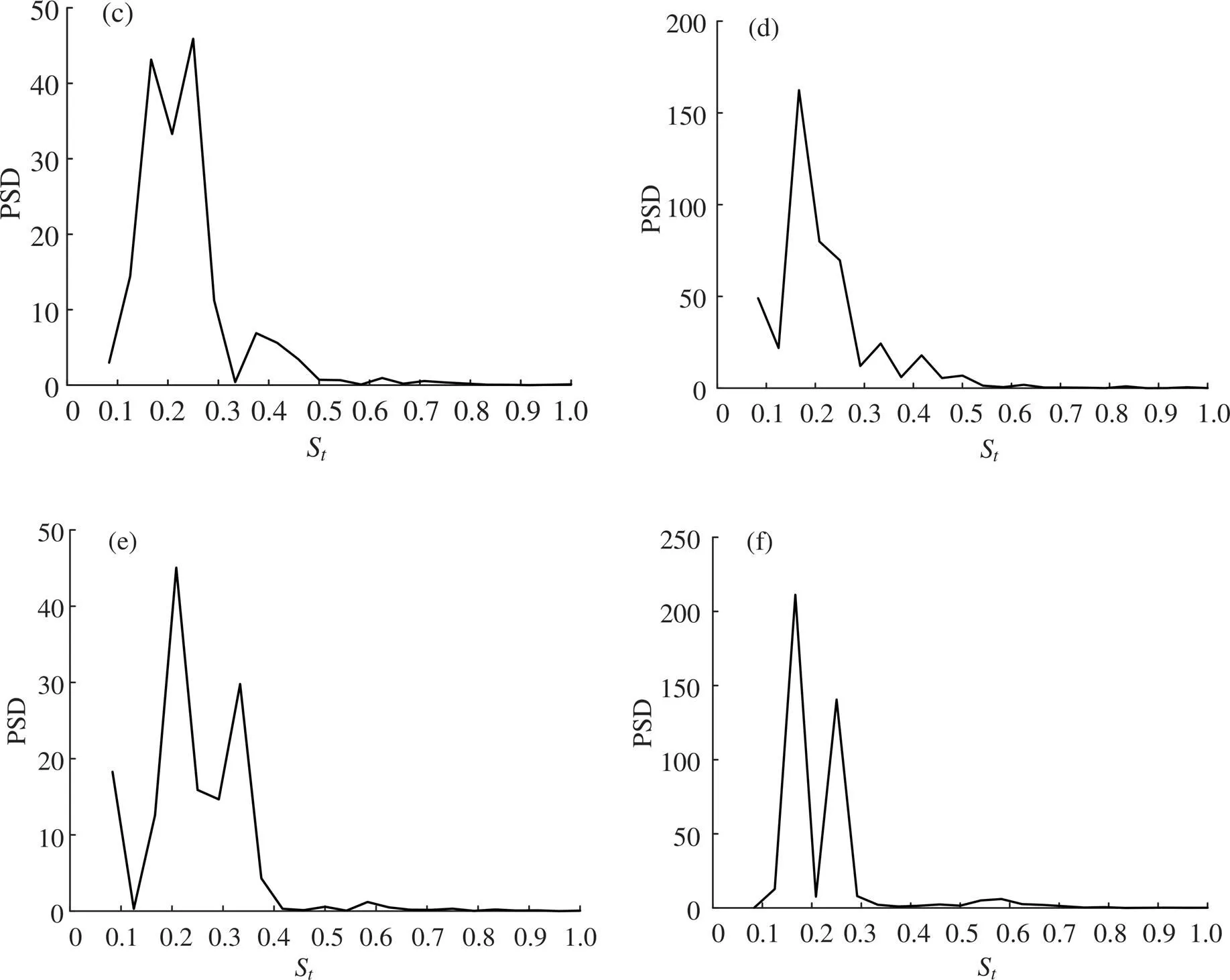
(c) Ay / D = 0.70, 模型3; (d) Ay / D = 0.95, 模型1; (e) Ay / D = 0.95, 模型2; (f) Ay / D = 0.95, 模型3

4 结论

本研究基于SST模型的数值模拟方法对均匀流多管束干涉流动下圆柱受迫振动的水动力特性进行探讨，重点分析在主管路与附属管间距比= 0.8及附属管直径= 0.25的情况下，三种典型附属管排布方式对主管路流体力的影响以及升力系数幅值与涡量图之间的内在联系，得到如下结论：

1）数值模拟结果表明，选用合理的附属管排布方式可限制圆柱的最大升力系数幅值，且可有效改善圆柱的流体力突变情况。在振幅比小于0.80时，选用本研究中的模型3可有效改善多管束系统的受力情况。

2）多管束系统的尾迹涡量图与其脉动升力系数变化情况有着密切的内在联系。由于附属管的流动干涉作用，系统尾迹出现了典型的涡街脱落模式，如“2S”“2P”及“P+S”模式，且本研究通过联系升力系数曲线图与涡量图发现：当形成的尾涡为非典型模式且集中时，其升力系数幅值往往较大；而当尾涡无序、分散甚至破碎时，其升力系数往往幅值较小。

3）PSD图谱分析发现，在振幅比为0.70与0.95时，3种模型均表现为未“锁定”状态；在振幅比为0.95时，模型2与模型3表现为未“锁定”状态，而模型1表现为“锁定”状态。这表明，相较于单圆柱系统，在频率比为1时，模型2与模型3的共振“锁定”状态得到改善，对深海立管等结构物的设计制造具有一定的指导意义。

[1] 赵静, 吕林, 董国海, 等. 亚临界雷诺数下圆柱受迫振动的数值研究[J]. 计算力学学报, 2012, 29(1): 74-80.

[2] 王志东, 周林慧. 均匀流中横向振荡圆柱绕流场的数值分析[J]. 水动力学研究与进展(A辑), 2005, 20(2): 146-151.

[3] 潘志远. 海洋立管涡激振动机理与预报方法研究[D].上海: 上海交通大学, 2006．

[4] WILLIAMSON C H K, ROSHKO A.formation in the wake of an oscillating cylinder[J]. Journal of Fluids and Structures, 1988, 2(4): 355-381.

[5] 樊娟娟, 唐友刚, 张若瑜, 等. 高雷诺数下圆柱绕流与大振幅比受迫振动的数值模拟[J]. 水动力学研究与进展A辑, 2012, 27(1): 24-32.

[6] 喻晨欣, 王嘉松, 郑瀚旭. 高分辨率TVD-FVM方法求解二维圆柱受迫振动问题[J]. 水动力学研究与进展(A辑), 2018, 33(5): 593-600.

[7] 朱永健, 宗智. 定常流中横向振动圆柱的升力突变现象研究[J]. 水动力学研究与进展(A辑), 2020, 35(5): 592-600.

[8] AHN H T, KALLINDERIS Y. Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes[J]. Journal of Computational Physics, 2006, 219(2): 671-696.

[9] BORAZJANI I, SOTIROPOULOS F.-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region[J]. Journal of Fluid Mechanics, 2009, 621: 321-364.

[10] 吴文波. 海洋结构中多圆柱流动干涉与涡激振动特征研究[D]. 上海: 上海交通大学, 2017.

[11] 涂佳黄, 杨枝龙, 邓旭辉, 等. 上游静止柱体对圆柱体结构尾激振动的影响[J]. 船舶力学, 2020, 24(2): 179-190.

[12] 姚熊亮, 陈起富, 徐文景. 均匀流场串列圆柱涡激振动特性的实验研究[J]. 振动工程学报, 1994(1): 17-22.

[13] 张晓娜, 及春宁, 陈威霖, 等. 正三角形排列刚性耦合三圆柱涡激振动特性及尾涡模式[J]. 振动与冲击, 2021, 40(12): 132-142.

[14] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[15] 陈懋章. 粘性流体动力学基础[M]. 北京: 高等教育出版社, 2006.

[16] 盛磊祥. 海洋管状结构涡激振动流体动力学分析[D]. 青岛: 中国石油大学, 2008.

[17] GOPALKRISHNAN R. Vortex-induced forces on oscilla­ting bluff cylinders[D]. Cambridge, MA, USA: Massachusetts Institute of Technology, 1993.

[18] BLACKBURN H M, HENDERSON R D. A study of two-dimensional flow past an oscillating cylinder[J]. Journal of Fluid Mechanics, 1999, 385: 255-286.

[19] 黄技, 吕鸿冠, 林灿彬, 等. 基于fluent的不同雷诺系数下二元圆柱绕流的研究[J]. 广东海洋大学学报, 2015, 35(4): 81-86.

Influence of Three Arrangement Modes of Auxiliary Pipes on Hydrodynamic Characteristics of Main Line

HUANG Ji1，WANG Cheng-yan2，WU Kai-xuan2，TAO Yun-ru1，ZHAO Yuan-pu2，YIN Hui2

( 1./ 2.,,524005,)

【Objective】The study is to investigate the hydrodynamic characteristics of cylinder subjected to forced vibration under the interference flow of multiple bundles with uniform flow. 【Method】Based on SSTmodel, under subcritical Reynolds number (= 1×105), a two-dimensional numerical simulation of the vortex-induced vibration problem of multi-tube bundle resonance was carried out, and the influence of three typical auxiliary tube arrangement methods on the hydrodynamic characteristics of the main pipeline were compared 【Result and Conclusion】The arrangement of auxiliary pipes under Model 3 can effectively improve the hydrodynamic characteristics of the main line at a wide range of amplitude ratios (A/0.1 - 0.8 ): 1) Effectively reduce the average lift coefficient of the main line; 2) Suppress the sudden attenuation of the pulsating lift coefficient in the single-piping system. Meanwhile, due to the interference effect of the multi-tube bundle on the flow, the wake vorticity of the main pipe shows different patterns with the increase of vibration amplitude. In addition, Power Spectral Density analysis shows that the resonance “lock-in” state of Model 2 and Model 3 of the multi-bundle system is improved when the frequency ratio is 1, compared with the single-cylinder system.

vortex induced vibration; forced oscillation; improved hydrodynamic characteristics; multi-tube bundle arrangement; overset mesh

O351.3

A

1673-9159（2022）01-0127-10

10.3969/j.issn.1673-9159.2022.01.017

黄技，王成彦，巫凯旋，等. 3种附属管排布方式对主管路水动力特性的影响[J]. 广东海洋大学学报，2022，42（1）：127-136.

2021-07-24

广东海洋大学大学生创新创业训练计划项目（CXXL2021302）；2020年广东省促进经济高质量发展专项（军民融合发展）；湛江市非资助科技攻关专题（2020B01416）

黄技（1988―），男，硕士，讲师，研究方向为海洋结构物水动力性能。E-mail: huangji@gdou.edu.cn