基于APDL语言的牛头刨床机构运动学分析

肖 超，李 伟，邵 腾，丛日平

(山西航天清华装备有限责任公司 技术中心，山西 长治 046000)

0 引言

随着计算机科学技术应用领域的不断拓展，虚拟样机仿真技术在工程机械开发中得到了广泛的应用。文献[1-3]都通过虚拟样机对牛头刨床的运动学和动力学进行了仿真分析并进行了结构优化设计。

分析发现，现有研究多数是在设计方案确定后，基于比较完善的三维模型进行虚拟样机仿真研究。而在方案设计前期，如何能够快速获得不同方案的运动学、动力学特性，进行方案择优则成为难点。为此，本文基于ADPL语言的机构仿真分析方法，以牛头刨床为例进行机构运动学分析。并通过与理论结果的对比分析，验证该方法的可行性，对类似的机构仿真研究具有一定的理论指导意义。

1 基于APDL语言的参数化分析流程

参数化设计语言APDL(Parametric Design Language)使研发人员对结构设计或分析具有绝对控制权，通过修改尺寸、材料、载荷等参数，可以快速实现具有相同结构的不同系列产品的刚度分析、谐响应分析、结构优化设计等[4]。基于APDL的参数化分析流程如图1所示。

图1 基于APDL的参数化分析流程

针对工程实际问题，通过提取事物结构特征及拓扑约束关系，将其转化为用APDL语言表达的程序，在程序运行和调试的基础上，求得问题的结果。

2 牛头刨床参数化建模

2.1 基本结构及参数

常见的牛头刨床大多采用如图2所示的六杆机构传动。其中，曲柄1、导杆3、机架4及滑块组成摆动导杆机构，为便于与文献[5]中的理论计算结果进行对比分析，假设杆件1在初始状态处于水平位置。

确定输入参数(默认长度单位为mm)，用APDL表达为：

r=100 !杆件1的回转半径

h1=350 !点O与点B之间的垂直距离

h2=350 !点A与点C之间的垂直距离

h3=250 !点C与点D之间的垂直距离

a=200 !点D与点F、点G之间的水平距离

1-曲柄；2，5-滑块；3-导杆；4-机架；6-推杆；7，8-连杆

2.2 参数化建模

根据牛头刨床的机构特点，用定义的输入参数将每个关键点在坐标系中的位置用APDL语言表示出来，再选择相应的单元类型，建立参数化模型。用APDL表达为：

/prep7 !进入前处理模块

!定义关键点位置

n,1 !定义点B的位置

n,2,0,h1 !定义点O的位置

n,3,r,h1 !定义点A的位置

n,4,2*r,h1+h2 !定义点C的位置

n,5,2*r,h-h3-100 !定义点E的位置

n,6,2*r,h !定义点D的位置

n,7,2*r-a,h !定义点F的位置

n,8,2*r+a,h !定义点G的位置

!定义单元类型

et,1,mpc184,1,1 !MPC184，刚性梁单元

et,2,mpc184,3 !MPC184，滑块连接单元

et,3,mpc184,6 !MPC184，销轴连接单元

et,4,mpc184,10 !MPC184，平移连接单元

!创建MPC184刚性梁单元

type,1

e,1,4 !定义导杆3

e,2,3 !定义曲柄1

e,5,6 !定义推杆6

e,6,7 !定义连杆7

e,6,8 !定义连杆8

!创建MPC184销轴连接单元

local,12,,,,,,,90

sectype,1,joint,revo

secjoint,lsys,12

type,3

secnum,1

e,1

!创建MPC184滑块单元

type,2

e,3,1,4 !创建滑块2

e,4,5,6 !创建滑块5

!创建MPC184平移连接单元

local,13

sectype,2,joint,pris

secjoint,lsys,13

type,4

secnum,2

e,7 !创建杆7及杆8的平移单元

由以上APDL语言建立的牛头刨床参数化模型如图3所示。

图3 基于APDL建立的牛头刨床参数化模型

2.3 施加边界条件

在点O处施加位移边界条件。约束和荷载用APDL表示为：

d,2,ux,,,,,uy,uz,rotx,roty !约束点O位移

d,2,rotz,2*acos(-1) !在点O处施加位移驱动

2.4 求解及结果输出

由于篇幅限制，本文只对点D的速度、加速度以及导杆3的角速度、角加速度进行求解分析。用APDL表达为：

!求解

/solu

time,1.2 !在1.2s内曲柄1旋转360°

nlgeom,on

outres,all,all

nsubst,100,,50

solve

!结果输出

/post26

nsol,2,7,u,x !点D的位移曲线

deriv,3,2 !点D的速度曲线

plvar,3 !绘制点D的速度曲线

deriv,4,3 !点D的加速度曲线

plvar,4 !绘制点D的加速度曲线

nsol,5,1,rot,z

deriv,6,5,,,,,,57.29577 !导杆3的角速度

plvar,6 !绘制导杆3的角速度曲线

deriv,7,6 !导杆3的角加速度

plvar,7 !绘制导杆3的角加速度曲线

由此，可以得到点D的速度曲线(见图4)和加速度曲线(见图5)以及导杆3的角速度曲线(见图6)和角加速度曲线(见图7)。

图4 点D的速度曲线 图5 点D的加速度曲线 图6 导杆3的角速度曲线

2.5 仿真结果验证

将导杆3的角速度、角加速度曲线与文献[5]中的理论计算结果(如图8、图9所示)对比分析可知，基于APDL语言得到的虚拟样机仿真结果与理论分析结果完全一致，证明了该方法求解结果的正确性。

2.6 系列机构求解

通过修改2.1节中的输入参数，可以快速获得不同结构尺寸的牛头刨床的运动学仿真结果，这里不再一一赘述。

3 结语

本文基于APDL语言建立了牛头刨床机构的参数化模型并进行了运动学仿真，通过与理论计算结果的对比分析，证明了该方法的正确性，从而为用户摆脱繁琐的理论计算，直观、快速地获得机构运动学分析结果提供了一种新思路。

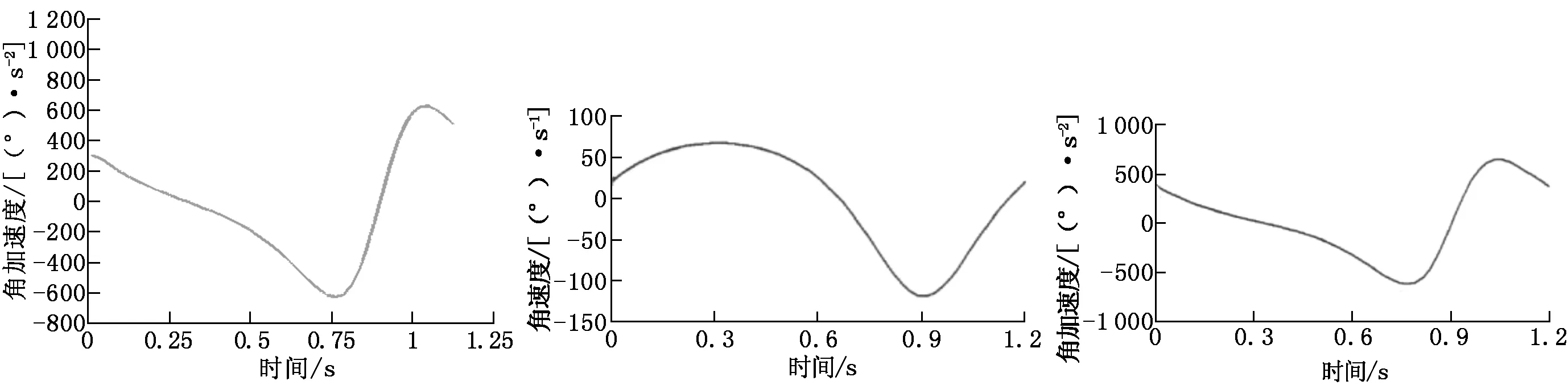
图7 导杆3的角加速度曲线 图8 文献[5]中求得的导杆角速度曲线 图9 文献[5]中求得的导杆角加速度曲线