基于模糊最小绝对非线性回归的木材热物性参数预测模型*

曹书博 李嘉豪 周世玉 刘晓平 周玉成

(1.山东建筑大学信息与电气工程学院 济南 250101；2.山东建筑大学热能工程学院 济南 250101)

作为一种生物质材料，木材有针、阔叶材之分，其中针叶材主要由轴向管胞、木射线、木薄壁组织和树脂道组成，阔叶材主要由木纤维、导管分子、木射线和轴向薄壁细胞组成，针、阔叶材的微观结构特征决定了木材的各向异性。木材热扩散系数、体积比热和导热系数是木材材性领域的重要研究内容，其不仅是衡量木材能否适应工作需要的依据，也是对具体应用领域进行基础研究、分析计算和工程设计的关键参数(徐德良，2014)。然而，目前市场上现有木制产品几乎没有提供任何关于木材热物性能的数据，很难根据木材热物性标准在不同类型木材中进行选择(Lagüelaetal.，2015)，木材导热规律研究一直是木材应用领域的经典问题。林铭等(2004)将木材导热与金属导电的宏观规律进行类比，推导出了木材径向热导率数学表达式。Gu等(2005)通过观察木材结构，建立了针叶材弦向和径向导热系数模型。随着人工智能的不断发展，许多研究者将智能算法应用于探索木材导热规律中，并取得了良好效果。杨文斌等(2006)利用BP神经网络对木材径向导热系数进行了建模预测。胡亚才等(2005)提出一个计算横纹导热系数的分形模型和一个预测导热系数的人工神经网络模型，并基于瞬态测量法试验数据对模型进行了验证。徐旭等(2007)提出一个以温度和木材样品孔隙率为输入量、以木材导热系数为输出量的人工神经网络模型，并对木材导热系数进行了非线性拟合。蔡从中等(2009)基于木材在不同影响因素(密度、含水率和比重)下沿横向的导热系数实测数据集，采用粒子群算法寻优的支持向量回归方法建立了木材沿不同方向的导热系数预测模型。由于木材导热系数受其微观结构、密度等多方面因素影响，不同导热模型之间差异巨大(高青等，2008)，迄今为止尚未找到具有足够精确度且适用范围广泛的木材导热系数理论计算方程，通过试验测量木材导热系数几乎成为实际应用过程中确定木材导热系数的唯一有效途径。瞬态平面热源法是测量木材导热系数的常用方法，但该方法计算过程中需要的已知无量纲特征时间函数D(τ)并不能直接计算出来，而是采用迭代法进行估计，这会对测量精度造成影响(丰正功，2017)。

模糊回归分析是评价输出变量与输入变量之间函数关系的一种强有力方法，广泛用于描述、控制和预测输出变量的数值，常用模糊最小二乘法通过使观测值与理论值之间的误差平方和最小来确定模型参数，但由于最小二乘法对异常值敏感，无法得到满意的回归结果(Chukhrovaetal.，2019)。为解决这一问题，引入最小绝对回归方法，即利用观测值与理论值之间的误差绝对值和最小来确定模型参数。Dielman等(1986)验证了当数据中存在异常值时，最小绝对回归方法优于最小二乘法。Chang等(1994)提出了一种基于模糊差值排序的模糊最小绝对回归方法，但是会产生线性规划问题。Torabi等(2007)提出了一种基于“分辨率恒等式”的模糊输入模糊输出线性模型中模糊参数的最小绝对值估计方法。Choi等(2008)采用最小绝对偏差估计量构建模糊回归模型，并使用模糊最小绝对值法估计模糊参数。Kelkinnama等(2012)基于LR模糊数空间的一个新度量介绍了一个新的最小绝对模糊回归模型。Taheri等(2012)通过引入一种新的模糊空间度量方法和最弱三角范数，并用最小绝对偏差方法构建模型。Chachi等(2013)采用广义Hausdorff-metric方法估计模糊参数，建立了一个实数输入模糊输出的最小绝对模糊回归模型。Zeng等(2016)提出一种新的三角模糊数距离测度的前向估计方法，并讨论了不同输入输出数据类型的不同情况以及回归系数。Hesamian等(2017)研究半参数部分线性模型，提出了一种基于曲线拟合法和最小绝对偏差的模糊平滑函数和模糊系数混合估计方法。Hesamian等(2018)将最常用的经典两相法推广到用非参数核函数估计区间值模糊平滑函数，用最小绝对偏差法估计区间值模糊系数，扩展了区间值模糊平滑函数的两阶段估计过程。现有的模糊最小绝对回归方法大多为线性回归方法，即输出变量是输入变量的线性组合，但在对非线性相关的输入输出数据进行建模时会产生较大估计误差。

鉴于此，本研究利用试验测量获得的木材体积比热、径向及弦向导热系数和热扩散系数，建立基于模糊最小绝对非线性回归(fuzzy least absolute nonlinear regression,FLANR)方法的木材体积比热模型和各向异性导热模型，分析木材热物性参数规律，以期为木材导热规律研究、木材热物性评价标准制定提供理论基础和数据支撑。

1 材料与方法

1.1 试验选材

对130种常见木材进行采样，共涉及39个科。试验样品制作过程如图1所示，原木材样品尺寸均为210 mm×100 mm×20 mm，根据试验要求，将每种木材样品加工成2组试验样品，用于测量木材体积比热的试验样品为直径18 mm、厚度2 mm的圆片形样品，用于测量木材导热系数和热扩散系数的试验样品为2块50 mm×50 mm×20 mm的长方体样品。所有试验样品均保存在温度26 ℃、湿度55%的空调室内。每次试验前，将试验样品经烤箱干燥，去除其内部水分，以避免含水率对试验的影响。

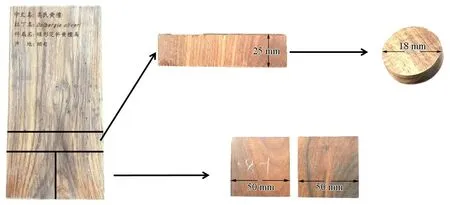
图1 试验样品制作过程示意 Fig.1 The production process of the experimental sample

1.2 试验原理

采用Hot Disk热常数分析仪TPS2200测量130种常见木材样品的体积比热、导热系数和热扩散系数。Hot Disk测量基于瞬态平面热源法，其测量的核心元件为具有连续双螺旋结构的温度依赖探头，外层为双层Kapton保护层。Hot Disk热常数分析仪测量原理如图2所示。

图2 测量探头电路原理Fig.2 The schematic diagram of test probe circuit

根据电桥平衡原理，得到电桥平衡方程如下：

(1)

式中：RS为串联电阻器的电阻值；RL为探头引线的电阻值；R0为探头的初始电阻值；ΔR为电阻随温度变化的增量；R(t)为探头在t时刻的电阻值；ΔU(t)为样品两端检测面电位在t时刻的变化量；I0为瞬态加热初始时通过探头的电流。

求得t时段内样品温度增量：

(2)

式中：α代表探头电阻率的温度系数。

进而由Hot Disk热常数分析仪自带的分析系统得到试验样品的比热、导热系数和热扩散系数。

1.3 试验过程

测量样品各向异性(轴向和径向)导热系数和热扩散系数时需要将样品体积比热作为已知条件。样品体积比热测量使用Hot Disk热常数分析仪的比热模块，将样品置于一个绝热且由高导材料制成的样品支架中，加热空样品支架探头并保存数据到参数文件，每次测量前，将已测取的参数文件导入测量样品试验中，以去除样品支架对测量结果的影响。

样品体积比热测量的具体过程如下：首先将样品置于样品支架中，为其创造一个绝热环境，并将加热时间、加热功率、样品体积、样品质量作为已知条件输入Hot Disk热常数分析仪；然后将同一样品在加热功率100和200 mW时分别进行1次试验，2次试验结果均值作为最终试验结果。为保证试验条件相同，在2次试验之间设置90 min间隔，确保样品散热充分。Hot Disk热常数分析仪每次试验时均会以相同时间间隔均匀采集200个时间点的温升值，用于计算样品体积比热。为保证试验结果准确性，需采集温升变化较为稳定的部分，本研究在计算试验结果时选择第101～200号时间点的温升值参与计算。图3为样品体积比热测量时的瞬态温升图。

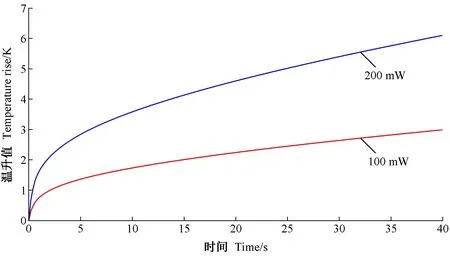
图3 20号比热模块样品瞬态温升图(风车木)Fig.3 The transient temperature rise diagram of No.20 specific heat module sample (Combretum imberbe)

完成样品体积比热测量后，进行样品各向异性(轴向和径向)导热系数和热扩散系数测量。试验使用Hot Disk热常数分析仪的各向异性模块，并将仪器探头更换为双螺旋金属丝覆膜探头。试验时，将金属探头置于已固定的2块长方体木材样本中间，如图4所示。为保证试验结果有效性，体积比热及各向异性(轴向和径向)导热系数和热扩散系数测量使用的试验样本均由同一块木材标本切割得到。同时，为减少外界环境因素对试验结果的影响，每次试验均使用黑色防护罩将试验样本与外界环境隔离。

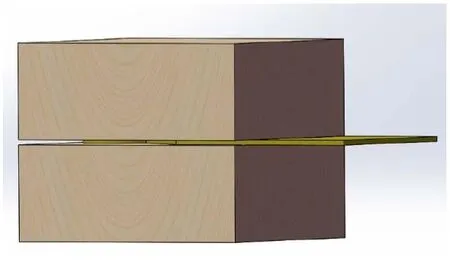
图4 探头测量样品热物性参数示意Fig.4 The schematic diagram of thermophysical parameters of sample measured by probe

样品导热系数和热扩散系数测量的具体过程如下：首先将样品和金属探头固定在样品支架上，并将样品体积比热等参数作为已知条件输入各向异性模块；然后在加热功率50 mW、加热时间80 s的条件下分别进行5次试验，每次试验间隔10 min且试验参数相同；最后对5次测量结果取均值得到样品各向异性(轴向和径向)导热系数和热扩散系数。

需要特别注意的是，木材各向异性导热系数和热扩散系数试验结果中使用的“轴向”和“径向”是以金属探头为参照物，分别与木材样品的径向和弦向相对应，下文涉及所有各向异性试验结果均对应木材样品的径向和弦向。

2 建模与训练

模糊回归分析是一种非常实用的数据分析工具，在许多领域得到广泛应用。模糊最小绝对非线性回归通过引入模糊推理方法，去除现有模糊最小绝对回归的假设，可在输入输出之间非线性数学表达式未知的情况下准确描述数据间的非线性关系。

2.1 模糊最小绝对非线性回归模型构建方法

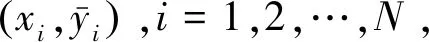
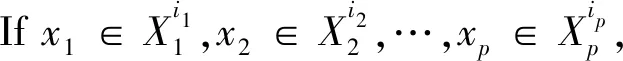
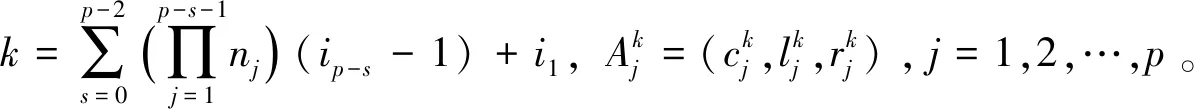
如果一个模糊系统由乘积推理机、单值模糊器以及上述定义的模糊规则库组成，则模糊最小绝对非线性模型可以表示为：

(3)

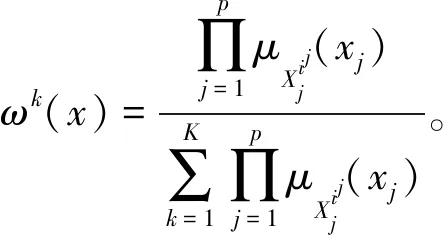
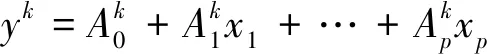
(4)

假设x0=1，由三角模糊数运算(Zengetal.，2017)，模糊最小绝对非线性模型可以改写为：

(5)

根据最小绝对回归准则，即最小化模糊系统输出的估计值与真实值在绝对值距离意义下的误差，定义如下目标函数：

(6)

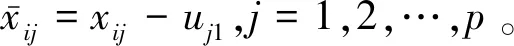
(7)

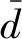
为求解式(7)中的优化问题，定义以下变量：

则在式(7)中，

同理，

进而将式(7)转化为：

(8)

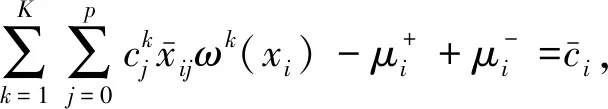
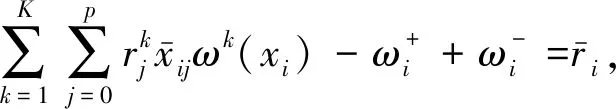
式中：j=1,2,…,p；k=1,2,…,K；i=1,2,…,N。

最后进行坐标反变换，得到模糊最小绝对非线性回归理论模型。

2.2 模糊最小绝对非线性回归模型建模过程

木材体积比热模型输入包括样品质量、样品体积、样品温升参数a、样品温升参数b、加热时间和加热功率，输出为样品体积比热。木材各向异性导热模型输入包括样品厚度、样品轴向深度、样品径向深度、样品质量、探头半径、环境温度、样品温升参数a、样品温升参数b、加热时间和加热功率，输出为样品轴向导热率、轴向热扩散系数、径向导热率和径向热扩散系数。本研究以木材体积比热模型为例介绍模型建立的具体过程。

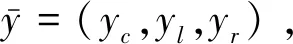
对输入变量的论域进行划分，为每个输入变量分配3个高斯隶属度函数，如图5所示。模糊规则库共由以下729条模糊规则构成：

…

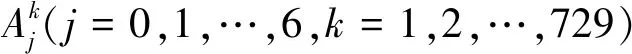
3 结果与分析

3.1 模型评价指标

模型建立后，为定量分析模型计算结果与试验测试结果的拟合程度，使用5种常见评价指标对所建立的木材体积比热模型和各向异性模型进行分析。

木材体积比热模型为多输入单输出模型，使用平均相对误差(mean relative error,MRE)、最大相对误差(maximum relative error,MARE)、均方误差(mean square error,MSE)和拟合度(R2)对模型回归结果进行评价:

(9)

;(10)

(11)

(12)

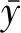
木材各向异性模型为多输入多输出模型，使用拟合优度(goodness of fit,GOF)评价指标进行分析(Wangetal.,2007):

(13)

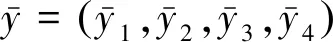
R2理想值为1，MRE、MARE、MSE、GOF理想值为0。

3.2 木材体积比热模型训练与验证结果

本研究使用Hot Disk热常数分析仪测量不同木材体积比热，共产生130组数据。在建模过程中，随机选取其中120组数据作为训练集，剩余10组数据作为验证集。模型的训练与验证结果分别如图6、7所示。建模所用数据集具有一定离散性，很难用数学表达式描述数据间的关系，采用本研究提出的模糊最小绝对非线性回归(FLANR)方法，能够清楚表征在数学表达式未知情况下的非线性关系。

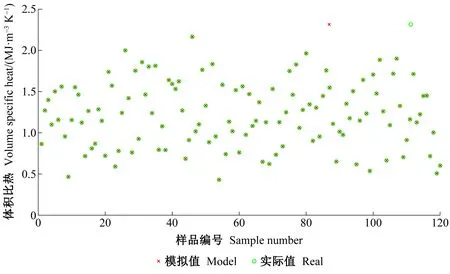
图6 木材体积比热模型训练结果Fig.6 Training results of the wood volume specific heat model

计算模型评价指标可知，模型训练结果的MRE=0.019 3%、MARE=0.041 6%、MSE=0.028 0%、R2=0.999 9，模型验证结果的MRE=0.026 0%、MARE=0.049 1%、MSE=0.035 2%、R2=0.977 6。当建模所用数据集较小时，FLANR仍能得到较好结果。将FLANR建模结果与ANFIS(褚鑫，2020)建模结果进行比较，如表1所示，可以看出，FLANR建立模型与ANFIS建立模型相比，无论是训练还是验证均有更好效果，FLANR建立模型计算时间更短，且具有更强泛化能力。

图7 木材体积比热模型验证结果Fig.7 Validation results of the wood volume specific heat model

表1 FLANR和ANFIS结果比较Tab.1 Comparison of prediction results for FLANR and ANFIS

3.3 木材各向异性导热模型训练与验证结果

与体积比热模型类似，木材各向异性模型同样随机选取120组数据作为训练集，剩余10组数据作为验证集。模型的训练与验证结果分别如图8、9所示。可以看出，采用FLANR方法能够清楚表征多输入多输出模型的非线性关系，所建立木材各向异性导热模型的训练和验证均有较好结果，模型的GOF=5.767 5×10-7。将本研究建立的模型与使用模糊最小二乘法(FLS)建立的模型进行比较，由于建模使用数据集为10输入和4输出，输出变量间具有耦合性，导致 FLS无法准确描述输入输出变量的关系，结果如表2所示。限于文章篇幅，只给出木材轴向导热率的比较结果。

图8 木材各向异性导热模型训练结果Fig.8 Training results of wood anisotropic thermal conductivity model

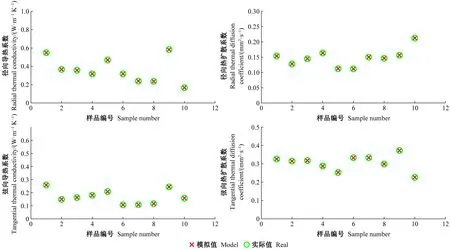
图9 木材各向异性导热模型验证结果Fig.9 Validation results of wood anisotropic thermal conductivity model

由表2可知，使用FLANR建立的模型具有更好的拟合效果和更强的泛化性。与常用模糊最小二乘法相比，模糊最小绝对非线性回归将最小绝对准则与模糊逻辑理论结合，既发挥了模糊信息处理非确定信息的能力，又充分利用了最小绝对准则处理具有一定离散性数据集时表现出快速性和泛化性的优势，同时验证了本研究所构建木材体积比热模型和各向异性导热模型应用于木材热物性参数预测的可行性。

表2 FLANR和FLS结果比较Tab.2 Comparison of prediction results for FLANR and FLS

为验证本研究提出FLANR方法的有效性，将建立的木材各向异性导热模型与蔡从中等(2009)采用支持向量机(SVM)建立的木材径向、弦向导热系数模型进行比较，结果如表3所示。

表3 FLANR和SVM结果比较Tab.3 Comparison of prediction results for FLANR and SVM

由表3可知，FLANR验证结果的MRE、MARE、MSE和R2均优于相应的SVM验证结果。蔡从中等(2009)建立的木材导热系数模型中仅包含28种木材样品，而本研究以130种木材为研究对象；另外，本研究建立木材导热系数模型的输出不仅包括木材径向和弦向导热系数，还包括木材径向和弦向热扩散系数。

4 结论

本研究利用Hot Disk热常数分析仪对130种常见木材进行热物性参数测试，并根据试验结果对木材导热规律进行进一步研究。利用模糊最小绝对非线性回归方法，建立木材体积比热模型和各向异性导热模型，该方法将最小绝对回归方法与模糊逻辑理论相结合，既保持了最小绝对回归准则鲁棒性较强的优点，同时可以在模型数学表达式未知情况下准确描述输入变量与输出变量之间的非线性关系。为验证模糊最小绝对非线性回归方法的有效性，将本研究建立模型与使用ANFIS、FLS和SVM建立模型进行比较，结果表明，本研究方法在用于多输入单输出或多输入多输出模型建立时，预测结果拟合度均能达到0.99以上，平均相对误差、最大相对误差和均方误差的最小值分别为0.19%、0.34%和0.08%，所建立模型具有较好的拟合效果和泛化性。本研究建立的木材体积比热模型和各向异性导热模型为木材热物性评价标准的制定提供了理论基础，同时也为根据木材热物性标准在选择不同类型的木材时提供了依据，对木材产品的标准化和规范化具有重要意义。