基于PCA-SVM的高职院校专业评估体系研究
张延义 赵莹
(滁州职业技术学院 教务处, 安徽 滁州 239000)
高职院校的专业评估,是指在学校管理自我完善的基础之上,依据相关评估标准,针对各专业的教育质量进行评判[1-2]。在实践中,大多是由主管部门领导下(或第三方评估机构)组建的多元化专家组对专业评估指标逐项进行评测、赋分,依据人为设定的指标权重来计算专业评估总分,最后确定专业建设的等级。这种评估流程通常存在以下问题:一是人为设定权重,主观成分大,导致评估结果不合理;二是以总分衡量专业建设的水平,忽视了专业建设的多维度特征,掩盖了某些方面的突出问题;三是组织多元化专家组测评的流程比较复杂,不便于日常管理。为了优化评估工作、提高评估效率,本次研究将依据《国家职业教育改革实施方案》构建高职院校专业评估指标体系[3],利用支持向量机(SVM)在小样本、非线性及高维模式识别问题中的特有优势,以及主成分分析(PCA)中的数据降维技术,针对2所高职院校44个专业的评估指标数据进行专业等级模型训练和专业评估测试。
1 主成分分析和支持向量机理论
1.1 主成分分析(PCA)
主成分分析(principal component analysis,PCA)是最常用的降维方法之一,其思想是通过正交变换法将可能存在相关性的变量转换为一组线性不相关的变量。具体方法是,从原始的空间中按顺序找到一组相互正交的坐标轴,第一个新坐标轴选择原始数据中方差最大的方向,第二个新坐标轴选取与第一个坐标轴正交的平面中使得方差最大的方向,以此类推即得到n个新坐标轴;前面k个新坐标轴中包含了大部分方差,后面的坐标轴可以忽略,以此实现对数据特征的降维处理[4-6]。
将数据集X={x1,x2,x3,…,xn}降到k维,一般过程如下:
(1) 样本矩阵中心化。
(4) 对原始数据进行投影。对特征值从大到小进行排序,并选择其中最大的k个值;然后,将其对应的k个特征向量作为行向量,从而组成特征向量矩阵P[7]。
(5) 获得降维后的新样本数据。将数据转换到k个特征向量构建的新空间Y中,Y=PX。
1.2 支持向量机
支持向量机(support vector machine,SVM)是从线性可分条件下的最优分类面(optimal hyperplane)发展而来,其原理如图1所示。最优分类面,不但能将两类样本点准确无误地分开,而且还能使其分类间隔最大[8]。对于总数为n的线性可分观测样本 (xi,yi),其中xi∈Rn,yi∈{-1,+1},i=1,2,3,…,n,线性判别函数的一般形式为g(x)=wx+b;以H为最优分类线将两类数据分隔开,H1、H2皆为既过距离分类超平面最近的点又平行于分类线的直线,H1、H2之间的距离为分类间隔(m),H1、H2上的训练样本为支持向量[9]。

图1 支持向量机原理示意图
设分类面方程为wx+b=0,其中w是一个垂直于超平面的向量,b为超平面偏置。对判别函数进行归一化处理,使所有样本都能满足|g(x)|≥1,且距离分类面最近的样本|g(x)|=1。若要此分类面对所有样本都能进行正确分类,就必须满足条件:yi(wxi+b)-1≥0,i=1,2,…,n。
对于线性不可分的情况,可以在条件中增加松弛变量ξi和惩罚因子C,将约束条件放宽,从而实现广义的线性分类[9]。对于非线性分类的情况,通过核函数将输入空间映射到高维特征空间,用核函数K(xi,xj)代替最优分类平面中的点积(xi,xj),其优化函数如下:

yi·yj·K(xi,xj)
(1)
相应的判别函数式为:
f(x)=sgn[(w*)T·φ(x)+b*]
(2)
选择不同的核函数就可以构成不同的算法,常用的核函数有:
(1) 多项式核,K(x,xi)=[(x·xi)+1]q。
(3)S形核,K(x,xi)=tanh[v(x·xi)+c]。
采用SVM处理多类别问题:一种方法是通过组合多个二类分类机来实现多类别分类;另一种方法是将两类支持向量机扩展为多类别分类支持向量机。
2 高职院校专业评估指标体系
我国高等职业教育目前已进入高质量发展新阶段。2019年,国务院印发了《国家职业教育改革实施方案》,教育部也启动了“双高”建设行动计划和“现代学徒制”试点工作,为高等职业教育的专业建设赋予了新的内涵。本次研究将在此基础上依据成果导向(OBE)教育理念构建新的高职院校专业评估指标体系,帮助专家组有针对性地评判专业建设的成效。新指标体系中增加了“核心课程满足度、就业满意度、产教融合、校企合作、价值观提升、内部质量保证”等内容,从专业内涵建设和人才培养主动适应市场需求的发展机制等角度构建专业评估指标体系,其中包含9个一级指标和23个二级指标(见表1)。

表1 高职院校专业评估指标体系
3 基于PCA-SVM的专业评估
基于专家组给出的现场专业评估数据与专业等级分类结果,通过数据降维、模型训练与测试实验,将测试结果与专家现场评估的专业等级进行对比,据此判断PCA-SVM专业评估方法的准确率与有效性。
3.1 专业评估数据集
专家组在对两所高职院校的44个专业进行了现场评估,其中部分评估数据如表2所示。
专家组进行现场评估,通常是先成立由学校管理人员、教师、用人单位代表、毕业生等组成的多元化专家组,采用问卷、现场查看测评、学校人才培养状态数据分析、用人单位调查等手段进行评估。针对待评估的专业,分别对照专业评估指标体系中的23个关键评估指标逐项对其进行评测和赋分(满分为10分),然后按照各指标项的权重计算总分,并综合评审数据明确划分出“优秀、良好、一般”等专业分类等级。采用PCA-SVM专业评估方法则无须使用指标项的权重,也不计算总分。

表2 专业评估数据集部分数据
3.2 专业评估数据降维
应用PCA分析实现数据降维。在SAS统计分析系统中新建practice逻辑库,将其导入学校专业评估数据集zypg.sas7bdat,应用princomp函数进行主成分分析。相关语句如下:
proc princomp
data = Practice.zypg
out = Practice.zypg_out
prefix = pc
outstat = Practice.zypg_stat;
var v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 v11 v12 v13 v14 v15 v16 v17 v18 v19 v20 v21 v22 v23;
run
相关系数矩阵的特征值及其累计贡献率如表3所示。其中,特征值越大,则其对应的主成分变量所包含的信息就越多;累计贡献率前4项已达0.940 6,所以选择这4个主成分(即主成分分析产生的新数据集前4项pc1、pc2、pc3、pc4)代替原来专业评估数据中的23项指标,实现数据集降维。降维后的专业评估数据如表4所示。
3.3 专业等级的特征模型训练与测试
应用Libsvm软件进行专业等级特征模型训练与测试。Libsvm软件是台湾大学林智仁等学者开发的SVM模式识别与回归软件包,其特点是对SVM所涉及的参数调节相对较少,默认参数较多[10]。为了保证模型的训练效果,避免各指标项评分值级差过大而导致小特征被大特征所掩盖的情况,在开始特征模型训练前对专业测评数据在[0,1] 区间进行归一化处理。
(1) Libsvm软件中的核函数选择。专业评估是对专业建设质量的综合判断,专业评估指标体系又是一个多维、非线性的模型,所以选择了分类(C-SVC)模型、径向基形式(RBF)核函数,最终生成式(3)所示决策函数:

(3)
式中:xi为支持向量;x为待预测标签的样本;‖xi-x‖为二范数距离;b为一个标量数值;wi为支持向量的系数。
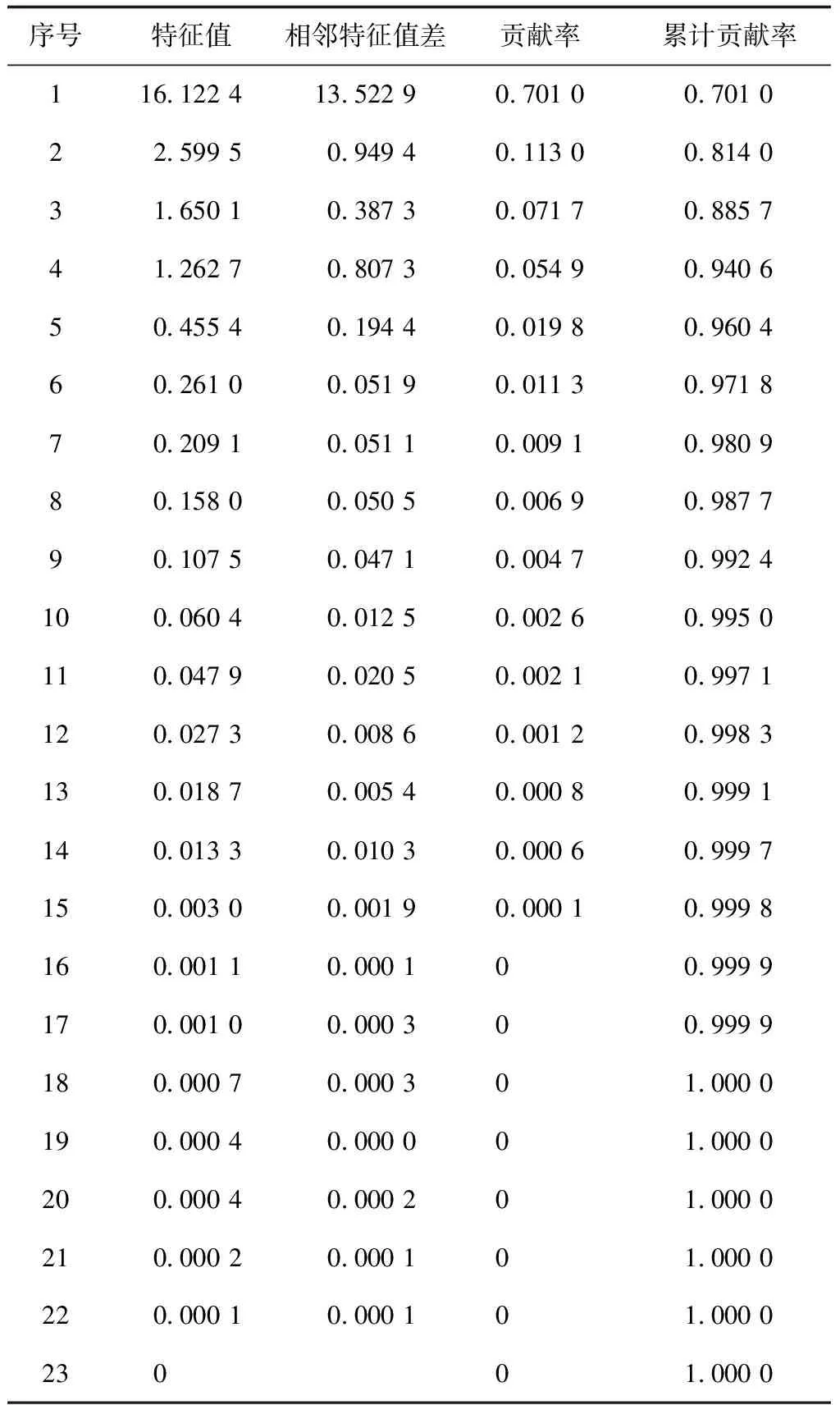
表3 相关系数矩阵的特征值及其累计贡献率

表4 降维后的4个主成分数据
(2) Libsvm软件中的参数选择。调用网格参数寻优函数SVMcgForClass实现c、g参数寻优,本例寻优结果如图2、图3所示。其中,降维前的专业评估数据集最佳参数为c=4,g=0.015 6;降维后对应的专业评估数据集最佳参数为c=4,g=1。

图2 降维前的专业评估参数c、g寻优结果

图3 降维后的专业评估参数c、g寻优结果
接下来进行模型训练与测试:
(1) 对降维前的数据进行模型训练与测试。从以上数据集中,随机选择21项专业评估数据作为专业训练样本集,其余23项专业评估数据作为专业测试样本集;然后,分别调用Svmstrain模型训练函数、Svmpredict测试函数,获得的分类准确率为91.304 3%。结果表明,应用Libsvm 软件得到的专业分类结果与专家组评估得出的专业建设结果吻合率为91.304 3%。
(2) 对降维后的数据进行模型训练与测试。选择专业评估数据中降维后对应的主成分数据,再分别调用Svmstrain模型训练函数与Svmpredict测试函数,获得的分类准确率为95.652 2%。此次准确率比降维前提高了4.347 9%(见表5)。
通过数据降维,去除了样本中信息的重叠部分,提高了分类精度。PCA-SVM评估方法与专家组现场评估结果的吻合率高达95.652 2%,即在23个测试专业中仅有1个专业分类相异。这一个相异分类的原因是,专家组对该专业的评估指标赋分或综合评审的尺度不一。其余22个专业分类均相符,这表明PCA-SVM评估方法的可靠性,可代替专家组的现场评估工作。

表5 降维前后专业评估最佳参数及分类准确率
4 结 语
在本次研究中,构建了高职院校专业评估体系,引入主成分分析(PCA)和支持向量机(SVM)技术进行分析。该体系有利于专业建设成效分析与质量评价,其中包括9个一级指标和23个二级指标。应用Libsvm软件进行专业等级特征模型训练与测试实验,验证了该体系的合理性。采用PCA-SVM专业评估方法,可以充分发挥SVM在小样本、非线性及高维模式识别以及主成分分析数据降维方面的优势,训练专业等级特征模型,以取代专业组现场评估。该评估方法可避免人为设定权重所导致的主观性偏差,能够体现专业建设的多维特征,提高专业评估的工作效率。

