国产化水下油气生产系统可靠性分配研究*

刘 超 胡忠前 刘 健 柳梦雪 肖文生

(1.中国石油大学(华东)机电工程学院 2.海洋物探及勘探设备国家工程实验室 3.中海油研究总院有限责任公司)

0 引 言

近年来，随着陆上石油资源逐渐枯竭，世界各国越来越重视海上油气田的勘探和开发[1]。水下油气生产系统作为海洋油气的主流开发模式[2]，具有节省开采费用、油气输送量大、油气输送连续快捷及油气开采效率高等诸多优点，备受国内外石油公司关注并不断发展。国内水下油气生产系统研究较晚，技术水平还处于初步发展阶段，还未成功投产一套完整的国产化水下油气生产系统[3]。因此，开展水下油气生产系统可靠性相关研究，为保障国产化水下油气生产系统的成功实施，提高我国海洋油气开发竞技水平具有重要意义。

可靠性分配作为系统可靠性设计的主要环节，目的是将系统规定的可靠度指标按照一定的准则分配到各子单元，得到更加合理的系统产品设计参数[4]。早期的可靠性分配法一般是对简单系统进行研究，主要包括比例分配法[5]、等分配法[6]、加权分配法[7]、评分分配法[8]及重要度分配法[9]等，这些方法考虑因素单一，不适用于受多因素耦合影响的复杂系统。目前，可靠性分配研究朝着考虑多因素耦合影响的方向发展，层次分析法(AHP)是一种可以综合考虑系统多种评价因素的数学方法[10-11]，该方法的提出为可靠性分配提供了一种新的思路，并在复杂系统可靠性分析中得到广泛应用。彭宝华等[12]针对复杂系统可靠性分配，提出了层次分配法；谢红军等[13]以某型控制系统作为研究对象，将层次分析法应用到系统可靠性分配实际中；SUN Q.等[14]在传统层次分配法的基础上引进修正区间进行定量分析，并将其应用到电液压系统中；邵延峰等[15]对复杂串、并联系统的可靠性分配法进行介绍和对比，发现利用层次分配法能够综合考虑多因素且更客观、更系统地进行可靠性分配。

本文将层次分配法运用到水下油气生产系统可靠性分配研究中。考虑到系统处于产品设计初期阶段，无法获取可靠性相关数据，通过引入相似产品分配法，并参考国内外已成功实施生产的系统失效数据库，来综合分析国产化系统各单元可靠性分配权重系数，进而弥补层次分配法带来的主观误差。基于此，提出一种相似产品分配法和层次分析法结合的复合分配法，并将该方法应用到典型国产化水下油气生产系统可靠性分配实例中，分析结果表明，所提方法可在很大程度上优化系统可靠性分配，进而更加合理化地指导系统可靠性设计。

1 可靠性分配法

系统可靠性分配的实质是系统可靠性最优化问题，基本思想是根据规定指标、预测数据和生产工作条件等，将可靠性指标合理地分配给各单元，实际上是求解下列不等式：

(1)

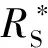
在系统可靠性分配方法中，等分配法存在与实际情况分配不合理的缺点，评分分配法主观性比较强[8]。相似产品分配法是在两个分析系统类型及结构等相似条件下提出来的，按照比例分配到新系统中。在复杂系统可靠性分配时，需要综合考虑多种因素影响，采用单一的可靠性分配法不能满足要求。复合分配法可以综合多种分配法的优点，通过考虑各种分配方法相对系统分配的重要程度，来对各分配法赋予不同的权重系数。

2 复合可靠性分配法基本流程

本文在传统可靠性分配方法中提出两个创新点，通过建立专家评分系统来构造判断矩阵，运用复合分配法进行系统可靠性分配，具体流程如图1所示。

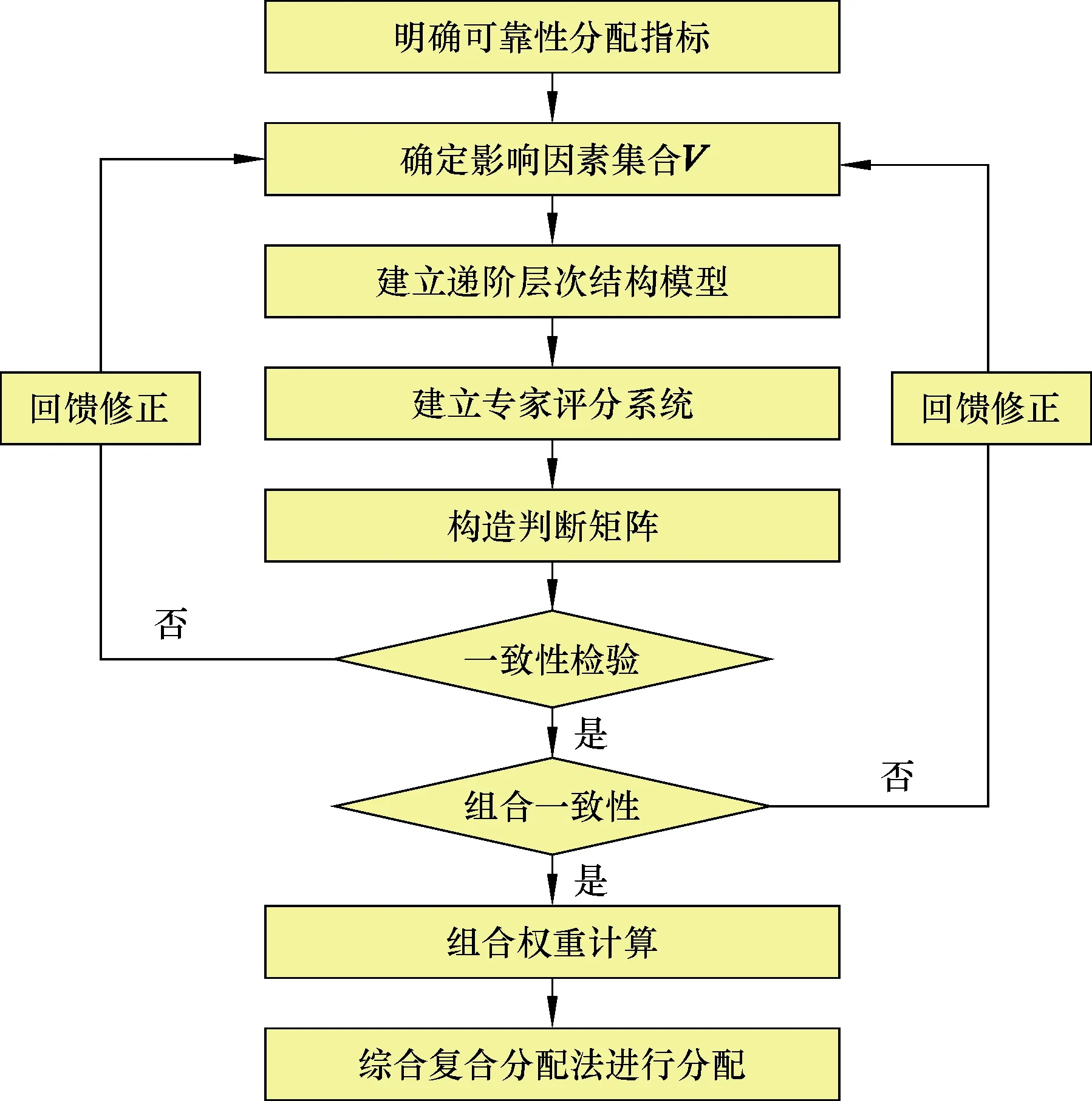
图1 可靠性分配流程图

2.1 明确可靠性分配指标

分析研究对象，选取合理的可靠性分配指标。系统目标量化可以通过选用失效率等可靠性指标来体现，将系统可靠性指标按照分配权重系数合理地分配给各个子单元。

2.2 确定评价影响因素集合V

评价因素的选取非常重要，直接决定了系统分配结果是否可以指导产品设计，所以要综合考虑系统所处环境和故障机制，选取能反映系统实际工作情况的影响因素集合V={v1,v2,……,vn}。

2.3 建立系统递阶层次模型

根据系统、评价因素和设备之间的关系进行层次划分，构建系统递阶层次模型，如图2所示。

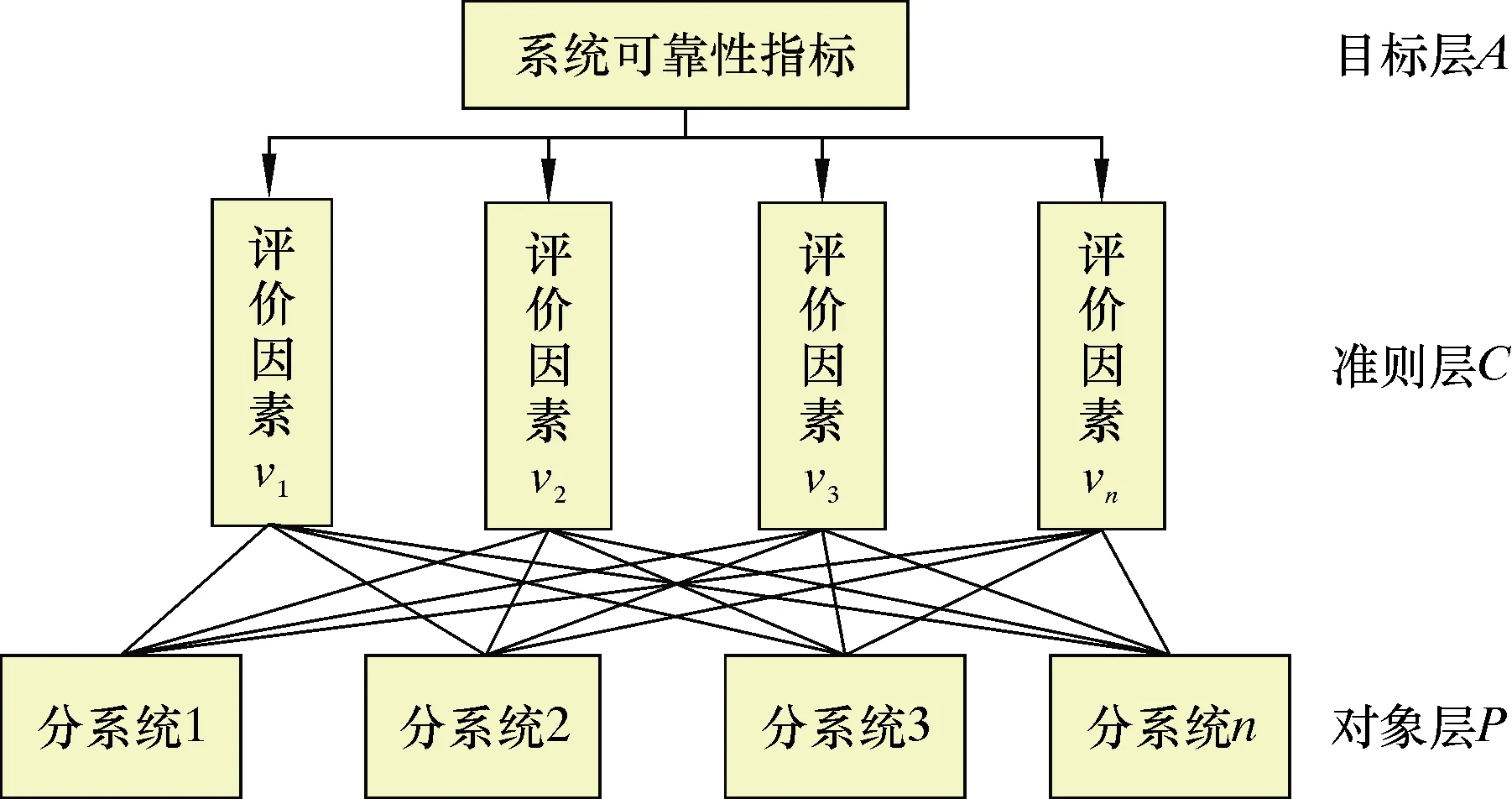
图2 系统递阶层次模型

图2中目标层A表示系统可靠性指标，中间层准则层C表示评价影响因素V，对象层P表示各个分系统。上层因素可以支配下层因素，模型层次数和系统影响因素的复杂程度及数量有关。

2.4 建立专家评分系统

β=(β1，β2，β3，……，βk)

(2)

2.5 构造判断矩阵

计算评价因素和评价对象的相对权重比，即构造各层次之间的判断矩阵M，通过客观判断来反映专家的决策意愿。其中，标度是将专家的定性决策转化为定量分析的评价尺度，反映出各层因素之间的重要关联度，选择合适的标度十分重要。表1列出了4种常用的标度[16]，并绘制了相应的曲线对比图，如图3所示。

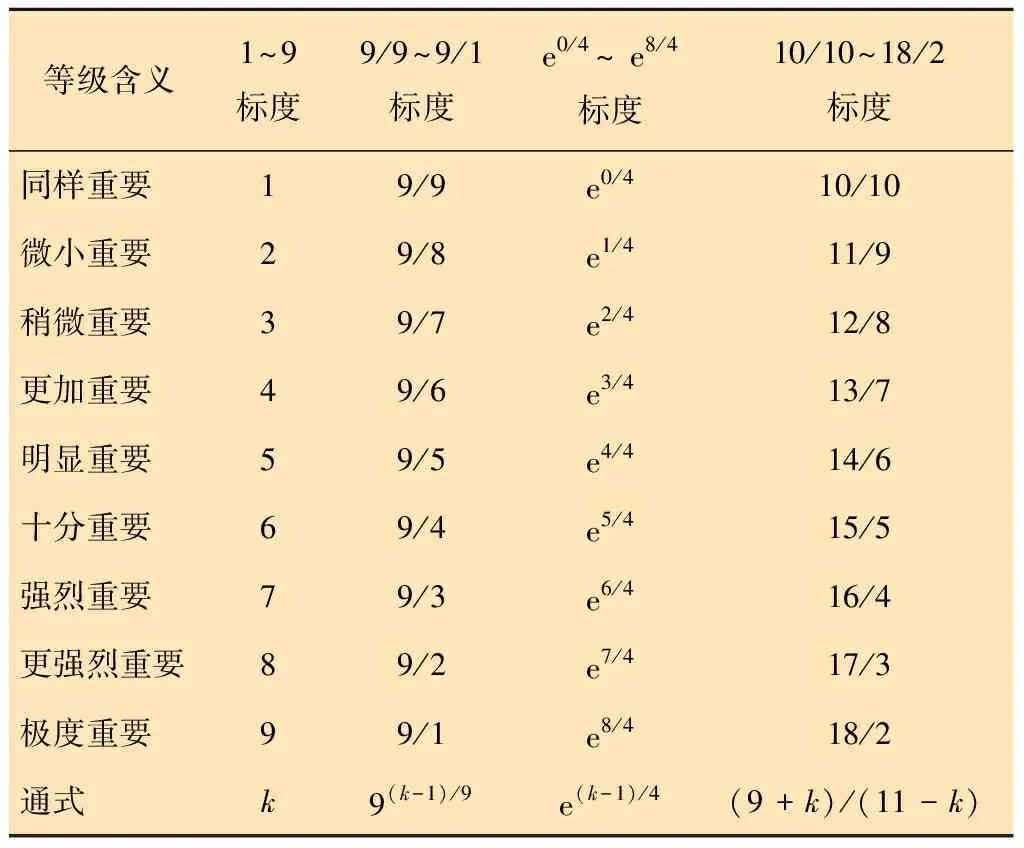
表1 4种常用标度的比较

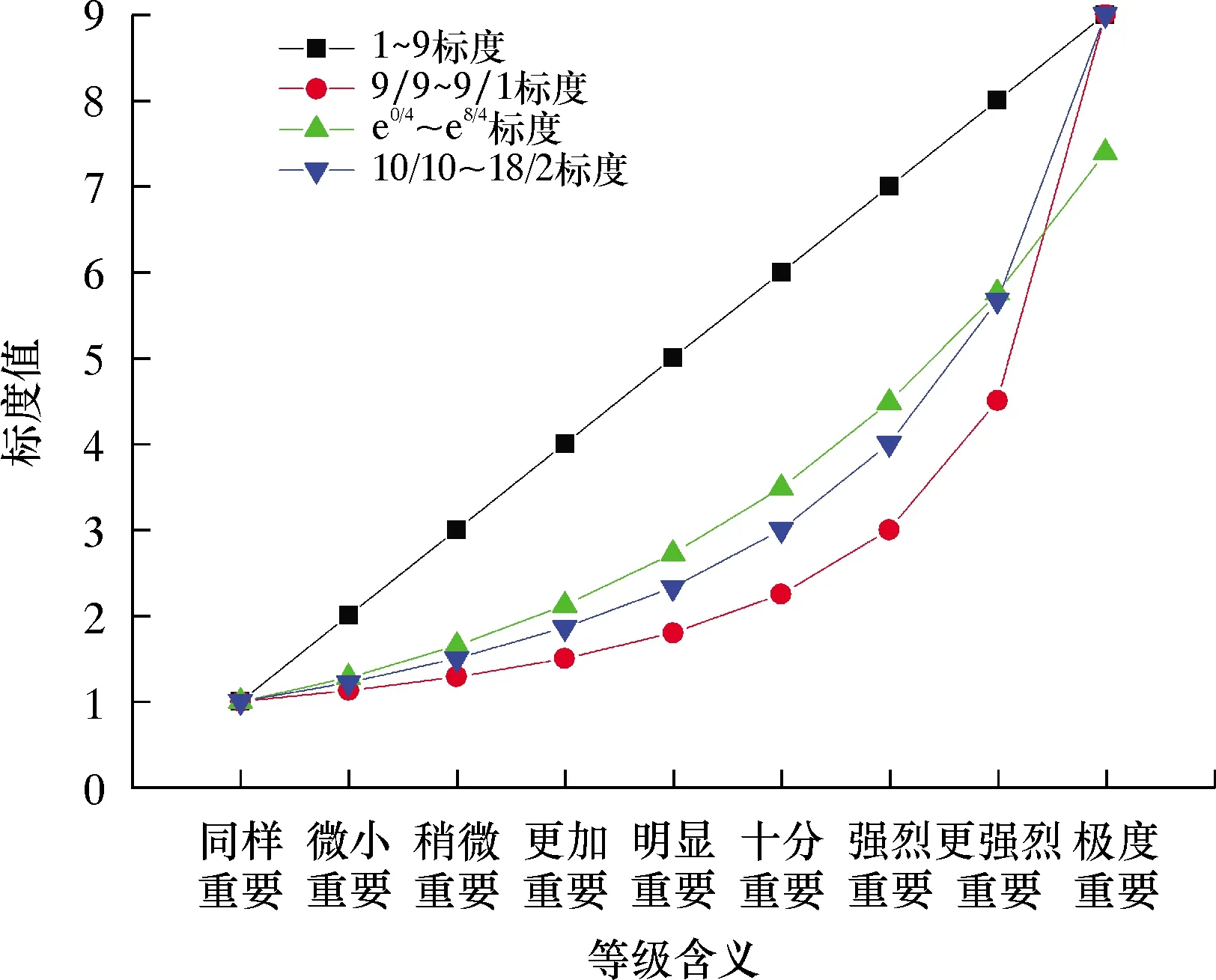
图3 4种常用标度的曲线对比

从图3可以看出，4种标度的曲线走势基本相同，很难判断出哪种标度更加符合评价标准，因此，需要将4种标度各自9个等级进一步进行一致性CI检验和最大偏差S计算，如表2所示。

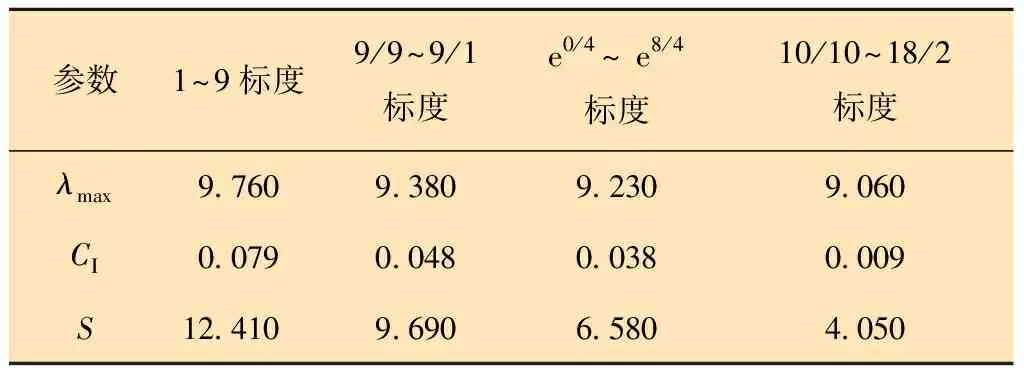
表2 4种标度相应的CI和S

由表2可以看出，10/10～18/2标度的CI和S值相比其他标度数值要小得多，更加准确反映出各层因素间的关联度，因此本文选取10/10～18/2标度来进行定量评价。各个标度含义如表3所示。

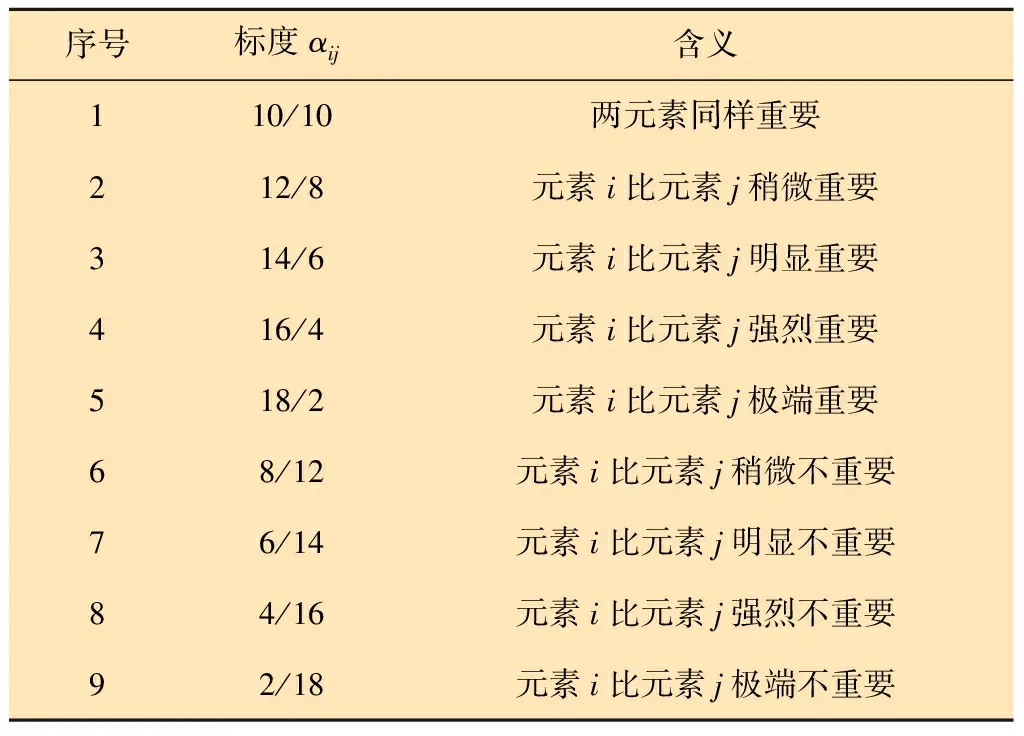
表3 判断矩阵标度含义

构建判断矩阵的具体方法：假设构建准则层C上各因素相对于目标层A的判断矩阵，选取k个相关领域专家，依次对比准则层C上评价因素vi和vj的影响大小，设第p(1≤p≤k)名专家对准则层C的判断矩阵为Mcp, 矩阵任意元素用aijp来表示，即：

(3)

(4)

2.6 计算权重向量并做一致性检验

对于判断矩阵Mc，求出最大特征根λmax及特征向量ω=(ω1，ω2，ω3，……，ωn)，特征向量一般采用和法进行计算。对判断矩阵每行元素进行求和，再进行规范化，得权重向量：

(5)

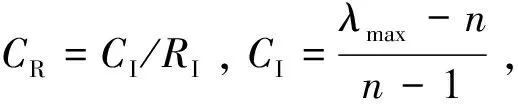
表4 随机一致性指标RI

当CR<0.1时，判断矩阵符合一致性检验要求，特征向量ω=(ω1，ω2，……，ωn)即为权向量。如若不满足，需要继续进行判断矩阵修正，直到满足要求为止。

2.7 组合权向量计算

组合权向量的计算实际是求解对象层P相对于目标层A的权重系数，设准则层C相对于目标层A的相对权重为：

(6)

对象层P相对于准则层C上的相对权重为：

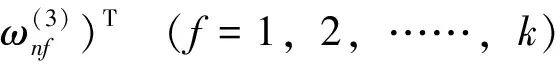
(7)

进而，得出对象层P相对于目标层A的组合权向量：

(8)

通过和法归一化处理，得到组合权向量ki，表示对象层P上各单元对系统的重要程度：

(9)

2.8 可靠性指标分配

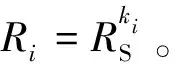
选定AHP法和相似产品分配法并引入分配系数θ1、θ2，且满足θ1+θ2=1，同时有：

(10)

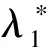
对集合θ=(θ1,θ2)，依据对目标影响的程度进行对比，构造出判别矩阵A=(ψij)2×2，矩阵中任一元素ψij表示θi比θj的相对重要程度。

通过和法进行归一化处理，求得最终权向量：

(11)

3 水下油气生产系统可靠性分配

水下油气生产系统是指一系列安装在海底并进行采油作业的设备总集，参考《水下生产系统手册》[17]和《API IP 17A》[18]对系统进行层次界定和划分：主要由水下控制子系统、立管子系统、海底管线子系统、水下管汇子系统、水下井口装置及采油树子系统组成，根据子系统之间的功能关系建立水下油气生产系统模型，如图4所示。图4中，红色线段代表水下控制系统的线路网以及化学试剂注入管线等，黑色线代表油气水的运输管线及注水管线，子系统之间通过终端接口进行相互作用，将采出的油气水多相流体从海底输送到海上浮式油船进行处理。

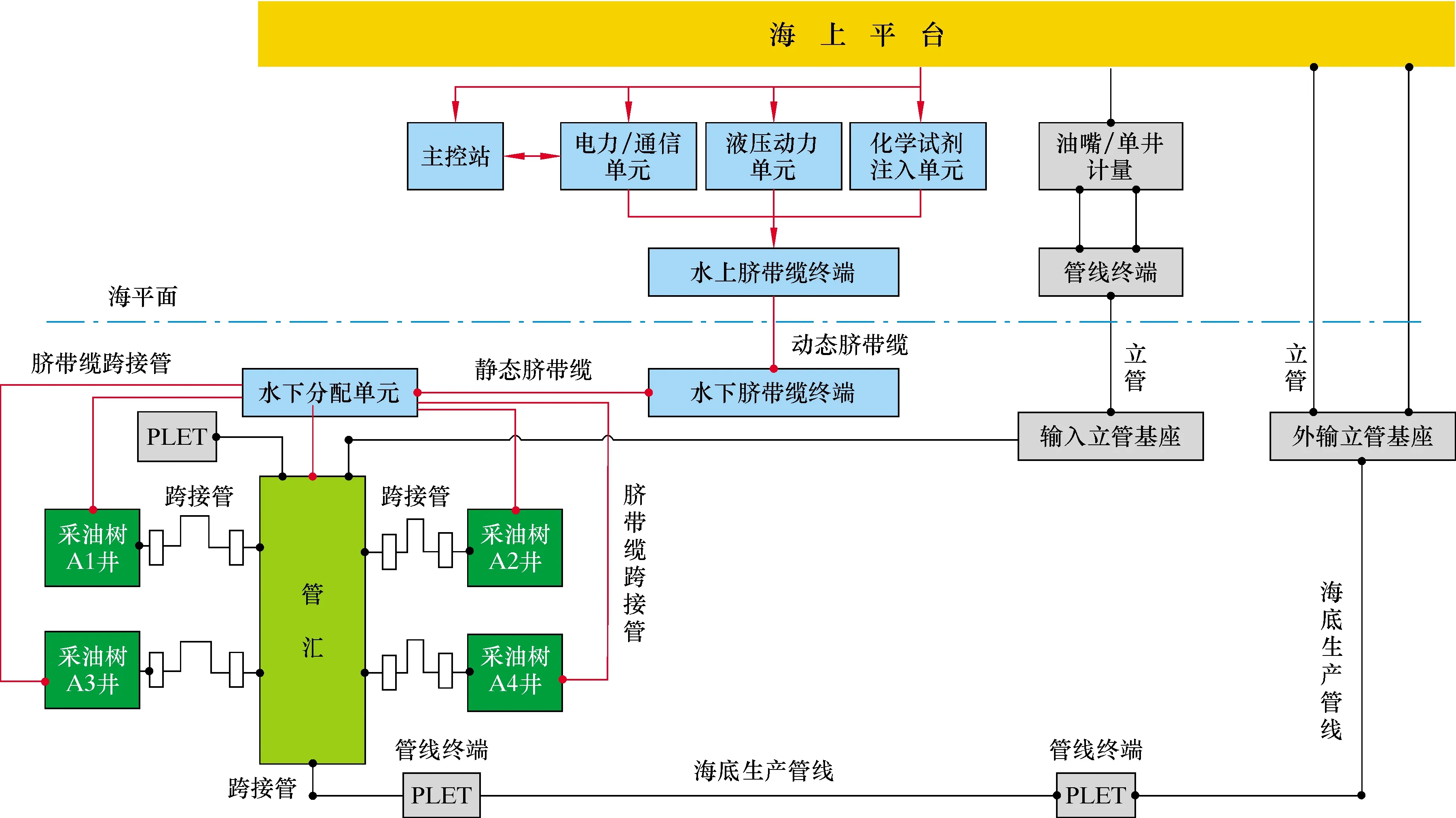
图4 水下油气生产系统模型

3.1 建立系统可靠性框图

可靠性框图(RBD)根据系统组成单元之间的功能相关性以及逻辑性构建[19]，由表示系统单元的方框、逻辑关系、有向线段和各节点组成。本文将水下油气生产系统按照系统级、子系统级以及设备级逐级展开，建立水下油气生产系统各设备之间以串联的形式组合而成的可靠性框图，如图5所示。

图5 水下油气生产系统的可靠性框图

由于系统结构复杂，各子系统之间的可靠性要求也不尽相同，所以本文采取一次分配和再分配的方法，先经一次分配到子系统，然后再分配到设备级。简化后的系统可靠性框图如图6所示。

图6 系统可靠性简化框图

根据图6，可得出系统可靠性的表达式：

(12)

3.2 系统可靠性分配分析

3.2.1 可靠性指标选择

在工程实际中，通常根据不同类型的产品复杂程度、不同的故障特点等进行可靠性指标的选取。对于复杂系统而言，失效率是最直接的评价指标，选择失效率作为分配指标可以使设计人员得到直观明确的分配结果。国产化水下油气生产系统要求可靠度不低于99%，考虑到可靠性分配中会出现评价因素分析不周全等情况，往往需要预留5%～10%的可靠性分配余量，本文初步设计系统可靠度RS=0.995, 则失效率λS=0.005 012，系统中各设备的寿命服从指数分布。

3.2.2 确定评价对象的影响因素集合V

结合我国海域实际情况，综合考虑系统的复杂程度、技术工艺水平、工作环境、故障发生频率、故障后果严重程度及维修影响因素，确定评价对象的影响因素集合：V={v1,v2,v3,v4,v5,v6}。

3.2.3 建立系统层次结构模型

定义水下油气生产系统分配目标层、准则层和对象层，构建系统递阶层次模型，如图7所示。

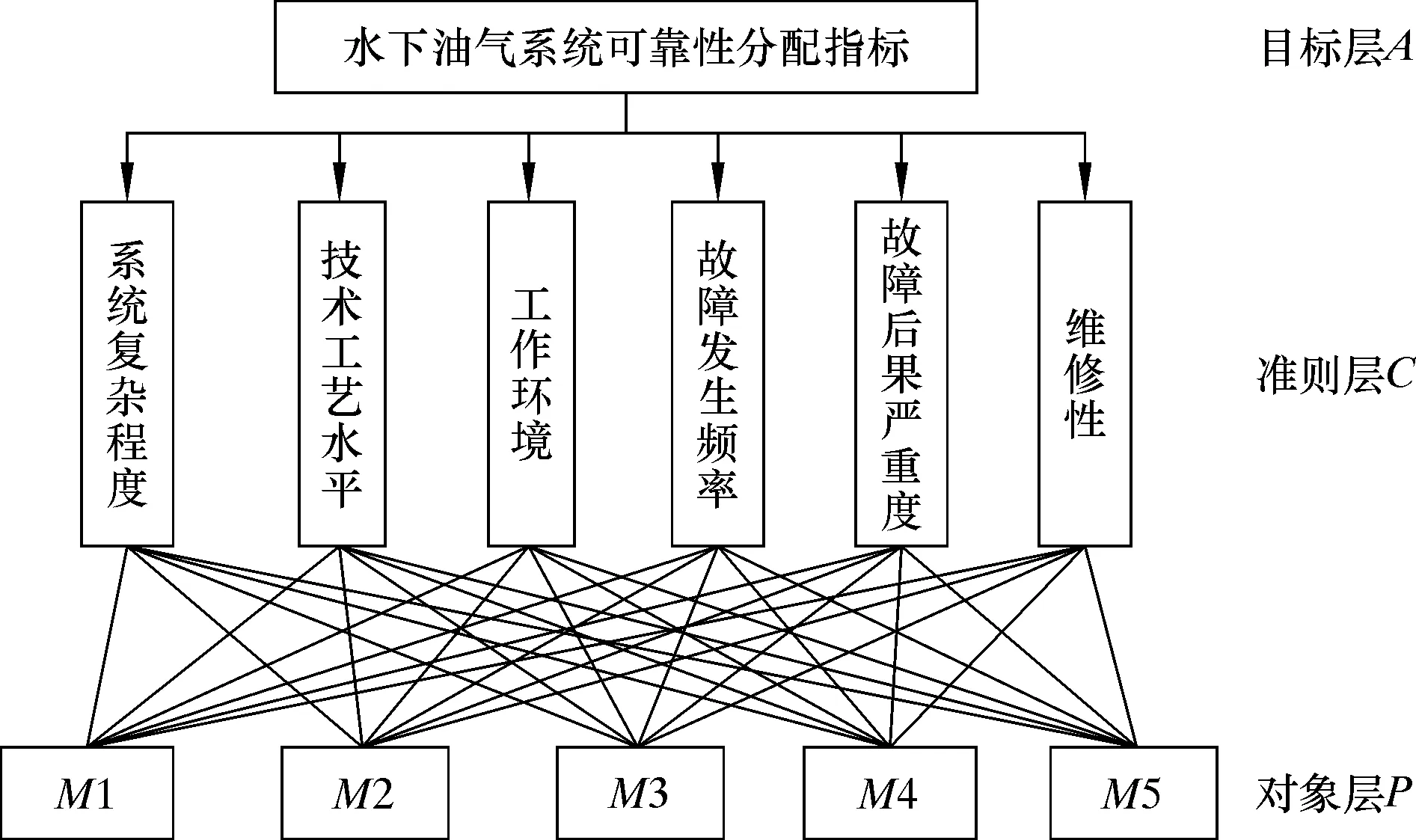
图7 系统递阶层次模型

第一层为目标层A，表示系统的总故障率；第二层为准则层C，表示相对于目标层而选择的评价因素集合：v1系统复杂程度、v2技术工艺水平、v3工作环境、v4故障发生频率、v5故障后果严重程度、v6维修性；第三层为对象层P：M1～M5对应各子系统。

3.2.4 建立专家评分系统

选取6名海洋与石油装备领域的专家进行水下油气生产系统可靠性影响因素评价，并搭建系统评价体系，通过MATLAB计算及归一化处理得到各专家权重比，即有：

β=(β1，β2，β3，β4，β5，β6)=

(0.219 6，0.186 9，0.168 2，0.154 2，

0.144 9，0.126 2)

(13)

3.2.5 构造判断矩阵

6名专家分别针对准则层C相对于目标层A的重要程度进行评比，记录专家给出“同样重要、稍微重要、明显重要”等语言，并将语言表达通过标度量化成各个判断矩阵Mcp(1≤p≤6)。

(14)

(15)

(16)

(17)

(18)

(19)

计算得出矩阵Mc1～Mc6的最大特征根λmax=(6.031 8,6.028 6,6.071 2,6.003 8,6.024 4)，且每个矩阵均满足CR<0.1，符合一致性检验要求。再根据专家权重系数集β=(β1，β2，β3，β4，β5，β6)，计算出准则层C上评价因素相对于目标层A的最终权重比：

ω(1)=(0.138 1，0.107 9，0.096 3，

0.281 6，0.233 6，0.142 4)T

(20)

同理可得对象层P各单元相对于准则层C上各元素的最终判断矩阵MP1～MP5(由于文章篇幅问题，不一一列出)，准则层的准则Cf对于对象层P上的n个单元相对权重分别为：

(21)

(22)

(23)

(24)

(25)

(26)

则目标层A对于对象层P的组合权向量为：

(27)

通过MATLAB计算并进行归一化处理,最终得到组合权向量：

k=(k1,k2,k3,k4,k5)=

(0.337 6,0.091 4,0.143 3,0.164 2,0.263 5)

(28)

3.2.6 复合分配法计算

本文将选用AHP和相似产品分配法结合的复合分配法进行水下油气生产系统可靠性分配研究。

(2)参考水下油气生产系统失效数据库OREDA，根据相似产品分配法，将系统可靠性指标按照一定比例要求分配到国产化水下油气生产系统的各子系统为λ2i。

3.2.7 二次可靠性分配

将分配到各子系统的可靠性指标进行二次可靠性分配，分配到下属的设备级别，由于各子系统所处的条件差异较大，需重新构建各子系统的递阶层次模型。通过专家系统来构造各子系统的判断矩阵，经复合分配法求解各设备级别的权重系数，得到各设备单元失效率，分配过程同一次分配，本文直接给出最终的可靠性分配结果(见表5和表6)。

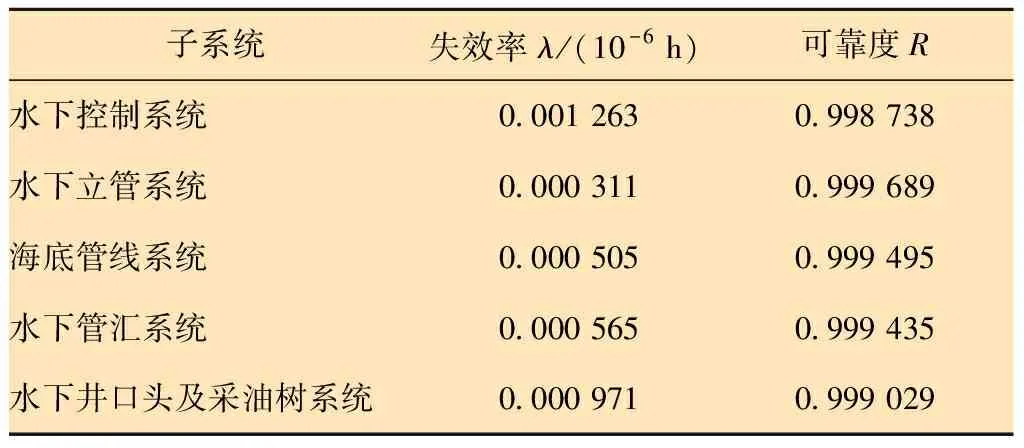
表5 水下油气生产系统子系统级的可靠性分配结果

表6 水下油气生产系统设备级的可靠性分配结果

3.2.8 可靠性分配方法对比

以典型国产化水下油气生产系统为案例，进行可靠性分配方法研究，将相似产品分配法、AHP以及本文提出的复合分配法3种方法进行分析对比，结果如图8所示。从图8可以看出，AHP分配法求解出的系统分配系数相对较大，这对系统产品设计要求特别高，从而增加产品设计和生产成本。相似产品分配法求解出的系统分配系数相对较低，产品设计可能不满足整体系统的可靠性要求，导致系统使用寿命缩短。复合分配法综合考虑这两种分配法的优缺点，优化系统可靠性分配系数，使系统可靠性设计更加合理，分析结果更加贴近实际需求。

图8 系统可靠性分配方法对比

4 结 论

(1)在传统层次分配法的基础上，提出一种基于相似产品分配法和AHP结合的复合可靠性分配法，该方法综合考虑多种因素影响，有效弥补了AHP分析的主观性误差，能够更为客观且准确地进行可靠性分配。

(2)层次分配法的关键环节是构建判断矩阵，本文通过搭建专家评分系统来建立判断矩阵，针对经验能力不同的专家利用AHP来赋予不同的权重值，科学合理地综合多位决策者的意见，尽可能消除主观差异，从而大幅度提高系统可靠性分配的准确性。

(3)以典型国产化水下油气生产系统作为研究对象，建立系统模型及其可靠性框图，并详细阐述了复合可靠性分配法的具体应用实例。实例分析表明，本文所提出的复合可靠性分配法能够优化复杂系统可靠性分配系数，可对国产化水下油气生产系统自主设计阶段工作提供一定的指导，分析过程可推广到类似水下油气生产系统，具有一定的工程实际参考价值。