基于耦合H型谐振腔的双重Fano共振研究

尤鑫晨，关建飞

(南京邮电大学 电子与光学工程学院、微电子学院，南京 210023)

0 引 言

Fano共振能够产生典型非对称响应谱线形状，显著增大透射谱线的波谱分辨率。在相干量子系统[1]、等离激元纳米颗粒[2-3]及电磁超构材料[4-5]等纳米技术领域吸引了广泛的关注。表面等离子激元(Surface Plasmon Polaritons, SPPs) 由于能够突破衍射极限[6]，并具有很强的局域场增强特点[7]，可以实现纳米尺度的光信息传输与处理，逐渐成为Fano谐振效应的重要研究场景[8-9]。基于离散态和连续态之间的干涉效应产生Fano共振的基本原理，可人工构造的异质结低聚物超构材料[4]以及双金属棒与金属圆盘为基本单元的超构材料[5]中都可实现双重Fano共振效应，并产生具有陡峭边沿的非对称透射谱线，可以为实现高分辨率传感提供设计思路。

近年来，金属-电介质-金属(Metal-Dielectric-Metal，MDM)型波导凭借其有效的模场束缚及较低的传输损耗而成为SPPs较为理想的传输线路。在MDM波导实现Fano共振，可以为微纳结构的折射率传感提供一种有效的选择方案[10]。例如，安厚霖等[11]提出的含T型空腔的单挡板MDM波导结构，得到了灵敏度为1 620 nm/RIU的 Fano透射峰;韩帅涛等[12]提出了单挡板MDM波导耦合圆盘腔的波导结构，产生了典型的双Fano共振;石悦[13]等人提出了由开口方环共振空腔耦合MDM波导结构,实现了灵敏度可达1 600 nm/RIU的Fano透射峰;陈颖等[14]提出含金属挡板MDM波导耦合横置T型腔结构，实现了多重独立可调谐Fano共振。上述研究表明，MDM波导中嵌入金属挡板可以实现低透射率以及宽光谱的连续态，这为激发Fano共振提供了有利条件。但在同一谐振腔内实现透射率较高且间距可调的双重Fano共振透射峰却具有一定难度。Fu H X等[15]提出了水平对称失谐的正交双支节腔耦合MDM波导结构，实现了双重Fano共振效应，并分析了水平失谐量对双Fano峰的影响，在400 nm×500 nm的尺度下得到了灵敏度分别为1 040 和980 nm/RIU的双重Fano共振透射峰。

本文提出了一种含单金属挡板的MDM波导耦合H型谐振腔的波导结构。仿真结果表明，H型谐振腔内可以产生沿水平横向及竖直纵向的两类一阶谐振模式，且两类一阶谐振模都能与金属挡板产生的反射膜耦合产生Fano共振进而形成两个边沿陡峭的反对称透射峰。文中采用有限元分析法分析了H腔结构参数对耦合波导透射谱线的影响，并计算出了双重Fano共振产生的透射双峰的灵敏度分别达到了750 和1 360 nm/RIU，该结构为片上集成的纳米光学折射率传感器设计提供了理论参考。

1 理论模型及响应分析

图1所示为含金属挡板的MDM波导耦合H型谐振腔结构的二维平面示意图。金属挡板的厚度为s=20 nm，g为H型谐振腔与波导的耦合距离，初始设置为10 nm；L1为H型谐振腔中横向矩形腔的长度；L2为H型谐振腔中两边竖直方向对称矩形腔的长度，初始设置为L1=100 nm及L2=300 nm；横腔与竖腔的宽度t均设定为100 nm；h为H型谐振腔中横向矩形腔相对于竖腔最底端的高度；w为入射及出射波导的宽度。

图1 含金属挡板MDM波导耦合H型谐振腔结构

图1中，白色区域为空气介质填充区域，空气的相对介电常数εd=1；绿色区域为金属银，其相对介电常数εm(ω)由德鲁德模型[16]表示如下：

式中：ε∞=3.7为无穷大频率对应的介电常数；ωp=1.38×1016rad/s为等离子振荡频率；i为虚数单位；γ=2.73×1013rad/s为电子碰撞频率；ω为入射光的角频率。为进一步分析模型的光频响应特性，本文采用有限元软件Comsol Multiphysics建立了二维平面模型，采用频域分析模块对波导结构的透射谱及模场分布进行数值计算。

为保证MDM波导中只有传输距离较长的反对称耦合模[17]能够传播，波导宽度w固定为50 nm[18]。当入射光波从模型左侧端口边界入射时，在MDM波导中间层产生亚波长尺度的SPPs导波模式。由于金属挡板的引入，在挡板左侧边界上发生的界面反射将导致一部分SPPs能量返回入射端口；同时有较少的一部分SPPs能量基于隧穿效应透过金属挡板向右侧的透射波导传输，并最终从右侧端口出射。不同波长的透射率计算公式为T=Pout/Pin[19]，Pin为入射光功率，Pout为出射光功率。当入射波长λ满足谐振条件[20-23]：

式中：neff为MDM波导中导模SPPs的模式有效折射率，计算公式为neff=β/k0，β为SPPs模式传播常数，k0=2π/λ0为入射光的自由空间波矢,λ0为入射光波的波长；Leff为有效腔长；正整数m为谐振阶数；φ为SPPs在电介质-金属交界面发生反射所引起的相移变化。入射波导中的SPPs能量通过近场耦合进入H型谐振腔中，并在腔内形成稳定的驻波场进而有效提升腔内的能量。当H型腔中的谐振能量耦合进入出射波导并向右传输到出射端口时，可以显著增加透射率从而形成尖锐的透射峰。

图2所示为3种波导结构的透射谱线。仿真结果表明，当波导系统中只含有金属挡板未引入谐振腔时，输出端口会产生透射率很低的连续透射谱，如图2中黑色曲线所示。而当无金属挡板MDM直波导与H型腔耦合时将产生中心波长分别位于830 和1 390 nm的两个透射极小值，分别对应H型腔中的两个离散态谐振模式，如图2中红色曲线所示。当含有金属挡板的波导与H型谐振腔侧向耦合时，挡板产生的连续态反射传输模将与H型腔中的两个离散态谐振模相互耦合形成两个非对称的Fano共振透射峰，如图2中蓝色曲线所示。图2中波长位于810 和1 355 nm的两个透射峰分别记为FR2与FR1。

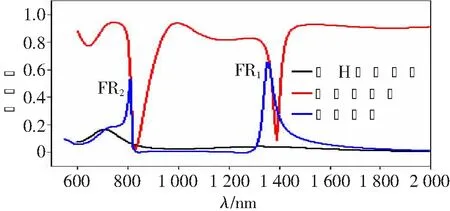
图2 3种波导结构的透射谱线

为了更加直观地解释Fano共振透射峰的形成机理，图2所示蓝色曲线中透射极大值与极小值对应的磁场分量Hz的模式分布如图3所示。图3(a)所示为透射峰FR2对应的模场分布，当λ=810 nm时，H型腔右侧的竖腔中磁场强度得到显著增强。这一趋势表明由入射波导耦合进入H型腔的SPPs谐振能量主要集中在右侧的竖直腔中，通过该侧谐振腔耦合进入透射波导并传输至出射端口，进而显著提升SPPs的透射率并形成图2中的反对称透射峰FR2。当λ=840 nm时，耦合进入H型腔的谐振能量主要集中在左侧的竖腔中，这一部分谐振能量主要与入射波导耦合产生强烈的反射，进而显著降低波导的透射率，形成了FR2右侧的透射极小值。综上可见，FR2的产生主要来源于H型腔结构中两侧竖腔中的一阶谐振(谐振模场分布中仅含有一个波节点)效应。当λ=1 350 nm时，图2中的透射峰FR1相应的模场分布如图3(d)所示，挡板产生的反射波中有一部分能量耦合进入H型谐振腔，并在整个H型腔结构中形成了沿水平方向分布的一阶谐振(波节点出现在横腔中央)，两个竖直腔中收集着极性相反的磁场波腹。右侧竖直腔中的磁场能量将就近耦合进入输出波导并显著提升透射率值，产生透射峰FR1。由模场分布可知，这一透射峰来源于H型腔结构中的水平偶极谐振模式。而当λ<1 350 nm时，由于无法在H型腔中产生谐振，进而入射波导中的能量近乎完全由金属档板反射，显著降低了透射率，形成了FR1左侧的透射阻带。由此可见，图2中的两个Fano透射峰是来源于同一H型腔中的纵向及横向两种不同的谐振模式。

图3 透射峰值与极小值处的模场Hz分布

2 结构参数对透射谱线的影响

首先研究平面结构中横腔长度L1对传感特性的影响，图4所示为模腔长度L1对透射谱线的影响。当选取L2=300 nm，h=150 nm，g=10 nm时，L1以20 nm为步长从100 nm增大到160 nm，其透射谱线如图4(a)所示。随着L1的增大，FR2共振透射峰的中心波长几乎保持不变，而其透射率却随着L1增大而显著降低。这一变化趋势表明FR2透射峰的中心波长主要依赖于竖腔中的谐振模式，进而当L2不改变时，FR2透射峰中心波长几乎不会发生变化。随着L1的增加，H型腔中左右两个竖腔之间的耦合强度必然会发生改变，进而导致透射率急剧下降。因此选择合适的L1值对保持透射峰FR2的透射率具有重要的作用。

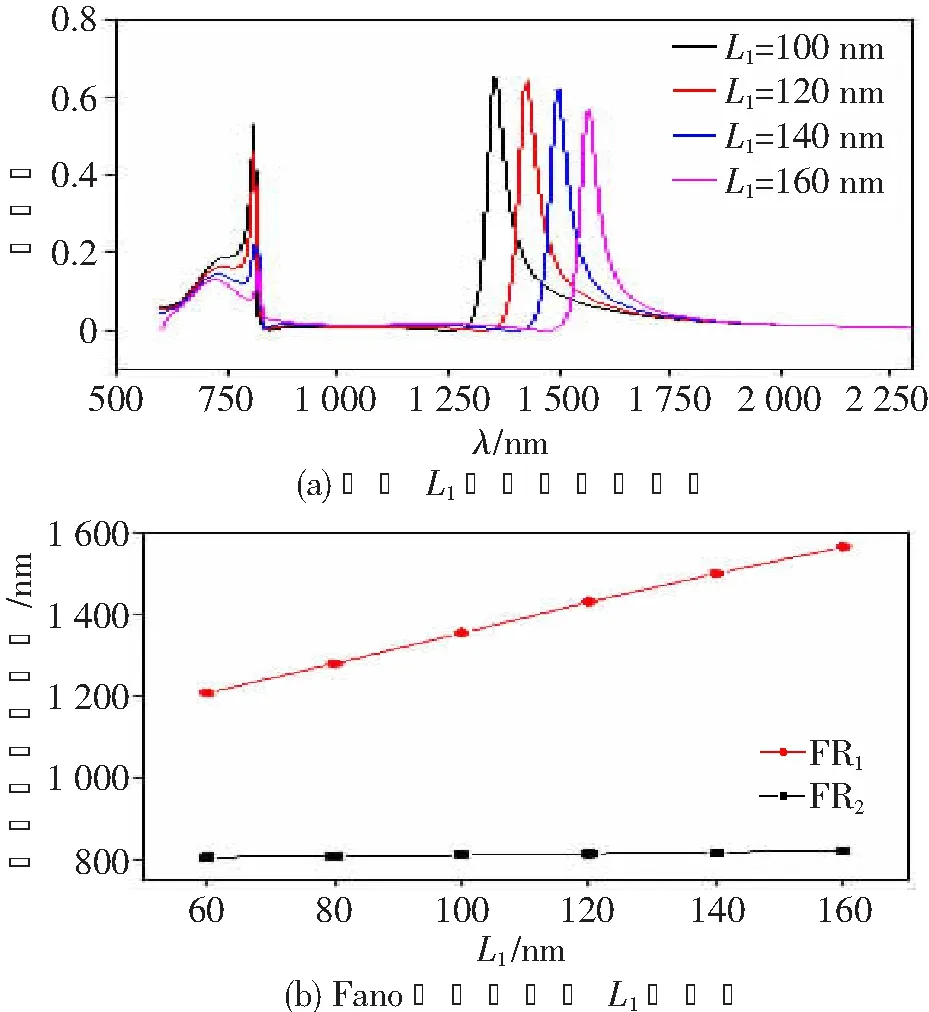
图4 横腔长度L1对透射谱线的影响

对于图4(a)中的另一透射峰FR1，其中心波长却随着L1的增大而发生显著的红移现象。这一结果也与前文讨论的透射峰FR1的产生机理相吻合，由于FR1来源于H型腔中的水平谐振模式，所以L1的增加将导致H型腔水平方向有效腔长Leff的增加。根据式(2)描述的谐振波长与Leff的依赖关系，很容易得到水平谐振模式的谐振波长(即透射峰中心波长)近乎线性增长的变化规律。图4(b)所示为两个透射峰FR2与FR1的中心波长随L1增长的变化规律曲线，FR1共振峰的中心波长随腔长L1线性增加，数值仿真与理论公式的结论相一致。

图5所示为竖腔长度L2对透射谱线的影响。保持横腔长度L1=100 nm不变，以20 nm为步长，将竖腔长度L2的取值从300 nm增大到360 nm。图5(a)所示为两个Fano透射峰都随着L2的增加呈现显著的红移趋势；同时FR2的透射率随着L2的增加也表现出单调递减的变化趋势。这一点再次表明FR2透射峰的形成是基于两个竖腔中的谐振模经由横腔耦合而产生，进而要保证FR2透射峰的透射率，需要L2与L1之间满足一个合适的比例关系。而对于FR1，随着腔长L2的增加，H型谐振腔的等效腔长Leff显然也会随之增大，进而导致水平谐振模式中心波长发生显著红移。两个透射峰中心波长随L2的变化关系如图5(b)所示，随着L2的增长，FR2与FR1的中心波长都呈现单调递增的变化趋势，并且两者之间的波长差值在忽略误差之后主要集中在555 nm附近保持不变。这一特点表明L2的增加对于两个谐振模式的有效腔长的增量贡献接近相等，如图3(a)及3(d)所示。

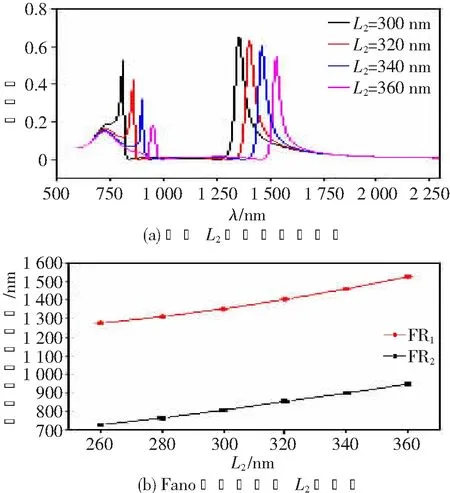
图5 竖腔长度L2对透射谱线的影响

模型结构中横腔的高度参数h分别取60、100和140 nm时，图6所示为不同横腔高度h对透射谱线的影响。谱线图如图6(a)所示。当横腔的高度h偏离竖腔的中心位置上下移动时，FR2与FR1的中心波长都会发生红移。不同的是FR2峰与FR1峰相比红移的幅度较小，在h从100 nm增大到140 nm的过程中，FR2红移范围约为20 nm，而FR1峰的红移幅度达到82 nm。这一现象可以从结构角度找到答案，首先横腔高度的改变显然会影响两竖腔之间的耦合强度，进而在红移FR2的中心波长时也会显著改变其透射率，这一点在图6(a)中得到了印证；另外h取值的变化对于产生FR1峰的谐振模式来说，由于H型腔结构上下对称性的破坏，改变了有效腔长Leff的取值，所以其透射峰中心波长会随横腔的位置而发生显著的改变。图6(b)给出了不同h值对应的两个透射峰的中心波长取值，随着h逐步偏离竖腔的中心位置，两个透射峰FR2与FR1之间的波长间隔会逐渐增加，这是由于FR1峰值波长的红移速度更快所造成的。这个性质也可以用来调整两个透射峰的间距。

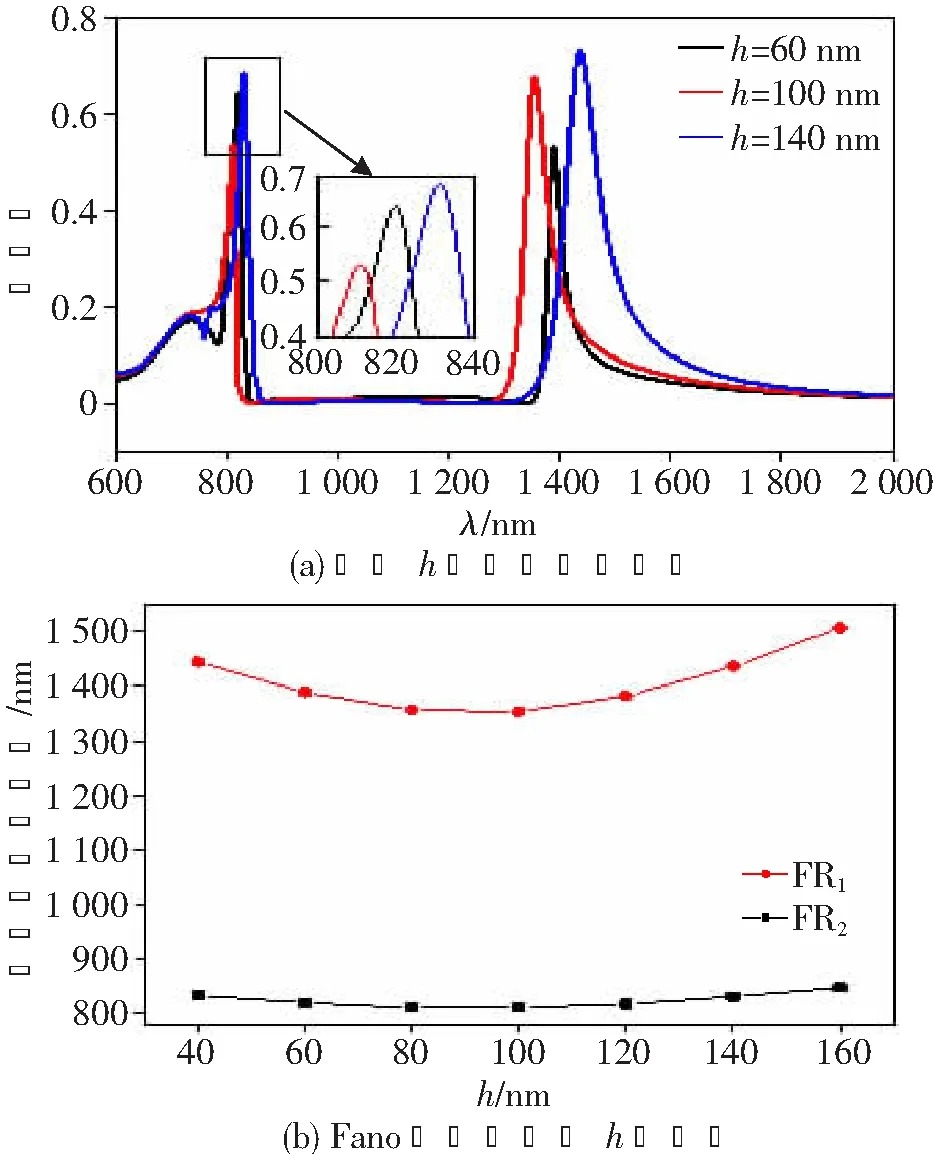
图6 不同横腔高度h对透射谱线的影响

3 传感灵敏度分析

图7所示为不同耦合间距g对透射谱线的影响。固定L1=100 nm，L2=300 nm，h=100 nm，H型腔与主波导之间的耦合间距g以5 nm为步长从5 nm增加到20 nm时，透射谱线如图7所示。由图可见，随着g的增大两个透射峰的峰值透射率是单调下降的，同时透射谱峰呈现蓝移的趋势。显然随着g的增大，波导和谐振腔的耦合强度逐渐减弱，耦合进入谐振腔内部的谐振能量也会逐渐降低，进而导致谐振峰透射率逐步降低；当g减小时，波导和谐振腔的耦合作用也就越明显，腔内的共振能量也会得到加强，耦合进入出射波导的能量也随之增加，进而透射率也随之增大。另外，随着g的增大，透射峰的带宽也不断减小，谱峰的精细度得到提高，这对传感测量的分辨率是极为有利的。综上，模型结构透射谱峰的透射率与精细度是两个此消彼长的物理量，为了在保证透射率的前提下具有较高的分辨率，在模型传感应用中选取g=10 nm。

图7 不同耦合间距g对透射谱线的影响

图8所示为介质折射率与透射谱线及谐振波长的关系。图8(a)所示为H型腔中介质折射率n以0.02为步长从1.00增加到1.10时的透射谱线。图中两透射峰FR2与FR1的中心波长随着折射率的增加都呈现单调递增的红移趋势。图8(b) 所示为峰值波长数值随折射率变化的关系曲线，这里FR2与FR1的中心波长与折射率之间都表现出了近似线性的依赖关系。这一点对于纳米级片上折射率传感的应用极为有利。利用图8(b)中的两条线性拟合曲线的斜率正好可以得到两个透射峰在折射率传感中的灵敏度参数Sλ，其反映的是共振峰漂移

图8 介质折射率与透射谱线及谐振波长的关系

量与折射率改变量的比值，表达式为

式中：Δλ为Fano共振波长的漂移量；Δn为环境变化导致的折射率的改变量。经过对漂移数据的线性拟合可得，FR1和FR2透射峰值折射率传感灵敏度分别约为1 360和750 nm/RIU。

4 结束语

本文引入了尺寸为300 nm×300 nm的H型谐振腔耦合含挡板MDM波导结构实现纳米级折射率传感器的结构设计，并采用有限元法计算了含挡板MDM波导中SPPs模式与H型谐振腔之间的耦合过程。基于H型谐振腔内的两类谐振模式分析了透射谱中双Fano反对称透射峰的产生机理。围绕横向及纵向腔长等结构参数对透射谱线的影响，定量分析了透射峰中心波长及峰值透射率与结构参数的依赖关系。通过改变腔内填充介质的折射率参数得到了透射峰值中心波长与折射率之间的近似线性拟合关系，并计算得到两个透射峰的传感灵敏度分别为750 和1 360 nm/RIU。本文的研究结果为实现易于集成的纳米级折射率传感器提供了参考。