一种改进的压缩采样匹配追踪算法

雷 芳，方泽圣，徐勇军，秦 红，吕京昭

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

多输入多输出(Multi-Input Multi-Output，MIMO)技术通过增加天线数目带来了较高的频谱效率[1]。在结合正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)的大规模MIMO系统中，信道参数的增加为信道估计带来了挑战。线性最小均方误差(Linear Minimum Mean Square Error，LMMSE)算法因其复杂度适中和良好的估计性能被广泛用于无线通信系统中。在稀疏信道下获得良好的估计性能至关重要, 但在大规模MIMO稀疏信道中使用LMMSE算法难以获得较好性能。

传统信道估计算法，如最小二乘 (Least Squares，LS)和最小均方误差(Minimum Mean Square Error, MMSE)算法，必须基于经典的香农采样理论[2]并事先获得信道统计特性，这将导致频谱资源利用率的减少。文献[3]中提出的压缩感知(Compressed Sensing, CS)理论可以用于稀疏信号的恢复，大量实验结果表明信道具有稀疏性[4-5]，因此信道的稀疏性和CS理论可用于获得良好信道估计效果。

大量CS重构算法基于贪婪算法思想，例如正交匹配追踪(Orthogonal Matching Pursuit, OMP)[6]和压缩采样匹配追踪(Compressed Sampling Matching Pursuit,CoSaMP)[7]算法。这类贪婪算法在传感矩阵中寻找与接收信号最相关的列，再通过多次迭代更新残差最后恢复出稀疏信道。但这类贪婪迭代算法的缺点是,在计算残差时所用的LS算法忽略了噪声的影响。本文提出的算法在CoSaMP算法基础上对传感矩阵所选支撑集进行LMMSE估计，最后再进一步进行稀疏信道估计。仿真结果表明，改进后的算法比原算法误码率(Bit Error Ratio,BER)性能提升约1～2 dB。

1 系统模型

考虑一个L条多径的OFDM系统，其单位冲激响应为

式中：t和τ分别为时间和延迟；τq(t)∈R和αq(t)∈

C分别为路径q的延迟和幅度，R和C分别为实数域和复数域；δ为单位冲激响应。假设在持续块衰落信道中，而且忽略符号同步，则离散信道冲激响应为

式中：Tq为采样间隔；L为信道抽头数，即OFDM系统的径数。在L个信道抽头数中有Q(Q≪L)个非零值，称为Q稀疏信道。

考虑M个子载波的OFDM系统，其中包含MP个导频和MD个数据(M=MP+MD)。{X(t1),X(t2),…,X(tMP)}和{Y(t1),Y(t2),…,Y(tMP)}分别为导频位置处的发送符号和接收符号，tMP为第MP个导频所在的位置。导频子载波在频域中估计的传递函数为

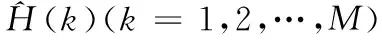
式中：h=[h(1),h(2),…,h(L)]T、X=diag{X(t1),X(t2),…,X(tMP)}和N=[n(1),n(2),…,n(Mp)]T分别为矩阵的单位冲激响应、对角矩阵和高斯白噪声；Y=[Y(t1),Y(t2),…,Y(tMP)]T为接收到的信号矩阵；F为离散傅里叶变换(Discrete Fourier transform, DFT)矩阵，可表示为

式中，w=e-i2π/M，i为虚数单位。

令Ad=XF，由式(4)得：

在信道稀疏大于导频(MP>L)的情况下有助于减少导频，因此可以提高频谱效率。在实际环境中，一般很少有MP=L的情况，在此不做讨论。对于稀疏信道的恢复问题[3]，如果向量h大部分分量等于或接近零(Q≪L)，则存在一个可行的解决方案。

2 CS算法

2.1 CS

CS技术通过使用合适的字典或基，可以用最少数量的非零系数对多个信号进行分类。这种信号可以利用稀疏度的估计和非线性优化进行恢复。由式(5)可知Q稀疏向量h可通过求解I0范数最小化得到[9]：

式中：‖h‖0为h非零项个数；σn为噪声方差。该问题为非确定性多项式难(Nondeterministic Polynomially-Hard, NP-Hard)问题，但可以由凸优化问题替代[4,10]，即转化为

通常这类问题如文献[11]所述，有两类解决方案，即凸优化和贪婪算法[9]。由于凸优化算法并不适合时变信道中的信道估计[12]，且贪婪算法相比凸优化算法具有更低的复杂度，因此本文主要研究贪婪算法。

在一个完整的冗余字典计算信号的最佳非线性估计是通过一个基本的贪婪算法匹配追踪(Matching Pursuit, MP)来实现的。MP通过对信号的逐步筛选，建立了一个最接近矩阵列的线性组合信号。在非正交MP中，测量矩阵在原子间不具有正交性,继续从先前的残差中减去后续的残差，可以重新引入与先前包含原子跨度不正交的成分。因此对于下一次迭代，只考虑留数的正交分量[12]。与传统LS算法相比，MP具有更好的性能。然而，OMP算法的时间复杂度要高于其他贪婪算法，如CoSaMP算法，这是因为其每一步只选择一个原子。因此，本文考虑CoSaMP的改进算法。

2.2 基于LMMSE估计的CoSaMP算法用于信道估计

在CoSaMP算法中，首先选取2Q个原子用于迭代估计。再从2Q个原子中，使用LS算法识别出新的Q维子空间，从而减少了错误的识别。

在传统CoSaMP算法中，求解支撑集的伪逆为

式中：A(LS)为LS 算法下所求支撑集的伪逆；At为每次迭代选出的矩阵A的列集合。

LS算法没考虑噪声的影响，实际通信系统信道中有高斯白噪声的影响。为了改善性能，在算法复杂度和性能之间进行权衡，通常使用LMMSE算法。因此，本文提出了一种基于LMMSE估计的CoSaMP算法。

由式(4)可知，传感矩阵Ad=XF由导频和DFT矩阵构成，每次迭代取其中一列，则均方误差(Mean Square Error, MSE)为

对MSE求关于WH的导数，可得：

式中：Rhh、RhY和RYY分别为h的自相关矩阵、h与Y的互相关矩阵和Y的自相关矩阵；σ和I分别为噪声和单位矩阵。

本文中发送功率为1，为了简化计算，将式(9)和(10)代入式(8)，可得LMMSE估计后的伪逆矩阵A(LMMSE,AWGN)为

式中，SNR为信噪比(Signal-to-Noise Ratio，SNR)。将式(11)代入CoSaMP算法，则改进后的CoSaMP算法如下。以下流程中，rt为残差，t为迭代次数；∅为空集；J0为每次迭代找到的索引；Λt为t次迭代的索引集合；aj为矩阵A的第j列；At为按索引Λt选出的矩阵A的列集合;〈·,·〉为求向量内积;abs[·]为求模值。

输入：接收信号Y,观测矩阵A=XF,稀疏度为Q；

第1步：初始化：r0=Y；Λ0=∅；A0=∅；t=1；

第2步：计算u=abs[ATrt-1](即〈rt-1,aj〉,1≤j≤N)，选择u中2Q个最大值，将这些值对应A的列序号j构成集合J0(列序号集合)；

第3步：令Λt=Λt-1∪J0,At-1=At-1∪aj，j∈J0；

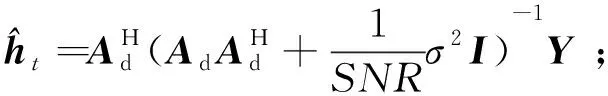
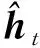
第7步：t=t+1，若t≤Q，则返回第2步继续迭代，若t>Q或残差rt=0，则停止迭代进入第8步；

3 仿真分析

3.1 仿真参数设置

在本节中，使用Matlab仿真平台对本文改进CoSaMP、传统CoSaMP和OMP算法进行仿真验证。导频位置是等间隔导频。信号采用16-正交振幅调制(Quadrature Amplitude Modulation, QAM)调制，信道噪声为高斯白噪声。仿真参数设置如表1所示。

表1 仿真参数设置

3.2 仿真结果分析

本文中，假设已知信道稀疏度为8，即只有8条主径用来传输信号，其他径认为无限接近或等于零。图1所示为信道在时延域的信道响应。CS能够用于信道估计的原因正是因为在第五代移动通信技术(5th Generation Mobile Communication Technolo-gy,5G)中使用的高频段毫米波相比于长期演进(Long Term Evolution, LTE)中低频信号更容易受到环境的干扰，所以在信号传输过程中，只有极少数径能传输信号，这时可认为信道在时延域上表现出稀疏性，因此可以使用CS进行信道估计。

图1 时延域稀疏信道

图2所示为不同信道估计算法的归一化均方误差(Normalized Mean Squared Error, NMSE)随着SNR的变化关系。由图可知，在低SNR的情况下，改进后的LMMSE-CoSaMP算法性能优于CoSaMP算法。在SNR=5 dB时，LMMSE-CoSaMP算法的NMSE相比于CoSaMP算法约有2 dB的性能提升。整体性能提升在低SNR时要好于高SNR时。这是由于LMMSE-CoSaMP算法在迭代过程中，对从传感矩阵中取出的相关列进行了LMMSE估计，可近似看成在CoSaMP算法的基础上增加了一个维纳滤波器，减小了噪声对系统的影响。随着SNR的提高，噪声对系统的影响随之降低，使得LMMSE-CoSaMP算法的性能逐渐接近CoSaMP算法的性能。相比于LMMSE算法， LMMSE-CoSaMP算法复杂度略高，但算法中只对少量K列进行LMMSE估计，而相比于在性能上带来的提升，增加的算法复杂度可接受。

图2 不同算法的NMSE随SNR的变化关系

图3所示为不同算法的BER随SNR的变化关系，当SNR=5 dB时，LMMSE-CoSaMP算法相比于CoSaMP算法的BER降低了约34.7%。当BER=10-1时，LMMSE-CoSaMP算法相比于CoSaMP算法的性能提升了约2 dB。在理论上，本文的LMMSE-CoSaMP算法相比于CS理论的CoSaMP算法取得了更好的系统性能。图4所示为不同算法的NMSE随导频数量的变化关系。相比于传统的LMMSE算法，在具有相同系统性能时，LMMSE-CoSaMP算法使用更少的导频，有效解决了5G 大规模MIMO系统中带来的导频污染。

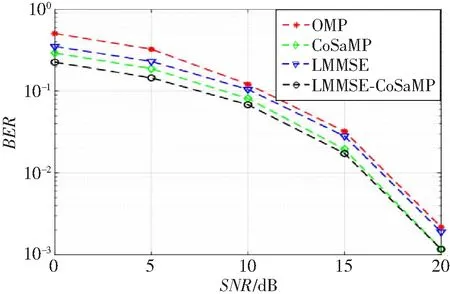
图3 不同算法的BER随SNR的变化关系

图4 不同算法的NMSE随导频数量变化的关系

4 结束语

本文提出了一种OFDM系统中的信道估计算法，该算法结合了传统的CS重构CoSaMP和LMMSE算法。利用信道在延迟域上的稀疏特性，基于先验支撑集对稀疏信道进行重构。传统CS重构算法中贪婪迭代算法是通过LS更新残差，没有考虑噪声影响。通过对支撑集进行LMMSE估计，降低了噪声对系统的影响。相比于传统CoSaMP算法，LMMSE-CoSaMP算法在低SNR时，BER提升约1～2 dB，具有更好的抗噪声性能。因此其他贪婪迭代算法也可以结合LMMSE估计以获取更好系统性能，同时还有效减少了导频开销。