基于经验模式分解与纵横交叉算法的台区负荷预测

白格平，李英俊，付 宁，朱生荣

(1.内蒙古电力(集团)有限责任公司，内蒙古 呼和浩特 010020；2.乌兰察布电业局，内蒙古 乌兰察布 012000)

0 引言

为了帮助电力企业制定更优的电力调度方案，需要准确地预测短期电力负荷。精准的负荷预测对电力系统的稳定运行起着至关重要的作用[1]。随着经济的发展和人们生活水平的提高，用电需求不断提升，以致整个电网的用电负荷将不可避免地增长。2020年，用电负荷会达到6.8～7.2万亿千瓦时，电能会占总能源消费的27%[2]。为了实现高精度的负荷预测，越来越多的算法被提出。

迄今，国内外学者主要采用回归分析法、时间序列法、灰色模型法和人工智能方法这4种预测方法对负荷进行预测。负荷的变化存在许多影响因素。回归分析法[3]就是建立负荷与这些因素的回归关系，再进行预测。但回归分析法的建模能力有限，无法良好地适用于存在众多影响因素的现代电力系统。时间序列法[4]假设用电量变化是连续且变化平缓的，通过对以往的用电量进行统计并分析，从而建立预测模型。但对于冲击性负荷这种波动激烈的负荷，时间序列法的预测精度难以令人满意。灰色模型法[5]能将随机过程量化为一定变化范围的灰色量，通过研究其历史数据的规律实现对负荷序列的预测。

由于人工智能方法对非线性和不确定性的时间序列拟合能力强大[6]，国内外研究人员近年来尝试将其应用于负荷预测中。这些方法包括人工神经网络(artificial neural network，ANN)、支持向量机(support vector machine，SVM)和极限学习机(extreme learning machine，ELM)等。ELM由于其更快的训练速度和预测性能而备受研究人员青睐。ELM的机制规定输入权值和中间层阈值的生成是不定的，造成模型的预测性、可靠性较差。文献[7]提出一种改进型的粒子群算法，并将其优化ELM参数。试验结果证明，其预测效果比单一的ELM和径向基神经网络更好。文献[8]提出一种基于改进型遗传算法优化ELM的负荷预测模型。试验结果证明，改进模型具有更快的训练速度，并适用于现代电力负荷预测。因此，通过与智能优化算法结合，ELM的预测可靠性可以进一步提升。

各类电力电子器件的应用，以及国家鼓励风电、光伏发电等清洁电力的并网使用，导致电网出现了大量的冲击性负荷，为负荷预测带来困难。通过结合模式分解算法和人工智能预测方法的混合模型，可以有效地处理原始负荷序列和拟合历史数据之间的非线性关系，从而大大降低预测难度。例如，文献[9]采用变分模式分解(variational mode decomposition，VMD)将历史负荷序列分解，以用不同的ELM对每一条子序列进行预测，并对它们的ELM预测值进行求和。试验结果显示，利用模式分解可以明显增强预测准确性。文献[10]采用样本熵 (sample entropy,SE) 值作为评判标准：首先，通过VMD将原始负荷序列进行分解；然后，根据每个子序列的SE值进行模态重构；最后，采用Elman神经网络建模。这也再次证明了利用模式分解将原始负荷序列分解的模型预测性能更好。

为了更好地预测冲击性负荷，本文提出了一种基于经验模式分解(empirical mode decomposition,EMD)和纵横交叉优化(crisscross optimization,CSO)算法的ELM的短期台区负荷预测模型，即EMD-CSO-ELM混合预测模型。为了降低冲击性负荷预测难度并保留其有效信息：首先，使用EMD将负荷分解成一系列相对平稳的子序列；然后，为了提高ELM的泛化性能，使用CSO算法的ELM对每个模态分量建模；最后，将预测结果叠加并得到预测值。本文采用某台区的用电数据搭建模型，对工作日和休息日的用电量进行预测，并和其他模型作对比分析。根据试验结果，本文提出的EMD-CSO-ELM混合预测模型在预测精度和收敛速度方面明显优于其他对比模型。

1 混合预测模型及误差指标

1.1 EMD-CSO-ELM混合预测模型

本文仿真所用负荷来源于广东某台区的实测电量数据，以15 min的平均值为一个观测值，每天共有96个观测值。某台区典型日和连续一周负荷如图1所示。由于存在大量冲击负荷，从图1可以看出负荷曲线有很多毛刺。

图1 某台区典型日和连续一周负荷Fig.1 Typical daily and weekly load of a transformer area

EMD-CSO-ELM台区负荷预测模型流程如图2所示。

图2 EMD-CSO-ELM台区负荷预测模型流程图Fig.2 EMD-CSO-ELM load forecasting model flowchartof transformer areas

1.2 误差指标

采用如式(1)所示平均绝对误差(mean absolute error，MAE)和式(2)所示均方根误差(root mean square error，RMSE)，对模型的预测效果进行评价。

(1)

(2)

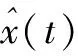
2 经验模式分解

EMD是一种经验信号处理算法，主要用于提取非线性数据的特征。由于台区负荷序列是冲击性序列，使用EMD将负荷序列进行分解后再进行预测可以提升预测精度。EMD的计算步骤可以描述如下。

①确定所有关于负荷数据的局部极值。

②通过连接最大点，借助三次样条插值函数得到原数据的上包络线XU(t)；利用同样的方法，通过连接最小点，得到原数据的下包络线XL(t)。

③均值包络线M(t)的表达式为：

(3)

④新的Y(t)(数据序列)为：

Y(t)=X(t)-M(t)

(4)

式中：X(t)为原数据序列；M(t)为均值包络线。

若该中间信号同时满足本征模函数(intrinsic mode function,IMF)的条件，则该信号为IMF的一个分量并设其为C(t)=Y(t)；否则，将X(t)信号替换为Y(t)，重新作步骤①～步骤④的分析。IMF分量的获取通常需要若干次的迭代。

⑤计算剩余量R(t)：

R(t)=X(t)-C(t)

(5)

将X(t)替换为R(t)，并重复步骤①～步骤⑤，直至所有的IMF分量都找到。

最后，风电数据(或风速数据)可表示为：

(6)

负荷序列的EMD结果如图3所示。

图3 负荷序列的EMD结果Fig.3 EMD results of load sequence

3 CSO算法优化的ELM

3.1 极限学习机

(7)

式中：wk=[wk1wk2…wkn]T;β为输出权系数矩阵,β= [βk1βk2…βkm]T;bk为第k个隐含神经元的位置(bias)。

式(7)表示的N条公式可以表示为：

Hβ=T

(8)

(9)

式中：H为隐含层输出权系数矩阵;T为目标矩阵；g()为Sigmoid激活函数。

(10)

与其他算法相比，因ELM输入权重和隐含层阈值是随机生成的，其H会一直保持不变。因此，训练ELM的过程就相当于找到β=H+T的最小二乘解，即：

β=H+T

(11)

式中：H+为H的Moore-Penrose广义逆矩阵。

考虑到输入权系数和隐含层阈值对ELM预测效果的重要性，本研究采用CSO方法建立CSO-ELM预测模型。

3.2 CSO算法

不同于诸如粒子群优化(particle swarm optimization,PSO)算法这样的群智能优化算法，CSO[11]拥有两种独特的交叉算子，分别为横向交叉和纵向交叉，从而形成一种有别于其他优化算法的双向搜索竞争机制，可以很好地提升局部最优搜索能力，即可跳出局部最优继续寻找全局最优。在双向搜索的竞争方式下，CSO在每次的迭代过程中都产生被称为中庸解的子代，随后通过贪婪的选择机制比较中庸解和父代，将获胜的解称为占优解，并将其替换成父代。

①横向交叉。

假设对粒子X(i)和X(j)的第d维交叉，即：

(12)

式中：r1、r2为[0,1]上的随机数;c1、c2为[-1,1]上的随机数；Xid和Xjd分别为粒子X(i)和X(j)的第d维；Mid和Mjd分别为横向交叉后的第d维子代。

②纵向交叉。

纵向交叉是通过对1个粒子不同的2个维度进行交叉更新。假设第d1维和第d2维进行交叉，公式如下：

Mi,d1=rXi,d1+(1-r)Xi,d2,i∈(1,M),

d1,d2∈(1,D)

(13)

式中：M为粒子的个数;D为粒子的维数;r为[0,1]上的随机数；Mi,d1为粒子X(i)的第d1维子代。

3.3 CSO-ELM模型

由于ELM的输出权重是根据输入权重和隐藏层阈值来计算的，因此不可避免地存在一些非最佳的输入权重和隐藏层阈值。这可能导致ELM的泛化性能变差。为了解决上述问题，本文根据式(14)，利用CSO优化ELM的参数选择提升ELM的预测精度。

目标函数为：

(14)

4 模型参数选定

有3个参数将会影响所提出模型的预测性能，分别是ELM隐藏神经元个数、EMD分解层数和纵向交叉概率。本节将通过3组试验，分别确定这3个参数。

4.1 ELM隐藏层神经元个数确定

根据文献[12]，ELM隐含层神经元的个数可由式(15)确定：

(15)

式中：L为隐藏层的维度;m为输入层的维度;n为输出层的维度。

在以下试验中，隐藏层神经元个数都设置为10。

4.2 EMD分解层数确定

由于冲击性负荷的稳定性差，增大了预测的难度，本文采用EMD对负荷进行分解，但需要进一步确定分解的序列数，以获得更好的预测精度。本小节使用EMD-CSO-ELM研究一次模式分解的最佳分解次数。试验将分解次数设置为2～9次。

EMD-CSO-ELM预测误差与EMD分解层数关系如图4所示。

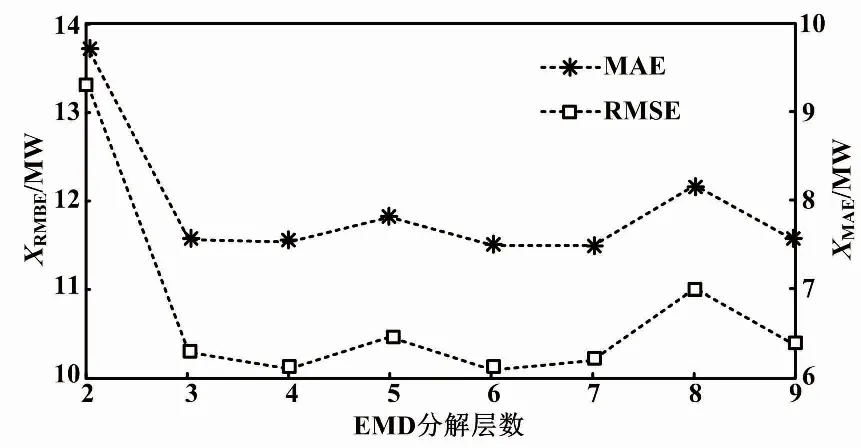
图4 EMD-CSO-ELM预测误差与EMD分解层数的关系Fig.4 Relationship between EMD-CSO-ELM prediction errorand EMD decomposition layers

从图4可以看出，将原始序列分解成6个子序列时，预测误差最小。因此，在以下案例研究中将EMD的分解层数统一设置为6。

4.3 纵向交叉概率确定

与其他群智能优化算法对比，CSO更易于实现，并且仅需要调整纵横交叉概率Pv即可。为了研究不同Pv对CSO性能的影响，本小节使用不同Pv进行试验，并确定其值。

EMD-CSO-ELM预测误差与Pv的变化如图5所示。

图5 EMD-CSO-ELM预测误差与Pv的关系Fig.5 Relationship between EMD-CSO-ELM predictionerror and Pv

从图5可以看出，将Pv设置为0.4时，预测性能最好。因此，在以下算例分析中，将Pv统一设置为0.4。

5 算例分析

5.1 EMD有效性验证

为了验证EMD可以降低预测难度并提升预测精度，本文选取不采用EMD的预测模型与采用EMD的预测模型进行对比分析。不同模型的预测误差如表1所示。

从表1可以看出，无论基准模型是ELM、BP或Elman，使用了模式分解的模型预测误差更低。以ELM为例:EMD-ELM与ELM相比，XMAE在工作日、休息日预测中分别降低了28.77%、26.88%；EMD-ELM与ELM的相比，XRMSE在预测中降低了41.52%、34.98%。试验结果证明，利用EMD的预测模型分解负荷序列可以提升预测精度，即EMD是有效的。

表1 不同模型的预测误差对比

5.2 CSO有效性验证

尽管EMD-ELM的预测性能比ELM好，但仍可以进一步提高预测精度。这是因为ELM性能还取决于其输入权重和隐藏层偏置的调整。

本小节除了将所提出的CSO用于优化EMD-ELM外，还采用PSO算法、遗传算法(genetic algorithm，GA)和差分进化(differential evolution，DE)算法优化EMD-ELM。不同优化算法优化EMD-ELM的预测误差如表2所示。

表2 不同优化算法优化EMD-ELM的预测误差对比

从表2所示的不同优化算法EMD-ELM的预测误差对比，可以得出以下结论。

①与群智能优化算法结合的模型，其收敛精度明显提高了，预测精度也有大幅的提升。以EMD-ELM和EMD-CSO-ELM为例，EMD-CSO-ELM与EMD-ELM相比，XMAE在工作日、休息日预测中分别降低了31.86%、39.24%；EMD-CSO-ELM与EMD-ELM相比，XRMSE在工作日、休息日预测中分别降低了26.55%、29.19%。

②EMD-CSO-ELM无论在工作日还是在休息日的预测中，使用其他群智能优化算法优化的模型中XMAE与XRMSE都更小。这表明CSO克服了局部最优的现象，具有普遍性和适用性，也体现了EMD-CSO-ELM的预测效果，适用于台区负荷预测。

不同模型预测结果如图6所示。

图6 不同模型预测结果Fig.6 Prediction results of different models

6 结论

本文提出了一种利用EMD分解冲击性负荷，并使用CSO算法优化的ELM对分解后子序列建模的台区负荷预测模型。为降低冲击性负荷在预测中带来的负面影响，所提出的EMD-CSO-ELM混合预测模型利用EMD将原始冲击台区的负荷序列分解成更平稳的子序列，并使用CSO算法优化ELM。与其他优化算法相比，CSO可以进一步提高预测精度。EMD-CSO-ELM具有优良的预测性能，应用前景广阔。