基于EWT-OPRCMDE-ELM的风电机组齿轮箱故障诊断研究

李 辉,李 宣,贾 嵘,罗兴琦,白 亮

(1.西安理工大学电气工程学院，陕西 西安 710048；2.西安理工大学水利水电学院，陕西 西安 710048)

0 引言

恶劣的工作环境导致风机故障频发[1]。齿轮箱作为风电机组传动系统的主要设备，更是故障的高发部位。据统计，齿轮箱故障占机组总故障60%以上[2]，而一台风力机故障停机时间的20%是由齿轮箱故障引起的。一旦发生故障，机组将面临长时间停机和昂贵的维修费用，损失巨大[3]。因此，准确、高效地对风机齿轮箱进行故障诊断，对于保障机组的安全、稳定运行具有重要意义。

由于齿轮箱故障振动信号受背景噪声、交变载荷和传输路径等影响，呈现非平稳、非线性的特点，通常用时频分析方法对其处理，如小波变换、经验模态分解(empirical mode decomposition,EMD)、变分模态分解(variational mode decomposition,VMD)等。但是小波变换中小波基的选择不当会对处理效果产生不良影响。EMD方法缺乏理论基础且存在模态混叠、端点效应等问题，所以无法有效分析故障信号。VMD方法依赖于分解层数和惩罚因子的设定，如参数设置不当，将极大地影响地处理效果。针对传统信号处理方法的不足，Gilles[4]结合经验模态分解的自适应性和小波分析的框架理论，提出了经验小波变换(empirical wavelet transform,EWT)方法,有效地改善了传统时频分析方法的弊端。文献[5]将EWT应用于旋转机械故障诊断中，并证明EWT处理效果优于传统EMD方法。

高效地提取区分度大的稳定特征是风电机组齿轮箱故障诊断的重要环节。学者们通常提取故障信号的时域、频域或时频域特征，进行故障诊断。文献[6]提取轴承振动信号的均值、峭度等时域特征，进行故障诊断，取得较好的诊断效果。文献[7]提取轴承振动信号的时域、频域和时频域的多个混合特征参量，利用XGBoost进行风机轴承故障诊断。文献[8]融合风机齿轮箱振动信号的时域、频域和时频域特征，特征降维后利用随机森林算法进行故障模式识别。但是，由于振动信号受强烈噪声干扰、多振动源耦合和传输路径等影响，导致基于传统时域、频域和时频域特征提取的故障诊断方法效果不佳，故障诊断正确率和诊断时间受特征参量的维数影响较大。精细复合多尺度散布熵[9](refined composite multi-scale dispersion entropy,RCMDE)作为一种衡量时间序列复杂度的非线性动力学参数，已被成功应用于心电信号和脑电信号的分析中，并被证明在计算速度和稳定性方面优于样本熵和排列熵。其特征提取效果优于传统时域、频域特征。

极限学习机(extreme learning machine,ELM)[10]是一种泛化的单隐层前馈神经网络的机器学习算法。其输入层和隐含层之间的连接权值和隐含层阈值随机产生，训练过程无需迭代调整，与传统反向传播(back propagation,BP)神经网络、支持向量机等智能分类算法相比，输入参数少、运算速度更快。

为提高风电机组齿轮箱故障诊断效果，本文提出一种基于EWT重构、最优参数精细复合多尺度散布熵和ELM结合的故障诊断方法，并将其应用于风电机组齿轮箱。

1 经验小波变换

EWT是通过对信号的傅里叶频谱进行自适应分割，根据分割边界，构建正交小波滤波器组以提取包含故障信息的调幅调频分量。步骤如下。

①对故障信号进行傅里叶变换，将信号的傅里叶频谱定义在[0，π]范围内，并将[0，π]分成N个带宽不等的频带，则每个频带可以表示为Λn=[ωn-1,ωn]。以ωn为中心，定义Tn=2τn为过渡带。傅里叶轴分割如图1所示。

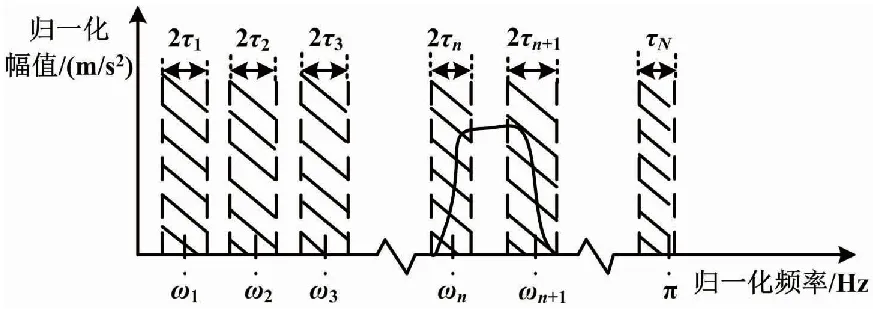
图1 傅里叶轴分割Fig.1 Partitioning of the Fourier axis

②经验小波的尺度函数φn(ω)和小波函数ψn(ω)在频域里的计算式如下：

(1)

(2)

③根据经典小波变换的方法构造经验小波变换，细节系数由经验小波函数内积计算得出，近似系数由经验尺度函数内积计算得出：

(3)

(4)

原信号重构表达式如下：

(5)

式中：∧表示傅里叶变换;∨表示傅里叶逆变换;—表示复共轭;⊗表示卷积。

经验模态fk(t)定义如下：

(6)

2 精细复合多尺度散布熵

散布熵计算步骤如下。

①x={xj|j=1,2,…,N}为一时间序列，利用正态分布函数将时间序列x映射到y={yj|j=1,2,…,N}，yj∈(0,1)，即：

(7)

式中：μ、σ分别为期望和标准差。

②通过线性变换将y映射到{1,2，…，c}范围内：

(8)

(9)

式中：m、d分别为嵌入维数和时延。

④计算散布模式πv0v1…vm-1，v=1,2,…,c。

(10)

⑤计算每种散布模式的概率πv0v1…vm-1：

(11)

⑥根据香农熵定义,有：

(12)

散步熵(dispersion entropy,DE)的值越大，信号时间序列不规则程度越高；反之，不规则程度越低。

RCMDE计算步骤如下。

RCMDE是对原始数据精细化和多尺度化，其作用是减小初始点位置对计算结果的影响和充分利用数据序列的信息。计算过程如下。当尺度因子为S时：首先，将原始信号按初始点连续分割成长度为S的小段，求取每一段的平均值，再将这些平均值按顺序排列成S个粗粒化序列；其次，计算每个粗粒化序列散布模式π的概率，并计算这些散布模式概率的平均值；最后，根据香农熵的定义计算RCMDE的值。

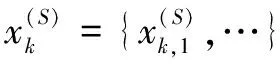
(13)

②对于每个尺度S，RCMDE值定义如下：

(14)

3 Relief-F与ELM

提取齿轮箱故障特征后，由于存在特征冗余，会使诊断时长和精度受影响。故采用Relief-F算法[11]计算分类权重，剔除冗余。Relief-F算法是从Relief算法扩展而来的，可以处理多类别分类权重问题。该算法计算过程如下。

①从所有样本中，随机取出一个样本a。

②在与样本a相同分类的样本组内，取出k个最近邻样本。

③在所有其他与样本a不同分类的样本组内， 也分别取出k个最近邻样本。

④计算每个特征的权重。

极限学习机是一种单隐层前馈神经网络，由输入层、隐含层和输出层构成。与传统神经网络不同的是，极限学习机的输入层与隐含层之间的连接权值和隐含层神经元的阈值为随机设定，在开始创建网络时随机产生，且设置完成后无需调整。隐含层与输出层之间的连接权值由方程组依次解出，无需迭代计算。故极限学习机可在保证学习精度的前提下极大地加快学习速度。

极限学习机训练过程如下。假设有N个任意样本(Xi,ti)。其中，Xi=[xi1xi2…xin]T∈Rn，ti=[ti1ti2…tin]∈Rm，n为输入层的维度，m为输出层的维度。

当隐层节点的个数为L时，单隐层前馈神经网络输出可以表示为：

(15)

式中：i=1,2,…,N;Wj=[wj1wj2…wjn]T为输入权值;βj=[βj1βj2…βjm]T为输出权重;bj是第j个隐层单元的偏置;WjXj为Wj与Xj的内积;g()为激活函数。

单隐层前馈神经网络学习的目标是在最小的误差下逼近N个样本，可以表示为：

(16)

即存在Wj、βj、bj，使得：

(17)

式(17)可简化为Hβ=T。其中：H为隐层节点输出矩阵；β为输出权重；T为期望输出。

(18)

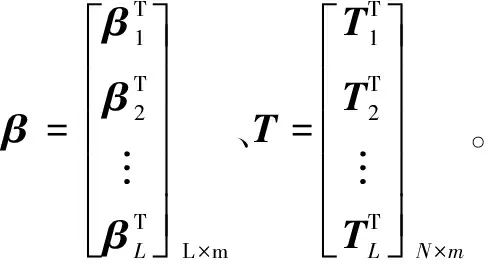
1,2,…,L

(19)

当输入权重Wj和隐含层偏置bj随机确定后，隐层的输出矩阵H就会被确定。此时，单隐层神经网络求解的问题被转换成线性系统Hβ=T的求解，则输出权重β可由式(20)确定。

(20)

极限学习机诊断过程如下。

①设定激活函数g()和隐层神经元个数N。

②输入训练集进行网络训练。

③利用训练好的ELM，输入测试集进行故障诊断。

4 故障诊断流程

故障诊断流程如下。

①利用振动传感器采集风电机组齿轮箱轴承故障振动信号。

②利用EWT分解原始振动信号，将得到若干子模态分量EWF。

③计算各子模态分量与原始信号的相关系数Rn。设定相关系数阈值为0.3，选取大于阈值的子模态分量EWF进行信号重构，提取故障主要信息。

相关系数是一种度量2个反映之间相关程度的系数，其值介于1和-1之间。其中：1表示变量完全正相关；0表示无关；-1表示完全负相关。皮尔逊相关系数定义为两个变量之间的协方差和标准差的商。函数表达式为：

(21)

④以重构信号RCMDE偏度值的平方函数为适应度函数，计算重构信号最优RCMDE参数，提取重构信号最优参数RCMDE(optimal parameter RCMDE,OPRCMDE)构成故障特征向量。

⑤利用Relief-F计算OPRCMDE各尺度特征分类权重，并进行特征参量筛选，剔除冗余特征。

⑥将筛选得到的特征向量作为输入，利用ELM进行故障诊断。

5 信号仿真验证

为验证EWT分解在处理复杂信号时的优越性。采用仿真信号进行验证。仿真信号f由指数信号f1、调频信号f2、噪声信号f3(强度为0.2 dB·W)构成。仿真信号时域如图2所示。

图2 仿真信号时域图Fig.2 Time domain diagram of simulation signal

利用EWT分解信号f，同时与EMD方法对比。EWT分解结果时域如图3所示。EWT分解结果的Hilbert谱如图4所示。

图3 EWT分解结果时域图Fig.3 Time domain diagram of EWT decomposition results

图4 EWT分解结果的Hilbert谱图Fig.4 Hilbert spectrum of EWT decomposition results

(22)

根据图3和图4，由 EWT分解结果可得，EWT将模拟信号f分解为4个子模态分量。 其中，EWF1在[0,1]上单调增加，最大值为5，对应于f1的变化趋势。 EWF2的周期约为0.1 s，其波形和周期对应于f2中的sin(20πt)。而EWF3的周期约为0.05 s，对应于f2中cos(40πt)。 EWF4没有明显的特征，并且在时域中很杂乱，因此被判断为噪声信号。 同时，在Hilbert频谱中可以观察到清晰、稳定的10 Hz和20 Hz对应于f2的特征频率。EMD分解结果时域如图5所示。

图5 EMD分解结果时域图Fig.5 Time domain diagram of EMD decomposition results

EMD分解结果的Hilbert谱图如图6所示。观察图5和图6，EMD将模拟信号分解为8个子模态分量，但只有Res分量具有与其相同的变化趋势，并且很难清楚地观察到其余IMF分量中与模拟信号分量相对应的分量。 而且，由于噪声干扰，Hilbert频谱中的特征频率不规律且杂乱混叠，并且难以观察到稳定的模拟信号中包含的特征频率。

图6 EMD分解结果的Hilbert谱图Fig.6 Hilbert spectrum of EMD decomposition results

上述仿真试验中，通过比较EWT和EMD的分解结果，可以发现EMD方法会过度分解信号，并且存在模态混叠现象，不能有效地提取故障特征分量。 EWT可以在嘈杂的环境中有效地提取信号的主要成分，以获得更好的特征提取结果。

6 试验分析

本节结合了EWT信号重构和OPRCMDE，并使用极限学习机进行故障诊断。采用基于千鹏 QPZZ-Ⅱ 旋转机械振动及故障模拟试验平台的齿轮箱振动数据进行分析。试验平台由变速驱动电机(0.75 kW)、轴承、齿轮箱、轴、偏重转盘、调速器等组成。通过调节配重、调节部分的安装位置以及组件的有机组合，快速模拟各种齿轮箱故障。

齿轮箱参数如下。

①齿轮。大齿轮：模数2、齿数75、材质S45C(3只，其中2只备件齿轮)；小齿轮：模数2、齿数55、材质S45C(2只，其中1只备件齿轮)。

②润滑：浸油式。

③轴承：滚动轴承(N205)。

设定转速为880 r/min，采样频率为5 120 Hz，通过安装在齿轮箱输出轴负载侧轴承X方向的加速度传感器，采集齿轮箱正常、点蚀、磨损和断齿这4类故障状态的振动信号各25组样本。每个样本长度为2 048。

6.1 EWT分解与重构

以齿轮箱齿轮磨损故障为例。EWT将磨损故障信号分解为10个EWF。根据本文所提到的相关系数阈值，选取EWF2、EWF6为最优分量重构故障信号并进行下一步的故障特征提取及模式识别。

EWF相关系数如图7所示。

图7 EWF相关系数Fig.7 Correlation coefficient of EWF

6.2 OPRCMDE参数计算及特征提取

选取合适的RCMDE参数，能够有效提取区分度较大的故障特征向量，同时减少计算时间。针对不同的故障类型选取对应的最佳参数，可获取最佳的故障特征区分度。

在精细复合多尺度散布熵的计算中，涉及4个参数的选取，即尺度因子S、嵌入维数m、类别个数C和时延d。为充分利用轴承故障数据，设置尺度因子S=15，时延d对算法影响较小，故设置为1。嵌入维数m、类别个数C的设定对特征提取效果影响重大。m过大，将导致RCMDE运算时间加长；m过小，则算法检测信号突变性减弱。C过大，将导致RCMDE对噪声十分敏感；C过小，则彼此相距较远的两个振幅可能被分到相同的类别内。考虑到m和C之间的交互作用，使用网格搜索算法对范围内的最优m值和C值进行同步搜索。

为分析多尺度熵值的集中趋势，可计算其均值。但仅凭均值不足以表征多尺度熵值的总体趋势。本文引入精细复合多尺度散布熵的偏度。其绝对值越大，表明均值的效能越有问题；其绝对值越小，表明均值越可信赖。本文以EWT重构信号精细复合多尺度散布熵偏度的平方函数[12]作为适应度函数，求取其最小值。偏度计算过程如下：

信号序列X={xi},i=1,2,…,N。15个尺度下的精细复合多尺度散布熵值组成序列：

BP(X)={BP(1),BP(2),…,BP(15)}

(23)

偏度值为：

(24)

适应度函数取为：

(25)

设定m搜索范围为[2,6]、C搜索范围为[3,8]、设定步长均为1。通过网格搜索算法，得到4类故障OPRCMDE参数，如表1所示。

表1 4类故障OPRCMDE参数

提取4类故障状态EWT重构信号的OPRCMDE值，得到4组25×15故障特征矩阵。原始信号推荐参数RCMDE如图8所示(4类故障状态均设定m=3、C=6)。EWT重构信号OPRCMDE如图9所示。

图8 原始信号推荐参数RCMDEFig.8 RCMDE of recommended parameters of original signal

图9 EWT重构信号OPRCMDEFig.9 OPRCMDE of the EWT reconstructed signal

对比图8、图9，可观察到本文方法所提取的4种故障状态特征区别明显，有利于后期的故障特征提取和故障诊断。

由于高维OPRCMDE特征向量存在冗余，利用Relief-F算法(参数设置迭代次数M=20,近邻值KL=5)计算每个尺度因子下OPRCMDE值的特征权重，并进行特征向量二次筛选和约简。各尺度因子分类特征权重如图10所示。

图10 各尺度因子分类特征权重Fig.10 Feature weights at each scale

根据权重大小，选取第1、第2、第6共3个尺度因子下的OPRCMDE值作为故障特征向量，约简后得到4组25×3的故障特征矩阵。Relief-F约简特征散点图如图11所示。观察图11可发现：各类故障间聚集紧密从而可将4种不同故障状态明显地区分开。

图11 Relief-F约简特征散点图Fig.11 Relief-F reduced feature scatter

6.3 极限学习机故障诊断

为4故障状态贴上标签，正常、点蚀、磨损、断齿的标签分别为1、2、3、4。选取60%样本作为训练样本，剩余40%样本作为测试样本。测试集40个样本分类结果与实际类别一致，故障诊断正确率100%，对应类别未出现错误分类。ELM诊断结果如图12所示。

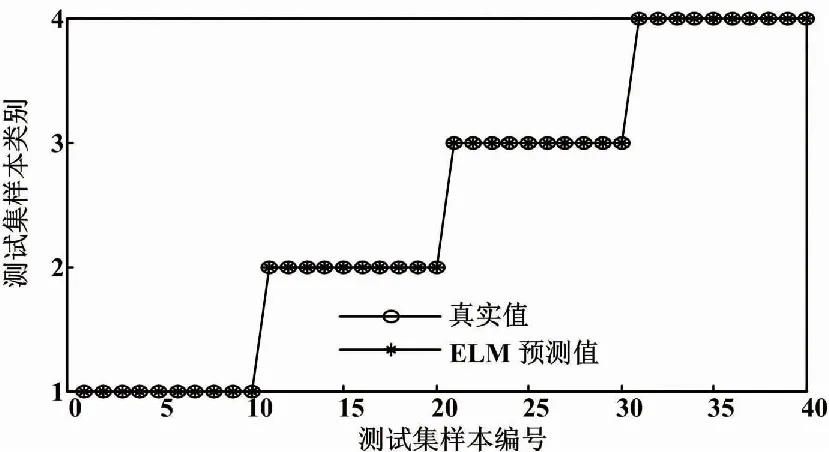
图12 ELM诊断结果Fig.12 Results of ELM diagnosis

根据试验结果，证明本文提出的方法能够提取风机齿轮箱区分度较大的故障特征，实现了对齿轮箱不同故障的准确诊断。为进一步说明本文方法的优越性，将本文方法与多尺度排列熵(multi-scale permutation entropy,MPE)-ELM(MPE参数设置为m=5、S=12、T=1)、MPE-ReliefF-ELM、RCMDE-ELM(RCMDE参数推荐设置为m=3、C=6)、时频域融合特征-ReliefF-ELM(时频域融合特征共11个，其中8个时域特征分别为平均值、有效值、峰值、峰值因子、峭度、波形因子、脉冲因子、裕度因子，3个频域特征分别为重心频率、均方频率、频率方差)进行对比。每种方法运行10次，取诊断正确率平均值。各诊断模型诊断效果对比如表2所示。

表2 各诊断模型诊断效果对比

由表2中结果可知，当本文方法所提取的齿轮箱故障特征应用于齿轮箱故障诊断时，诊断准确率更高且更加稳定。

7 结论

本文针对传统风电机组齿轮箱故障诊断方法的不足，提出一种基于EWT重构、最优参数精细复合多尺度散布熵和极限学习机结合的故障诊断方法。具体结论如下。

①EWT解决了传统时频处理方法存在的模态混叠、端点效应、参数设置等问题。通过相关系数选取子模态分量进行信号重构，提取了故障的主要信息。

②为提高精细多尺度散布熵算法的特征提取性能，以其偏度值的平方函数作为适应度函数，通过网格搜索算法同步搜索计算2个关键参数(即m和C)。通过试验对比，证明EWT重构信号最优参数精细复合多尺度散布熵在提取各类故障特征时区分度更好，诊断结果更稳定准确。

③针对特征向量冗余和一般分类算法参数多且参数设定影响分类准确率的问题，采用Relief-F算法计算特征向量的分类权重，选择权重大者构成最终的特征向量，剔除了冗余特征。最后，再利用运算速度快、参数设置少的ELM进行故障诊断。试验结果证明，该方法能够有效运用于风电机组齿轮箱故障诊断中。