基于改进的多传感器自适应加权融合算法研究
周思益,张江梅,冯兴华,陈 浩
(西南科技大学信息工程学院,四川 绵阳 621010)
0 引言
近年来,随着传感器技术的不断发展,多传感器融合数据技术已成为研究热点。对多个传感器数据综合处理后的结果比单一传感器采集的数据更完整、更精确,对数据的处理和利用更合理[1]。
目前,融合算法主要有以贝叶斯估计[2]、D-S证据理论[3]和卡尔曼滤波[4]等为主的推理类和以神经网络[5]及专家系统等为主的人工智能类。但在众多的数据融合算法中,加权融合算法以不需任何先验知识、融合结果精度较高等优点而得到了广泛的研究。蒋君杰等[6]采用最大最小贴近度来定义贴近度矩阵,得到一种数据加权融合方法。万树平[7]从融合算法的稳健性角度,提出最小一乘估计进行加权融合权值分配。敬雪如等[8]基于支持度理论处理偏差较大的值,结合自适应加权算法进行数据融合。杨军佳等[9]通过对传感器实测数据的统计分析,进行各传感器加权融合的最优权值确定。刑晓辰等[10]将修正证据距离引入传感器实测数据间的距离计算,在实际测量精度基础上生成最终加权融合权值。王浩等[11]考虑到外界因素对采集数据精度的影响,在自适应加权融合算法的基础上,通过对系统待测真值的选取进行改进,以提高融合结果的精确度。
以上加权融合方法都得到较好的融合结果。但这些方法在融合时,存在未考虑偏差数据或对偏差数据直接剔除导致融合信息不准确,以及在融合时对某些参数的选取有在很强的主观因素等问题,导致融合稳健性不高;此外,还存在算法复杂、计算量大的不足,会影响融合实时性。
本文针对以上问题,首先提出在数据预处理阶段采用数据检验方法查找异常数据,并基于支持度理论构造了一种新的支持度函数,对异常数据进行替换。这可在减少融合信息丢失的同时得到最优的融合数据。其次,为提高融合稳健性和准确性,根据实测数据,提出基于优化传感器方差理论进行最优实测权值分配方法;同时,考虑传感器自身精度,利用传感器初始精度对各传感器进行固定权值的分配,综合实测权值和固定权值,得到最终的融合权值。
1 数据的异常值检验
在多传感器采集得到测量的原始数据中,有的数据是真实、有效的,有的数据由于随机影响因子的干扰,并不是有效数据。所以,要使融合的数据真实、有效,必须先对数据进行异常值检验。
在目前的数据探测技术中,常用的异常数据检测方法有:拉依达准则(也称3σ准则)、格罗布斯准则和分布图法。其中,拉依达准则在测量次数较大的情况下应用。在测量次数少于10次时,该准则是失效的。格罗布斯准则和分布图法都不受样本数据容量大小的制约。但是由于格罗布斯准则对单个或多个疏失误差的检测都有较好的效果,所以在实际测试分析中得到了大量应用。故本文采用格罗布斯准则对异常数据进行检验。
设n个传感器对某一待测指标的检测是彼此独立的,则利用格罗布斯准则检验异常数据的步骤如下。
①将每一组测量数据(服从正态分布)按x1≤x2≤...≤xn的上升顺序排列。
②测量数据xi求解算术平均值和标准差:
(1)
(2)
③根据格罗布斯准则统计,计算每个数据对应的gi值:
(3)
④以α作为显著性水平参数,一般取值为0.05、0.025、0.01等;查表寻找格罗布斯准则统计的临界值,即p[gi≥g0(n,α)]=α,其对应的测量数据则为异常数据。
利用上述方法逐一对每组测量数据进行异常值检测,查找原始数据中的异常数据。
2 基于传感器间支持度的异常数据替换
对于n个独立测量的传感器,设xi为测量值、εi为测量噪声、x为真值,则其中某一传感器测量方程可表示为:
xi=x+εi,i=1,2,...,n
(4)
对于传感器间支持度,本文在Jousselme证据距离[12]基础上,定义传感器i和传感器j之间的测量距离为:
(5)
对传感器的测量距离进行归一化处理,则归一化的距离为:
i,j=1,2,...,n
(6)
由式(6)可知:0≤dij≤1;dij越大,说明传感器间测量值的差距越大,则传感器之间的支持越小;相反,dij越小,说明传感器间测量数据的差距越小,即传感器间的支持越大。据此,可以定义1个支持度函数Sij。其应满足以下3个条件。
①当dij=0时,Sij=1。
②Sij是关于测量距离dij的单调递减函数。
③0 本文根据以上3个条件,提出1种新的支持度函数: (7) 进而构造出支持度矩阵S: (8) 根据支持度矩阵,定义i个传感器被其他传感器支持的支持度为: (9) 根据各传感器的支持度,将异常数据替换为支持度最高的传感器测量的数据,构成最优融合数据集。 目前,大多数的加权融合算法中都是采用传感器的测量方差来进行权值的分配的,并且大多采用传感器的自身精度或专家经验确定,并未考虑环境中随机因子的影响。这些方式确定的方差并不能有效地进行权值的分配。故本文在此处提出优化传感器测量方差的自适应加权方法。 (10) (11) 另有: (12) (13) (14) 根据式(13)和式(14),可计算出第i个传感器的测量方差,为: (15) 自适应加权数据融合是依据每个传感器实时测量的数据,通过计算每个传感器的测量方差,采用总均方差最小的原则,自适应地为每个传感器分配最优的权值,使得融合结果达到最优。自适应加权融合模型如图1所示。 图1 自适应加权融合模型Fig 1 Adaptive weighted fusion model (16) 式中:σ2为总均方差,是各加权因子wi的多元二次函数。 (17) 根据式(13)可知,要使总均方差σ2最小,f(w1,w2,...,wn)需取极小值。因此,根据多元函数的极值定理可得: (18) 通过将式(18)代入式(16),可求解w1,w2,...,wn的值;同时,定义w1,w2,...,wn为传感器的实测最优权值。 在n个传感器初始精度σ′1,σ′2,...,σ′n已知的情况下,将对根据初始精度进行各个传感器的固定权值w′1,w′2,...,w′n的分配。定义分配固定权值的计算公式为: (19) 根据实际情况,对实测最优权值和固定权值进行综合,取得最优的融合权值W。 (20) 式中:p为实测最优权值所占比重;q为固定权值所占比重。 将最终权值及融合数据代入式(16),即可得到融合结果。 表1 各传感器在各时刻的测量值表 各算法融合结果如表2所示。 表2 各算法融合结果 从表2可以看出,算术平均法只有在传感器自身的采集数据精度相当高的情况下,才会具有较好融合效果。若采集数据与实际值具有较大的偏差,融合的精度将会大大降低。传统自适应加权法虽然总体标准偏差δ和极限偏差Δmax的性能相对于算术平均法较好,但从单个时刻的融合结果来看,融合准确度不高。本文算法不仅融合指标δ和Δmax的性能良好,而且从单个时刻的融合结果来看,同样具有很好的融合准确度。各算法融合结果对比和融合结果绝对误差对比分别如图2和图3所示。 图2 各算法融合结果对比图Fig 2 Comparison of fusion results of each algorithm 图3 各算法融合结果绝对误差对比图Fig 3 Comparison graph of absolute errors of fusion resultsof each algorithm 本文研究了目前在数据融合方面比较关注的加权融合方法,针对目前在加权融合方法存在的问题,提出了一种综合考虑传感器初始精度和采集数据中的测量误差的自适应加权融合算法。为了充分、合理地利用各传感器采集的原始数据,该算法基于测量距离矩阵提出一种新的支持度函数,确保在剔除偏差较大的误差值的同时减少融合信息的丢失。此外,在测量时考虑环境影响,提出一种优化的实测最优权值分配方法,根据传感器自身精度计算传感器的固定权值,根据实际情况,以综合固定权值和实测最优权值作为算法的最终融合权值。最后,通过实际算例与其他算法进行对比,验证了该融合算法的有效性。3 基于优化传感器测量方差的自适应加权
3.1 优化传感器测量方差


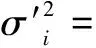


3.2 自适应加权数据融合


3.3 固定权值分配
4 算法实例与结果分析






5 结论

