基于ARJI-GARCH模型的中国上市银行跳跃风险传染网络研究

王周伟 张 政

一、引 言

金融业的稳定发展需要对系统性金融风险加以预先防范。系统性金融风险形成的关键在于复杂关联传染，防控的关键也就在于抑制关联传染。已有研究表明，银行风险传染的路径主要有股市信息关联传染、同业拆借业务关联传染等。其中股市信息关联传染涉及金融事件信息冲击、资产定价、市场均衡状态及信息传递等环节，其机理最为复杂，一直是国内外学界研究的焦点。

技术方面，系统性金融风险的度量模型被不断推进。谷耀和陆丽娜①谷耀、陆丽娜：《沪、深、港股市信息溢出效应与动态相关性——基于DCC-（BV）EGARCH-VAR的检验》，《数量经济技术经济研究》2006年第8期，第142—151页。较早把收益与波动作为股市信息波动的代理变量，用DCC-(BV)EGARCH-VAR模型测度了沪、深、港三个股市间的信息溢出效应；刘向丽等①刘向丽、成思危、汪寿阳等：《期现货市场间信息溢出效应研究》，《管理科学学报》2008年第3期，第125—139页。用AR-GARCH模型估算了标准正态分布下的波动和风险价值，用格兰杰因果关系检验法，分别验证了期现货两个市场的均值、波动和风险之间的信息溢出效应；等等。上述文献先后拓展了研究对象，但属于分别验证，割裂了均值、波动和风险等一阶矩与二阶矩之间的关联；李红权等②李红权、洪永淼、汪寿阳：《我国A股市场与美股、港股的互动关系研究：基于信息溢出视角》《经济研究》2011年第8期，第15—25+37页。提出了基于交叉相关系数的信息溢出全方位检验体系，同时揭示了股市均值、波动和风险的信息传递全景图，包括互动的方式、方向、相对强度、当期影响与多期滞后关系以及时变性，该文献的分析视域为两两分析，缺乏全系统观；梁琪等③梁琪、李政、郝项超：《中国股票市场国际化研究：基于信息溢出的视角》，《经济研究》2015年第4期，第150—164页。以收益率为风险代理信息，利用有向无环图和溢出指数法，把两两信息溢出拓展为多维信息溢出；李政等④李政、梁琪、涂晓枫：《我国上市金融机构关联性研究——基于网络分析法》，《金融研究》2016年第8期，第95—110页。用VECM模型的格兰杰因果关系检验构建了信息溢出关联的有向含权网络，拓展出信息溢出网络分析；徐晓光等⑤徐晓光、廖文欣、郑尊信：《沪港通背景下行业间波动溢出效应及形成机理》，《数量经济技术经济研究》2017年第3期，第112—127页。利用广义溢出指数法分析了行业间波动溢出效应；黄玮强等⑥黄玮强、庄新田、姚爽：《基于信息溢出网络的金融机构风险传染研究》，《系统管理学报》2018年第1期，第235—243页。做出网络拓扑结构特征分析；佟孟华等⑦佟孟华、邢秉昆、于洪涛：《中国银行间风险核心传递中介与系统性风险》，《金融论坛》2019年第7期，第20—31页。利用VAR模型和VECM模型及格兰杰因果关系检验法，构建有向无权的信息溢出网络。

上述文献在股市信息传染研究方面的探索卓有成效，但同时需要引起关注的是：第一，已有文献的信息变量主要集中在收益率及其均值与波动，而大量实证研究发现，其分布具有显著的右偏、尖峰、厚尾和集聚性特征，隐示极端风险发生概率极大，当前研究只关注了一、二阶矩风险信息关联传染，风险价值多据正态分布估算，忽视了跳跃成分及其决定的偏度和峰度的时变性，故而风险传染的强度、广度和深度估算结果比较粗糙，不能揭示极端风险溢出关联传染。第二，2015年中国股灾、2016年1月初中国股市两次触及两档熔断、2020年3月9日至20日美国股市十天内四次熔断、2020年4月21日美国 5月轻质原油期货价格暴跌约300%等等事实和文献研究均已表明，收益率变化普遍具有显著的连续扩散成分和离散跳跃成分，跳跃不仅显著正向影响波动，并且正向影响偏度和峰度。已有文献多数是利用传统GARCH模型预测波动，但该类模型主要考虑了连续波动部分，没有考虑由极端冲击和意外信息引发的高频跳跃信息，忽略极端金融事件冲击形成的风险扩（散）增（幅）加速机制。

鉴于此，本文创新性地采用了自回归跳跃强度的跳跃GARCH模型，即ARJIGARCH模型。统一测度跳跃和预测条件波动，调整计算时变的偏度和峰度，与ARJIGARCH模型逻辑一致地依据一般分布计算修正风险价值，以综合反映银行股票收益率的一阶、二阶、三阶和四阶矩风险信息。随后基于VAR模型的广义方差分解技术，测度信息关联度，构建系统信息关联度网络矩阵，进行风险信息传染分析及复杂网络分析。

本研究的主要贡献在于：第一，中国股市普遍具有显著跳跃性，跳跃正向影响股价波动，跳跃具有集聚性和杠杆效应①赵华：《中国股市的跳跃性与杠杆效应——基于已实现极差方差的研究》，《金融研究》2012年第11期，第179—192页。，具有时变性、集聚性和跨期依赖等特征，于是选用ARJI-GARCH模型，预测条件波动率；股票收益率跳跃强化了尖峰、厚尾和右偏的高阶矩非高斯特征，不同于一些文献依然使用正态分布分位数定义估算风险价值，本文调整了正态分布的偏度和峰度，再利用一般分布意义的风险价值估算式，因此本文不仅在统一框架中预测了跳跃波动和条件波动率，而且逻辑一致地计算了跳跃风险价值。第二，用修正跳跃风险价值，综合测度极端事件和意外冲击下的银行风险，用基于VAR模型的广义方差分析技术，测度风险溢出和风险吸收指数，构建系统性风险溢出矩阵，分析银行极端风险关联传染效应，从而拓展了银行风险传染研究。

二、研究设计

（一） ARJI-GARCH模型及其估计

极端事件冲击时，股价会普遍发生显著异质性跳跃，跳跃具有时变性、集聚性和跨期依赖等特征。与其他跳跃GARCH模型相比，ARJI-GARCH模型可以在较好拟合时序金融数据的同时，最为有效地拟合具有特征的股价跳跃。因此本文选用ARJI-GARCH模型识别估算连续波动和跳跃波动。

1.ARJI-GARCH模型设定

ARJI-GARCH(1,1)模型是在普通GARCH(1,1)模型的均值方程中增加跳跃项。根据样本收益率特征，可设定均值方程为AR（2）：

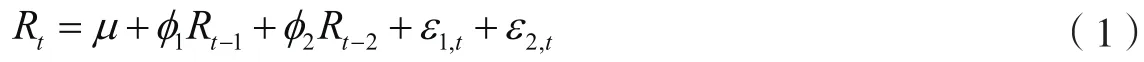
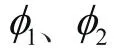
其连续波动为：

跳跃波动为：

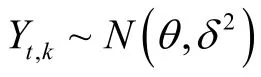
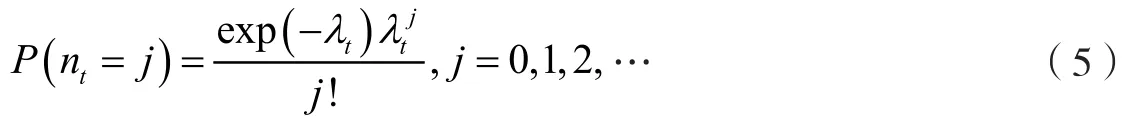
跳跃强度是时变的，具有集聚性，ARJI-GARCH模型设跳跃强度λt服从ARMA(1,1)过程：

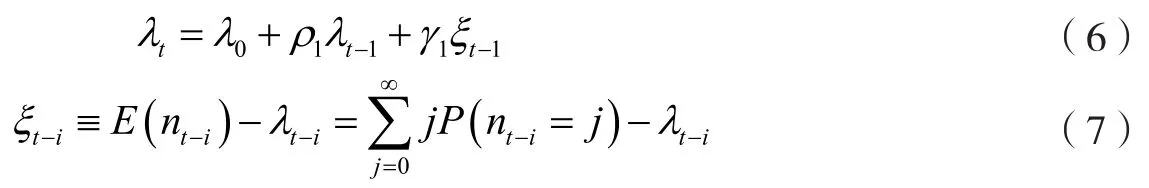
2.ARJI-GARCH模型的参数估计方法

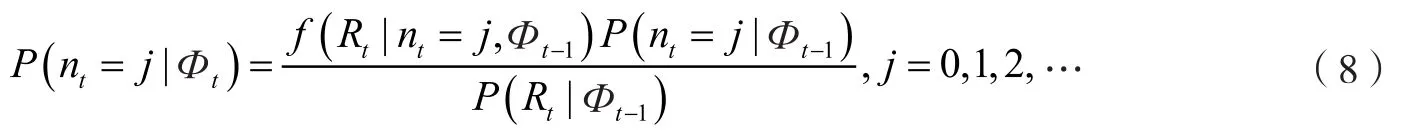
由全概率公式可得：

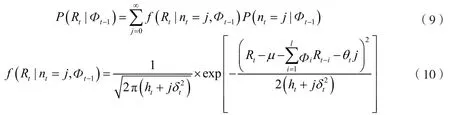
则对数似然函数为：

3.ARJI-GARCH模型的条件波动率预测及其有效性评价

ARJI-GARCH模型的条件波动率预测式为：

为比较评价GARCH模型、JUMP-GARCH模型和ARJI-GARCH模型的预测效果，利用2008—2018年的数据估计模型，然后利用所估计的模型对余下的数据点进行预测，计算预测误差指标，评价模型预测功能。假设预测样本期为t=T+1,…,T+h，计算预测误差指标：

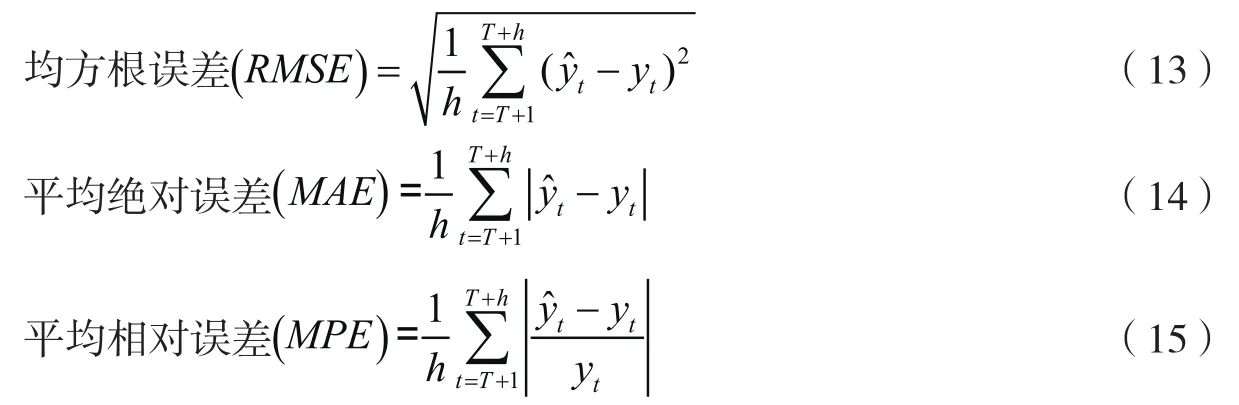
上述预测误差指标值越小，模型预测效果越好。

（二） 参数调整与风险价值的估算及其有效性评价

1.分布偏度、峰度与风险价值的调整计算

已实现二阶矩来源于连续波动和跳跃波动两个部分，已实现偏度和已实现峰度只决定于跳跃部分。①王宜峰、范时昊、张晓磊：《已实现高阶矩的风险传染效应：基于马尔科夫机制转换的实证分析》，《系统管理学报》2019年第4期，第652—659页。而跳跃GARCH模型都假设收益率跳跃幅度及其总跳跃幅度服从一般正态分布，但其实际分布并不是跳跃GARCH模型假设的正态分布，具有尖峰、厚尾与杠杆效应等非高斯特征，正态分布假设不能刻画跳跃波动中的此类程式化现象②宫晓莉、熊熊、庄新田：《广义双指数分布的跳跃扩散模型下股指期货波动研究》，《管理科学》2018年第3期，第149—159页。，因此应用条件波动率预测值计算风险价值时，需要调整偏度系数 和峰度系数，调整计算式③Das S R,Sundaram R K.“Taming the Skew:Higher-Order Moments in Modeling Asset Price Processes in Finance”,Working paper,1997.为：

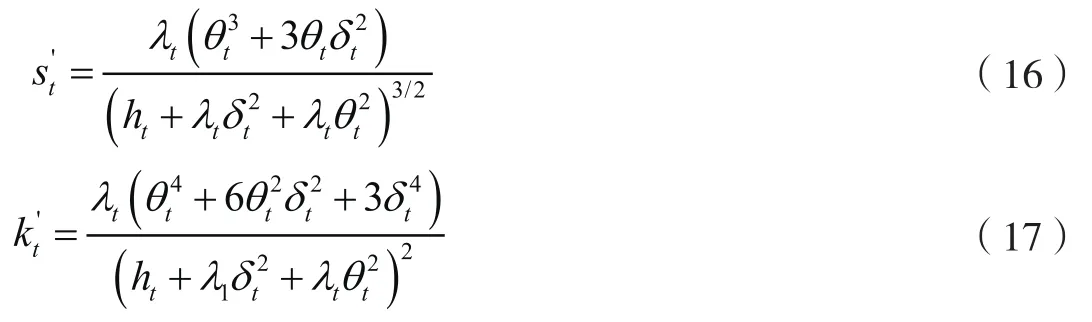
然后，把调整后的偏度系数和峰度系数代入一般分布意义下的VaR计算式④许启发、张金秀、蒋翠侠：《基于支持向量分位数回归多期VaR测度》，《系统工程学报》2014年第2期，第202—214页。，可得修正的VaR计算公式：

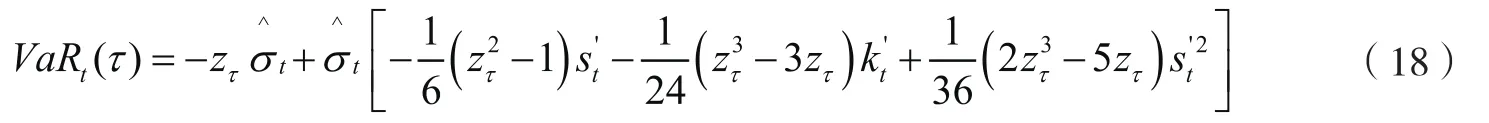
其中，为置信水平 对应的标准正态分布分位数。

2.风险价值计算结果的有效性评价

依据GARCH模型、JUMP-GARCH模型和ARJI-GARCH模型的条件波动率预测值，计算出风险价值的结果，它们的有效性会有差异，采用Kupiec失败频率检验进行有效性评价。原假设:实际失败率与设定的α相等，即N/T=α。

检验统计量为：

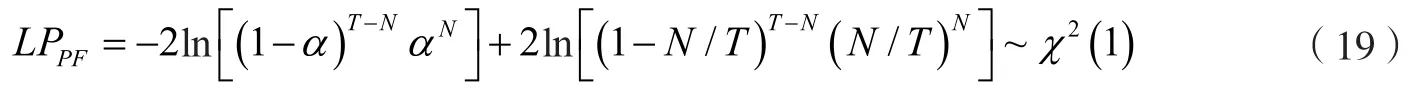
其中，N为实际收益率小于VaR的天数，即失败天数；T为总的考察天数。

（三）银行风险关联传染网络的构建与分析方法

1.跳跃风险关联传染网络的构建方法

股价信息关联的常用测度方法主要有相关系数法、连接函数Copula法、格兰杰因果关联检验法和向量自回归模型。相关系数法和连接函数Copula法能够测度相关关联程度及其显著性，但无法测度关联方向，无法构建有向含权网络；格兰杰因果关联检验法能够检验关联的显著性和方向，但无法测度出关联程度，只能用于构建有向无权网络。而向量自回归模型属于多方程交互模型，可以利用其广义方差分解技术，系统估算出任意两只股价收益率之间的不对称双向关联程度和显著性，由此可构建出有向含权关联网络及矩阵，便于做进一步的深化分析。因此本文对上市银行跳跃风险价值构建向量自回归（VAR）模型，测度风险关联传染程度，构建有向含权的跳跃风险关联传染网络。

具有平稳协方差的滞后期h的N个样本变量VAR（h）模型为：

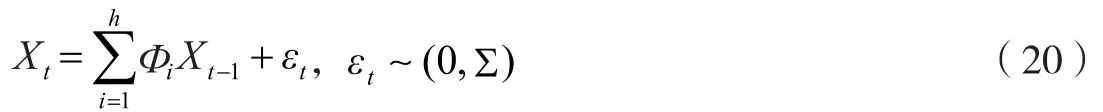
借助广义方差分解技术，计算向前H步的机构之间的有向关联系数：

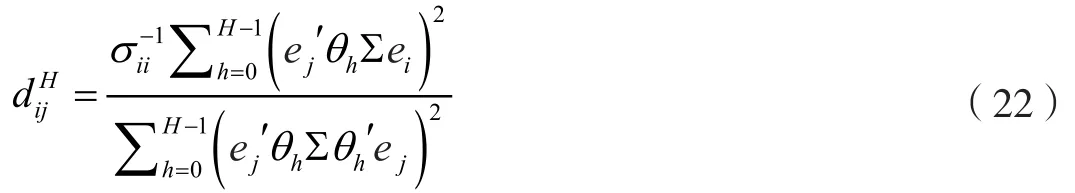
建立有向含权关联度矩阵，如表1所示：

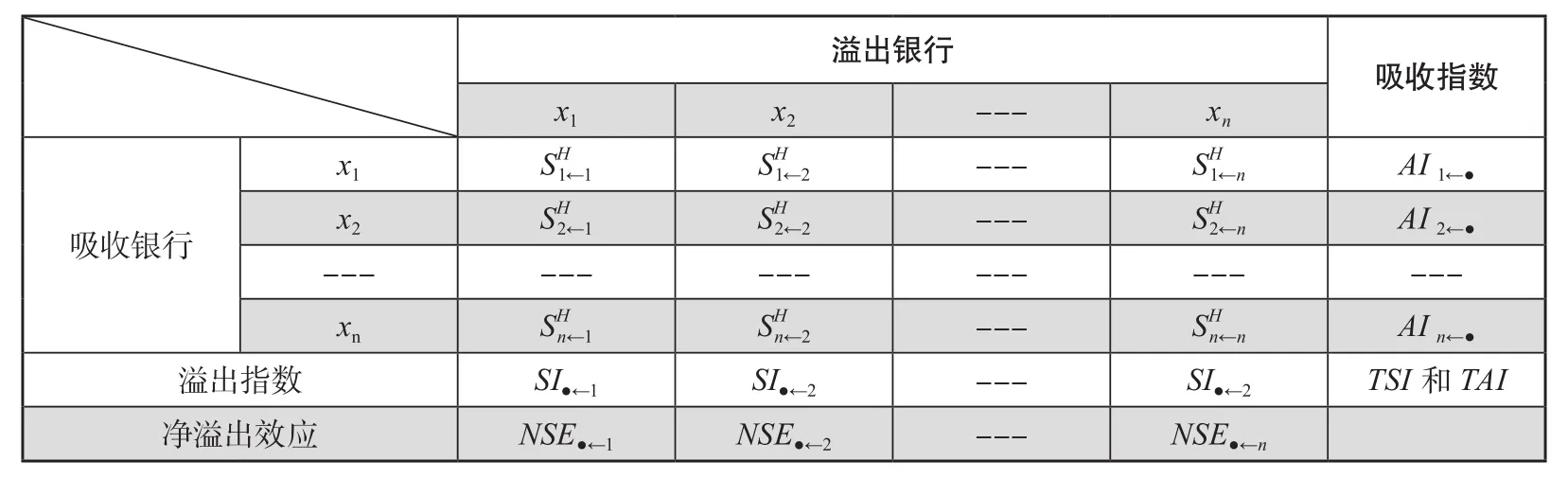
表1 有向含权的系统性风险溢出关联度矩阵

2.跳跃风险关联的网络分析与风险分析方法

（1）风险溢出传染分析指标

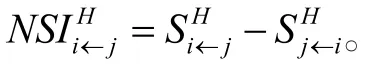
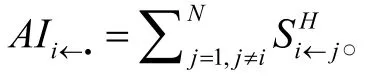
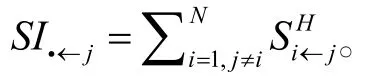
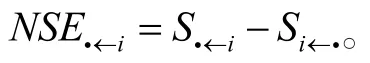
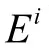
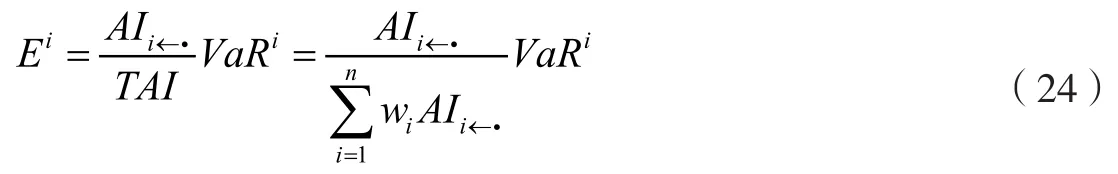
定义银行j系统性金融风险贡献指数Cj为：

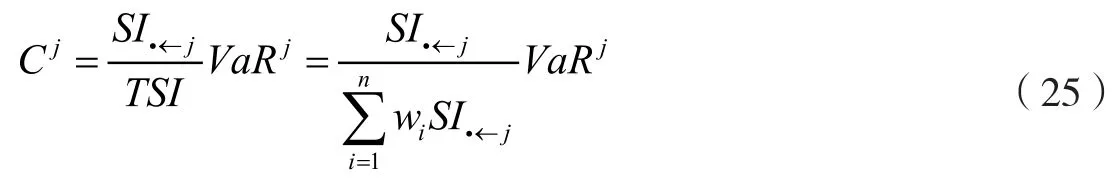
该指数表示当银行j发生风险损失时，该风险将成比例地向系统中的其他银行溢出。

（2）网络总体特征分析指标

网络关联度反映了跳跃风险关联网络自身的稳健性和脆弱性。网络关联度越高，说明某些银行与较多的银行关联，这些银行的稳健关乎网络安全，网络脆弱性就高。计算式为：

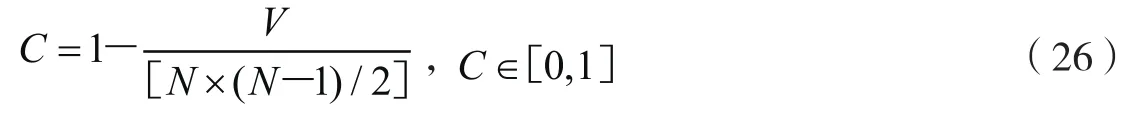
其中：C为网络关联度；N为银行数量；V为网络中不可达的点对数。

网络等级度H反映的是网络中银行之间非对称的可达程度，以及网络中各银行的等级结构。网络等级度越高则跳跃风险关联网络中银行之间的等级层级越多，越多的银行在跳跃风险关联网络中将处于从属和边缘地位。计算式为：

其中，K为表征网络中对称可达的点对数，最大可能对称可达的点对数用max(K)来表示。

网络密度是网络中实际存在的边数与可容纳的边数上限的比值。它反映跳跃风险关联网络的紧密程度。网络密度越大，则银行之间风险溢出关联就越紧密，跳跃风险关联的网络结构对各银行风险产生的传染影响也越大。一个具有N个节点和L条连接边的网络，其网络密度为：

网络密度取值范围为[0,1]。当网络为全连通时，d(G)=1；当网络中不存在连边关系时，d(G)=0。

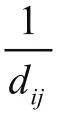
网络效率反映了银行间跳跃风险空间关联网络中各银行之间的连接效率。计算式为：

若网络效率越低，平均路径长度越大，则说明银行间关联距离越大，银行关联路径中存在较多的连线，两个机构之间的风险传染需要经过较多的节点，银行间跳跃风险关联网络就越稳定。

（3）银行的网络中心性和网络优势特征分析指标

有向含权网络中，各节点的网络中心性测度指标主要有出（入）度数中心度、出（入）接近中心度、中介中心度和出（入）特征向量中心度等，网络优势地位用限制度反映，如表2所示。

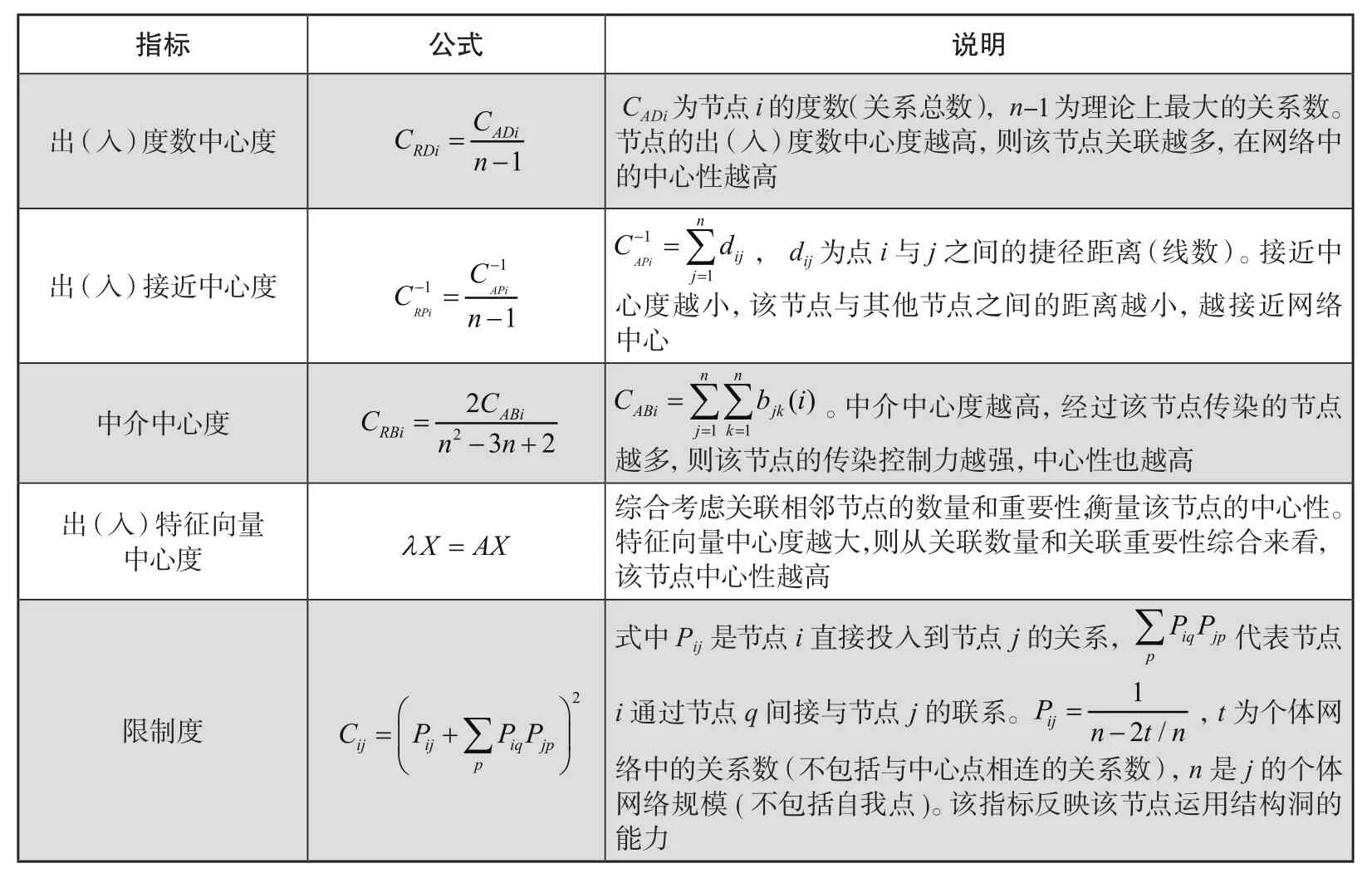
表2 网络中心性测度指标

（4）银行角色群体的块模型分析

块模型是一种网络节点角色归类的方法。该方法先用CONCOR法及层次聚类方法对网络节点进行分类，再比较该节点实际内外关联数量占比与所在群体的期望内外关联占比大小组合，把网络节点归类为净受溢者、双向溢出者、经纪人和净溢出者四种角色①王周伟、刘少伟、魏伟等：《中国地方政府债务风险关联网络的空间特征与影响因素》，《统计与信息论坛》2019年第12期，第22—31页。。设群体Bk中有gk个行动者，在网络节点总体中有g个行动者，归类规则如表3所示，由此可得到风险传染网络角色划分结果。

表3 风险溢出关联角色分类

三、实证结果与分析

（一）样本选择及数据来源

样本选取2008年之前上市的14家商业银行，收集2008年1月1日至2019年12月31日期间这些银行股票的收盘价，剔除非交易日期，共2 925条数据，数据均来自Wind数据库。选取收盘价对数一阶差分来计算每日的对数收益，得到各家银行的对数收益率，并将其扩大100倍。

（二）样本数据的描述性分析

表4给出了14家商业银行对数收益率的基本统计特征。

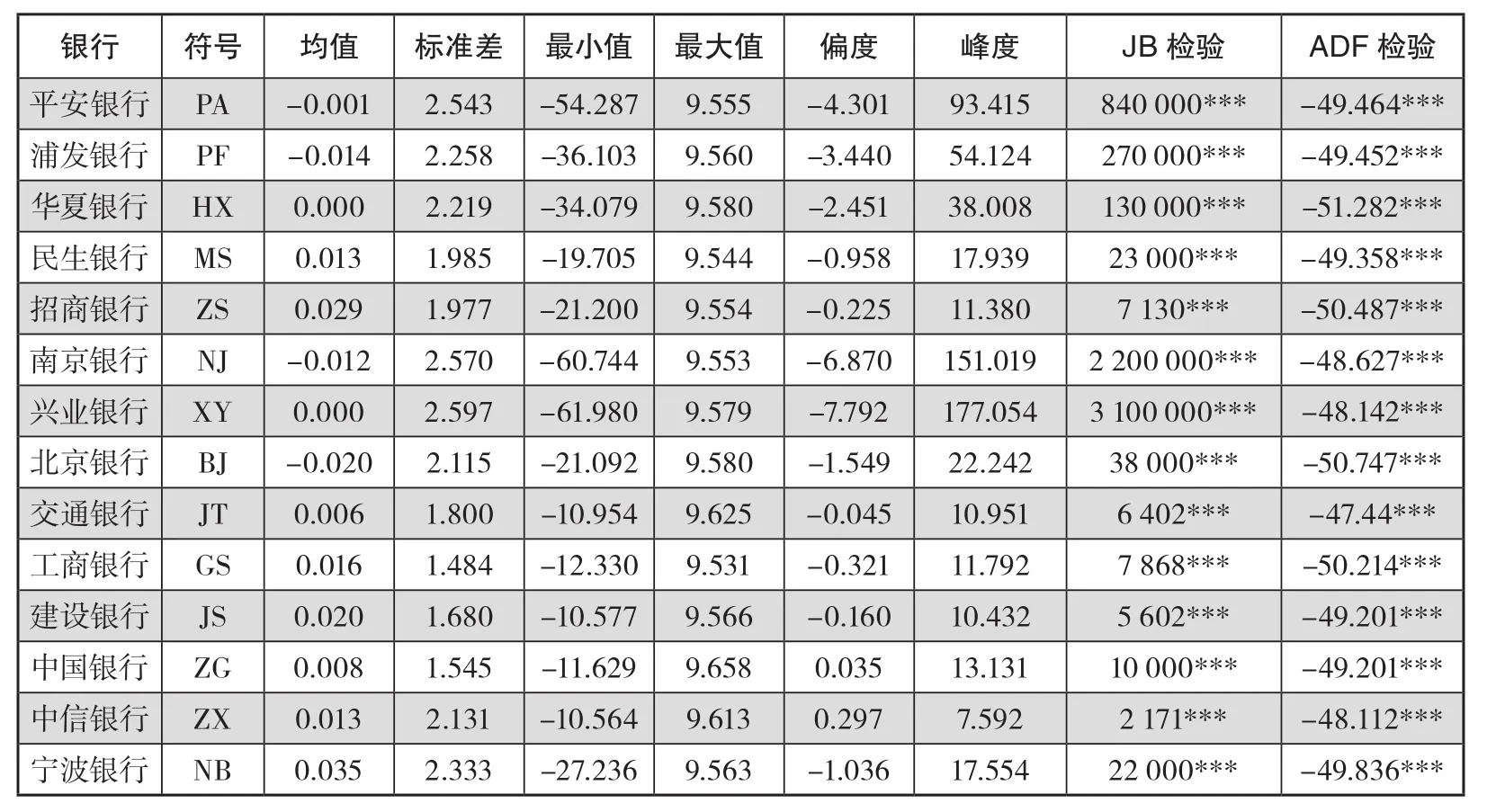
表4 变量描述性统计

由表4可知，各家银行的收益率均值位于0附近，反映了收益率以0为中心上下波动的特征，收益率的标准差均较大，说明其跳跃波动较为频繁显著。另外，样本中的各上市银行收益率的偏度都不为0，峰度也都大于3，J-B统计量均不接近0，说明所选取的14家上市银行收益率都呈现出了典型的尖峰、厚尾特征。此外，从各上市银行收益率的ADF检验来看，ADF的P值均接近0，即所选取的样本中的收益率时间序列均是平稳的，从而保证了模型建立的稳健性。

（三）ARJI-GARCH模型的参数估计结果与有效性评价

14家上市银行日对数收益率的自相关系数拖尾，偏自相关二阶截尾，于是收益率连续均值方程选用AR（2）模型；ARCH LM检验显示收益率残差具有ARCH效应，需用GARCH模型，而残差平方相关图表明存在一阶ARCH效应，建立GARCH（1,1）模型拟合。以一倍正负标准差为门限值观察识别条件残差跳跃，发现样本期间，受2008年全球金融危机、2013年钱荒、2015年股灾和2016年熔断等极端金融事件和意外冲击影响，收益率都有显著的多次大幅跳跃，这些跳跃具有集聚性与不对称性特征。因此经过多次试算，选用AIC和SC值最小的ARMA（1,1）模型拟合跳跃强度变化，用ARJI-GARCH（1,1）模型拟合14家上市银行的日对数收益率序列，估计模型参数，预测条件波动率。结果如表5所示。

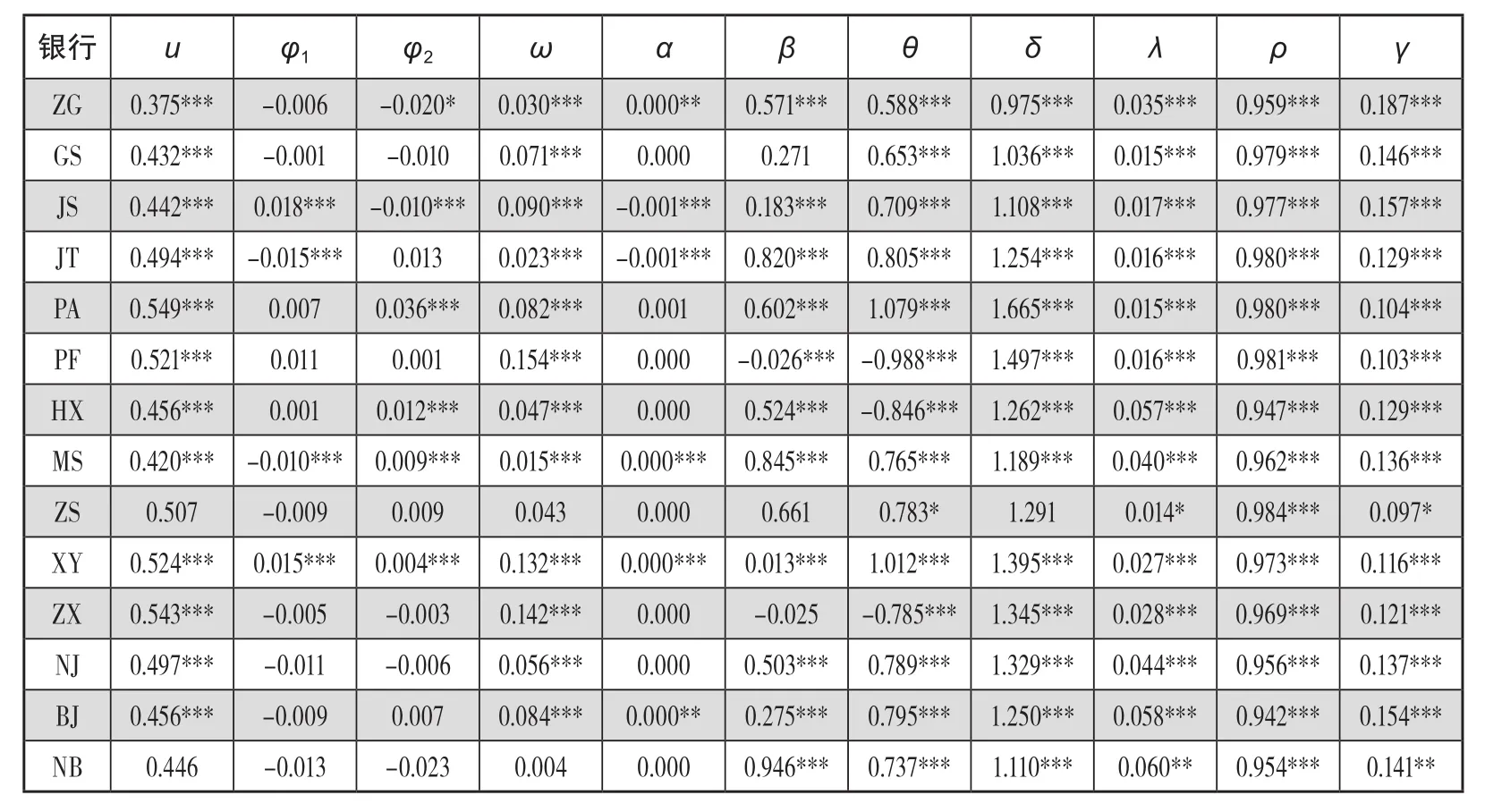
表5 样本银行的ARJI-GARCH模型参数估计

由表5可知，所有样本银行收益率的跳跃幅度的均值和方差参数都是在1%显著水平上显著，而跳跃次数的跳跃强度，招商银行收益率在10%显著水平上显著，宁波银行收益率在5%显著水平上显著，其他所有银行收益率跳跃次数的跳跃强度都在1%显著水平上显著，所有银行收益率的一阶自相关跳跃强度系数和一阶移动平均项系数都在1%显著水平上显著，说明这些显著跳跃都具有集聚性。说明选用ARJI-GARCH（1,1）拟合是比较合适的。

利用式（13）、（14）和（15），汇总计算样本银行条件波动率预测偏差，结果见表6。

表6 模型预测效果比较

由表6可知，ARJI-GARCH（1,1）模型的三个预测偏差指标值都是最小，说明其预测效果更好。宏观审慎监管需要较准确高效的风险监测，于是选用ARJI-GARCH模型预测包含连续波动和跳跃波动的条件波动率。

（四）基于ARJI-GARCH模型的VaR估算结果与有效性评价

利用式（12）预测银行条件波动率，根据公式（16）、（17）计算得到修正的偏度系数St和峰度系数kt，代入修正后的VaR测度公式（18），取τ=0.05，计算得到样本银行风险价值。其描述统计结果如表7所示。

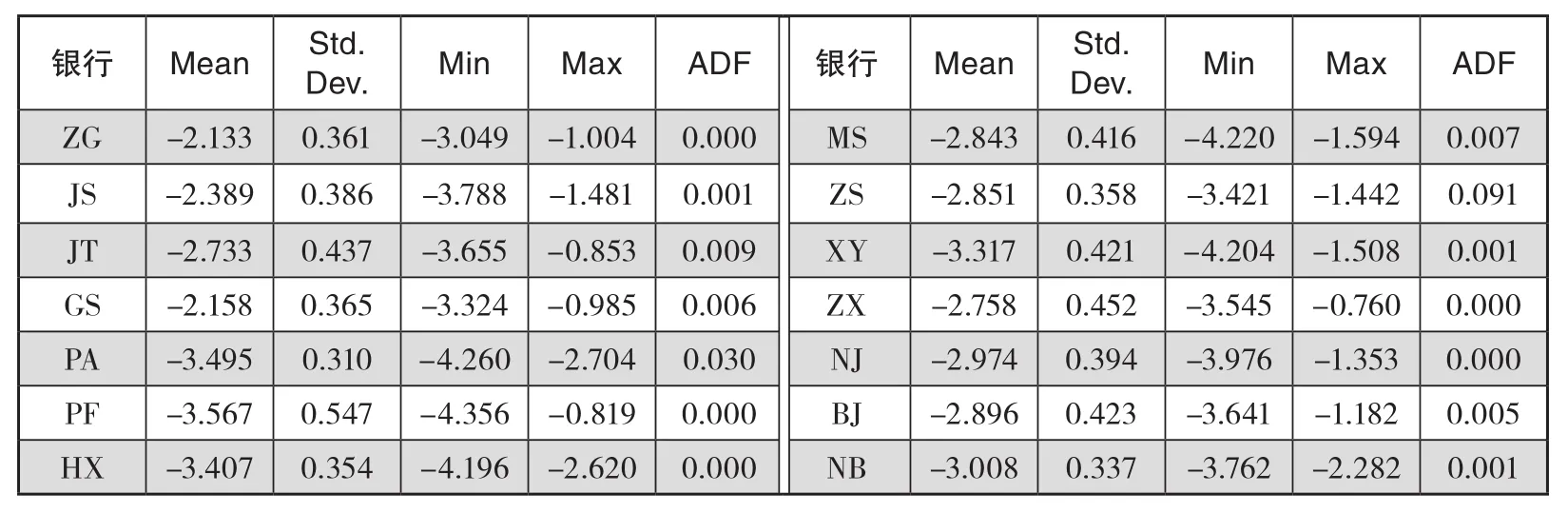
表7 银行风险价值的描述性统计

银行风险价值VaR的绝对值越大，表示面对风险冲击时该银行自身的风险越高，从表7可以看出，国有制银行的风险价值VaR绝对值及其标准差普遍最小，较其他银行更为稳健安全些。而股份制银行表现不一，中信银行和民生银行风险较小，但中信银行风险价值波动较大；平安银行风险为第二大，但风险变化不大，而浦发银行风险最大，且其风险波动也是最大。

Kupiec失败比率检验结果表明，利用ARJI-GARCH模型预测的条件波动率和修正的偏度和峰度计算的修正风险价值的失败比率最接近理论失败次数，在1%的显著水平下是显著的。

（五）银行间风险传染的网络构建结果与分析

1.银行风险传染的权重矩阵构建结果与分析

由表7中样本银行风险价值序列的ADF单位根检验结果可知，14个银行的风险价值序列均是平稳的，从而保证了模型建立的稳健性。按照模型AIC和SC值最小化准则，确定滞后阶数H=4，估计参数构建VAR（4）模型。再根据式（22）做广义方差分解分析得到关联度，得到银行跳跃风险传染的权重矩阵，计算每家银行的风险吸收效应、风险溢出效应、系统风险暴露、系统风险贡献及风险净溢出效应，及全部样本银行的总风险溢出。结果如表8所示。

由表8可知，第一，跳跃风险溢出效应结果表明，全样本银行间总风险溢出指数高达30.2%，这表明中国上市银行之间的风险溢出传染效应显著。就银行跳跃风险溢出效应和溢出效应而言，银行跳跃风险溢出效应差异不大，招商银行跳跃风险溢出效应第二大，跳跃风险吸收效应最小，其风险净溢出效应最大，系统重要性最强；交通银行跳跃风险溢出效应最大，跳跃风险吸收效应较小，其风险净溢出效应第二，系统重要性很强。第二，跳跃风险吸收效应结果表明，银行跳跃风险吸收效应差异较大，极差为46.5；建设银行、中国银行和工商银行三家国有银行风险吸收效应较大，建设银行的跳跃风险吸收效应最大，中国银行、华夏银行和南京银行的跳跃风险吸收效应为第二梯队，这些银行最容易遭受关联银行跳跃风险传染冲击，较为脆弱。第三，从反映风险传染扩散能力的系统风险贡献来看，平安银行和浦发银行的系统风险贡献最大，其次是交通银行、华夏银行、招商银行、兴业银行和北京银行。从反映跳跃风险吸收的系统风险暴露来看，建设银行、华夏银行和南京银行的系统风险暴露较高，位于前三。

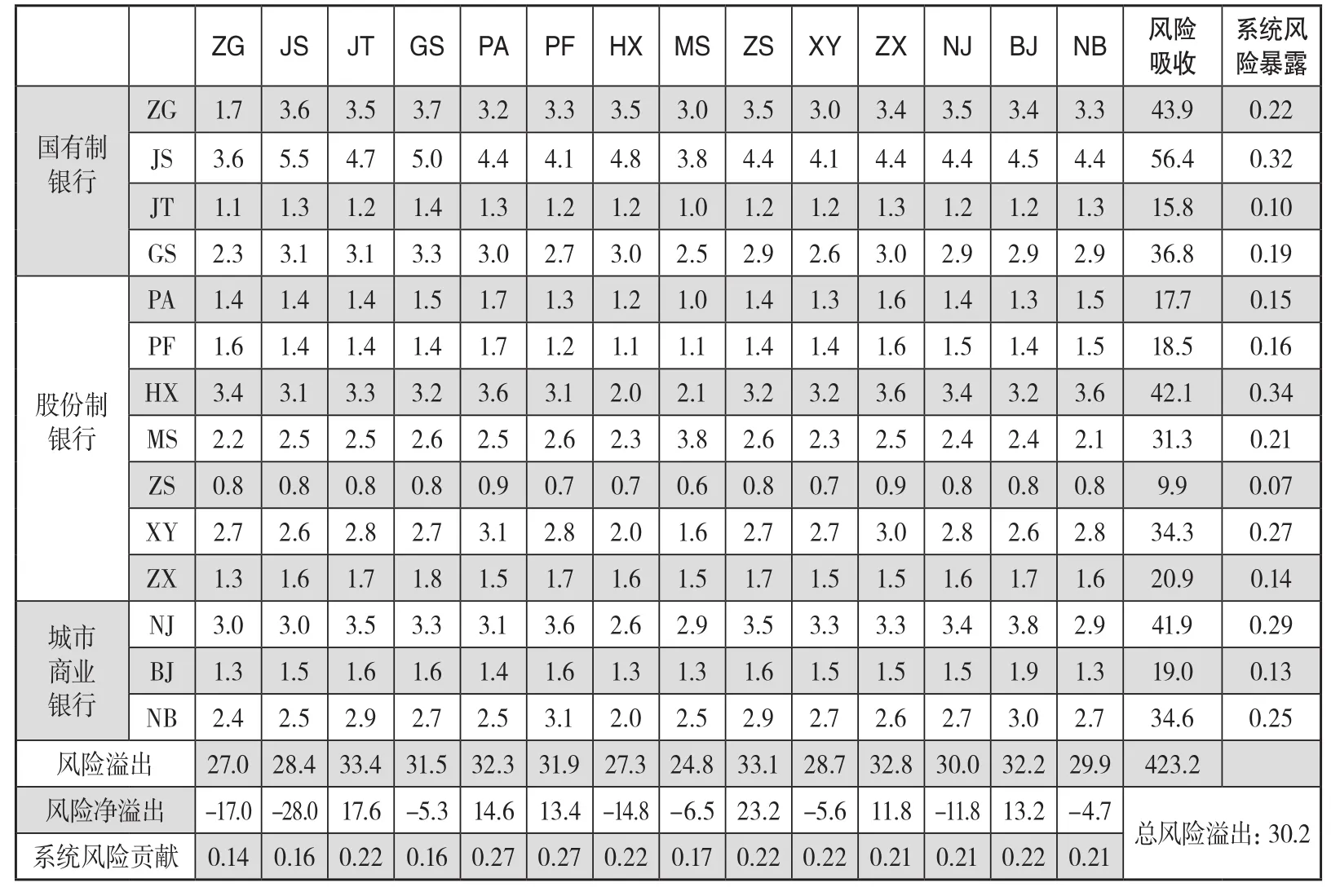
表8 银行跳跃风险传染的权重矩阵 单位：%

三种所有制银行的五个风险传染指标的平均值，如表9所示。

表9 分所有制的平均风险指数

由表9可知，三类银行的平均风险溢出效应相近，而风险吸收效应差异较大，国有制银行最大，城市商业银行次之，股份制银行最小；与二者对应，股份制银行的风险净溢出效应最大，国有制银行和城市商业银行主要是吸收效应。从风险贡献指数来看，股份制银行、城市商业银行显著大于国有制银行；从系统风险暴露指数来看，各银行类型的系统风险暴露指数差异不是很大。这说明我国国有制银行资产规模较大，但业务经营合规保守，信息披露充分，外部冲击免疫力较强，不会对其他关联银行发生关联传染，分散吸收系统性风险较多；相反，股份制银行经营相对激进，金融业务创新比重较大、复杂性强，风险承担较多，内外信息不对称程度较高，风险冲击缓释能力较弱，容易依信息关联路径传染风险，风险吸收能力也较弱。这一结论与胡利琴等人的结论①胡利琴、胡蝶、彭红枫：《机构关联、网络结构与银行业系统性风险传染——基于VAR-NETWORK模型的实证分析》，《国际金融研究》2018年第6期，第53—64页。基本一致。

2.邻接矩阵构建与银行风险传染网络图绘制结果及分析

选取银行风险传染的权重矩阵中除对角线外关联系数的平均数作为阈值水平（η=2.159），银行间关联度大于阈值，则元素取值为1，否则取值为0，将上市银行风险传染的权重矩阵X=(SHi←j)n×n转化为二值邻接矩阵Y=(Yij)n×n。

把权重矩阵和邻接矩阵对应元素相乘，得到有向含权网络矩阵，绘制银行间风险关联传导的有向含权网络图，见图1。可以看出，我国上市银行风险传染呈现出明显的空间网络特征，无孤立孤岛节点。

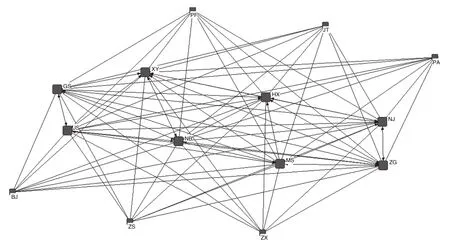
图1 上市银行间风险传导的空间关联网络图

3.上市银行间风险传染网络的总体特征与风险分析

从网络总体关联描述计算结果看，网络关联数为99，该网络的节点数为14个，平均关联数7.07，即平均每家上市银行与7家银行之间有显著的风险传染关系；整体网络关联度为1，即每家银行都可以直接或者间接通过相关银行与其他银行有风险传染关系，说明我国金融风险在上市银行间的传导具有明显的空间关联和溢出效应；网络等级为0.631 6，说明我国上市银行金融风险间的传导存在明显的等级结构。网络效率(为0.192 3)较低，则说明银行之间存在更多的连线，银行之间风险的联系更加紧密，也越容易通过银行间跳跃风险空间关联网络传染风险。网络密度（即聚类系数为0.544）较大，银行之间跳跃风险溢出比较紧密，单一银行爆发的极端跳跃风险极易通过整体网络溢向其他银行。网络平均路径长度为1.048，说明每家银行通过1到2家相关银行就会与其他银行关联传染风险，整体网络连接较为紧密，说明银行跳跃风险关联网络具有“小世界网络”特征①小世界网络模型是一类具有较小的平均路径长度又具有较高的聚类系数的网络的总称。，该网络中银行跳跃风险传染速度很快，风险扩（散）增（幅）加速机制作用较强，网络稳健性较弱。

4.风险传染网络中银行的中心性与地位优势分析

依据表2计算跳跃风险传染网络中的银行中心性指标，如表10所示。

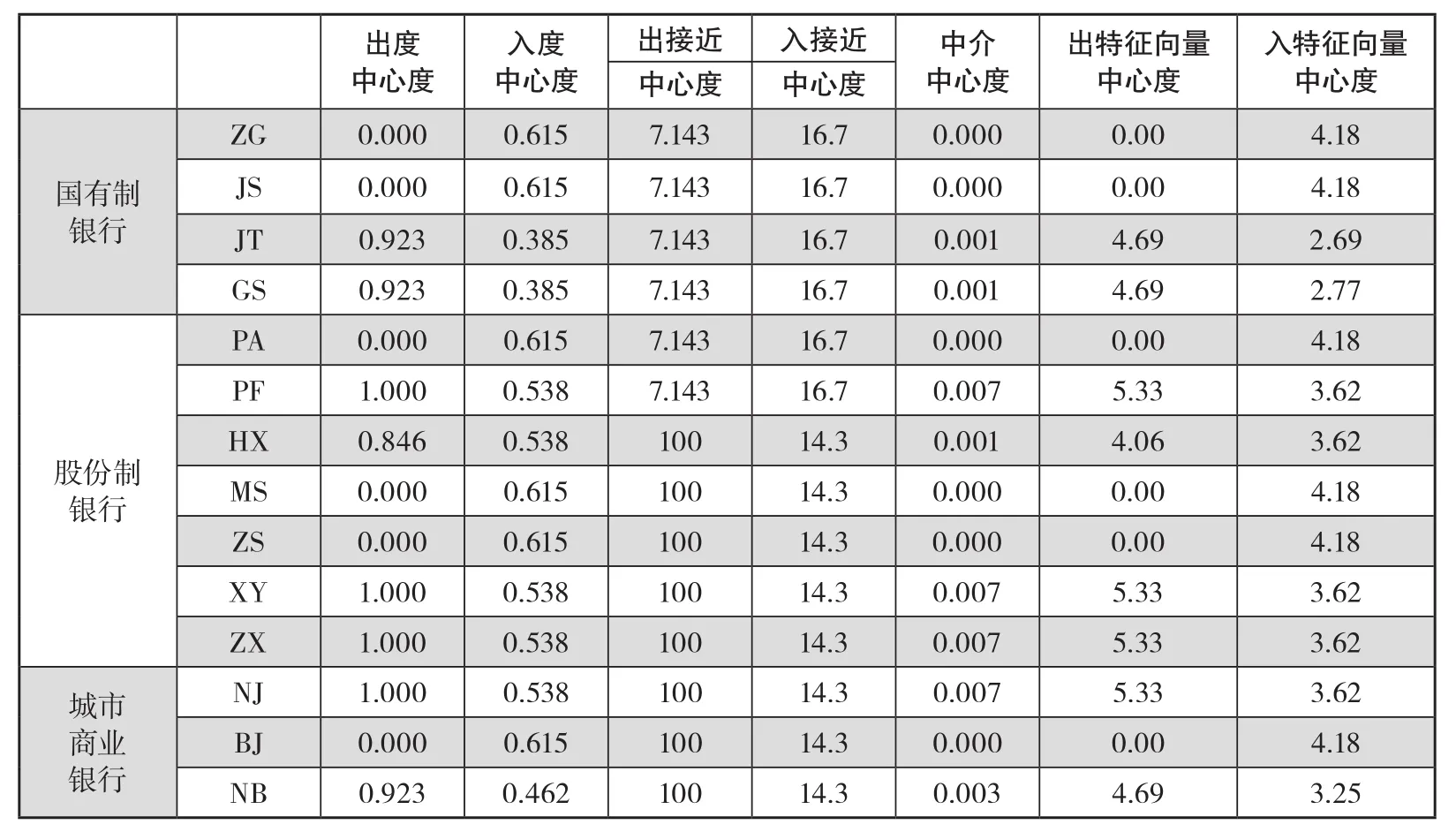
表10 银行重大风险网络中心度指标

由表10可知，浦发银行、兴业银行、中信银行和南京银行的出度中心度最大，说明这些银行的溢出传染效应范围最广。各银行的入度中心度差异不大，说明这些银行接受风险传染的范围基本相当。城市商业银行、股份制银行的出接近中心度较大，说明这些银行最接近溢出网络中心及各节点，最容易发出网络最广泛的最强传染。国有制银行、部分股份制银行的入接近中心度较大，说明这些银行最接近受传染网络中心，最容易受到网络最强传染。浦发银行、兴业银行、中信银行和南京银行的中介中心度最大，说明这些银行是网络中最强的传染中介。从特征向量中心度看，没有呈现出明显的银行类型差异，浦发银行、兴业银行、中信银行和南京银行的出特征向量中心度最大，最容易发出网络最广泛的最强传染；交通银行、工商银行和宁波银行为第二梯队，中国银行、建设银行、平安银行、民生银行、招商银行和北京银行的出特征向量中心度为0，说明这些银行的综合溢出传染关联数为0，反过来，这些银行的入特征向量中心度较高，说明其综合吸收传染效应较大。该网络中银行的出度中心度、出接近中心度和出特征向量中心度指标之间差异较大，节点度数分布呈现严重不均匀分布，基本符合幂律分布和zipf定律，说明该网络溢出关联具有“无标度”特征，容错性和稳健性较强，但如遇到针对风险净溢出效应较强和系统风险贡献较大的银行的选择性攻击，网络脆弱性很大。

总体网络结构洞可以很好地比较银行间的网络优势地位，结构洞计算结果显示，华夏银行和宁波银行的等级度最高，其运用风险网络结构洞的能力最强，而大多数银行的等级度都较高，表明这些银行的网络传染中介作用都较强。

5.风险传染网络中的银行角色块模型分析结果

利用CONCOR算法，设最大分割深度为2，收敛标准为0.2，分析银行网络角色。银行角色甄别结果如表11所示。

表11 各风险溢出角色之间的溢出关联分析

由表11可知，银行跳跃风险关联网络总共有99个显著关联关系，其中三个群体内部关联数为23，群体之间的关系数为76，表明群体之间存在明显的跳跃风险关联溢出效应。银行角色可以划分为净吸收者、双向溢出者和净溢出者三类角色；净吸收者包括中国银行、建设银行、北京银行、平安银行、招商银行和民生银行，该板块的实际内部关联比例小于预期内部关联比例，而接收关联数高于发出关联数，该群体最容易受到风险信息传染冲击，系统脆弱性较大；双向溢出者包括兴业银行、中信银行、南京银行、浦发银行和宁波银行，该板块的实际内部关联比例高于其预期内部关联比例，且发出关联数与接收关联数均较高，风险传递幅度较高，传染中介作用突出；净溢出者包括工商银行、交通银行和华夏银行，该板块的实际内部关联比例低于预期内部关联比例，但是发出关联数很高且接收关联数较少，属于风险扩散主发源地，系统重要性较高。

密度像矩阵分析结果显示，跳跃风险溢出网络的密度值为0.544，净吸收者的吸收效应体现在各个板块，双向溢出者的溢出与吸收效应主要体现在板块内部以及与净溢出者的关联，净溢出者的溢出效应作用于净吸收者和双向溢出者。

四、研究结论及启示

股价显著跳跃是普遍的，具有时变性、集聚性和杠杆效应等特征，跳跃又显著正向影响股价波动，进一步强化了股票收益率的“尖峰厚尾右偏”等非高斯分布特征，于是，本文选用ARJI-GARCH模型，在一个框架中联合实现跳跃拟合及条件波动率预测，随后修正偏度和峰度，利用一般分析下的风险价值计算式，估算了修正的风险价值，测度银行跳跃风险；随后利用基于VAR模型的广义方差分解技术，构建银行跳跃风险关联度矩阵，计算分析了银行风险溢出与吸收指数及系统性金融风险溢出贡献与风险暴露指数，并做了复杂网络分析。

研究结论与启示归纳起来，有以下几点：

第一，ARJI-GARCH（1,1）模型拟合银行股价条件波动相对更具优势；Kupiec失败比率检验结果表明，计算修正风险价值有效准确程度显著较高。这说明外部冲击会给金融市场带来显著重大的跳跃风险，需要我们动态一致地做好宏观政策调控与金融审慎管理，增强可预见性，创造良好的金融稳定环境，减少并抑制外部冲击，同时有效引导信息、政策、信念与交流，协调稳定市场预期。

第二，仅就银行跳跃风险关联传染而言，建设银行的风险吸收效应最大，其风险净溢出效应也最小，而交通银行风险溢出最大，系统重要性强，风险吸收最小，其风险净溢出效应第二。招商银行的系统重要性较强，华夏银行和南京银行比较脆弱。从风险传染扩散能力和接受能力看，平安银行和浦发银行的系统风险贡献最大，建设银行、华夏银行和南京银行的系统风险暴露较高，位于前三。银行风险传染有溢出和吸收之分，立足微观个体防控系统性风险，就要“强身健体”，树立主动合规、审慎稳健经营的风险文化，深入推进金融供给侧改革，改善金融供给的质量和效率，有序释放存量金融风险，夯实资本实力，增强风险缓释和抵御能力，减少风险溢出传染。

第三，综合考虑出入度数及关联银行重要性三维信息，浦发银行、兴业银行、中信银行、南京银行的出特征向量中心度最大，最容易发出网络最广泛最强传染。华夏银行、宁波银行的等级度最高，运用风险网络结构洞的能力最强。工商银行、交通银行和华夏银行为风险主要溢出者，为系统重要性银行。双向溢出者角色有兴业银行、中信银行、南京银行、浦发银行和宁波银行五家银行，受到外部传染的同时也扮演着溢出的角色，在风险溢出关联中起到了“中介”的作用。净受溢者有中国银行、建设银行、北京银行、平安银行、招商银行和民生银行，系统脆弱性较大。银行角色不同，其在系统性金融风险形成演化中的作用不同，守住底线就要按照银行角色实施分类治理。风险溢出者银行是银行业系统性金融风险的源头所在，应当参照系统重要性银行的附加监管要求，实施附加资本要求、附加杠杆率要求、TLAC总损失吸收能力要求及特别处置机制等，对于具有系统重要性的风险溢出者银行，还可以附加额外监管，如流动性管理、大额风险暴露、业务许可等。风险净受溢者银行是银行业系统中最为脆弱的机构所在，应当全面加强微观审慎监管，促使这类银行强化风险治理，拓展资本补充渠道，创新资本工具和非资本债务工具，提升外部风险总损失吸收能力，实施银行总损失的缓释和吸收能力监管。