基于MATLAB 的多连杆压力机杆系设计系统研究
黄建民,仲 君,夏德琛
(扬力集团股份有限公司,江苏 扬州 225104)
多连杆压力机工作可靠,性能优良,滑块工作速度低且平稳,能很好地满足板料拉延成形工艺要求。因此在拉伸加工领域,多连杆压力机应用广泛,通过配置传动杆系,可以灵活实现多种设计要求。通常这些设计要求可以归纳为以下三种问题:①满足预定的运动规律要求;②满足预定的连杆位置要求;③满足预定的轨迹位置要求[1]。以往为满足设计要求通常都是采用函数逼近法,但计算复杂,并当机构的设计参数较少时,逼近精度不高。若采用最优化方法对机构进行设计,解析目标函数趋势,结果精度高,但需进行大量的数学运算,一般需借助电子计算机来完成[2]。随着计算机辅助数值解法的发展,特别是MATLAB 软件的引入,解析综合法已经得到了广泛的应用[3]。MATLAB 是Mathworks 公司于1982 年推出的一套功能强大的工程计算软件。广泛应用于自动控制、机械设计、流体力学和数理统计等工程领域,被誉为巨人肩上的工具。工程人员通过使用MATLAB 提供的工具箱,可以高效求解复杂的工程问题[4]。本文主要阐述多连杆机构设计的思路与方法,包括建立机构数学模型,使用MATLAB 优化工具箱,编写设计系统,计算所求杆长度,使压力机滑块在多个约束条件下满足预定运动轨迹。
1 建立机构原理模型
图1 为该压力机的杆系机构简图,其中,P1为曲轴中心点,P2为曲柄L2与连杆L3连接点,P3为连杆L3与摇杆连接点,P4为摇杆与机身连接点,P5为摇杆与短连杆L6连接点,P6为短连杆L6与滑块连接点。摇杆前段为L5,摇杆后段为L4,摇杆与水平方向夹角为θ4,P1与P4为机身上的两点连接线长度L1,其与水平方向夹角为θ1。曲柄L2与水平线夹角为θ2,连杆L3与水平线夹角为θ3。摇杆后段L4与连杆L3夹角为θ5,摇杆前段L5与短连杆L6夹角为θ6,短连杆与垂直方向夹角为θ7。
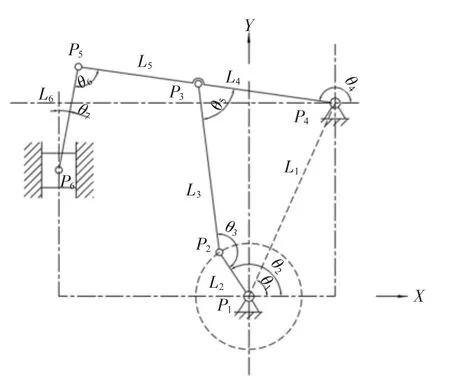
图1 机构原理图
该多连杆为增行程机构,相比普通曲柄压力机,在体身尺寸不变的情况下,可以用较小的曲柄偏心获得更大的行程。压力机要求滑块行程220mm,滑块距下死点90mm 时需能承受300kN 的力,滑块距下死点60mm 时摇杆处于平行状态。根据机身结构配置的限制,有部分参数已给出,以曲轴颈中心点P1为原点,建立笛卡尔坐标系,设各点Pn 的横纵坐标为(Xn,Yn),滑块中心P6横坐标X6=-550,机身点P4横坐标X4=250。摇杆总长为800mm 即L5+L4=800mm,曲柄长为55mm。其中机架间距L1连杆L3,摇杆后段L4均为设计变量,需要通过合理设计L1,L3与L4的长度来达到设计要求。
本案例采用MATLAB 提供的优化工具箱中“函数模块fmincon”来实现三个未知杆长的设计。该函数模块fmincon 需建立目标函数方程及约束函数方程,两种函数方程可以是线性与非线性的等式或不等式[5]。本案例中,目标函数为符合预定杆系轨迹德的最小化方程,约束函数为条件不等式组成的矩阵。
1.1 杆系位置方程组
分析图1 可知,该机构由两部分构成:曲柄L2,连杆L3和摇杆后段L4构成曲柄摇杆机构。摇杆(L4+L5),短连杆L6和滑块P6构成摆动滑块机构。为设计合理杆长满足要求滑块运动轨迹要求,需要建立所求杆与滑块位置的关系方程。摇杆为曲柄摇杆机构的输出杆,也是摆杆滑块机构的输入杆,这样可先解析曲柄摇杆,得出摇杆位置状态,再代入摆动滑块机构求解滑块位置。如图一建立坐标系,以曲轴中心为原点,按杆组法建立方程。
曲柄摇杆机构位置方程为:
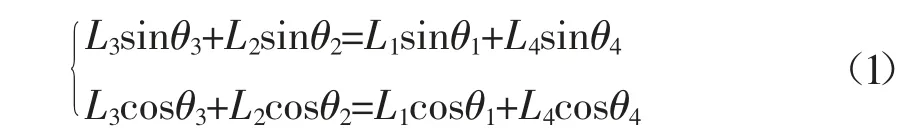
转化为非线性超越方程:
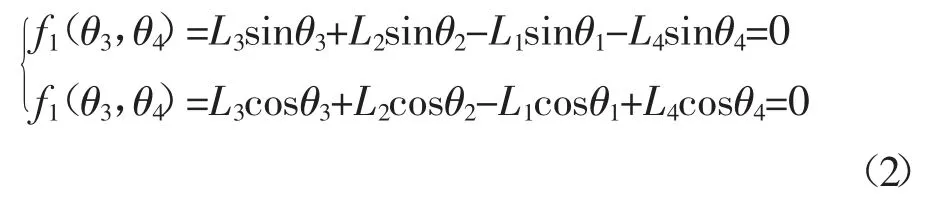
摆动滑块机构位置方程为:
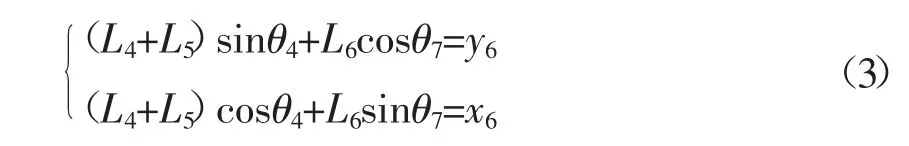
其中(x6,y6)为P6点坐标,x6=-550,L4+L5=800,L6=250,当曲柄位置方程(2)被解出后θ4也为已知,代入(2)求得θ7和y6。
压力机持续工作时,曲柄转角作360°圆周运动,滑块y 方向坐标(y6)随曲柄角度变化而变化,为满足行程220mm 的要求:
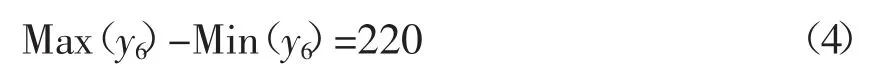
1.2 目标函数
本案例中,建立目标函数的最小化求解问题,计算最优解L1,L3取得理想P5点与实际P5点距离的平方差最小值。
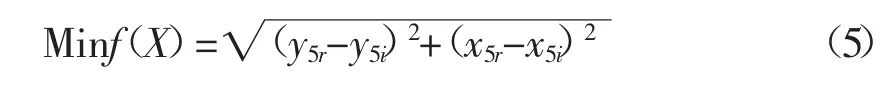
其中(x5r,y5r)为滑块中心P5距下死点90mm 时杆系的实际位置,(x5i,y5i)为滑块中心距下死点90mm 时摇杆水平应有的位置。
1.3 约束条件方程组
该机构的约束条件分为边界约束以及功能约束。其中边界约束包含杆长限制约束,曲柄摇杆机构构成条件的约束,功能约束包括滑块行程约束,摇杆摆动角范围的约束和曲轴可承受扭矩的约束。本案例中程序利用L4作循环语句来求得符合行程的L4,因此不建立滑块行程约束方程。
1.3.1 曲柄摇杆的构成条件
根据机械原理中四杆机构的分析,列出不等式:
L1≥L2,L3≥L2,L1+L2≤L3+L4,L3+L2≤L1+L4,L4+L2≤L1+L3,
以上为曲柄摇杆存在的基本条件,L4与L2为已知不需要列函数方程。对应约束函数为:
g1(X)=L2-X1
g2(X)=L2-X2
g3(X)=L2+X2-X1-L4
g4(X)=L2+X1-X2-L4
g5(X)=L4+L2-X1-X2
1.3.2 摇杆的摆动角约束
如图1,在滑块受力时,杆系受力有θ5和θ6两个压力角,为同时限定两个压力角大小,摇杆的摆动角度θ4需在155°~190°之间。当L2与L3共线时可取摇杆摆动角度的最大及最小值,现以该条件建立方程不等式:
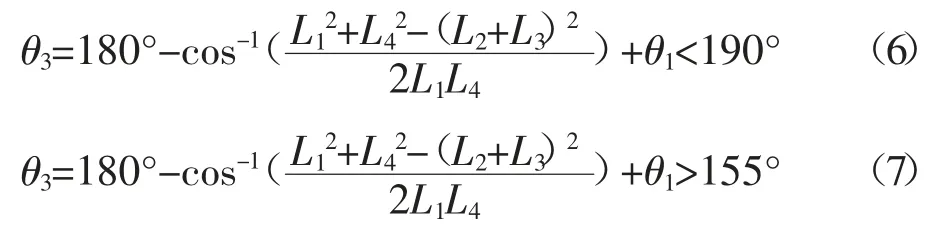
对应约束函数为:
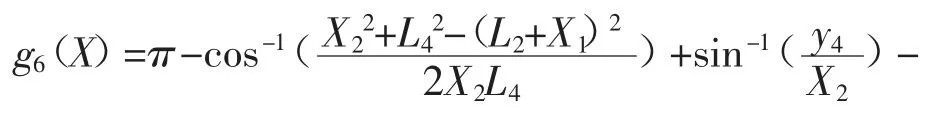
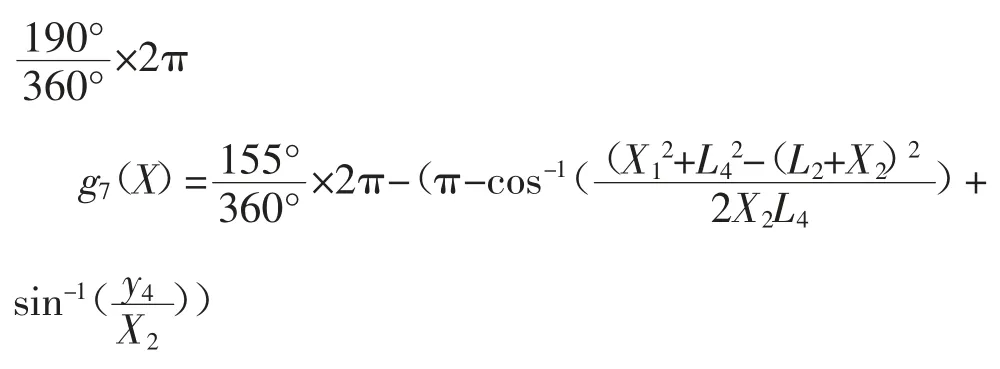
1.3.3 满足曲轴强度要求扭矩
压力机在滑块距下死点90°时开始拉伸,拉伸力F 为300kN。如图2 所示,此时滑块所受的拉伸力经杆系传到至曲轴上,分析曲轴受力可发现曲轴即受弯矩也受扭矩曲轴[1]。本案例压力机用以深拉伸,受力工作行程大,工作时曲柄转角距下死点角度很大,因此主要约束曲轴所受扭矩小于曲轴许用扭矩[τ]=40000Nm。压力机工作时,曲轴扭矩Ttotal一般由理论扭矩Ti和摩擦扭矩Tf组成。理论扭矩即为滑块受力传递至曲轴形成,摩擦扭矩由驱动压力机各配合摩擦阻力形成[6]。
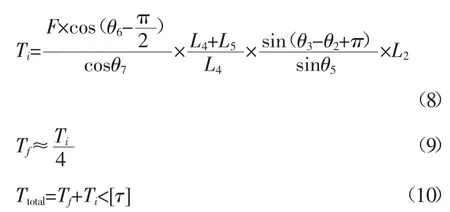
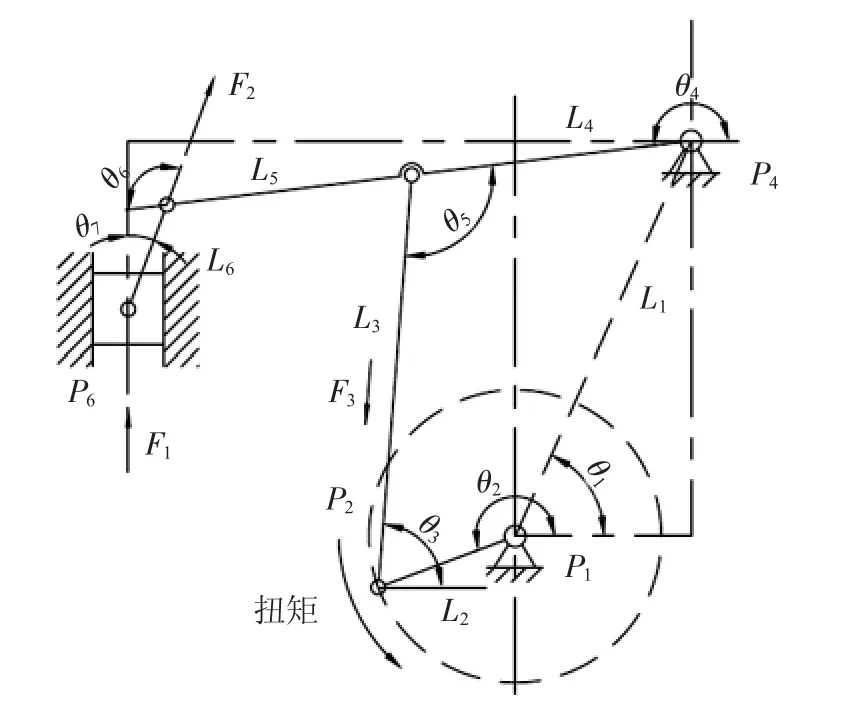
图2 杆系受力传递
2 MATLAB 程序的实现
杆系长度未知的情况下,本案例滑块行程表与曲柄转角的对应关系并不确定,因此无论是目标函数还是约束函数都需要对整个机构位置进行解析计算后才能求解,杆系的两组位置方程组为非线性超越方程,MATLAB 优化工具集中另一个“函数模块fsolve”可以求解此类问题。
2.1 建立目标函数程序
首先名为targetfun.m 的目标函数文件,设定初始条件:
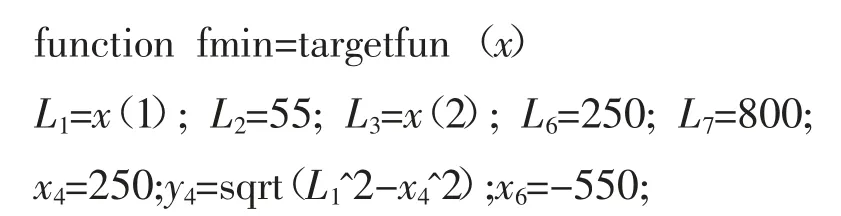
建立摇杆后段的循环语句,计算出合适的L4长度使得滑块行程为220:

建立曲柄转角θ2共360°的循环语句,步长0.5°,调用fsolve 工具解析每一步杆系机构位置状态:


确定上死点,下死点,行程60 的曲柄转角:

最后建立最小化的目标方程:
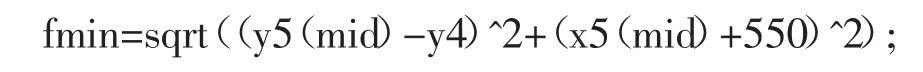
2.2 建立约束函数
建立名为confun 的约束方程模块,根据式(6)~(9),设定初始条件:
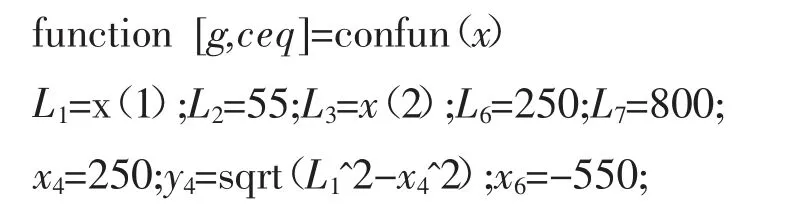
建立摇杆后段的循环语句,计算出合适的L4长度使得滑块行程为220:


建立曲柄转角θ2共360°的循环语句,步长0.5°,调用fsolve 模块解析每一步杆系机构位置状态:

确定上死点,下死点,行程90 的曲柄转角:


列出曲轴存在边界条件:
g(1)=-x(1)+L2;
g(2)=-x(2)+L2;
g(3)=x(1)+L2-x(2)-L4;
g(4)=-x(1)+L2+x(2)-L4;
g(5)=-x(1)+L2-x(2)+L4;
摇杆转角约束:
g(6)=-(pi-acos((L1^2-(L3+L2)^2+L4^2)/(2*L1*L4))+th1)+(155/360*2*pi);
g(7)=pi-acos((L1^2-(L3-L2)^2+L4^2)/(2*L1*L4))+th1-(190/360*2*pi);
最大扭矩限制约束:
g(8)=fttotal-40000;
“哦……”两个人见我如此诚恳,一时间不知说什么好。尴尬了一会儿,服务员赶紧从腰里摸出《收银票据》递给我。我摘下眼镜一看,果然是我消费的内容,价格是43元,而且票据上还手工写着两个字:“未付”。
2.3 构建位置状态模块
调用“fsolve 模块”结合使用杆系的状态方程,根据式(2)建立名为“fourbarposition”的解析模块:
function t=fourbarposition(th,th2,L2,L3,L4,L1,th1)
t=[L2*cos(th2)+L3*cos(th(1))-L4*cos(th(2))-L1*cos(th1);
L2*sin(th2)+L3*sin(th(1))-L4*sin(th(2))-L1*sin(th1)];
3 本方案实例
3.1 设计系统实际使用
本案例中给定连杆和机架长度初始条件为连杆长度700mm,机架距离600mm,其他条件已知。
在计算程序中输入指令。输入初始连杆长度,初始机架长度:x0=[650,700];连杆机架长度的下限约束:lb=[550,500];连杆机架长度的上限约束:ub=[700,700]。
同时,设置函数选项,变量,目标函数,条件函数的调节参数:
options=optimset(“algorithm”,“active-set”,“display”,“off”,“TolFun”,0.001,“TolX”,0.001,“TolCon”,0.001);
图3 为初始杆系与设计后杆曲柄转角与滑块行程的对比图,两条曲线轨迹十分接近。可见在行程一定的情况下,本案例所求两杆的长度变化对曲柄转角与滑块行程关系影响不大。由于其偏置的特性,下死点时曲柄转角都大于180°。图4 为初始杆系与设计后杆系滑块行程与摇杆摆角对比图,其中0 位为下死点位置,可以发现计算后的杆系的摇杆摆角在距下死点60mm 行程时接近180°,符合设计要求,且相比初始杆系,摇杆在工作行程内更加接近水平线。
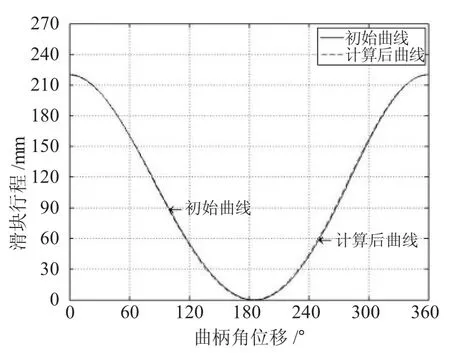
图3 曲柄转角与滑块行程对比
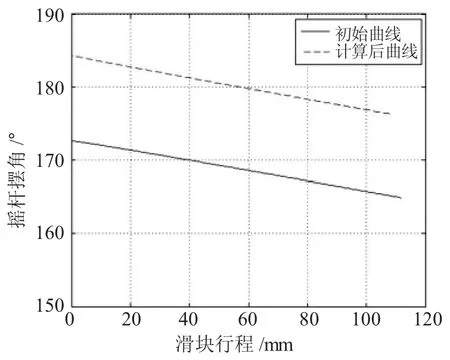
图4 滑块行程与摇杆摆角对比
3.2 设计生产应用
将计算结果应用到设计环节中,并生产出对应的样机,如图5。并随之测试各方面性能,对比初始计算目标。首先,完成任务目标,即建立杆系传动系统,保证样机的传动系统很大的工作行程下承受足够的扭矩;其次,为限制机床整体尺寸大小,杆系长度保证在满足设计目标情况下缩小长度,在设计系统中限制相关参数,并将结构排至紧凑,如图6 所示;最后,对于专用机床,性能参数根据整体而确定,因此生产量不大,合理利用设计系统,搭建成熟的平台,同类型的机床小幅修改杆系长度以达成要求。

图5 多连杆样机
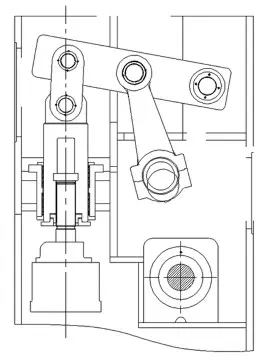
图6 样机传动简图
4 结论
多连杆压力机杆系设计往往比较复杂,除了要满足杆系预定轨迹要求外还考虑压力机实际功能的设计要求。本案例使用基于MATLAB 的设计系统实现杆系设计,其计算结果体现MATLAB 的一大优势在于数据处理运算非常方便,在优化设计时建立数学模型,调用多样的函数工具集进行分析计算,过程中产生的计算数据便于性能分析或图表绘制,并产生结果应用到实际设计生产过程中去。本案例方法具有进一步发展的潜力,通过建立不同的目标函数方程,还可以实现杆系总体重量最小化设计等设计要求。有些多连杆压力机要求拥有特殊的滑块轨迹或运行曲线,通过对位置方程的求导,得到速度方程或者加速度方程,可以将滑块速度或加速度加入数学模型中。这样用类似的解析方法也能对此类型的多连杆压力机进行杆系设计。

