通风压力及泄露位置对燃料电池汽车氢气小孔泄露的影响
高 源,陈朝刚
(1.同济大学新能源汽车工程中心,上海201804;2.同济大学汽车学院,上海201804)
随着化石燃料资源逐渐消耗,国家能源战略逐步推进,氢能源的发展越来越受到重视。与此相应,汽车产业也在全球范围内经历一场能源革新,欧盟许多国家提出了汰换内燃机的具体时间点,用新能源汽车代替传统产品,因此新能源产业得到了极佳的发展机会。然而,机遇出现的同时必然伴随着不容忽视的挑战,截至2018年中国的燃料电池汽车发展水平还没有跻身国际第一梯队,车载储氢技术、氢安全方向仍存在不足[1],理论和实践都有待进一步提升。
在评估汽车氢能源系统的整体安全性时,氢泄漏安全的评估不容忽视。氢气泄露又可以根据氢气泄漏源和周围环境大气压之间压力比值的不同,分为亚声速射流和欠膨胀射流。在泄露口亚声速射流已经充分膨胀,压力与周围环境压力相等,气流速度低于当地声速,泄露后的氢浓度分布满足双曲线衰减规律[2];欠膨胀射流在泄漏口的速度等于当地声速,出口外射气流继续膨胀加速,氢浓度分布也更加复杂[3]。
小孔泄露是气体泄露的一种形式,欧洲输气管道事故数据组织(EGIG)将泄露孔径d≤20 mm的情况定为小孔泄露,满足20 mm<d<D为大孔泄露(D为管道直径)[4]。杨昭等[5]提出了小孔是否为小微孔由管道直径D和孔径d共同决定。冯云飞等[6]将d/D≤0.2的归结为小孔泄露,0.2<d/D<0.6的为大孔泄露,d/D≥0.6的为管道断裂,并详细阐述了d/D≤0.2时采用小孔泄露模型的合理性。
当气体发生泄漏时,主动通风有助于氢气的快速逸散。Matsuura等[7]建立了泄漏模型,计算了单个泄漏点情况下氢气在房间内的分布,并研究了不同通风压力下房间内氢气浓度的分布规律。Li等[8]和Mao等[9]借助Fluent软件研究了氢燃料电池船舶氢气泄露时氢气在船舱内的分布情况,以及主动通风和自然通风条件下船舱内危险区域的分布情况。Qian等[10]等采用Fluent软件,研究了氢气泄露在加氢站内发生时氢气的分布规律,以及自然通风对氢气聚集特性的影响。李静媛等[11]使用基于流体力学的Flacs软件模拟了上海世博加氢站内氢瓶泄露并爆炸的情况,研究了不同环境风速对高压氢气泄露爆炸事故的影响规律。李云浩等[12]和Choi等[13]采用计算流体动力学软件建模,在车库内氢气连续性泄漏的条件下,分析了车库结构以及通风对氢气浓度分布和聚集状态的影响。Hajji等[14]研究了半封闭空间中通风口的形状和大小对可燃氢-空气云形成的影响。Bie等[15]对隧道中氢气的泄露事故进行了研究,得到了隧道通风速率和隧道内可燃氢气云团间的关系。以上所述的主动通风系统主要应用于质子交换膜燃料电池车辆的外部,关注点在于主动通风对外环境中氢气泄漏的影响,对车辆内环境中氢气泄露以及通风与氢气浓度分布相关关系的研究较少。
仿真软件作为流体研究的重要工具,在氢气泄露过程中也得到了广泛应用。刘延雷等[16]基于Fluent软件的物质传输与反应模块,建立了燃料电池汽车内氢气泄露扩散的数值模型,描述了二维平面内氢气泄露扩散后危险区域的分布情况。余亚波等[17]建立了氢气泄露的三维仿真模型,研究了燃料电池汽车发生氢泄漏时,通风格栅面积以及通风格栅设置方式对车内氢气浓度的影响。卢明等[18]建立了三维仿真模型,研究氢气在储氢室中的泄漏情况以及通风对氢气泄露的影响。郑津洋等[19]使用Fluent软件研究泄露口障碍物与泄露点距离对氢气分布的影响,障碍物距离越远氢气在水平方向上的分布就越广泛。李雪芳等[20]建立了氢气分层流动模型,将氢气射流激波结构纹影图像和仿真结果进行对比,两者具有很高的相似度。
基于稳态小孔泄露方程建立氢气泄露的准静态模型,对氢气泄露进行模拟。建立二维仿真模型,探究车内发生氢气泄露时氢气浓度的分布,以及通风对氢气泄露的影响。
1 理论基础
氢气泄漏事故中氢气泄漏过程是否可控是一个重要指标,可以通过数学模型模拟氢气泄漏过程中物理量变化,从而对氢气泄漏事故的可控性进行评估。为了得到氢气泄漏过程中质量流量的数值变化特征,将泄露过程中氢气的泄漏点抽象为小孔,探求储氢罐容积、氢气压力、氢气温度对氢气质量流量的影响。作如下假设:
(1)由于小孔的尺寸相对于容器很小,因此在一个较小的时间段Δt内气体处于稳定状态。
(2)在每一个Δt内,不考虑容器的传热损失,泄露行为假设成等熵流动。
(3)在喷嘴处氢气的流动假设为绝热膨胀。
考虑高压气体物理性质对理想气体的偏离,在计算氢气喷嘴的气体状态时假设气体为绝热膨胀。Noble-Abel实际气体状态方程为
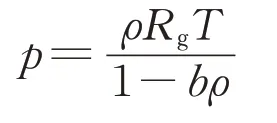
式中:p、ρ、T分别为气体的压力、密度和温度;Rg为气体状态常数;b为与气体种类有关的常数,对于氢气,b=0.007 691 N·m-2。绝热膨胀过程遵循以下方程:
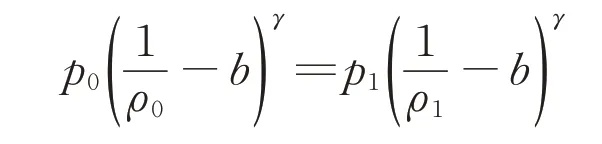
式中:γ为气体绝热系数;下标0和1分别代表氢气经过氢气泄漏通道的起始点和终止点。结合气体质量、动量和能量守恒方程,可得
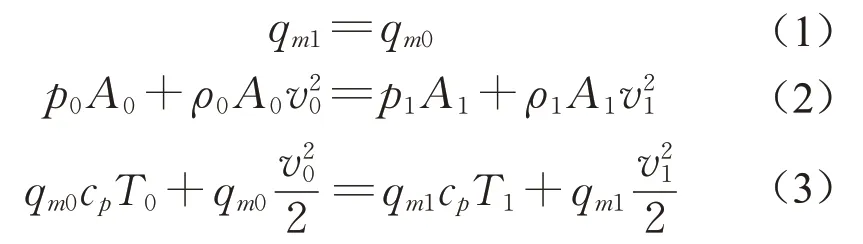
式中:qm为气体的理论质量流量;A为小孔面积;v为气体流速;cp为氢气的比定压热容。联立式(1)~(3),可以得到氢气在泄漏点出口处的初始速度v1。考虑出口处形状,得到可压缩气体通过小孔泄露的实际质量流量公式[21],如下所示:
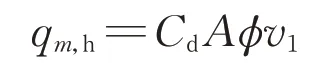
式中:qm,h为氢气小孔泄露的质量流量;Cd为泄露系数,其值由摩擦系数和小孔收缩系数决定,一般来说,圆形孔取Cd=1.00,三角孔取Cd=0.95,长方形孔取Cd=0.90;φ为气体流动系数。当外界大气压力和容器内气体压力之比小于气体临界流动压力比β时,气体泄露过程为临界流动,取φ=1;当压力之比大于β时,φ通过下式确定:
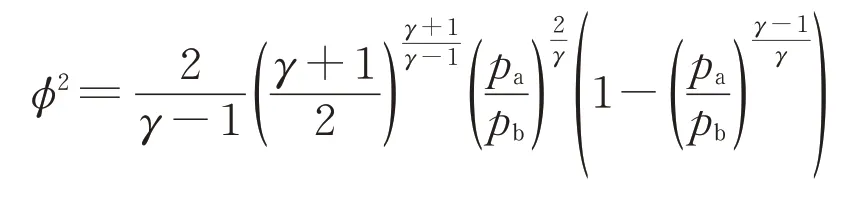
式中:pa为外界大气压力;pb为容器内气体压力。气体临界流动压力比β可以根据下式获得:
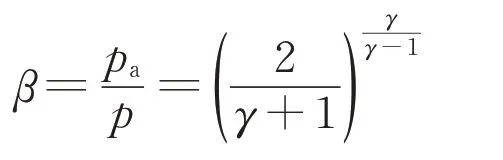
获得气体的质量流量后,可以根据下式计算容器内气体的密度变化:

式中:ρi、ρi+1分别为第i个和第(i+1)个时间步长时的气体密度;V为容器容积;qmi为第i个时间步长时的气体质量流量。
气体的泄漏是等熵过程,根据理想气体等熵膨胀方程计算容器内的压强和温度,如下所示:
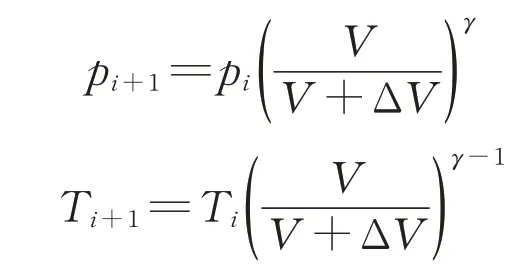
式中:pi、pi+1分别为第i个和第(i+1)个时间步长时的气体压力;Ti和Ti+1分别为第i个和第(i+1)个时间步长时的气体温度;ΔV为一个时间步长内泄漏的气体体积。ΔV通过下式确定:
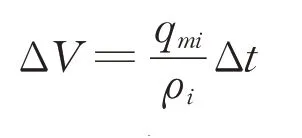
根据以上计算过程,建立了Matlab/Simulink仿真模型,计算逻辑图如图1所示。在此模型中设置4个模块,分别实现初始条件设置、实时数据记录、下一时间系统状态计算、结束条件判定。在计算的每一步中,将系统模型近似看作稳态,计算系统在Δt之后的压力、温度等状态值,并将得到的新值代入模型进行迭代计算。
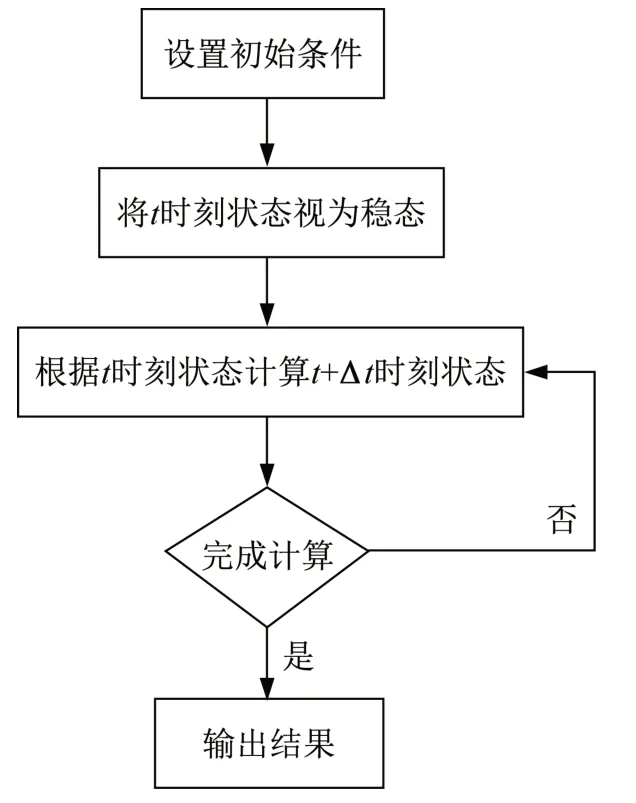
图1 Simulink流程Fig.1 Flow chart of Simulink
采用该模型模拟了储氢压力为70 MPa的氢瓶(15.6 L)通过直径6 mm小孔的泄漏情况,各参数的初始取值如表1所示。

表1 仿真初值Tab.1 Initial value of simulation
2 氢气质量流量影响因素
氢气泄漏过程中质量流量最具有代表性,观察质量流量的峰值以及随持续时间的变化能够看出泄露过程的整体特征。通过改变该物理系统中的参数值,观察质量流量随之发生的变化,探求该物理量对质量流量的影响。
在质量流量曲线中,曲线下方面积即为泄漏氢气的质量。
(1)储氢罐容积V
从图2可以观察到,随着时间的持续,质量流量逐渐变小,但是小容积储氢罐质量流量下降更快,也更快到达零点。
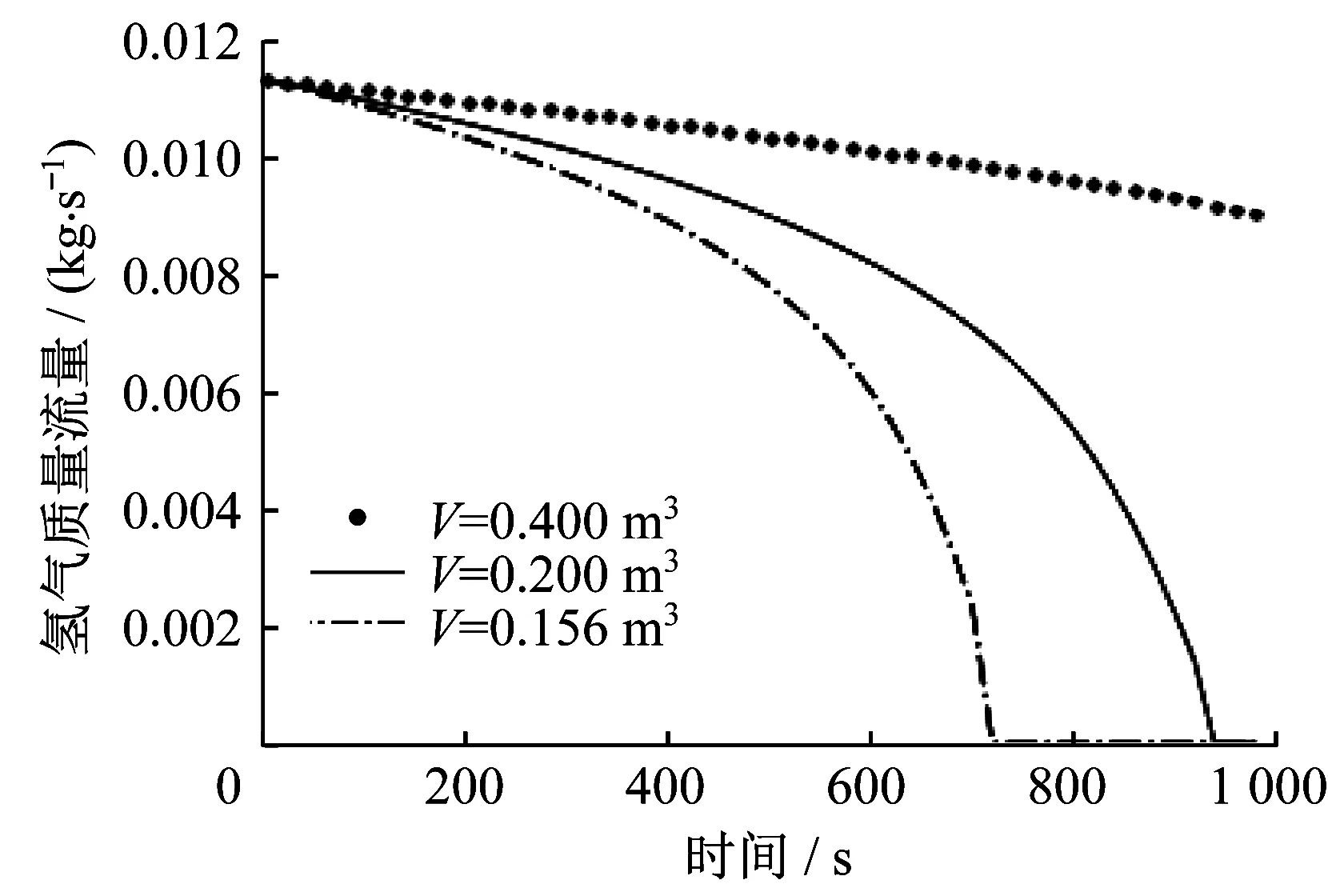
图2 不同储氢罐容积下质量流量随时间变化Fig.2 Mass flow rate versus time at different hydrogen tank volumes
小容积储氢罐的氢气泄漏量有限,若在泄漏发生的时间段内通过主动监测发现泄漏,并及时切断氢气供应使系统停止氢气泄漏,则氢气泄漏量远低于大容积储氢罐。在仅考虑储氢罐泄露的情况时,使用多个小容积储氢罐可以减小由单个大容积储氢罐泄漏造成的安全隐患。单个大容积储氢罐的氢气泄漏安全性低于多个小容积储氢罐。
(2)储氢罐外界温度Tw
如图3所示,4条曲线没有明显差异,随着温度的变化,氢气泄漏特性几乎没有发生变化。因此,从氢气泄漏安全角度,极热或极冷天气对氢气泄漏的影响并不大。考虑到高温可能会影响氢单质的化学活性,高温使泄漏出的氢单质更容易与氧气反应而扩大泄漏点,使泄漏事故更严重,所以仍需进一步评估质子交换膜燃料电池的散热性能。

图3 不同温度下质量流量随时间变化曲线Fig.3 Mass flow rate versus time at different temperatures
(3)储氢罐压力ps
从图4观察到,高压储氢系统在泄漏初始状态下达到更高的氢气质量流量,而低压储氢系统初始质量流量明显低于高压储氢系统。尽管高压储氢系统的质量流量表现出了更快的下降趋势,前几秒内其质量流量还是明显高于低压储氢系统。
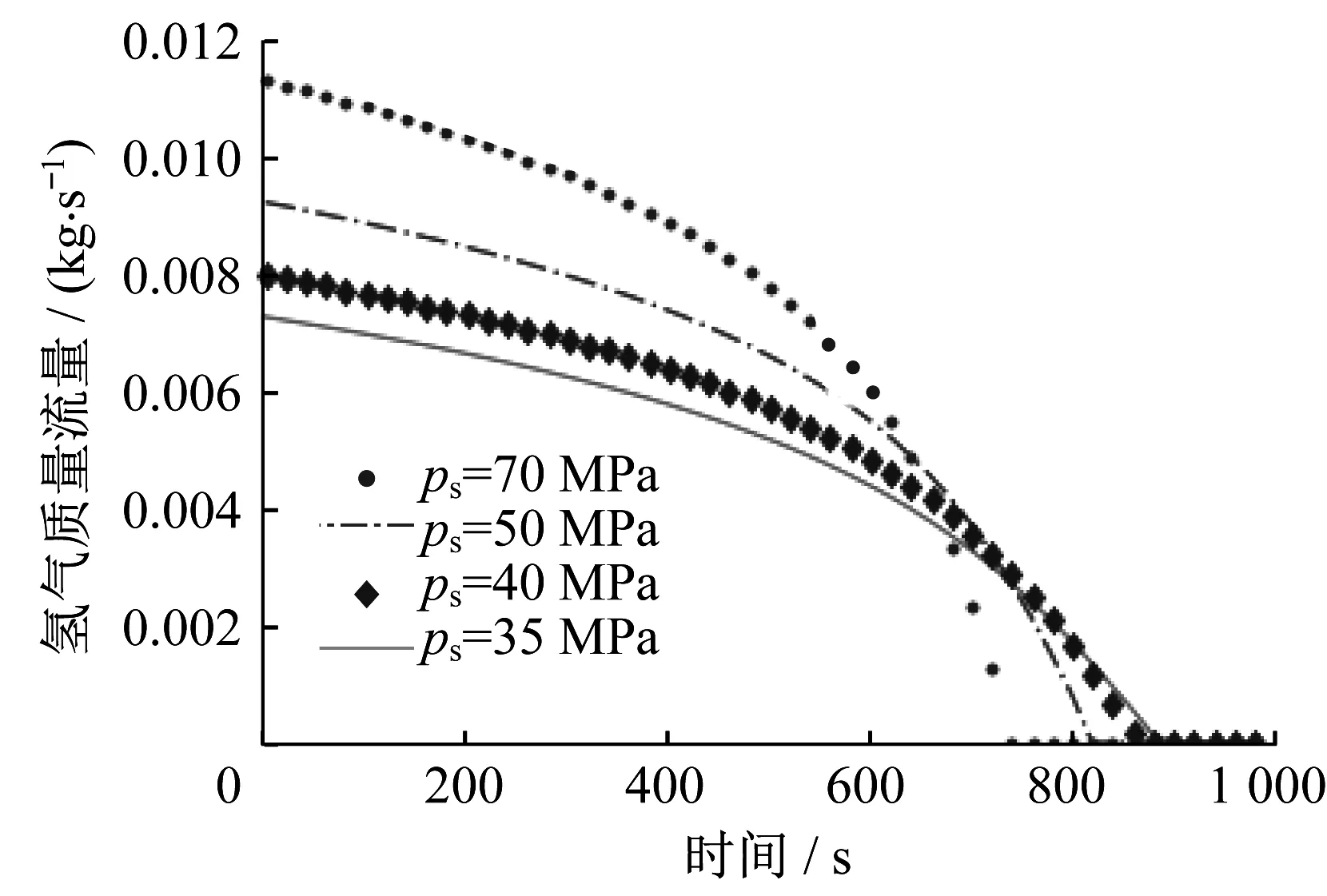
图4 不同储氢罐压力下质量流量随时间变化Fig.4 Mass flow rate versus time at different hydrogen storage pressures
高压储氢系统在泄漏事故中向外界释放更多的氢气,从而高压储氢系统拥有高于低压储氢系统的危险性。在要求单位体积氢气能够多做功的发展趋势下,高压储氢为大势所趋,但是与高储氢压力相对应的是更大的泄漏风险。氢气泄露的风险管控应该保证质子交换膜燃料电池在应用过程中的安全性,并且在泄漏事故发生后,做到尽量减小泄漏事故对人身财产安全的威胁。
3 计算流体力学仿真
为了保证使用过程中的安全性,质子交换膜燃料电池汽车通常需要在车内合适的位置布置氢气传感器,用于探测车内氢气的浓度。因此,有必要对氢气泄露时车内的氢气分布进行仿真,研究泄露点位置以及泄漏点通风情况对车内氢气分布的影响。常用计算流体力学软件模拟氢气的泄露和扩散。
3.1 数值模型
氢气在泄漏扩散的过程中不断与环境中的空气混合,形成湍流扩散。在扩散过程中气体连续流动,质量和能量守恒,而且各组分的分布满足组分输运方程。基本控制方程[17]如下所示:
(1)连续性方程

式中:ρg为混合气体密度;x为主风向坐标;下标i表示第i个组分。
(2)动量方程

式中:pg为静压力;Tij为偏应力张量;G为重力。
(3)能量方程
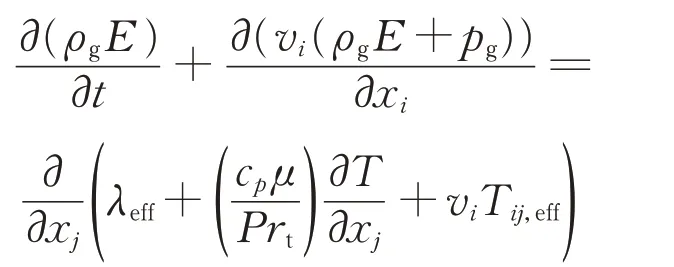
式中:E为气体总能;λeff为有效导热系数;μ为湍流黏度;Prt为湍流普朗特数;Tij,eff为有效偏应力张量。
(4)组分输运方程
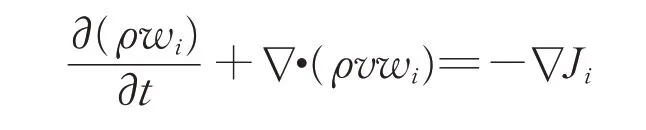
式中:wi为组分i的质量分数;Ji为组分i的质量扩散速度。
Realizablek-ε湍流模型能够对含有射流和混合流的湍流流动进行准确模拟[22]。因此,在小孔泄露计算流体力学仿真中,选择Realizablek-ε湍流模型对氢气的泄露过程进行模拟。
3.2 通风压力对车内氢气分布的影响
二维模型可以定性表示氢气在车内的分布情况,根据市场上的常见车型建立了二维平面模型。如图5所示,该车型是某市售SUV,车内空间较大,有足够的空间布置体积较大的氢罐。空气的进口和出口如图6所示。
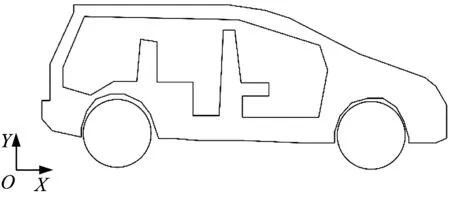
图5 汽车二维模型Fig.5 Two-dimensional car model
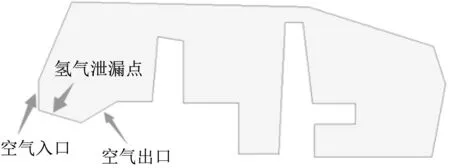
图6 空气进出口Fig.6 Inlet and outlet of the car
在通风口位置,分别对空气入口施加10~3 000 Pa的空气压力。氢气泄露点直径设置为6 mm,与常见氢传输管道的直径相同,泄露处氢气表压力为0.1 MPa。60 s后的氢气分布如图7所示。
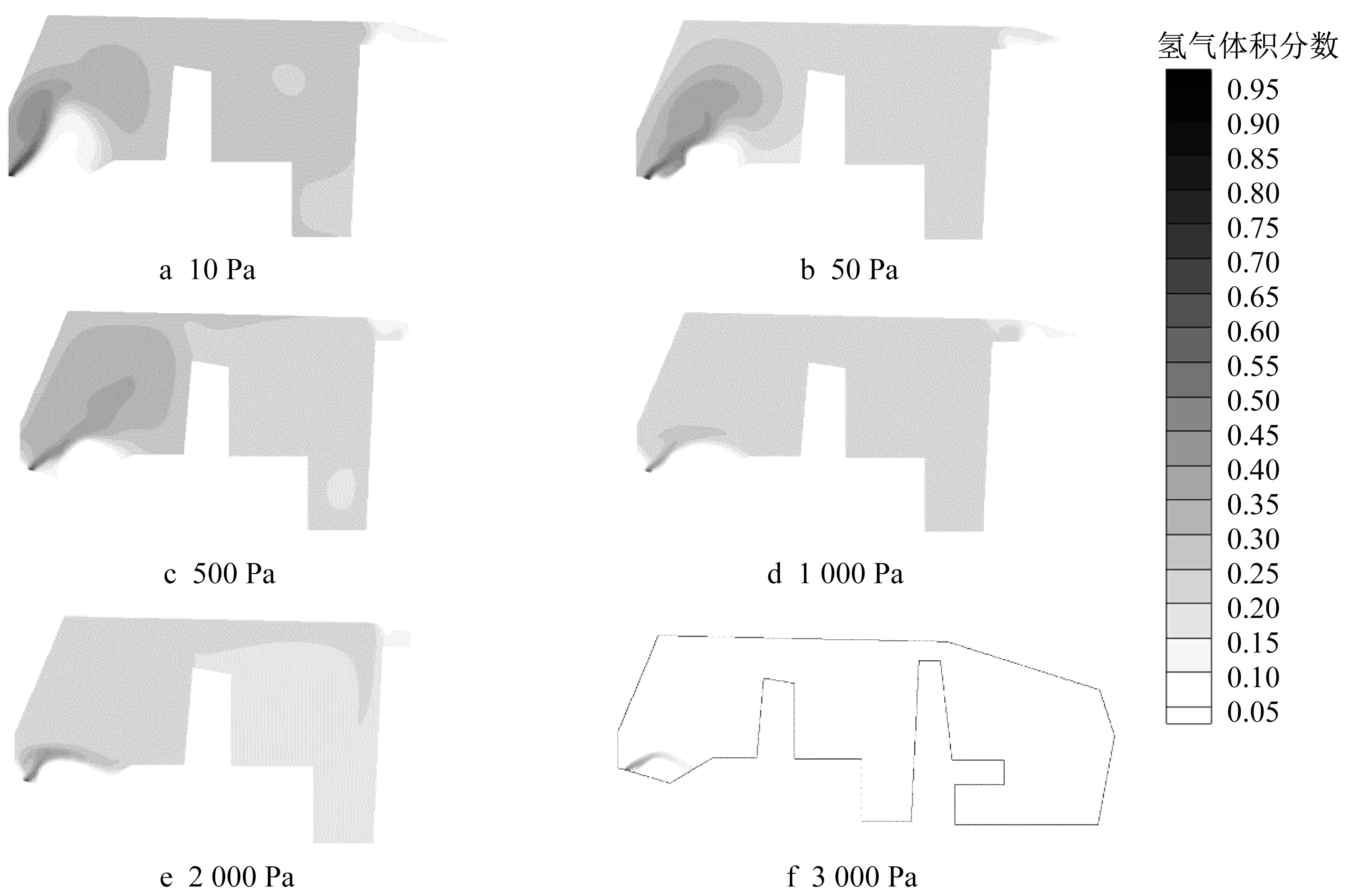
图7 通风风压对车内氢气分布的影响Fig.7 Effect of ventilation air pressure on distribution of hydrogen in car
在不同的通风风压作用下,车内气体呈现出了不同的分布特征。在靠近泄露点的位置氢气浓度较高,离泄漏点越远浓度越低。随着通风压力加大,车内氢气的体积分数也显著降低,在通风压力达到3 000 Pa时效果极为显著,但是小型风扇很难达到这样的通风压力。
此外,由于受到了座椅的分隔,汽车轿厢内部空间被隔成了3个相对独立的部分,并且不同区域之间出现了较为明显的氢气体积分数分布差异。当空气主动通风压力为500 Pa时,车舱的轿厢中段氢气体积分数为0.20~0.25,远离氢气泄露点的轿厢分段氢气体积分数低于0.05,而轿厢靠近泄露点的氢气体积分数普遍高于0.30。
氢气泄漏点的局部通风对减小氢气的扩散有效,但是当高压供氢管路泄漏时,需要极高的风压才能够完全抑制氢气的泄漏,同时供氢管路对风压的承受能力有限。在氢气泄漏压力较小时,较小的风压也可以使氢气泄漏完全被抑制。
3.3 氢气泄露位置对车内氢气分布的影响
对某热销新能源电动车进行测试,设置3个不同的氢气泄露点,分别在车的仪表盘、车前座地板、车后座(见图8),研究氢气泄露位置对车内氢气分布的影响。仿真结果如图9~11所示,氢气泄漏点颜色越接近黑色代表氢气浓度越高。泄露点的直径为6 mm,氢气表压力为0.1 MPa。
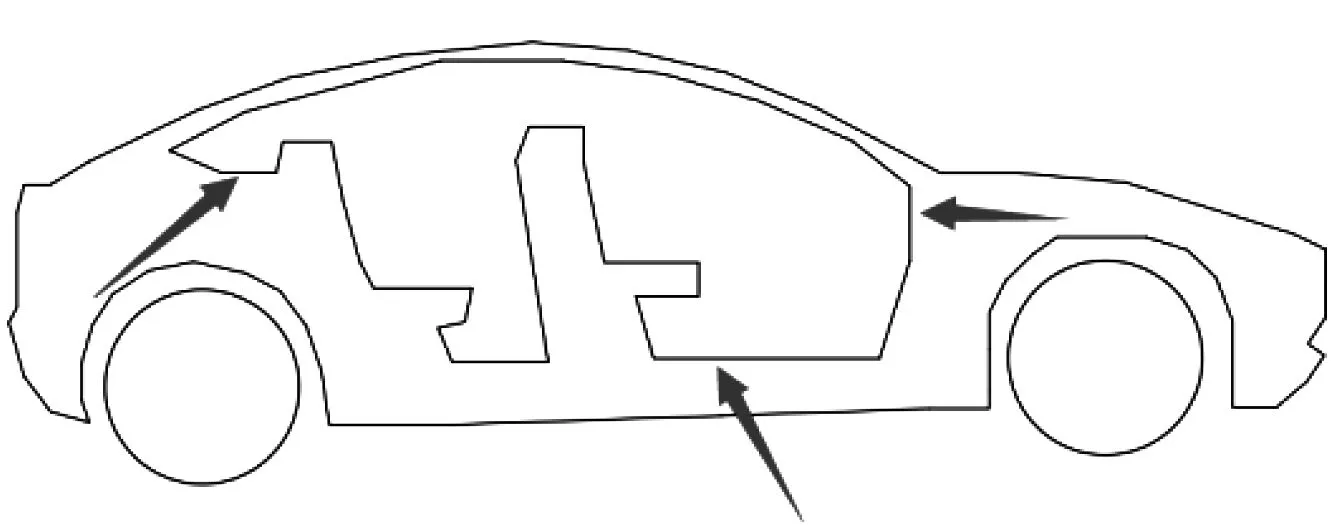
图8 氢气泄露点位置Fig.8 Location of hydrogen leakage point

图9 车尾泄露仿真结果Fig.9 Simulation results of vehicle tail leakage

图10 车底泄漏仿真结果Fig.10 Simulation results of vehicle bottom leakage

图11 车前部泄露仿真结果Fig.11 Simulation results of the leakage at thefront of the car
从图9~11可以看出,离泄露点越近的位置氢气浓度越高,并且车顶更容易聚集大量的氢气。因此,密闭驾驶舱内的氢气检测点应该尽量靠近供氢管路的安装位置,在车顶安装也可以起到不错的效果。
4 结语
采用Matlab/Simulink软件建立了简化的高压氢气小孔泄露数值模型,探究了储氢罐的压力、外界温度和容积对氢气泄露的影响。然后,建立了Fluent二维仿真模型,探究了通风压力对车内氢气分布的影响。
储氢罐容积越小,发生单个氢瓶泄露事故时质量流量下降越快,泄露的氢气总量也更小。储氢罐压力对泄漏时的质量流量也有显著影响,储氢罐压力越高,质量流量的下降速度越快,相同时间内泄露的氢气总量也越大。外界温度对氢气泄露的影响很小,几乎可以忽略不计。
通风风压越高,氢气在乘员舱扩散的浓度就越低,风压高于一定数值时,泄漏的氢气被直接吹入大气。在封闭座舱内,氢气浓度分布随着泄漏点位置以及泄漏点压力的改变而变化,呈现出泄漏点聚集性。若氢气的泄露位置以及泄漏点氢气压力发生变化,则仿真结果会有所不同,在实际设计中需要具体问题具体分析,根据实际情况评判氢气泄露时主动通风的作用。

