装配式新型灌浆套筒接头设计及有限元分析

赵 军 刘 佳 王飞程 朱银红

(1.桂林理工大学 广西新能源与建筑节能重点实验室, 广西 桂林 541004;2.桂林理工大学 土木与建筑工程学院, 广西 桂林 541004)

现浇式混凝土结构在现场施工过程中,所需劳动力大,施工工期长,需要搭建大量脚手架,具有安全系数不高,污染大,施工噪音大等诸多缺点.为解决这些问题,2017年印发的《装配式建筑示范城市管理办法》[1]和《装配式建筑产业基地管理办法》[2]提出大力发展装配式建筑.如今,混凝土结构建筑的发展逐渐从现浇式混凝土结构建筑转变为装配式混凝土结构建筑.装配式混凝土结构作为现阶段建筑行业的主流,关于装配式构件连接节点的研究也逐渐成熟,钢筋灌浆套筒连接技术则是装配式构件连接的关键.

早在20世纪60年代,美国人Alfred A.Yee首次提出灌浆套筒技术,随后在北美、日本、欧洲等地广泛应用到实际工程建筑中[3].为之后的灌浆套筒技术的发展奠定了基础.Jirsa[4]对18个灌浆套筒试件进行了单向拉伸试验,研究了影响套筒极限承载力的因素.2013年吴小宝[5]研究了龄期和钢筋种类对钢筋套筒连接接头受力性能的影响.随后陈洪[6]在已有的试验基础上,利用有限元软件ABAQUS模拟了灌浆套筒的受力性能,有限元模拟结果与试验结果对比吻合,但未考虑粘结滑移破坏.2016 年郑永峰[7-9]等设计了一种新型变形灌浆套筒,即grouted deformed pipe splice(GDPS)灌浆套筒,如图1所示.该套筒由无缝钢管通过三轴滚压机冷压轧制而成,经过单向拉伸、循环荷载试验研究了其连接性能、工作机理等.该套筒表现出良好的力学性能,同时制作工艺简易,大大降低套筒成本.本文将在GDPS灌浆套筒单向拉伸试验的基础上,对试验构件进行有限元模拟分析,与试验结果作对比.再设计多组不同规格的新型灌浆套筒进行有限元模拟分析.

图1 GDPS套筒

1 试验概况

文献[7]中,GDPS灌浆套筒是利用Q390B 无缝钢管通过三轴滚丝机滚压制作而成,钢筋插入套筒并对中后浇筑灌浆料凝固制作成灌浆套筒连接接头.对灌浆套筒连接接头进行单向拉伸试验.接头试件几何构造如图2所示.

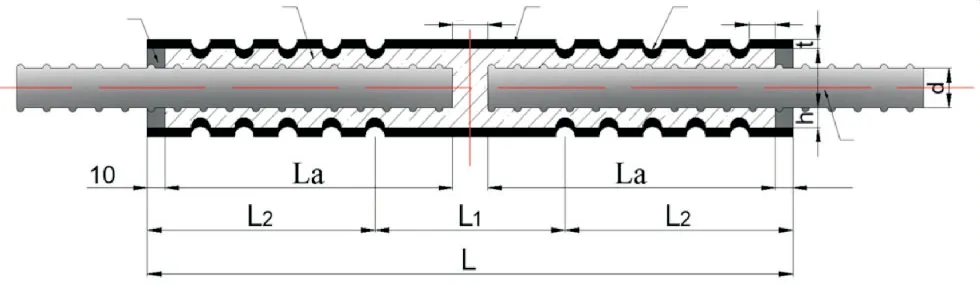
图2 GDPS套筒接头几何构造(单位:mm)

试验部分设计了GB-D25-1和GB-D25-2不同钢筋锚固长度的接头试件进行单向拉伸试验.连接钢筋直径为25 mm,套筒外径为47 mm,套筒壁厚为5 mm,肋深2.5 mm,试件参数及主要试验结果见表1.

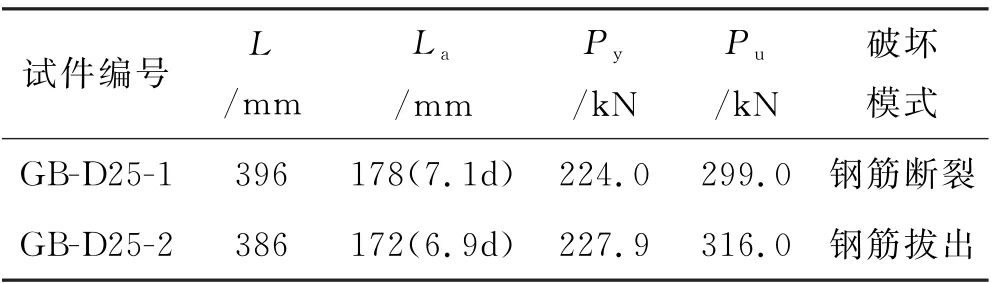
表1 试件参数及主要试验结果

2 有限元模型

2.1 材料参数与本构

2.1.1 钢筋和GDPS套筒

模型使用HRB400 级钢筋,Q390B 无缝合金钢管套筒属性.钢筋和套筒均为理想弹塑性模型,模拟采用二折线模型,材料各参数见表2,应力-应变曲线如图3所示.

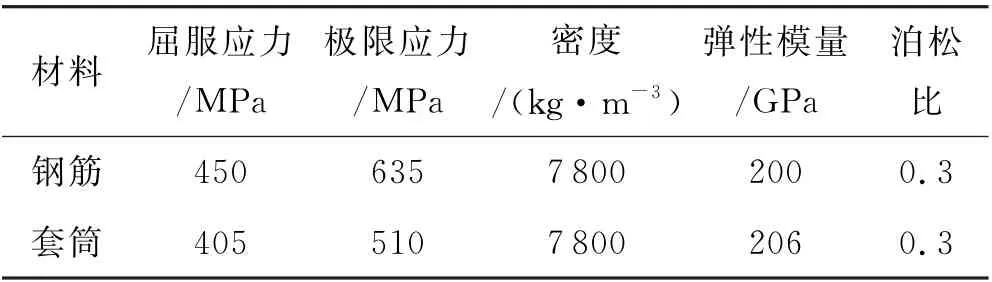
表2 钢筋和套筒材料

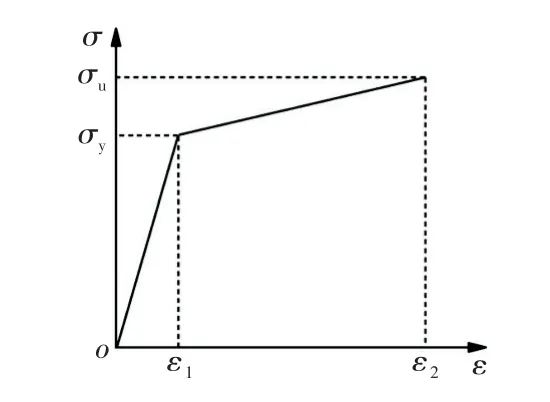
图3 钢筋和套筒本构模型

钢筋的应力-应变关系式:

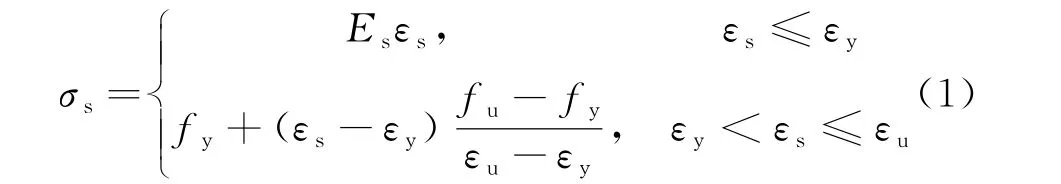
式中:Es为钢筋弹性模量;εs为钢筋应变;σs为钢筋

应力;fy为钢筋屈服强度;fu为钢筋极限抗拉强度;εy为钢筋屈服应变;εu为钢筋极限应变.

2.1.2 灌浆料

灌浆料研究现阶段尚无完整的理论模型,本模型采用C80高强混凝土各向同性混凝土损伤塑性模型(CDP模型)代替高强水泥基灌浆料模型,密度为2 500 kg·m-3,弹性模量为38 GPa,泊松比为0.2.非弹性阶段采用规范[10]中的混凝土应力-应变关系确定.

受拉情况:

式中:αa、αd分别为受压应力-应变上升和下降段参数.

2.2 模型建立

考虑到灌浆套筒接头为轴对称结构,建立2D 轴对称壳单元1/4模型进行分析,这种建模方式的优点在于建模简易,计算速度较3D 实体模型快,大大提高计算效率.分析步采用隐式动力学方法,模型易收敛.相互作用的定义,首先建立一个通用接触,法向作用为“硬接触”,切向作用为库仑摩擦模型,摩擦系数为0.2.利用cohesive单元来模拟灌浆料与钢筋以及灌浆料与套筒之间的粘结滑移模型.ABAQUS中的自带cohesive单元为双线性三角模型,如图4所示.

图4 粘结滑移模型

图中,横坐标轴S为位移;纵坐标轴τ为粘结应力;τmax为极限粘结强度;S1为单元损伤起始时对应的位移;S2为单元彻底失效时的位移.cohesive单元作用时粘结强度线性增长,增至极限粘结强度开始线性下降,直至单元彻底失效,单元失效后由通用接触作用.

粘结滑移模型的表达式:上升段:0≤S≤S1,τ=K1S1;下降段:S1＜S≤S2,τ=K2S2.其中,K1,K2分别为单元上升段和下降段的刚度.

网格划分采用自由网格划分方式,单元主要以四边形为主.由于模型为1/4模型,套筒关于X、Y轴对称.套筒中部X轴方向边界条件为固定约束;Y轴上边界条件为只有向Y方向上滑动的约束,在Y轴方向施加荷载.如图5所示.

图5 边界条件与网格划分

以本节建模方式和表1 参数建立GB-D25-1 和GB-D25-2模型,与试验结果对照.再在试验基础上设计了10个不同参数的套筒连接试件模型,设计钢筋直径d为22 mm,套筒总长度L为350 mm.模型具体参数见表3,模型几何构造图如图2所示.

表3中以模型B7.5d-5-10为例编号的含义:“B”表示套筒的肋个数,为5个,A、C 表示的肋个数分别为4个和6个,“7.5d”表示锚固长度为7.5d,“5”表示套筒厚度为5 mm,“10”表示灌浆料厚度为10 mm.

表3 模型构造参数

3 模型验证与结果

3.1 模型验证

以文中2.1节的材料本构与2.2节建模方式建模得到模拟结果.试件GB-D25-1 和GB-D25-2 的试验与模拟结果都分别是钢筋断裂和钢筋拔出两种破坏形式.其中钢筋断裂试件模型,当钢筋出现颈缩现象达到极限荷载,随后钢筋断裂承载力下降.钢筋拔出试件模型承载力达到极限荷载时粘结力失效钢筋滑移拔出,承载力下降.模型的Mises应力云图如图6所示.

图6 Mises应力云图

试验和模拟结果荷载-位移曲线对比,如图7所示.钢筋断裂(图7(a))和钢筋拔出(图7(b))的模型曲线,钢筋模型为二折线模型,则模拟结果荷载-位移曲线没有屈服平台.强化阶段结束后模型达到极限状态荷载-位移曲线趋势下降,钢筋分别断裂和拔出.钢筋断裂试件模型有限元和试验的屈服荷载分别为222.3 k N 和224.0 k N,钢筋拔出试件模型分别为229.1 k N 和227.9 k N,屈服荷载误差分别为0.76%和0.52%.钢筋断裂试件模型有限元和试验的极限荷载分别为302.2 k N 和299.0 k N,钢筋拔出试件模型分别为310.3 k N 和316.0 k N,极限荷载误差分别为1.06%和1.80%.试验结果与模拟结果基本吻合.

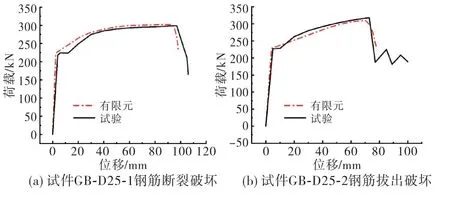
图7 试验结果与模拟结果荷载-位移曲线对比

3.2 设计模型的模拟结果

以表3的模型构造参数、文中2.1节的材料本构和2.2节建模方式对设计的10个套筒连接接头进行有限元模拟,模拟结果见表4.可见,除B7.0d-5-10以外其他模型的接头抗拉强度与钢筋的抗拉强度标准值的比值fu/fbyk＞1.25,与钢筋抗拉强度标准值的比值fu/fbuk≥1.10,满足国内规范[11]中的I级接头以及美国规范[12]中Type2类接头单向拉伸强度要求.

表4 模拟结果

对于不同锚固长度的模型B7.0d-5-10、B7.2d-5-10、B7.5d-5-10、B8.0d-5-10.前两者模型的破坏模式为钢筋拔出破坏,后两者为钢筋断裂破坏.钢筋拔出试件模型随着锚固长度的增加,钢筋与灌浆料之间的粘结强度增加,极限荷载增加明显,钢筋断裂试件模型的极限荷载变化较小.其中,模型B7.2d-5-10锚固长度为7.2d,极限荷载大于钢筋断裂试件模型,当锚固长度继续增加时破坏模式从钢筋拔出转为钢筋断裂,说明锚固长度的界限范围为7.2d至7.5d之间.对于套筒构造肋个数不同的模型A7.5d-5-10、B7.5d-5-10、C7.5d-5-10前两者均为钢筋断裂破坏,后者肋个数为6个,破坏模式为钢筋拔出.对于不同灌浆料厚度的模型B7.5d-5-8、B7.5d-5-10、B7.5d-5-12,破坏模式都为钢筋断裂.随着灌浆料厚度的增加,套筒对灌浆料以及灌浆料对钢筋的约束力降低,使得灌浆套筒接头整体的屈服强度和极限强度逐渐降低.对于不同套筒厚度的模型B7.5d-4-10、B7.5d-5-10、B7.5d-6-10破坏模式一致,屈服荷载和极限荷载相差不大.

3.3 设计模型的荷载-位移曲线

不同钢筋锚固长度、灌浆料厚度和构造肋个数灌浆套筒接头的荷载-位移曲线如图8所示.由图8(a)可知,加载初期全部接头曲线呈线性增长,达到屈服状态后进入强化阶段.接头B7.0d-5-10钢筋锚固长度较短,粘结强度较小,当接头承载力达到极限粘结强度时,接头发生粘结滑移破坏,钢筋拔出,曲线下降.接头B7.5d-5-10和B8.0d-5-10钢筋锚固长度较大,粘结强度较大达到极限荷载时接头发生钢筋断裂破坏,曲线下降.接头B7.2d-5-10的极限荷载高于锚固长度较大的两个接头,但破坏模式为钢筋粘结滑移拔出.说明此类接头的钢筋锚固长度界限在范围7.2d～7.5d之间.由图8(b)可知,屈服前荷载-位移曲线随灌浆料厚度的增大而减小,且屈服荷载和极限荷载也有一定程度减小,是由于灌浆料厚度增加套筒对灌浆料的约束减小且灌浆料对钢筋的约束减小所致.由图8(c)可知,接头A7.5d-5-10、B7.5d-5-10肋个数为4个和5个.破坏模式为钢筋断裂,曲线基本重合.接头C7.5d-5-10肋个数为6个,破坏模式为钢筋拔出破坏.说明套筒的变形段有一定界限,变形段长度对接头承载力有影响.当肋个数为4个和5个时变形段长度分别占套筒总长度的29%的36%,该比例承载力达到要求,套筒未发生断裂,表明该比例具有合理性.关于不同套筒厚度对接头的荷载-位移曲线影响较小.

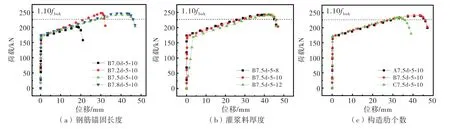
图8 不同参数对荷载-位移曲线的影响

3.4 应力分析

3.4.1 套筒应力分析

当接头达到极限荷载时对比不同构造参数套筒的应力分布.

图9为不同肋个数套筒应力对比,对于套筒光滑段内,光滑段中部应力较大.对于套筒整体,全部套筒都有明显的应力集中现象,应力集中于靠近套筒中部的第一条肋上,每条肋的应力从套筒中部到端部逐渐减小.其中4个肋(图9(a))和5个肋(图9(b))的套筒最大应力未超过屈服强度405 MPa,处于弹性阶段满足规范[13]要求,说明设计合理.6个肋(图9(c))的套筒的最大应力为409.8 MPa,超过屈服强度405 MPa(但处于微变形),理论上超过弹性变形段,且此类接头的破坏模式为钢筋拔出,实际工程中不宜使用.

图9 不同肋个数套筒应力

图10为不同壁厚套筒应力对比,3种壁厚套筒最大应力都未超过屈服应力405 MPa,处于弹性阶段,且满足性能要求,表明设计合理.套筒壁越厚套筒应力分布越不均匀,壁厚小的套筒最大应力值越大.4 mm 套筒(图10(a))应力分布较均匀,材料性能更能充分利用,实际工程应用中可减小造价.

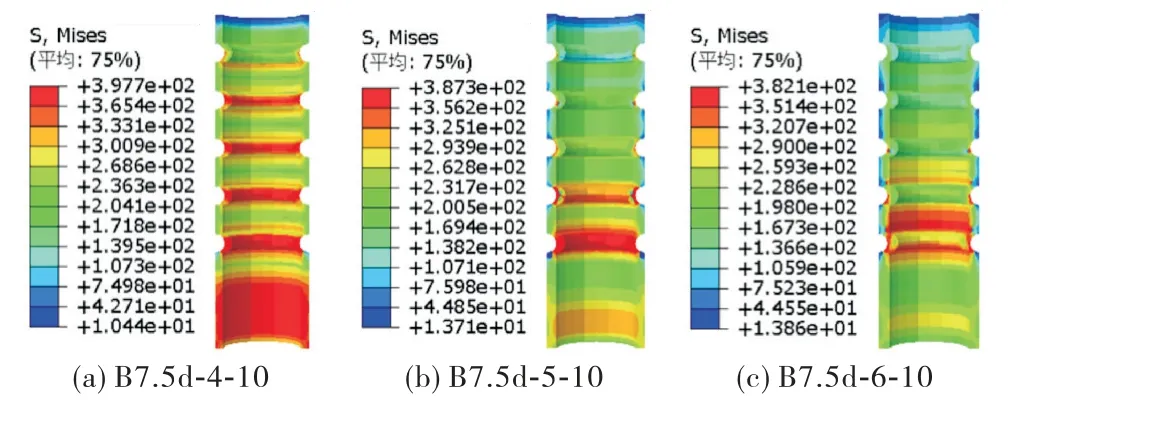
图10 不同壁厚套筒应力

模型在单向拉伸全过程中,取B7.5d-5-10模型观察套筒各肋应力变化规律,如图11(a)所示.可见靠近套筒中部的肋1的应力最大,从肋1到肋5,应力逐渐减小,与上述套筒应力分布结果一致.各肋从受力开始到接头达到屈服荷载时呈线性增长,且从肋5到肋1的斜率增加.接头达到屈服荷载之后套筒各肋的应力迅速增长,增长至接头达到极限荷载.说明弹性阶段接头承载力主要由钢筋承担,屈服后接头的承载能力由钢筋向套筒转移,但钢筋仍承受较大承载力.其中肋5的应力增长到一定程度开始下降,原因是由于接头达到一定承载力时靠端部的灌浆料压碎,套筒端部对灌浆料约束降低,则靠端部的肋5的应力降低.

此外对B7.5d-5-10模型施加压力作用观察各肋应力变化规律,如图11(b)所示.受压力作用时靠近端部的肋的应力比靠近中部的肋的应力大,应力增加速度快.肋1和肋5相差较大,肋2到肋4处相差较小.压力作用下较拉力作用下各肋的应力相对较小.

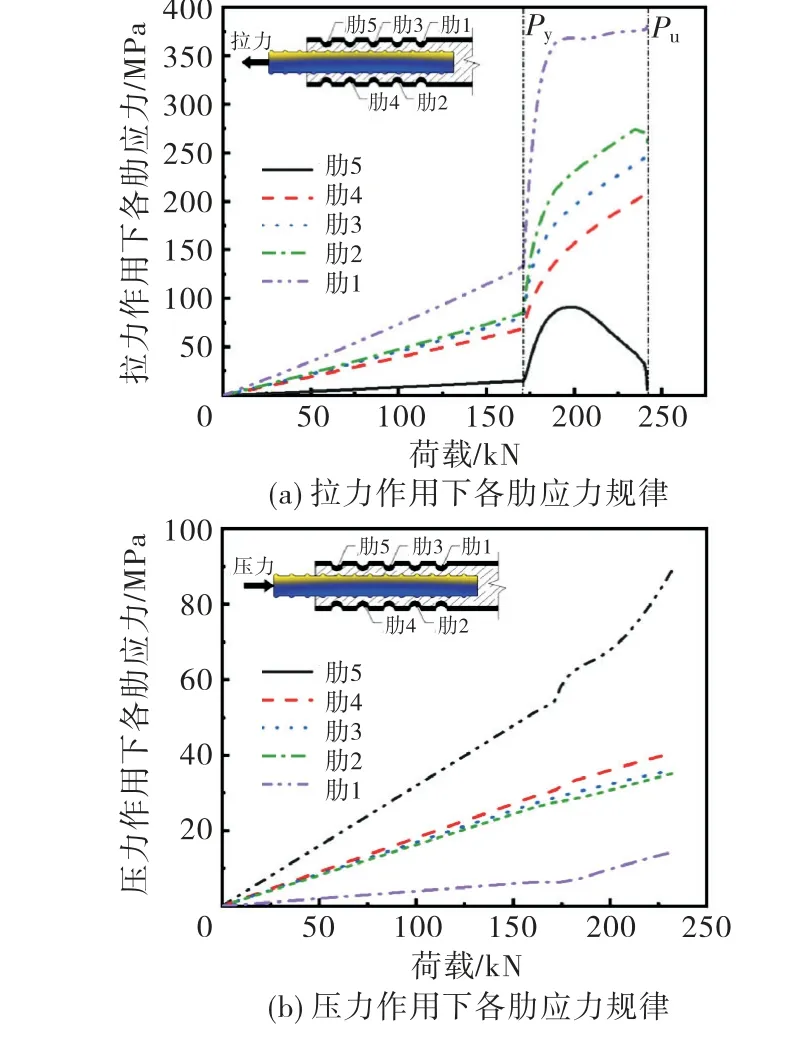
图11 接头拉力和压力作用下套筒应力的变化规律

3.4.2 钢筋应力分析

图12为B7.5d-5-10接头受到不同荷载时连接钢筋不同位置的轴向应力,横坐标为连接钢筋到套筒中部的距离,纵坐标为钢筋所受的轴向应力.相同荷载作用下钢筋从套筒中部到端部的轴向应力逐渐增大,且荷载越大时钢筋应力越大.随着荷载增大靠套筒中部与靠套筒端部钢筋轴向应力差值增大,即图中曲线斜率增大,则说明套筒接头所受荷载越大钢筋轴向应力分布越不均匀.

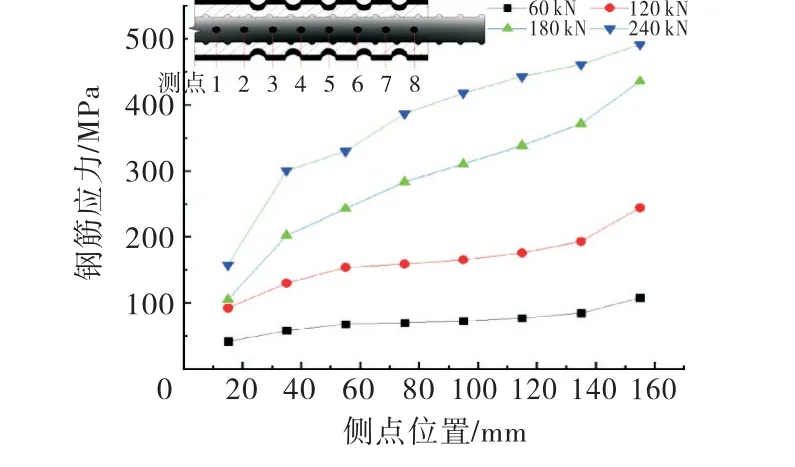
图12 钢筋的轴向应力

图13为B7.5d-5-10接头受到拉力为120 k N 时所对应钢筋的轴向应力分布,与图12结果一致.

图13 钢筋轴向应力分布

3.4.3 灌浆料应力分析

对比模型B7.5d-5-10(钢筋断裂)和B7.0d-5-10(钢筋拔出)极限荷载时灌浆料应力分布,如图14(a)和图14(b)所示.钢筋断裂试件模型较钢筋拔出试件模型的灌浆料应力大.钢筋断裂试件模型的粘结力较大,灌浆料的应力分布集中于套筒中部与钢筋粘结处.钢筋拔出试件模型达到极限荷载时粘结力失效发生粘结滑移破坏,钢筋和灌浆料之间还存在摩擦力作用,此时灌浆料应力分布较均匀.

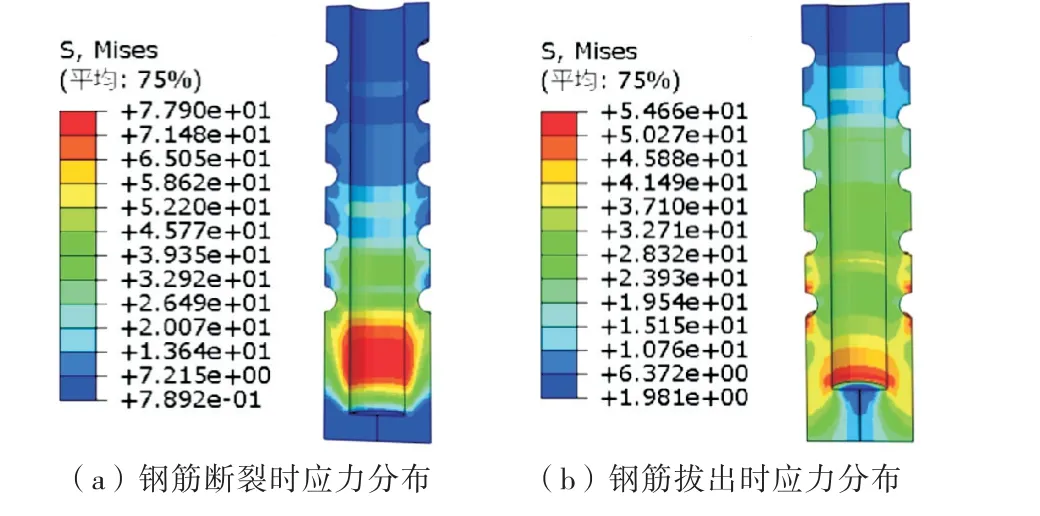
图14 灌浆料应力分布

4 结 论

1)本文采用2D 轴对称壳单元建模方式对新型灌浆套筒接头的单向拉伸试验进行了数值模拟验证,与试验结果较吻合.该方式建模简易,计算速度快,计算结果较准确,表明该建模方式合理可行.对于大型量多的轴对称结构可采用该建模方式进行数值模拟分析.

2)钢筋锚固长度(7.2～8.0)d时,fu/fbyk＞1.25且fu/fbuk≥1.10,满足规范[11]中I级接头和规范[12]中Type2类接头单向拉伸强度要求.

3)灌浆料厚度对接头承载力有影响.灌浆料厚度越大,套筒对灌浆料约束越小,灌浆料对钢筋约束越小,接头承载力降低.新型灌浆套筒的变形段长度不宜高于套筒总长度的36%.对于直径22 mm 钢筋的套筒厚度要求可低至4 mm,可充分发挥材料性能,减少材料使用,降低成本.

4)新型灌浆套筒接头在拉力作用下,套筒构造肋的受力从端部向中部增加,在压力作用下则相反.构造肋总体在拉力作用下较压力作用下受力大.套筒接头在拉力荷载作用下,连接钢筋的轴向应力从套筒中部到端部逐渐增加.