基于PCA-SVM 的边坡稳定性分析方法研究
姚 怡 王晓敏
(西安科技大学高新学院, 西安 710109)
21世纪以来,全球经济社会发展突飞猛进,随着越来越多工程活动的加剧,其地质条件也呈现出更加复杂化和多样化的特点[1,2],尤其在水电工程领域的表现更为明显.因此水利工程的边坡稳定性也备受关注,对于边坡稳定性的研究也随着水利工程活动的加速而不断深入[3,4].
早在20世纪初期,人们就已经开始了在边坡稳定性方面的经验和理论研究.20世纪中叶,类比法被大量应用于边坡失稳研究[5].六十年代,研究人员将结构面相关理论与边坡的失稳特征相联系,岩体结构的雏形就此产生[6].到了七十年代,研究方向开始向边坡的破坏过程和变形机理转变,累计性破坏理论和时效变形理论成为该阶段的研究热点[7].此后,由于计算机时代的来临,使传统的研究方法逐渐从定性研究向定量研究过渡[8].而通信技术的发展,为学科之间交叉和相互渗透提供了便捷.到20世纪末,我国西部大开发战略的提出和三峡工程的建设为边坡理论研究和实践应用提供了良好的平台[9,10],至此,系统科学开始在边坡稳定性研究中发挥作用.时至今日,多类研究方法已被应用于边坡稳定性研究,包括数值模拟[11]、界面元、快速Lagrange[12]、极限平衡[13]、离散单元[14]和神经网络[15]等.快速Lagrange和离散单元法的理论基本相似,均采用将镶嵌的岩体离散化后再进行分析[16],该方法可对不同的材料进行分析.当岩体切面发生形变时,可以对整个过程进行模拟,从而建立本构方程[17].该方法对数值模拟的分析过程较为繁杂,计算时间复杂度大,实际应用较为困难.神经网络作为现阶段较为常用的方法,它根据人脑的结构特征演化而来,具有良好的自我纠错能力、自学习能力和对环境的适应能力.神经网络将繁杂的各因子作为系统输入,建立非线性模型,利用模型对边坡稳定性进行分析[18].但这种方法具有收敛速度慢、容易陷入局部极小值的缺点.极限平衡法作为当下普遍用于工程实际的基本方法,能够定量地计算出边坡稳定性系数且计算简便[19].但该方法本身受理论假设和实际工程环境的限制,其计算准确率偏低[20].
以上研究中均忽视了边坡稳定性影响因子间的相互关系,而影响因子间的相互关系可能会使输入数据矩阵的结构变得复杂.主成分分析法作为解决此类问题的有力工具,在边坡稳定性研究中应用并不多见[21].同时,鉴于支持向量机在解决样本规模较小以及非线性问题中所表现出的优势,本文将二者相结合构建了PCA-SVM 模型用于边坡稳定性分析.
1 研究区概况
1.1 区域位置
崆峒水库位于甘肃省平凉市以西中山区、泾河上游峡谷内,泾河横穿大阴山,经源县至崆峒山,后向东部流淌.途径广袤的黄土塬,最终流向下游的平凉市.水库容量达2 970万m3,坝高达63.8 m,标准蓄水位1 523.2 m,堤坝前水头43 m,回水长度4.8 km.改扩建工程计划将容量提升1 602万m3,标准蓄水位提升14.6 m,堤坝前水头大约提升15 m,回水长度延长1.1 km[15].
1.2 地形地貌
水库地处平凉市崆峒区,位于崆峒山前峡出口,属峡谷型水库.泾河位于库区吊桥以上,流向由南至北且河道蜿蜒[22].谷底宽度为30~90 m,河床宽度为10~25 m,切割强烈,沿岸地势险峻,河谷大致呈V字状.崆峒山主峰位于水库西侧,坡险岸高且多为垂直陡崖.东侧地势略缓,坡度大约30°~50°.水库两岸坡体相对高差达400~500 m.
2 理论基础
2.1 PCA原理
PCA 是一种常用的主成分分析方法[23].实际问题中,各个输入变量之间存在某些相关性,这些相关性反映出变量之间存在一些重复信息.PCA 便是要寻求包含80%以上原变量信息的新变量,这些新变量可以由原变量线性表出,且相互之间不再具有相关性,所求得的新变量就是主成分,通常主成分包含的变量数为6个以内.
不妨设实际样本个数为n,每个样本均为p维随机变量,原始数据由下式矩阵表示:

实际上,因各变量因子所采用的单位和量纲不同,会造成数据不平衡的问题.因此,需要在主成分分析之前先对所有数据进行归一化处理.数据归一化的方法多样,本文采用如下较为常用的方式进行处理:

由式(2)对数据进行归一化处理后,得到新的变量X.其中,x i(i=1,2,…,p)表示原变量.用Y表示归一化处理后的新变量,则有:

新变量的对应分量分别称为原变量对应分量的第1,2,…,p个主成分.PCA 的本质是计算原变量X在主成分Y上的荷载c ij(i,j=1,2,…,p),它们分别属于相关矩阵的特征值的特征向量,特征值对应于该主成分的贡献,累计贡献率为:特征值λl,l=1,2,…,r,且r≤6就是对应的第l个主成分,累计贡献率通常为75%~85%以上.
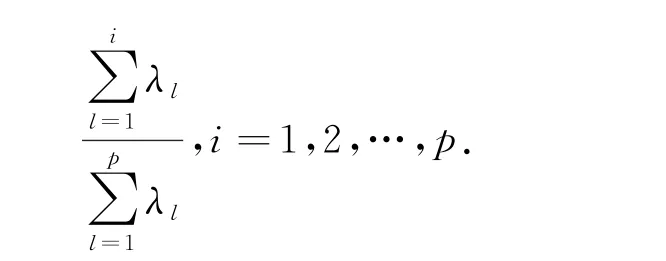
2.2 支持向量机SVM
支持向量机是结合统计学和结构风险最小原理的一种机器学习方法.该方法是基于小样本建立的综合了模型复杂性和学习能力的一种模型,属于有监督学习,在分类和回归分析中得到普遍应用.SVM 在解决分类和回归相关问题时本质上是一致的,只是二者输出数据的取值范围有所区别[18].
支持向量机将通过SVM 得到的回归问题的结论再应用到回归分析中.SVM 就是寻求使得与实际样本值y最大程度接近的拟合函数f(x).在该模型中,当且仅当y=f(x)时,才成立|y i-f(x)|=0.构建2ε的间隔(该间隔f(x)为中心),ε是损失边界,若该间隔内存在样本(|y i-f(x)|在承受范围内),则认为预测是准确的.SVM 的示意图如图1所示.

图1 SVM 示意图
数学模型由式(4)表示:


通过调整惩罚因子C可以降低算法的复杂度和提高准确率,从而式(4)转化为二次规划最优解的问题,该最优解可由Lagrange鞍点求得.将Lagrange函数对偶化,即可求得最小值

3 建立模型
根据之前的理论分析,基于PCA 和SVM 的边坡稳定性预测模型建立过程如图2所示.

图2 建模过程图
1)根据边坡外形、坡体结构、岩体力学性质以及外力等方面选取边坡稳定性影响因子集.
2)利用式2)对影响因子数据进行归一化处理.
3)对步骤1)中选取的影响因子进行PCA 分析并提取主成分.
4)将主成分划分为训练集、预测集和验证集,以主成分作为SVM 的输入,边坡稳定系数作为输出.
5)利用Grid-search对SVM 进行参数寻优,确定惩罚因子C和参数g.
6)通过预测集对经过训练的模型进行预测,并分析预测效果.
7)通过验证集对模型进行验证,并分析验证结果.
4 试验分析
支持向量机的数据处理速度取决于输入数据的大小,由于各输入数据之间存在一定的数据相关性,因此本文利用PCA 剔除掉不相关的主成分,使得SVM 模型的效果得到提高.
4.1 各影响因素相关性分析
根据已参阅的相关文献和整理的相关资料,在总结其他研究者经验的基础上,选取6个影响因素作为模型输入(详见表1).从文中所述研究区的水库工程中,随机选取1000 组历史边坡数据作为数据集.以976∶24的比例将该数据集划分为训练集和验证集.限于篇幅,表2 中仅列出了用于验证模型的样本数据,而模型训练用数据并未列出.

表1 边坡稳定性影响因素
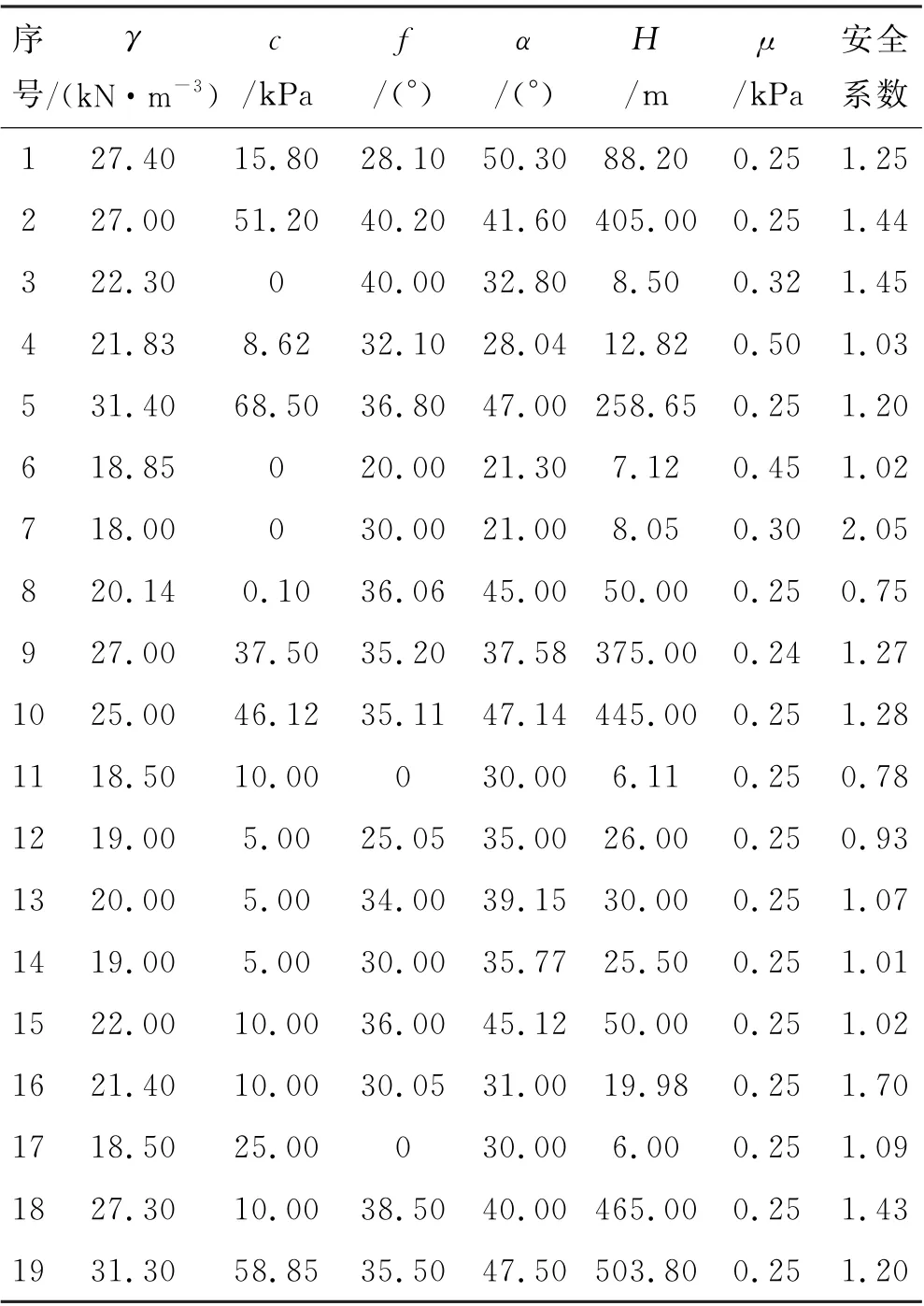
表2 边坡数据样本
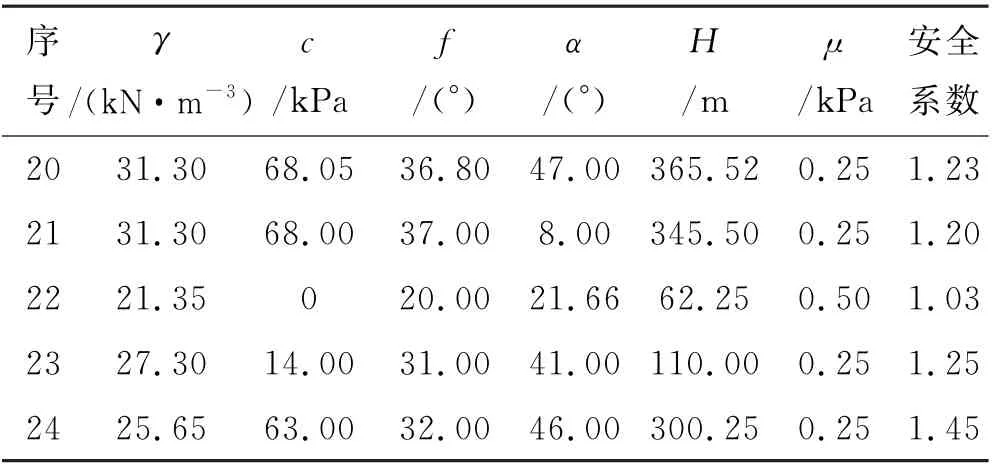
续表2 边坡数据样本
对表2中的数据进行相关性分析,各因素相关系数矩阵见表3.

表3 相关系数矩阵
从表3可以看出,本文选取的影响因素之间相关系数在0.8以上的有8个,这些影响因素之间具有某些相关性,SVM 输出的准确性必定会受到影响,所以有必要对输入数据的主成分进行分析.
4.2 主成分分析
通过计算,得到表2中输入数据的成分矩阵和方差,见表4和表5.

表4 成分矩阵
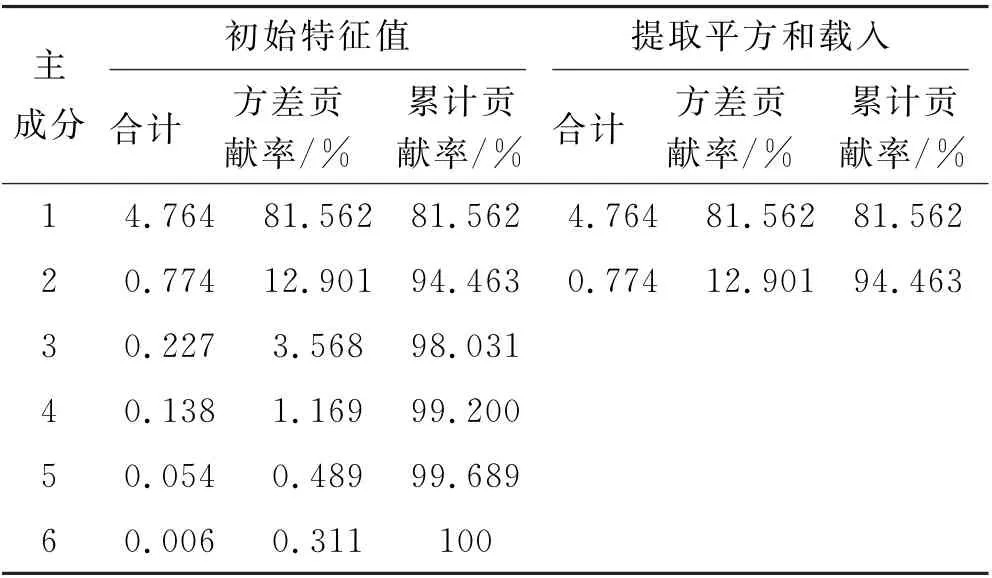
表5 解释的总方差
从表5 可以看出,主成分1 的方差贡献率为81.562%,满足主成分占总方差75%~85%的要求.主成分2的方差贡献率占总方差的12.901%,前两个主成分的方差贡献率已达到94.463%,能够有效的反映原变量的信息.
再将主成分矩阵中的数据通过SPSS 软件的Transform-computer变换,最终得到主成分载荷因子数据(见表6).

表6 主成分因子载荷矩阵
通过上表中的数据,得到主成分的表达式如下:

4.3 SVM 拟合效果
针对采用单一的支持向量机对边坡安全系数进行分析存在输入变量之间具有相关性且输入数据过多的不足,所以本文将主成分分析法与支持向量机相结合构建优选模型,对边坡安全系数进行合理的分析.
根据边坡模型的特点,选用RBF 核函数作为支持向量核函数,需要调整的参数为惩罚因子C和参数g.本节采用Matlab 进行模拟分析,使用Gridsearch参数寻优,最终确定惩罚因子C为1.625 1×104,核函数参数g为1.858 0×10-3.
从实际工程中随机选取976组数据用于模型训练,选取24组数据(见表2)用于模型验证,这里采用10折交叉法进行验证,以平均绝对误差[24]EMA和均方误差[25]EMS作为评价指标,结果见表7 和图3 所示.

表7 PCA-SVM 和SVM 的评价指标对比
从表7可以看出,无论从平均相对误差还是均方误差分析,使用PCA 的拟合效果明显比未使用PCA的拟合效果要好.从图3可以看出,相比单一的SVM模型,PCA-SVM 的拟合曲线更加接近于实际值.
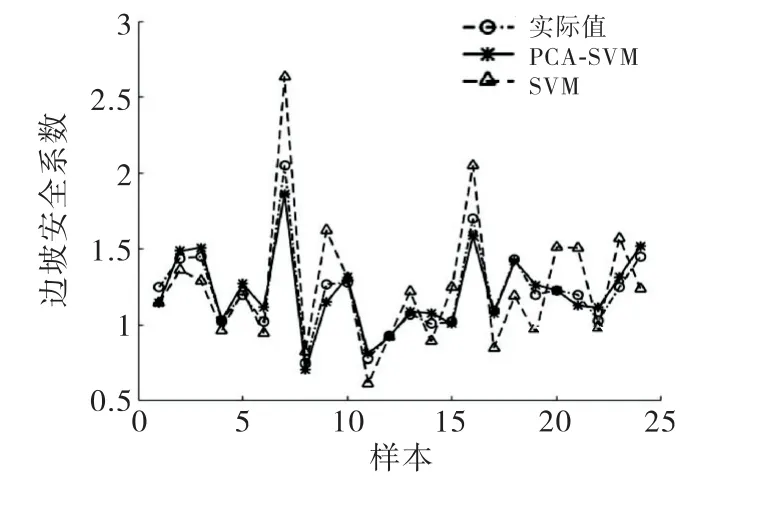
图3 数据拟合效果图
上面的实验已经表明PCA 的使用是有效的,为了验证PCA-SVM 的相比于其他模型的性能,再将本文模型与目前流行的遗传算法优化BP 神经网络(GA-BP)、梯度增强回归(GBR)、粒子群优化BP 神经网络(PSO-BP)和RBF 神经网络(RBF)的模型进行对比(所有模型均经过主成分分析),拟合结果如图4所示.
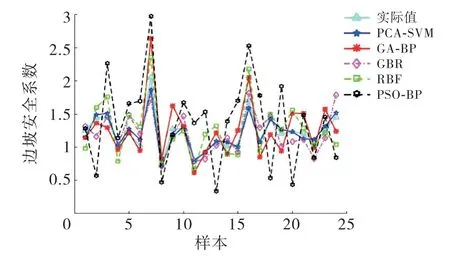
图4 5种模型拟合效果对比
同样,以平均绝对误差EMA和均方误差EMS作为评价指标对5种模型拟合结果的效果进行对比,结果见表8.
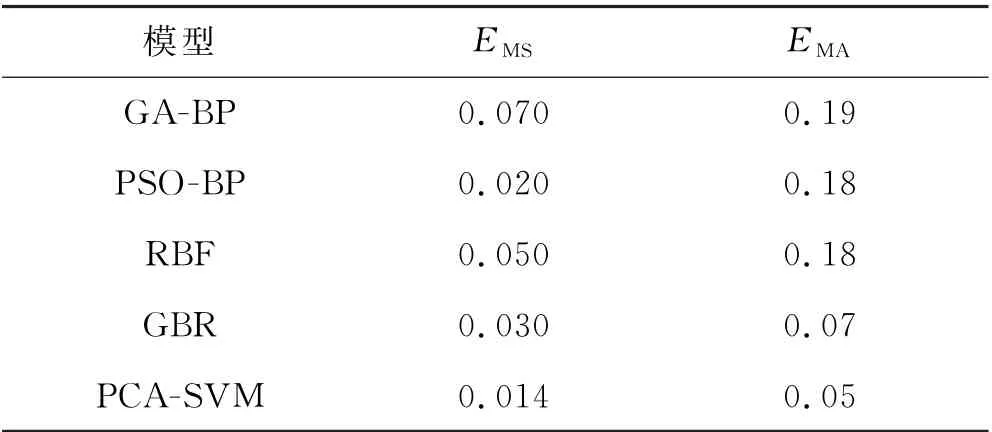
表8 5种模型的评价指标比较
5种模型的拟合曲线对比图中显示,本文提出的模型拟合效果与真实值最为接近,是所有模型中拟合效果最好的.表8的数据也显示出本文提出模型的误差是最小的,这说明在10次验证实验中,PCA-SVM模型的稳定性最高.
4.4 实例验证
本小节选取位于平凉市崆峒水库的A、B、C、D共4处边坡样本进行边坡安全系数预测,数据见表9.
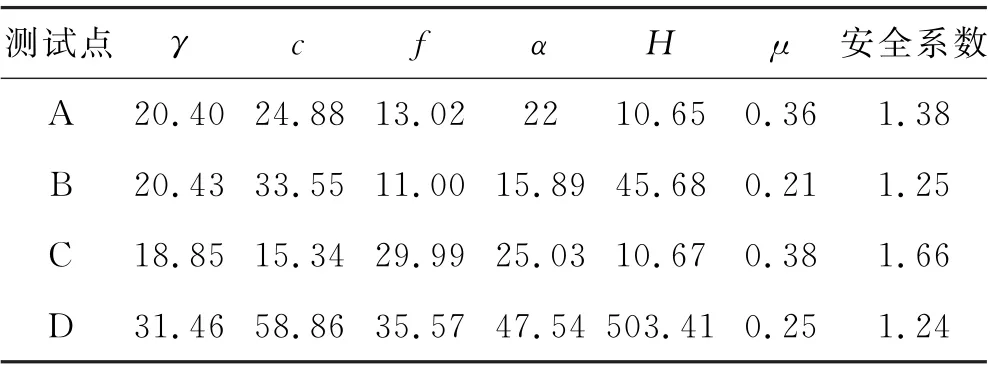
表9 预测样本
从图4和表8的结果可以看出RBF 和GBR 的拟合效果较好,,故利用GBR、RBF 和PCA-SVM 对以上数据进行验证,结果见表10.
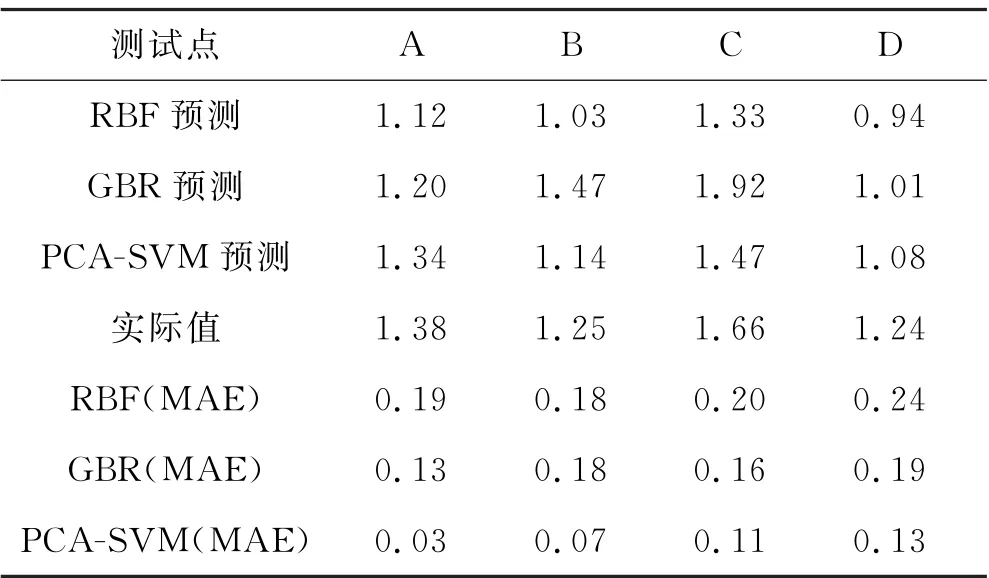
表10 预测结果比较
从表10可以看出,PCA-SVM 模型对于4处预测点预测结果的绝对误差分别为0.03、0.07、0.11和0.13,和其它两种模型相比均为最小,预测值与实际值也更接近.再次表明了PCA-SVM 模型在边坡安全系数预测方面的有效性.
5 结 论
1)本文采用主成分分析和网格搜索支持向量机相结合的方法,对边坡稳定性进行了分析.利用PCA实现了对输入数据的降维处理,避免了因输入变量间的相关性造成的计算复杂化,过程简洁明了,实验表明结果准确,该方法是有效的.
2)PCA-SVM 模型与单一SVM 模型的预测结果表明,经PCA 处理后的预测准确率更高,平均绝对误差和均方误差也明显减小.验证样本集的平均绝对误差EMA从0.23降至0.047,均方误差EMS从0.19降至0.014,表明将PCA 与SVM 相结合应用于边坡稳定性分析是有效的.
3)本文提出的PCA-SVM 模型与常用的遗传算法优化BP 神经网络(GA-BP)、梯度增强回归(GBR)、粒子群优化BP 神经网络(PSO-BP)和RBF神经网络(RBF)的模型进行对比,结果表明PCASVM 模型的拟合结果与实际值最匹配,同时平均绝对误差和均方误差也最小.研究区的测试结果再次验证了PCA-SVM 模型的有效性和可行性.本文所采用的研究方法为边坡稳定性研究领域提供了一种新的思路.
4)因本研究所使用的数据集样本类型和数量有限,实验结果不可避免的具有一定局限性,后期还需要更多工程数据以提高模型的普适性和泛化性.

