玄武岩纤维混凝土组合梁抗弯性能试验研究

王 仪, 张志文, 葛文杰, 严卫华, 陆伟刚

(扬州大学a. 建筑科学与工程学院, 江苏 扬州 225127; b. 水利科学与工程学院, 江苏 扬州 225009)

传统的钢筋混凝土目前仍是建筑工程中的主要结构材料, 但由于受温度、湿度变化和酸碱腐蚀等影响,混凝土结构容易产生钢筋锈蚀、混凝土劣化、强度降低、疲劳损伤等病害．将适量的纤维增强复合材料(fiber reinforced polymer, FRP)均匀掺入混凝土中形成纤维混凝土是改善此类问题的常用方法[1]．常用的FRP掺料种类主要有钢纤维、碳纤维、聚丙烯纤维、玻璃钢纤维、玄武岩纤维以及天然植物纤维等．其中, 玄武岩纤维增强混凝土(basalt fiber reinforced concrete, BFRC)是一种优良的高性能混凝土材料, 可以弥补普通混凝土材料抗拉强度低、韧性差及裂缝宽度难以控制等缺点．Zhang等[2]通过受弯试验发现BFRC梁较普通混凝土梁的刚度及抗裂荷载有显著提高; 赵燕茹等[3]通过四点受弯试验分析了BFRC梁的破坏模式并讨论了不同纤维体积率的影响, 发现BFRC梁的开裂荷载和极限荷载均大于普通钢筋混凝土梁, 且挠度、延性和韧性均有所增强; Branston等[4]通过试验评估了短切纤维在抑制钢筋混凝土梁早期开裂方面的作用, 发现首次开裂强度随玄武岩纤维掺量的增加而增加; Haido[5]在试验基础上提出BFRC弹塑性本构模型并在有限元模型中进行计算,验证了该模型的正确性; 敖士楷[6]在过镇海等[7]提出的混凝土轴心受压和受拉的应力-应变全曲线基础上, 对不同强度及纤维掺量的BFRC混凝土试件进行受压试验, 拟合得出BFRC全曲线模型; 王艳苓[8]通过试验对BFRC劈裂抗拉强度线性拟合得到BFRC劈裂抗拉强度与轴心抗拉强度之间的关系; Alnahhal等[9]将再生骨料和BFRC结合并进行抗弯试验, 发现添加短切玄武岩纤维后梁体抗弯承载力较普通钢筋混凝土有显著提高; Chen等[10]通过抗剪试验发现, 随着纤维体积率的增大, BFRC梁体开裂荷载明显增大, 斜裂缝宽度显著减少; Abed等[11]在混凝土梁中添加不同类型纤维并对比研究其抗弯性能, 发现玄武岩纤维增强复合材料能显著提高梁的曲率及延性．

以上研究均是对于BFRC构件与钢筋混凝土构件的对比研究, 鲜有针对BFRC与混凝土组合构件复合截面的研究．本文拟采用BFRC作为混凝土复合梁底部受拉区域,通过对不同BFRC高度组合梁进行四点弯曲试验,研究不同高度比例的BFRC对组合梁的弯矩-挠度曲线、弯矩-钢筋应变曲线、混凝土界面平均应变、弯矩-曲率曲线、裂缝发展、延性系数等抗弯承载性能的影响．拟通过MATLAB软件建立弯矩-曲率模型, 并基于平截面假定和相关规范提出极限荷载简化计算方法,为实际工程提供参考．

1 试验内容

1.1 试件设计

图1为试件正截面示意图．试件尺寸均为长3 100 mm, 宽200 mm, 高300 mm．上部架立筋均为2Φ10, 箍筋为Φ8@200, 受拉钢筋为3Φ12的HRB400钢筋, 保护层厚度为35 mm．L1、L2、L3三种组合梁的BFRC高度分别为0, 100, 150 mm, 纯弯段为600 mm．

图1 试件截面示意图(mm)Fig.1 Section diagram of specimen

1.2 试验材料

试验所用的水泥为P.O 42.5级普通硅酸盐水泥; 细骨料为普通河沙、中砂, 粗骨料为粒径为5～20 mm的碎石; 短切玄武岩纤维长15 mm, 直径10 μm, 密度为2 650 kg·m-3, 伸长率为3.1%, 拉伸强度为4 100 MPa, 弹性模量为100 GPa; 聚羧酸高效减水剂, 减水率40%．由质量比计算得到的玄武岩纤维混凝土的水灰比为0.37, 水、水泥、沙、石的配合比为1∶2.7∶3.88∶6.0, 纤维体积率0.1%．BFRC轴心抗压强度为31.05 MPa, 劈裂抗拉强度为2.82 MPa; 混凝土轴心抗压强度为25.1 MPa．

1.3 试件制作及加载

在浇筑试件前, 将底部跨中位置的钢筋对称打磨光滑, 用酒精棉对打磨处进行擦拭, 再用AB胶包裹的应变片粘贴在对应位置上, 防止试验过程中应变片破坏; 将钢筋放置于模具内,对L1梁直接浇筑混凝土; 对L2、L3梁采用分层浇筑法, 分别先浇筑100 mm、150 mm高的BFRC混凝土,再浇筑普通混凝土．浇筑后对试件振捣密实, 减少浇筑时产生的空隙．然后找平梁表面, 覆盖防水布,于24 h后进行拆模并盖布保护, 定期洒水养护．

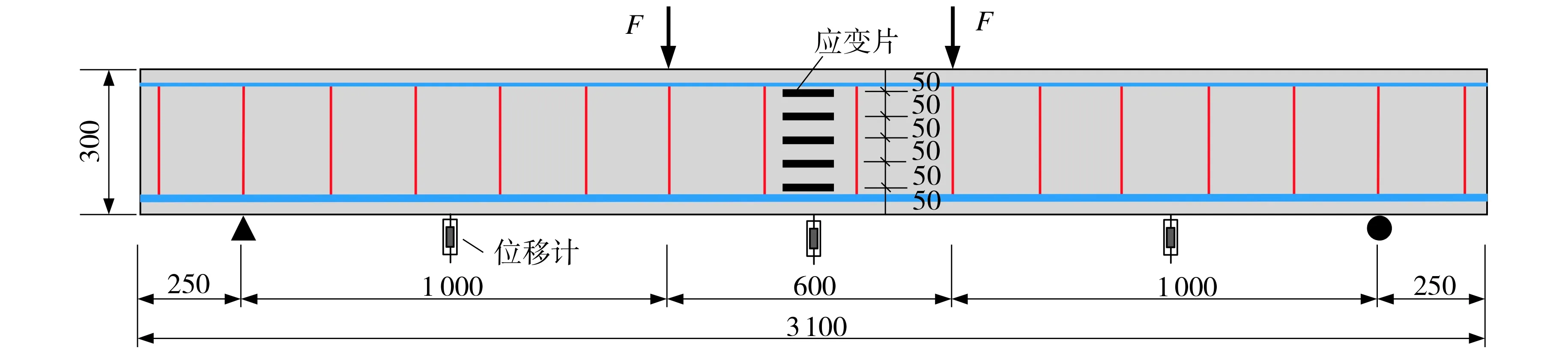
图2 四点受弯试验示意图(mm)Fig.2 Diagram of four point bending test

图3 试验装置Fig.3 Test setup

图2为四点受弯试验示意图．在梁底部跨中、加载点和支座位置布置位移传感器; 在下部钢筋纯弯段每间隔150 mm布置应变片, 箍筋处每间隔75 mm布置应变片; 在梁竖直面上每间隔50 mm布置应变片,通过换算得出试件截面不同高度的平均应变．图3为试验装置图．通过油压千斤顶对试件进行预加载,检测各仪器正常后开始试验, 通过荷载传感器测量并利用TDS-530数据采集器记录．先以计算开裂荷载的10%进行逐级加载, 临近开裂荷载时再以1 kN为增幅逐级加载, 直至开裂; 开裂后按照屈服荷载的10%逐级加载, 临近屈服荷载时再以1 kN为增幅逐级加载,直至屈服; 钢筋屈服后, 以控制每级1 mm位移逐级加载直至结束．每级加载后维持10 min等待仪器读数稳定, 测量并记录数据, 并用记号笔于试件上勾勒出每级荷载作用下的裂缝分布情况．

2 试验结果

2.1 破坏形态

图4为各试件的裂缝分布图．随着荷载逐渐增加, L1在纯弯段梁下部受拉区出现竖向裂缝, 荷载达到钢筋屈服后,裂缝迅速扩展且梁挠度增幅逐渐增大;荷载持续增加,上部混凝土开始碎裂,发生适筋破坏．随着荷载增大, L2梁纯弯段的底部出现少量竖向裂缝,但裂缝分布比L1稀疏; 裂缝发展至组合截面处后,裂缝宽度显著增大,裂缝开始逐渐产生较多分支,说明BFRC可以缓解裂缝的伸展,玄武岩纤维的桥接作用明显,相较于普通混凝土可以有效抑制裂缝的产生及发展．同L2相比,L3初始阶段裂缝扩展更缓慢,BFRC处的裂缝较少,而普通混凝土处的裂缝发展则较为迅速．L2、L3组合梁在受弯过程中,BFRC与混凝土交界处均未发现分层现象,说明BFRC与混凝土组合界面粘结良好, 具有较好的协同工作能力．

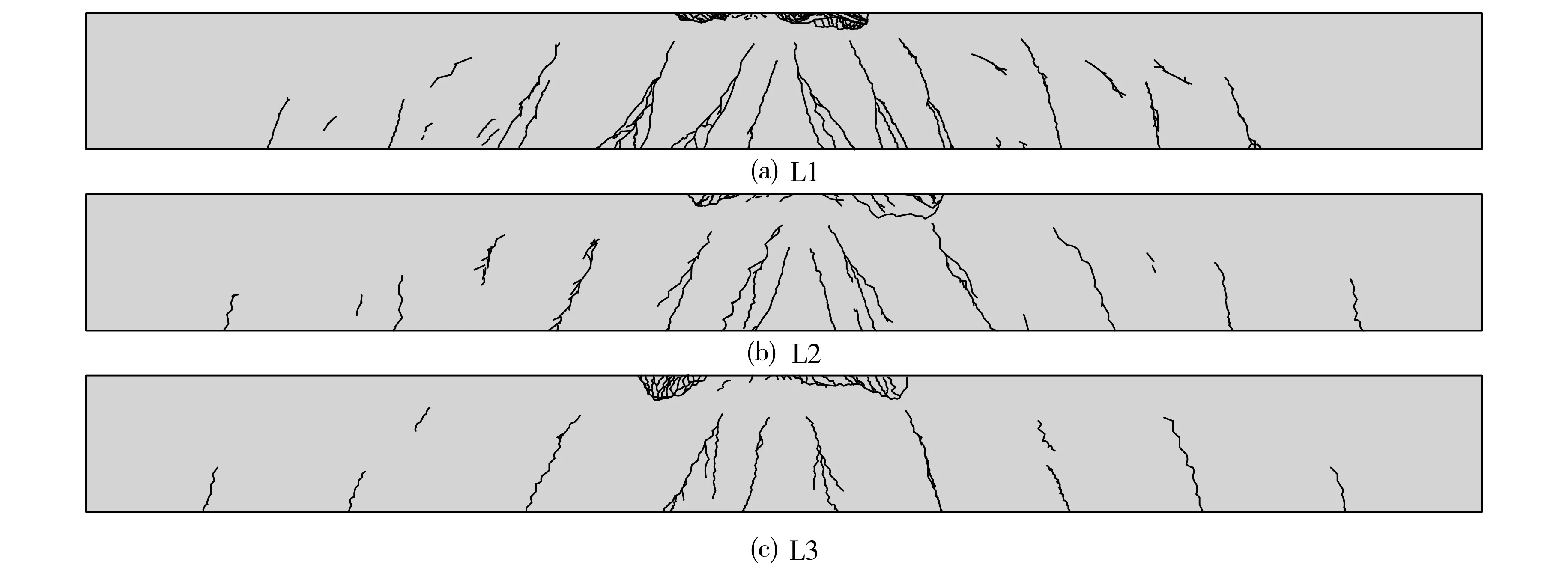
图4 裂缝分布Fig.4 Cracks distribution

2.2 弯矩-挠度曲线

图5 弯矩-挠度曲线Fig.5 Moment-deflection curve

图5为试件弯矩-挠度曲线．在试件逐级加载过程中, 试件跨中位置出现第一条或第一批裂缝时,视为试件开裂;当钢筋达到屈服应变或弯矩-挠度曲线出现明显转折时, 视为试件屈服; 当上部混凝土压碎破坏时,停止加载,构件破坏．图5中的曲线可分为: 1) 弹性阶段, 此时加载荷载较小,梁截面尚未产生开裂, 混凝土、BFRC处于弹性阶段,钢筋应变较小, 弯矩-挠度曲线近似为线性增长; 2) 弹塑性阶段, 试件开裂后随着荷载的继续增加, 梁下部跨中位置开始出现裂缝, 此时弯矩-挠度曲线出现拐点,之后挠度逐渐增大,裂缝由跨中向两端延伸,并逐渐向上蔓延; 3) 塑性阶段, 弯矩-挠度曲线达到第二个拐点, 钢筋逐渐达到屈服, 此时挠度增加速率变大,较小荷载即可引起较大挠度,直至试件破坏．卸载后, 试件存在回弹现象,体现出塑性特征．由图5可知,随着BFRC高度的增加,试件开裂荷载、屈服荷载、极限荷载均显著提高,当试件达到开裂荷载及屈服荷载时, 对应的挠度均显著减小．相同荷载情况下, L1、L2、L3对应的挠度逐级减小,说明随着BFRC高度增加,抑制挠度发展的能力增强; 试件破坏前,L2、L3同L1相比,具有较强控制变形的能力,且L3更强．

2.3 弯矩-钢筋应变曲线

图6为试件弯矩-钢筋应变曲线．如图6所示, 弯矩-钢筋应变曲线与弯矩-挠度曲线在弹性阶段变形均较小; 当进入屈服阶段时,受拉钢筋与箍筋变形速率显著增大．弯矩-钢筋应变曲线和弯矩-挠度曲线过程大致相同, 说明钢筋与BFRC、混凝土粘结良好, 达到协同变形效果．相同荷载时BFRC高度越高, 箍筋应变越小, 说明BFRC有效减小了箍筋变形,提高梁整体刚度及抗弯承载力．

图6 弯矩-钢筋应变曲线Fig.6 Moment-steel strain curve

2.4 组合截面平均应变沿高度分布曲线

图7为试件跨中在不同正截面极限弯矩Mu条件下沿梁截面高度的平均应变．根据加载过程中不同混凝土梁高度的应变片读数, 计算得到试件50、100、150、200、250 mm高度的平均应变．由图7可知, 纯弯段混凝土各点的应变与该点到中性轴的距离近似成正比关系, 说明各试验梁在受弯过程中均符合平截面假定,且混凝土与BFRC的整体协同性能良好．随荷载逐渐增大,混凝土梁L1的中和轴高度上升较为明显,复合梁L2和L3上升缓慢．L2、L3下部BFRC受拉应变明显小于L1下部普通混凝土,且随着BFRC高度增加,L3下部BFRC受拉应变小于L2,说明玄武岩纤维具有良好的桥接作用．

图7 试件截面平均应变沿高度分布曲线Fig.7 Average strain distribution curve along height of cross-section

3 BFRC组合梁抗弯承载力分析

3.1 弯矩-曲率关系

图8 弯矩-曲率曲线流程图Fig.8 Flow chart of moment-curvature curve

基于平截面假定, 利用材料本构, 通过MATLAB软件对组合梁进行正截面受力分析, 并采用积分法计算试件的弯矩-曲率(M-φ)关系．图8为积分法编程计算弯矩-曲率关系的流程图．

首先, 设定受压区高度为xj,j=1,2,…,200, 且x0=0,x1=h0,…,xj+1=(xj-1+xj)/2, 其中h0为截面有效高度; 设定混凝土受压区压应变εc,i以0为初值、按步长εcu/i(i=1,2,…,1 000)增加到极限压应变εcu．其次, 对混凝土受压区高度进行i等分得到其分层厚度xj/i; 对混凝土受拉区高度进行i等分得到受拉区分层厚度(h-xj)/i, 其中h为混凝土梁截面总高度．然后, 根据应变协调关系, 得到受压钢筋压应变ε′s=εc,i(xj-as)/xj, 其中as为受压钢筋保护层厚度; 受拉钢筋拉应变εs=εc,i(h0-xj)/xj; 混凝土第k层压应变εc,k=(k-0.5)εc,i/i;混凝土第k层拉应变εt,k=(k-0.5)[(h-xj)/i]εc,i/xj．将各部分应变代入材料本构中, 求解各部分应力并判断受力平衡, 然后输出各部分应力．最后, 将得出的应力对中性轴求矩, 计算总弯矩值M并输出曲率φ, 当j>200时终止迭代．

钢筋本构采用弹塑性模型．普通混凝土及BFRC受压、拉本构曲线参考文献[6], 轴心抗拉强度利用劈裂抗拉强度换算[8]．混凝土受压本构模型为

其中σc和εc为混凝土的压应力和压应变;fc为混凝土设计抗压强度; 混凝土达到设计抗压强度时的压应变εc0=0.002+0.5(fcu,k-50)×10-5,fcu,k为立方体混凝土抗压强度; 混凝土的极限压应变εcu=0.003 3-(fcu,k-50)×10-5;a及α为多元非线性回归分析拟合得到的关于不同强度下受压应力-应变曲线的下降段影响系数[6], 对于普通混凝土取值分别为1.4和2.0, 对于BFRC取值分别为1.4和2.3．

混凝土受拉本构模型如下所示,

其中σt和εt为混凝土的拉应力和拉应变,ft为混凝土设计抗拉强度,εt0和εtu为混凝土达到设计抗拉强度时的拉应变和混凝土的极限拉应变, 玄武岩纤维影响系数αf=0.312ft/(1+3.58λf), BFRC纤维含量特征值λf=ρflf/df, 式中ρf为纤维体积率,lf和df为玄武岩纤维长度和直径.

图9 弯矩-曲率曲线Fig.9 Moment-curvature curve

图9为采用积分法计算得到的试件弯矩-曲率关系．由图9可知, 随着BFRC高度的增加, 抗弯承载力明显增强．图9显示了受弯试件由开裂到屈服再到破坏的发展过程．当试件发生开裂时, 试件抗弯刚度突然下降, 继续加载后, 试件承载力又逐渐上升, 整体趋势与弯矩-挠度曲线相似, 说明积分法编程计算的弯矩-曲率关系与试验结果相符．

3.2 截面曲率延性分析

表1为试件屈服曲率、极限曲率及截面曲率延性系数．由表1可见, 利用BFRC增强底部受拉区抗拉强度对试件屈服曲率和极限曲率的影响不明显, 说明BFRC高度对组合梁的截面延性影响不大．由于延性的影响因素主要为纵向钢筋配筋率、混凝土极限压应变、钢筋屈服强度及受压混凝土强度等,当下部BFRC高度小于中和轴高度时,受压区高度内全为普通混凝土,故BFRC高度对试件延性无影响;当BFRC高度大于中和轴高度,上部受压区为普通混凝土与BFRC协同作用,由于BFRC较普通混凝土的抗压强度提升不明显,延性提升也较小,所以几乎对试件延性无影响．通过计算,L1、L2、L3的曲率延性系数均为4.58,与试验值对比误差极小,验证了理论的可靠性．

表1 屈服曲率、极限曲率及曲率延性系数Tab.1 Yield curvature, ultimate curvature and ductility coefficients of the curvature

3.3 极限荷载简化计算

图10为理想配筋条件下BFRC组合梁简化极限荷载应力-应变分布．其中hs为保护层厚度,he为BFRC高度,ht为BFRC底部到中和轴的距离,εsy为钢筋的屈服应变,εft为BFRC底部受拉应变,εc为上部混凝土压应变,σc为上部混凝土压应力,σft为下部BFRC拉应力．参考《纤维混凝土结构技术规程》CECS 38—2004, 由于上部钢筋起架立筋作用, 故不作考虑．根据图10中组合梁正截面应变协调关系, 建立力的平衡方程αcfcbx=fyAs+fftbhe, 其中受压区等效矩形高度x=xcβc,xc为截面最大承载力时混凝土受压区压应变高度, 根据《混凝土结构设计规范》 GB 50010—2010, 取αc=1.0,

表2 极限荷载试验值与计算预测值对比Tab.2 Comparison of ultimate load test value and predicted value

βc=0.8; 当xc≤(h-he)时,Mu=fyAs(h0-x/2)+fftbhe(h-he/2-x/2); 当xc> (h-he)时,Mu=fyAs(h0-x/2)+fftb(h-x/βc)(h-he/2-x/2)．

表2为极限荷载试验与计算预测对比,由表2可知, 随着BFRC高度的增加,荷载随之提高,组合梁简化极限荷载理论计算结果与试验值平均误差较小,说明该理论可精确预测适筋破坏条件下组合梁极限荷载．

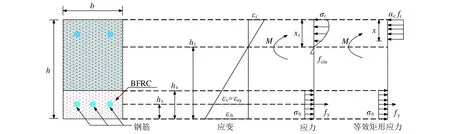
图10 正截面应力-应变分布图Fig.10 Stress-strain distribution of normal cross-section

4 结论

通过对玄武岩纤维混凝土组合梁受弯性能试验及数值模拟的研究,得到如下结论:

1) BFRC组合梁截面符合平截面假定; BFRC、混凝土与钢筋变形协调,协同工作能力良好,由于玄武岩纤维良好的桥接作用,能够有效抑制裂缝的开裂及伸展,显著提高下部受拉区抗拉强度,以此提高梁受弯承载能力,且BFRC高度比例越高,抗弯承载力提高越显著,挠度降低得越明显．

2) BFRC高度的提升对组合梁试件延性几乎无影响．

3) 组合梁极限荷载简化计算公式,合理考虑了BFRC组合梁高度影响,对其受拉和受压区域进行划分计算,结果与试验相吻合,平均误差较小,可为设计施工单位在BFRC组合梁的计算和设计方面提供理论参考依据．