基于功率键合图的低速重载馈能减震器动态特性分析

沈 辉, 周竹馨, 关 栋, 2, 3*, 李 竞, 张 纯

(1. 扬州大学机械工程学院, 江苏 扬州 225127; 2. 常柴股份有限公司, 江苏 常州 213000;3. 江苏奔宇车身制造有限公司, 江苏 扬州 225212)

传统液压减震器将地面激励、转弯侧倾等工况消耗的汽车驱动能量以摩擦或热能等方式耗散至空气中, 仅有12%～30%的燃料能量用于克服道路摩擦和空气阻力, 其主要损失为减震器中的振动耗散,导致高速阻尼失效和油液泄漏,从而增加碳排量,加剧能源危机与环境污染[1-2]．近年来, 新能源汽车及汽车节能技术成为研究热点[3], 但电动汽车的发展仍受制于续驶里程短、电池成本高等问题[4]; 因此, 国内外学者针对新能源车辆开展了大量的能量回收研究．Azam等[5]设计了一种齿条齿轮式机械能量回收器, 收集车辆与减速带碰撞期间以振动形式耗散的动能, 在12 mm·s-1的激励速度和150 N的作用力下, 可获得11.99 W的峰值输出功率和20.57 V的峰值电压; 张晗等[6]提出一种液电式馈能半主动悬架系统方案, 其簧载质量加速度、悬架动行程、车轮动位移的综合性能介于被动悬架和传统半主动悬架之间,能量回收效率为12.86%; Li等[7]设计了复合悬架模式,实时切换控制策略和能实现能量双向流动的可变电压源系统,仿真分析得出复合悬架动挠度均方根值降低19.83%,消耗的能量减少了30.7%,复合悬架在有效改善悬架动态性能的同时可实现振动能量回收．此外,关于车联网和智能驾驶的馈能式传感器供电研究也取得了一些成果[8-11]．上述研究虽能有效回收悬架等系统的振动能量,但其阻尼力小、回收功率低,仅适用于电动轿车等小型车辆．针对低速重载工况下的重型货车或工程机械特种车辆,本文拟设计一种基于滚珠丝杠副的馈能减震器,并研究其动态特性与能量回收效率,分析阻尼特性与馈能效率的影响因素,以期为低速重载馈能减震器的优化设计提供理论基础．

1 滚珠丝杠副馈能减震器的基本结构

图1为馈能悬架系统示意图．由图1可知, 滚珠丝杠副馈能减震器主要由轴承、滚珠丝杠、滚珠丝杠螺母、锥齿轮、联轴器、齿轮箱和发电机等组成．其中滚珠丝杠两端与底座相连,当螺母上下运动时,带动滚珠丝杠旋转;锥齿轮改变滚珠丝杠旋转运动的传动方向,使结构更加紧凑,并将动力传递到发电机输入轴; 齿轮箱用于提高转速,直流电机用作发电机．齿轮箱传动比的选择对整体性能至关重要, 传动比较高时,系统可获得较高的阻尼系数, 但传动效率较低[12]; 因此, 齿轮箱传动比的选择应折中考虑性能和传动效率．本文选取的传动比为44, 齿轮传递参数如表1所示．

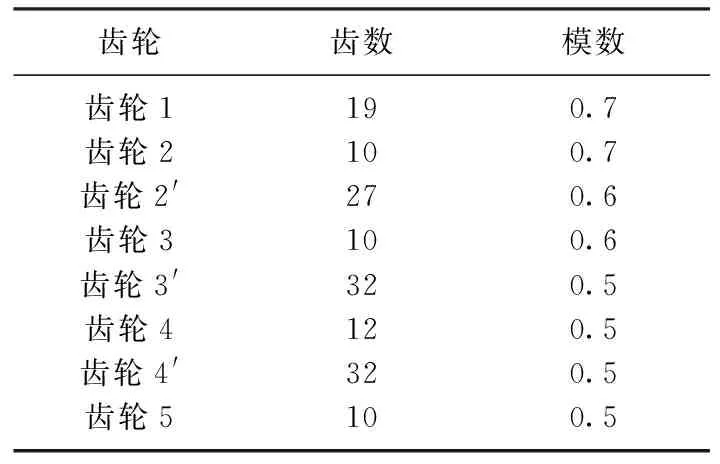
表1 齿轮传递参数Tab.1 Transmission parameters of gears

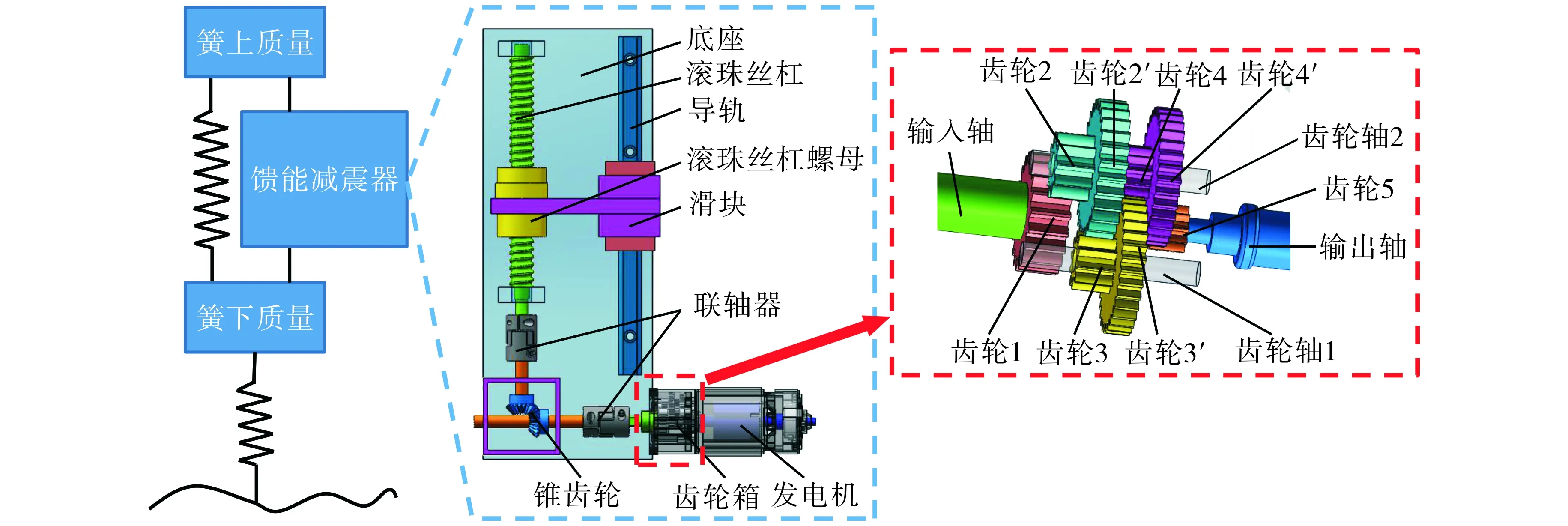
图1 馈能悬架系统示意图Fig.1 Schematic diagram of regenerative suspension system

2 基于功率键合图理论的能量模型

2.1 功率键合图模型

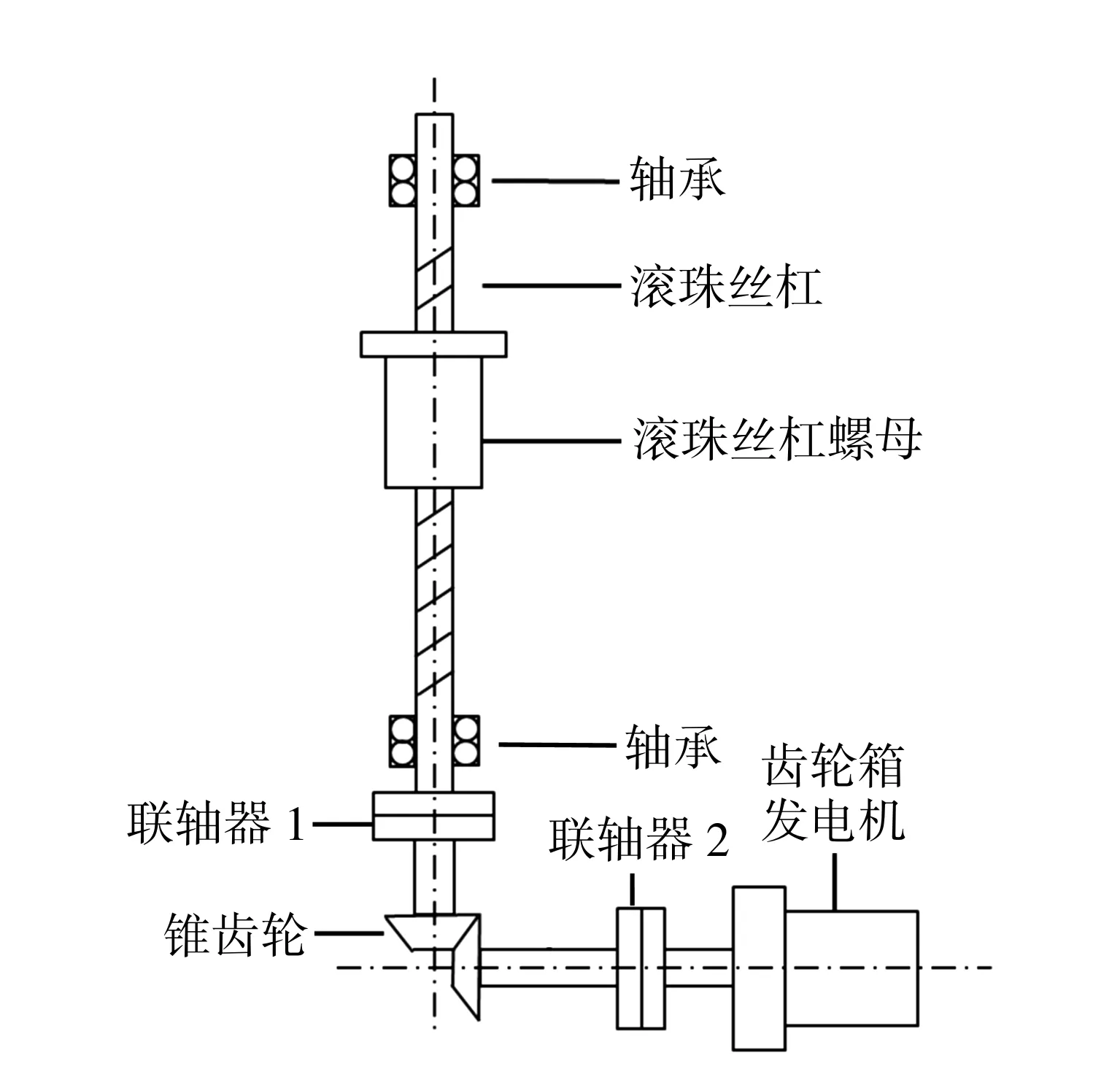
图2 滚珠丝杠副馈能减震器物理模型Fig.2 Physical model of ball screw energy-harvesting shock absorber

功率键合图理论基于工程系统中的功率移动、转换、存储和耗散原理[13], 分析滚珠丝杠副馈能减震器的实际结构,提取关键构造,得到简化物理模型,如图2所示．

通常只有部件的刚度、阻尼和惯性/质量被认为与功率键合图中的容性元件、阻性元件和惯性元件相匹配[14], 因此, 在滚珠丝杠副馈能减震器的物理模型转换为相应的功率键合图模型之前,应根据功率键合图的建模特点处理关键部件的力学特性．具体处理如下:

1) 作用在滚珠丝杠螺母上的驱动力为动力源;

2) 综合研究锥齿轮、联轴器和轴承结构, 假设三者均受到轴向和扭转作用,其扭转阻尼和扭转刚度作用于同一中心点[14];

3) 滚珠丝杠螺母副作为变换器, 将平移运动转换为旋转运动, 工作过程应考虑轴向和扭转刚度以及阻尼效应;

4) 对负载进行集中质量处理,考虑负载的拉压刚度和阻尼．

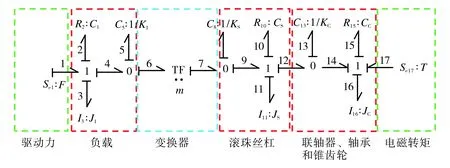
图3 滚珠丝杠副馈能减震器的功率键合图模型Fig.3 Power bond graph model of ball screw energy-harvesting shock absorber

以滚珠丝杠螺母副为边界,系统分为平移部分和旋转部分,其中平移部分包括滚珠丝杠螺母和负载, 旋转部分包括滚珠丝杠、锥齿轮、联轴器和轴承．建立滚珠丝杠副馈能减震器的功率键合图模型, 如图3所示．其中,TF为变换器,F和T为键上的势变量;Kl和Ks分别为负载和滚珠丝杠的刚度系数,Kc为联轴器、轴承和锥齿轮的刚度系数;Cl和Cs分别为负载和滚珠丝杠的阻尼系数,Cc为联轴器、轴承和锥齿轮的阻尼系数;Jl为负载质量,Js为滚珠丝杠的转动惯量,Jc为联轴器、轴承和锥齿轮的转动惯量;I3和I11分别为负载质量和滚珠丝杠的转动惯量的功率键合图元素,I16为联轴器、轴承和锥齿轮的转动惯量的功率键合图元素;R2和R10分别为负载阻尼系数和滚珠丝杠阻尼系数的功率键合图元素,R15为联轴器、轴承和锥齿轮阻尼系数的功率键合图元素;C5和C8分别为负载刚度系数和滚珠丝杠刚度系数的功率键合图元素,C13为联轴器、轴承和锥齿轮刚度系数的功率键合图元素;m为变换器模数;Se1为作用在滚珠丝杠螺母上的驱动力,Se17为发电机的电磁转矩．

2.2 状态方程

滚珠丝杠副馈能减震器的功率键合图模型中有6个储能元件, 其中惯性元件I3,I11,I16和容性元件C5,C13为积分因果关系,C8为微分因果关系．系统状态变量X=[p3q5p11q13p16]T, 输入变量U=[Se1Se17]T, 其中p3和p11分别为负载和滚珠丝杠的广义动量功率键合图元素,p16为联轴器、轴承和锥齿轮的广义动量功率键合图元素,q5和q13分别为第5和13键对应位移的功率键合图元素．

依据功率键合图推导状态方程的原则, 得到滚珠丝杠副馈能减震器的状态方程

根据滚珠丝杠副馈能减震器功率键合图模型的状态方程, 建立滚珠丝杠副馈能减震器的数学模型[15]

3 馈能减震器动态特性分析

3.1 虚拟样机模型

对滚珠丝杠副馈能减震器进行精确测绘, 得到各部件的尺寸和装配方式,采用SolidWorks软件建立三维实体模型, 转换格式后导入ADAMS, 并对关键运动部件添加运动约束．具体为滑块与导轨之间添加移动副约束, 滚珠丝杠与滚珠丝杠螺母之间添加螺旋副约束, 底座和导轨与地面固定, 底座和锥齿轮轴(竖直)与滚珠丝杠之间添加转动副约束,锥齿轮轴(水平)与齿轮箱输入轴之间添加转动副约束, 发电机输入轴与齿轮箱输出轴之间添加转动副约束．为了模拟滚珠丝杠副馈能减震器运动期间的真实条件, 在模型上施加阻尼、摩擦和外接负载,电磁阻力矩方向与发电机转子旋转方向相反,施加在发电机转子上．在30 mm的固定位移幅值和一定频率范围内, 用正弦振荡力激励滚珠丝杠副馈能减震器, 研究系统的动态特性．

3.2 基于键合图的动态特性仿真分析

根据键合图元和方块图单元的对应关系, 将滚珠丝杠副馈能减震器的功率键合图模型转换为滚珠丝杠副馈能减震器方块图[16], 如图4所示．图中v和w表示键上的流变量, 经过变换器F和v分别变换为T和w, 其中F1～F6为第1～6根键上的势变量,v2～v6为第2～6根键上的流变量,T7～T15和T17分别为第7～15和17根键上的势变量,w7～w16为第7～16根键上的流变量,s为时间函数的拉普拉斯变换．

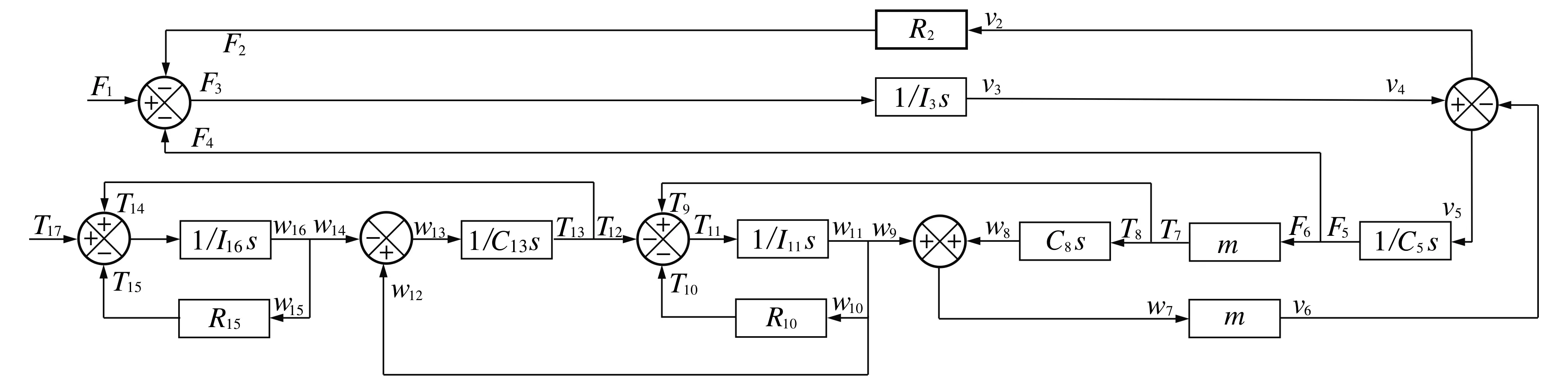
图4 滚珠丝杠副馈能减震器方块图Fig.4 Block diagram model of ball screw energy-harvesting shock absorber

采用MATLAB/Simulink中图形模块建模, 使用自定义模块表示每个键合图元[17]．阻性元件的框图单元用Gain模块表示, 0结和1结用Add模块表示,变换器用两个Gain模块表示, 具有积分因果关系的容性元件和惯性元件用积分模块表示, 具有微分因果关系的容性元件和惯性元件用微分模块表示[18]．根据上述规则, 构建滚珠丝杠副馈能减震器动态仿真模型, 如图5所示, 仿真参数详见文献[18]．本文采用ode45法求解, 运行仿真程序．

图5 滚珠丝杠副馈能减震器的动态仿真模型Fig.5 Dynamic simulation model of ball screw energy-harvesting shock absorber

图6为MATLAB/Simulink模块与虚拟样机仿真结果对比．由图6可得, 在相同加载条件下, MATLAB/Simulink模块与虚拟样机的动态仿真结果基本吻合,验证了动态模型的正确性,其中虚拟样机仿真结果的波动是由锥齿轮和滚珠丝杠螺母副啮合不良造成的[19]; 输出功率Pout随振动频率的增加而增大, 振动频率为1.0 Hz时, 峰值输出功率为6 W, 振动频率为2.5 Hz时,峰值输出功率为38 W．

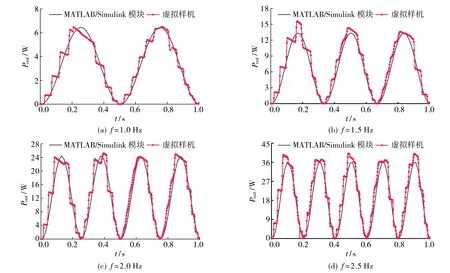
图6 MATLAB/Simulink模块与虚拟样机仿真结果对比Fig.6 Comparison of simulation results between Simulink module and virtual prototype

图7为外接电阻为5 Ω时不同频率下力随位移变化的关系曲线, 图中回路面积为滚珠丝杠副馈能减震器在一个循环中的输入功．等效阻尼系数[19]Ceq=W/(fl2π), 其中W为输入功, J;f为频率, Hz;l为位移, mm．由图7可知, 当位移振幅为30 mm, 阻尼力从频率为1.0 Hz时的136 N增加到频率为2.5 Hz时的340 N, 滚珠丝杠副馈能减震器输入功随振动频率的增加而增大, 阻尼力随等效阻尼系数的增加而增大．图8为位移振幅为30 mm, 频率为1.0 Hz时不同外接电阻下力随速度变化的关系曲线．由图8可知, 当外接电阻为50 Ω时, 阻尼力与速度近似呈线性关系,对应斜率为阻尼系数[19]; 随着外接电阻的减小, 阻尼力与速度呈非线性关系, 阻尼力随激励速度的增大急剧增加, 即在较小的外接电阻条件下, 激励速度越高, 减震器越硬; 阻尼力和阻尼系数随外接电阻增加而减小．

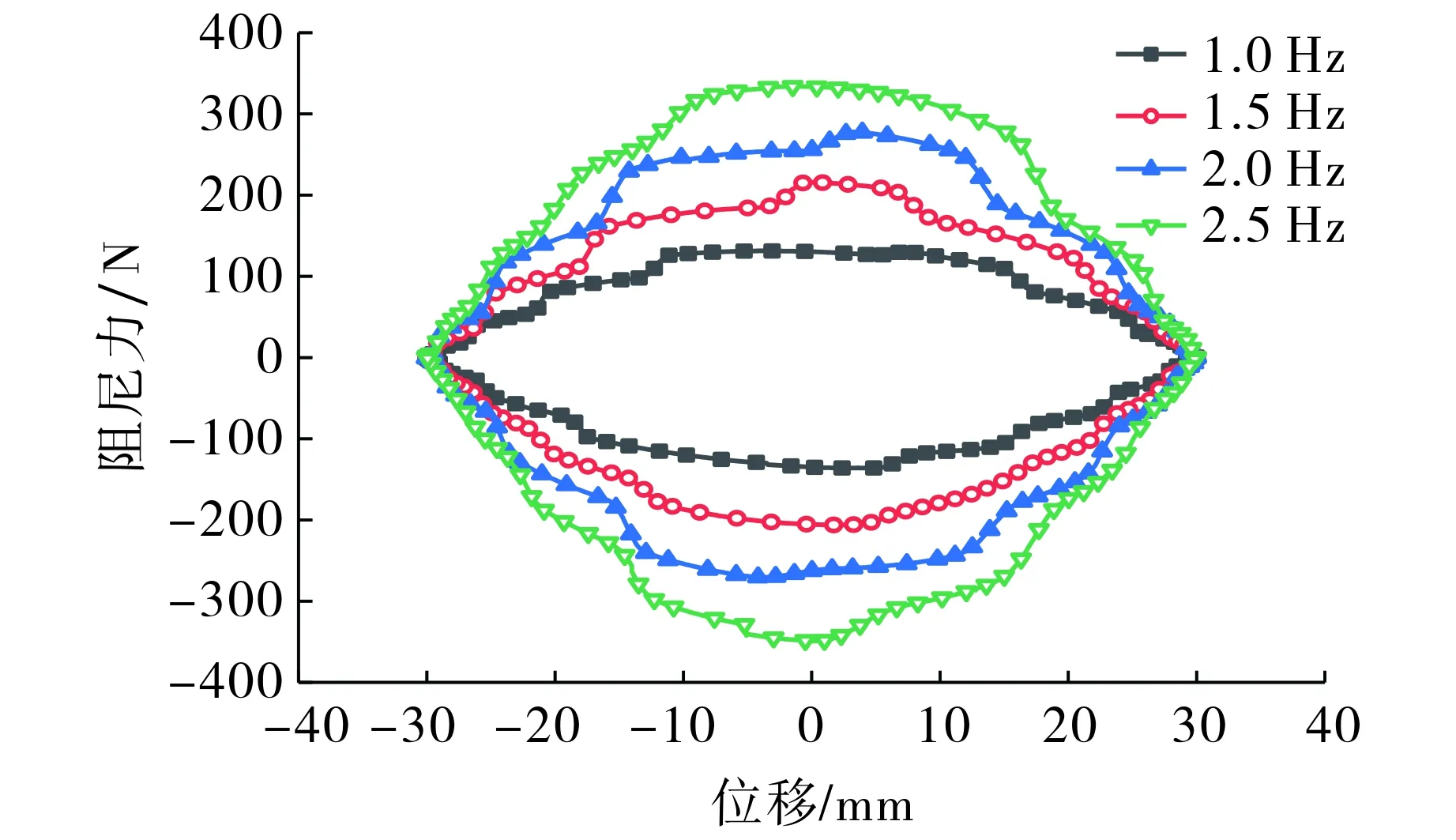
图7 不同频率下力随位移变化的关系曲线Fig.7 Diagram of force versus displacement at different frequencies

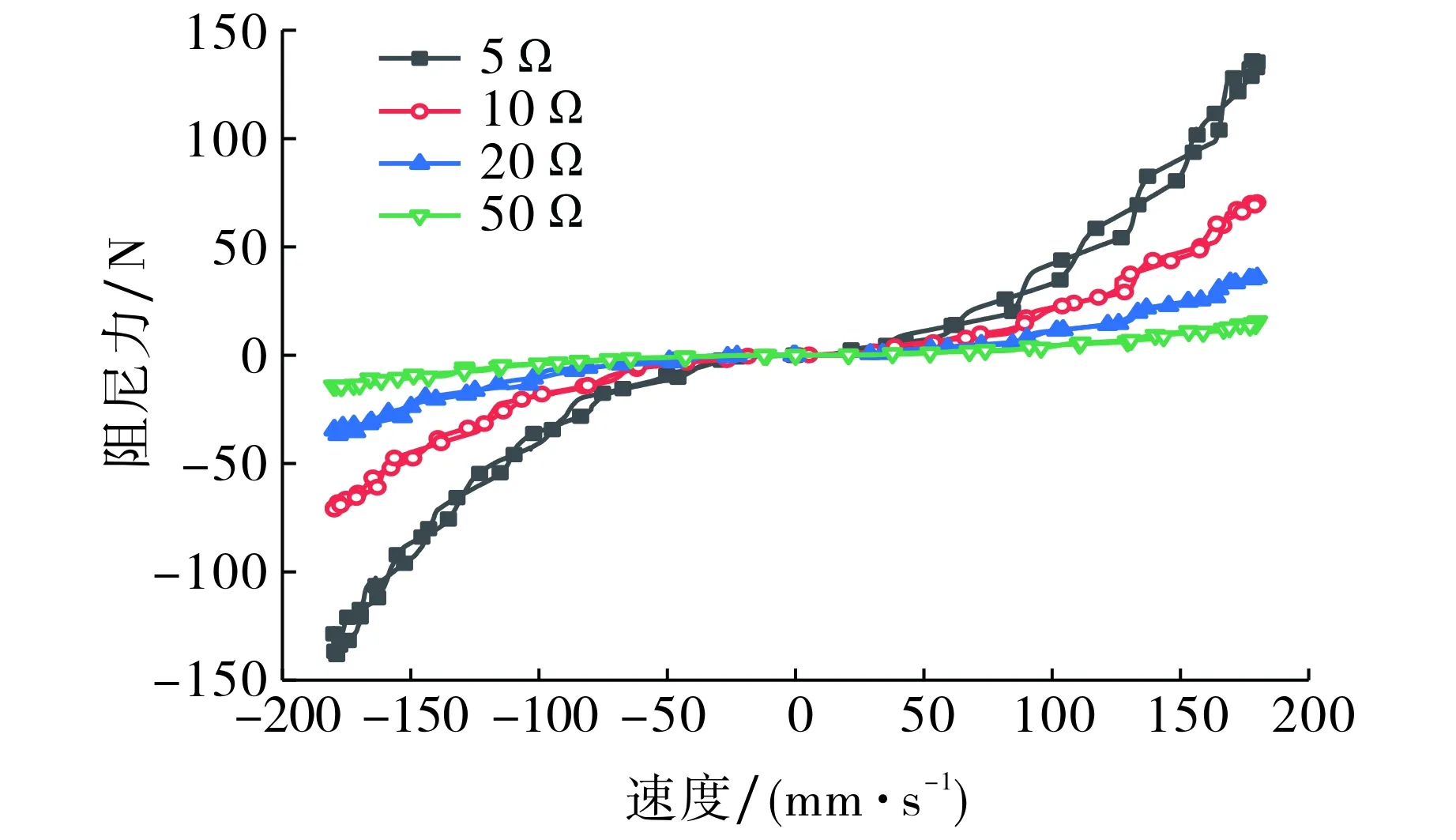
图8 不同外接电阻下力随速度变化的关系曲线Fig.8 Diagram of force versus velocity with different external resistance

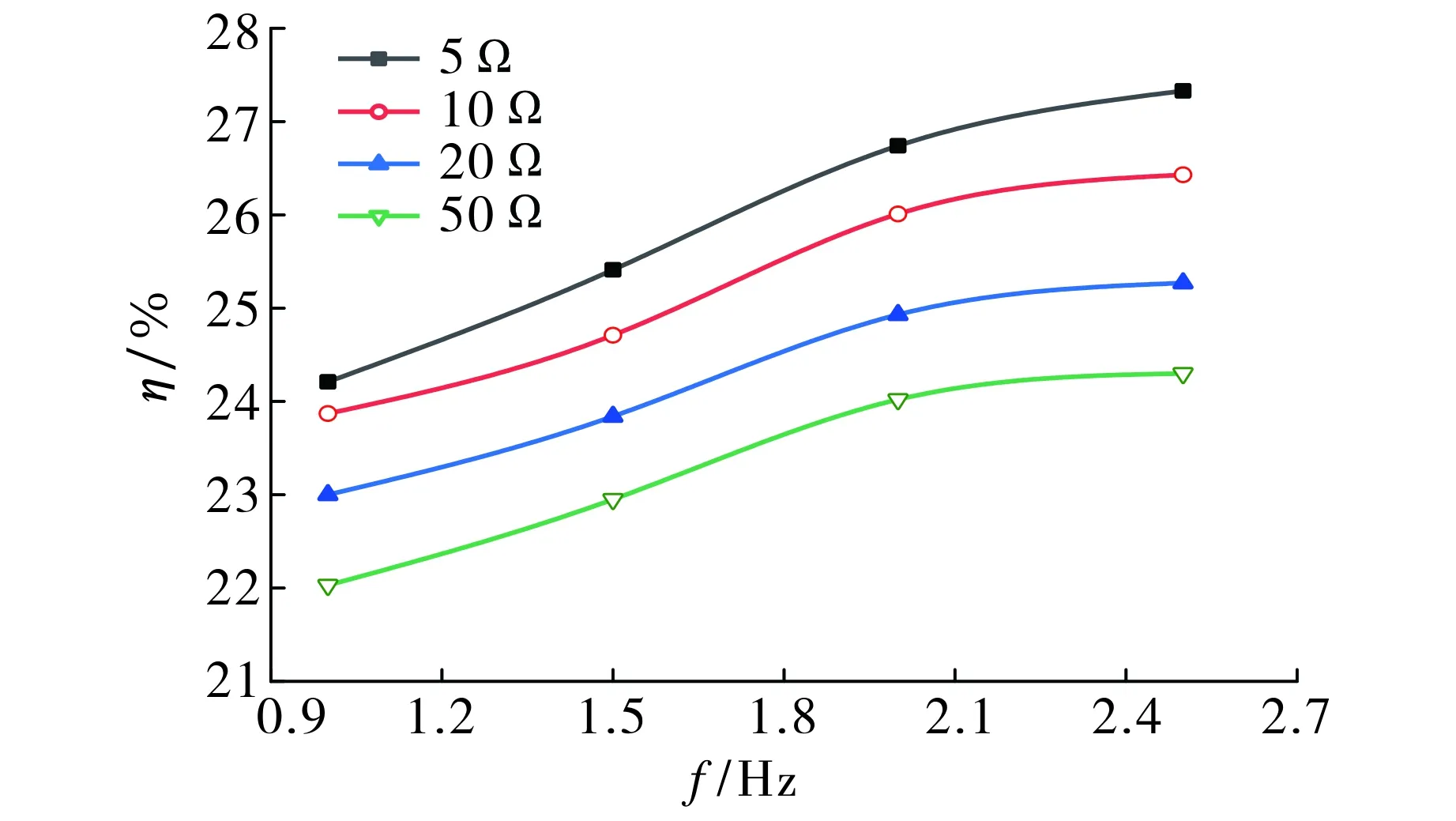
图9 回收效率Fig.9 The regenerative efficiency

回收效率是机械系统内部阻力和摩擦损失的直接衡量标准, 能量回收效率[20]η=Pout/Pin×100%, 其中Pin为输入功率．图9为振动频率和外接电阻对滚珠丝杠副馈能减震器回收效率的影响．由图9可得, 在外接电阻一定时, 回收效率随频率的增加而增加; 相同频率下, 外接电阻越小, 回收效率越高, 当频率为2.5 Hz时,外接电阻5 Ω的回收效率为27.33%, 外接电阻50 Ω的回收效率为24.3%．

4 结论

1) 功率键合图法可有效反映滚珠丝杠副馈能减震器的非线性特征, 便于构建复杂系统和修改仿真参数, 可直接导出结果, 提高了仿真效率．

2) 阻尼力和阻尼系数随外接电阻增加而减小; 外接电负载较低, 振动频率较高时, 阻尼力较大; 外接电负载一定时, 激励速度越高, 减震器的阻尼系数越大, 减震器越硬．

3) 基于滚珠丝杠副的馈能减震器具有较高的能量回收潜力,能量回收效率与振动频率呈正相关,与外接电负载呈负相关,当振动频率最大,外部电负载最小时,能量回收效率最高．