Banach空间中二阶非自治积微分方程的适度解

陈 燕, 范虹霞

(兰州交通大学数理学院, 兰州 730070)

本文主要讨论Banach空间E中二阶非自治积微分方程非局部问题

(1)

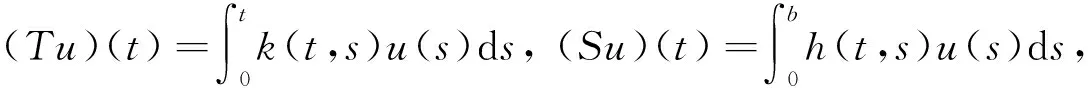
非局部问题首先是由Byszewski等[1]提出, 相比于经典的初值问题, 对许多有趣的自然现象非局部问题更易建模, 从而被广泛应用于物理等学科领域中而受到较多的关注[2-4]．此外, 类似于问题(1)以及其他更特殊的积微分方程常常应用于反应扩散方程、生物工程或者具有记忆性、黏弹性、遗传性等特殊性质物理材料的分析过程中[5-8], 许多学者对这类方程的各种性质进行了广泛的研究．由于研究该类方程其他性质的前提是得到其适度解存在性与唯一性, 故而研究其适度解的存在唯一性是非常必要的．Shi等[9]在非线性项f一致连续的情形下, 利用Sun等[10]推广的凸幂凝聚算子不动点定理, 研究了

这类一阶自治积微分方程初值问题整体适度解和正适度解的存在性．而非线性项f一致连续是非常强的假设, 本文拟减弱此要求, 并考虑在与A(t)相关的发展系统非紧的情形下, 利用凸幂凝聚算子理论及算子变换技巧, 讨论二阶非自治非局部问题(1)适度解的存在性．

1 预备知识

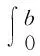
抽象的二阶非自治发展方程初值问题

(2)

其中A(t):D(A(t))⊂E→E是闭的稠定线性算子,f:J→E为适当定义的函数．对问题(2)适度解的研究都是基于与之对应的齐次发展方程

x″(t)=A(t)x(t),t≥0

(3)

生成的发展系统S(t,s), 下面给出所需的发展系统S(t,s)的定义．

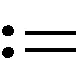
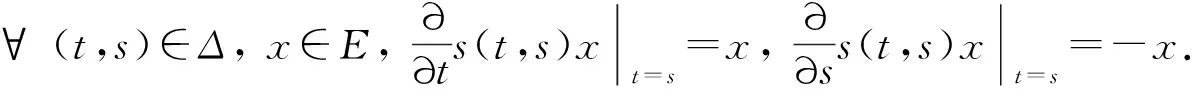
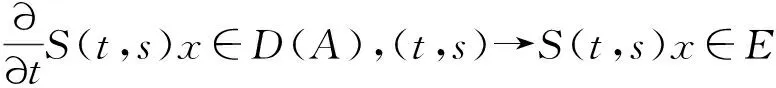
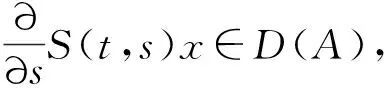
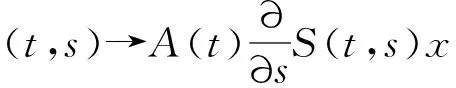
本文中, 假设与A(t)相关的发展系统S(t,s)存在, 那么存在N>0,使得对任意的s,t,s+h∈J,

‖S(t+h,s)-S(t,s)‖≤N|h|,

(4)

且有C(s,t)=-∂S(t,s)/∂s．记

(5)

以及

K0=max(t,s)∈Λ0|k(t,s)|,H0=max(t,s)∈Λ|h(t,s)|．

(6)

用α(·)表示E中有界集的Kuratowski非紧性测度,αC(·)表示C(J,E)中有界集的Kuratowski非紧性测度, 下面给出有关Kuratowski非紧性测度的一些性质与引理．

引理1[12]设X,Y是实Banach空间,B,C是X中的有界集, 则有下列性质:

1)B相对紧⟺α(B)=0;

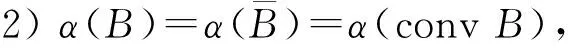
3) 若B⊆C,则α(B)≤α(C);

4)α(B+C)≤α(B)+α(C), 其中B+C={x+y:x∈B,y∈C};

5)α(B∪C)≤max{α(B),α(C)};

6)α(λ(B))≤|λ|α(B), 其中λ∈R;

7) 若映射Q:D(Q)⊆X→Y是Lipschitz连续的, 且Lipschitz常数为k, 则对任意有界集B⊆D(Q),α(Q(B))≤kα(B)．

引理2[10]若B⊂C(J,E)有界且等度连续, 则α(B(t))在J上连续, 且αC(B)=maxt∈Jα(B(t))．

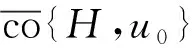
引理4[13]若B⊂C(J,E)有界, 则存在可数集B0⊂B, 使得αC(B)≤2αC(B0)．

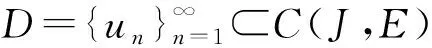
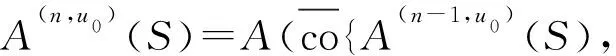
下面给出本文将要证明的问题(1)适度解的形式．

定义2对∀t∈J, 若函数u∈C(J,E)满足积分方程

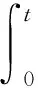
(7)

则称u是问题(1)的适度解．

令R>0为有限常数, 记BR={u∈E: ‖u‖≤R},ΩR={u∈C(J,E): ‖u‖C≤R}．

2 主要结果

本节主要讨论问题(1)适度解的存在性, 以下给出证明过程所需的假设．

(H1)f:J×E×E×E→E满足:f(t, ·, ·, ·)对t∈J几乎处处连续,f(·,u1,u2,u3)对ui∈E(i=1,2,3)强可测．gi:J×E→E,i=1,2为全连续函数．

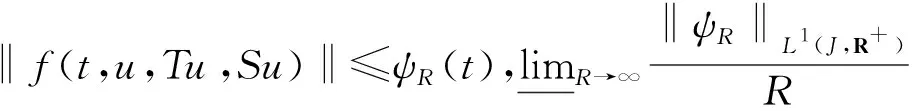
(H3) 存在常数Li>0(i=1,2,3), 使得对任意有界可数集Di⊂E(i=1,2,3), 且对几乎处处t∈J有α(f(t,D1,D2,D3))≤L1α(D1)+L2α(D2)+L3α(D3)．

(H4) 存在常数Lgi>0(i=1,2), 使得对∀u1,u2∈E, 有‖gi(u2)-gi(u1)‖≤Lgi‖u2-u1‖,i=1,2．

定理1若假设条件(H1)～ (H6)都满足, 则问题(1)在区间J上至少有一个适度解．

证明 定义算子Q:C(J,E)→C(J,E)满足

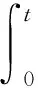
(8)

定义算子G:C(J,E)→C(J,E)满足

(Gu)(t)=u(t)-C(t,0)g1(u)-S(t,0)g2(u)．

(9)

显然,u(t)为问题(1)的适度解当且仅当u(t)为算子G-1Q的不动点．下证算子G-1Q存在不动点．

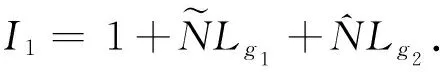
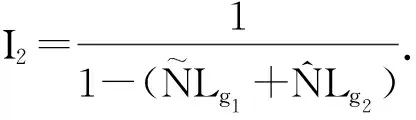
(Gu)(t)=u(t)-C(t,0)g1(u)-S(t,0)g2(u)=y(t),t∈J．

(10)

定义算子W:C(J,E)→C(J,E)为

(Wu)(t)=y(t)+C(t,0)g1(u)+S(t,0)g2(u),t∈J．

(11)

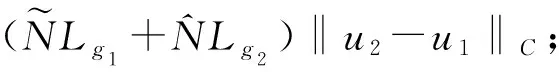
G-1y(t)=u(t)=y(t)+C(t,0)g1(u)+S(t,0)g2(u),t∈J．

(12)

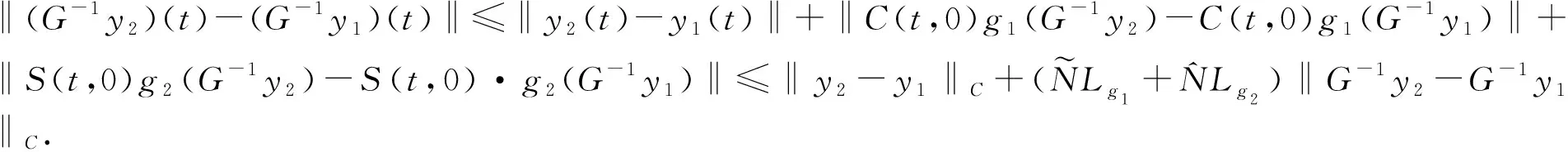
(13)

得‖G-1y2-G-1y1‖C≤I2‖y2-y1‖C．

第三步: 证明(G-1Q)ΩR⊂ΩR．对任意u∈ΩR, 令y=(G-1Q)u, 从而有Gy=Qu．由式(8), (9)可得

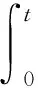
(14)

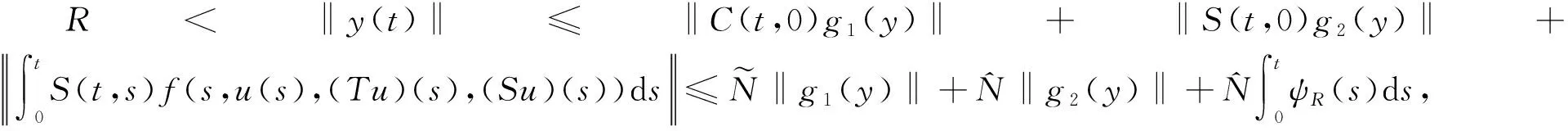
limn→+∞‖f(s,un(s),(Tun)(s),(Sun)(s))-f(s,u(s),(Tu)(s),(Su)(s))‖=0,

(15)

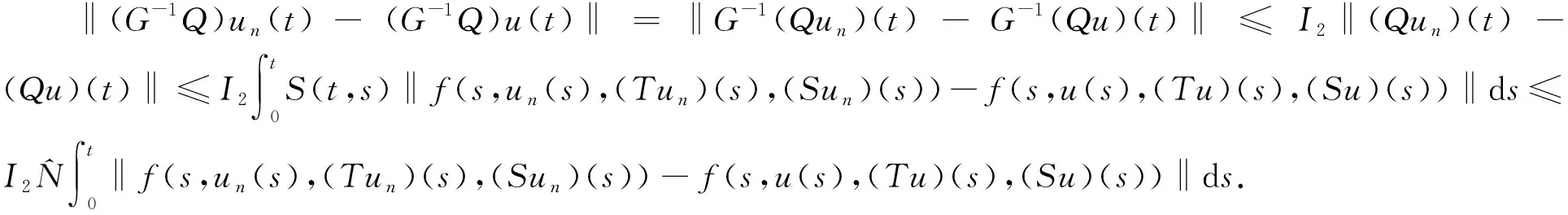
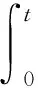
对任何D⊂F及u0∈F, 由(G-1Q)(n,u0)的定义及引理3可得(G-1Q)(n,u0)D⊂ΩR是等度连续集; 因此, 由引理2知

αC((G-1Q)(n,u0)D)=maxt∈Jα((G-1Q)(n,u0)D(t)) ,n=1,2,…．

(16)

α((G-1Q)D(t))≤2α((G-1Q)D1(t)) ．

(17)

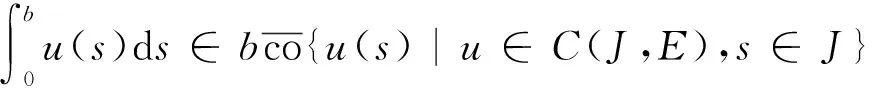
(18)

(19)

因此, 由式(17)～(19)、条件(H3)、引理1,3,5及非局部函数gi是紧的, 有

(20)

(21)

因此, 由式(18)～(21)、条件(H3)、引理1,3,5及非局部函数gi是紧的, 有

对任意t∈J, 假设

(22)

(23)

由式(18),(19),(22),(23)、条件(H3)、引理1,3,5及非局部函数gi是紧的, 有