世界优秀羽毛球男子单打后场技战术行动与成绩关系的研究
陈穗钦
1 前言
已有的对世界优秀羽毛球男子单打后场技战术研究中,有两个显著的结论,一是在羽毛球前、中和后场,后场技战术运用仅次于前场技战术,二是后场不同技术使用率,从高到低排列依次是杀球、吊球、高远球。
2012年伦敦奥运会林丹和李宗伟大战中,林-李的后场球比例分别为25.88%和32.87%。都达到25%以上的占比,仅次于前场技战术(王德平,2013);2017年世锦赛八强比赛统计分析结果表明:优秀男子单打运动员击球区域比例从高到低依次是前场51.8%、后场31.4%、中场16.8%(唐开悦,2018)。
对李宗伟和林丹30届奥运会决赛研究表明在后场技术运用中按高低顺序为:杀球占52%,吊球22%,高远球12%(高伟华和王德平,2013);单打选手林丹、李宗伟后场进攻技术的对比研究中杀球占71.1%和57.2%,吊球45%和52%,(姜来,2015);2017年世锦赛八强比赛统计结果显示后场技战术使用率依次为:杀球40.5%、吊球30.1%、高远球29.4%(唐开悦,2018)。
已有的研究揭示了后场技战术运用的一些特征,如后场技战术运用仅次于前场、各种技术使用频率排列为杀球-吊球-高远球。研究中存在的主要问题是:(1)多以个别的最优秀的运动员为研究对象,采用频数的统计方法分析数据,由于样本量较小,及研究者的意识,没有采用集中趋势和离散趋势来分析数据,因此研究虽为描述性研究,但研究的规范性限制了对特征的深入描述;(2)没有进一步探索羽毛球后场技战术运用的因果关系,以及由此形成的深层次的机理和规律,可认为这是制约竞技羽毛球运动发展的极为重要的原因之一。
2 结果与分析
美国《哈珀柯林斯社会学词典》对理论的定义是:理论是“由逻辑的或数学的陈述所连接的一组假设或命题,它对经验现实的某一领域或某一类现象提出解释”;理论是“以一种系统化的方式将经验世界中某些被挑选的方面概念化并组织起来的一组内在相关的命题”。
2.1 高远球与成绩关系的研究
后场高远球是由底线击至对方底线的一种高弧线飞行球。
后场高远球由于飞行弧线高,速度慢、到达对方底线所用时间较长,而且不易被对方拦截,因而它能迫使对方远离“中心位置”退到底线击球,在被动状态下运用此技术可为自己争取回位时间,以便过渡和调整击球位置,调整场上的比赛节奏,从而摆脱被动局面。
如图1所示,进攻队员p在右后场区打一拍正手直线高远球,防守队员就要从中场跑动至左后场区去回击高远球,回击的高远球可以是回直线、也可以回中线、同时也可以回大对角,落点如DP1、DP2、DP3。从图中可以看出,直线落点DP1、中线落点DP2、的跑动距离都在半场的范围之内,进攻队员可以做出很多的回球动作,并且回球质量也会很高,只有落点DP3的球在另一个场区,所以进攻队员跑动的距离是最远的,也是最被动的,回球质量也是最差的。此时落点DP3的球才有可能把被动的局势扭转。因此,我们假设:“在打高远球时,将球击到对手的反手位,高远球的得分就越高”。
统计结果表明(表1):(1)高远球落点次数(t)方面,运动员在D2t落点的平均数0次之间,D1t和D3t落点的平均数5~9次之间,(t=1.729,p=0.144,p>0.05),可认为差异无统计学意义;D1t和D2t、D2t-D3t处落点之间平均数差异明显,且达到显著性水平(D1t-D2t,t=5.171,p=0.004,p<0.05;D2t-D3t,t=7.201,p=0.001,p<0.05)。(2)高远球偏度得分(S2)方面,由于根据我们的判断,距离中场站位越远、接球难度越大,因此,区域D2接球最易、区域D1和D3接球最难,表1中D1t和D3t数据呈现出明显的趋势特点,直接支持我们这个观点。正是基于该观点,不同区域赋权后,区域D1s2-D3s2(t=-0.050,p=0.962,p<0.05)差异达不到显著性水平;区域D1s2-D2s2之间(t=5.171,p=0.004,p<0.05);区域D2s2-D3s2(t=-7.201,p=0.001,p<0.05)差异达到非常显著性水平。
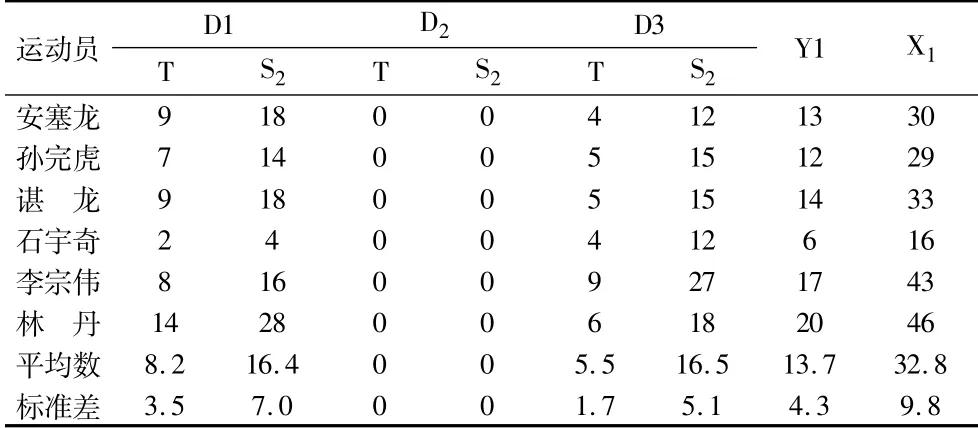
表1 运动员勾球落点及得分统计表
为了验证Y1(三个区域落点总次数)与X1(三个区域总偏度得分)之间的关系,本研究采用皮尔逊相关系数的方法进行计算。为此,首先做出两变量的散点图,以判断统计数据是否呈近似直线的关系,即检验本研究变量数据是否达到使用皮尔逊相关系数统计方法的要求。由散点图(图2)可知,高远球得分与高远球距离偏度总得分呈近似直线关系,因此,可采用皮尔逊相关系数r计算两变量的相关系数。
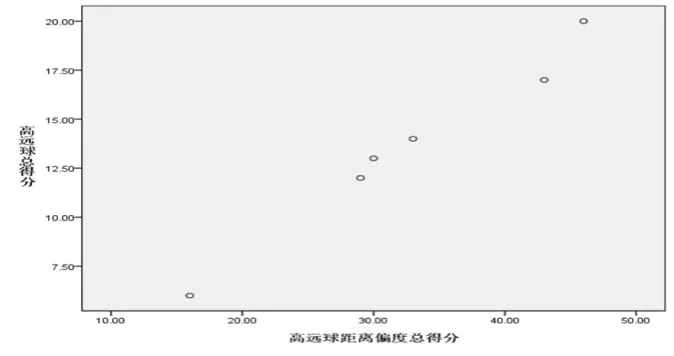
图2 运动员偏度得分与得分散点图
统计结果表明,Y1与X1之间达到高度相关(r=.991**,p<0.05),证实“在打高远球时,将球击到对手的反手位,高远球的得分就越高”的假设。
2.2 吊球与成绩关系的研究
后场吊球是将后场区域端线附近位置的球,回击到对方前场区域(前发球线附近与球网之间)紧靠边线两角的近网小球。它可分为正手吊球和反手吊球两种。
从图3中可以看出,进攻队员p可以在正手位右场区一个直线吊球落点为DP1,也可以斜线吊球落点为DP2,这两个落点的球对于站在中场防守的队员来说,距离基本是相等的。他回球的难易程度也差不多,但是对于进攻队员来说,正(反)手的直线吊球的操作难度比斜线吊球的难度大。所以一般为了减少自己的主动失误,保持主动的局面,在场上都会采用较容易操作又保险的技术动作。因此,我们假设:“后场吊球采用高手位主动吊球,击球线路为斜线(落点为DP2),吊球的得分就越高”。
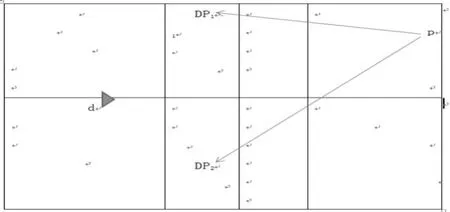
图3 后场吊球的落点及防守队员的站位示意图
吊球落点次数(t)方面,运动员在D1t和D2t处落点的平均数8~10次之间,(t=-0.672,p=0.531,p<0.05),可认为差异无统计学意义。这检验结果与我们的预期假设不一致,为了再次验证数据,我们对接球区域难易程度进行赋值。
吊球偏度得分(S2)方面,由于根据我们的判断,正(反)手的直线吊球的操作难度比斜线吊球的难度大,因此,区域D1吊球难度大、区域D2吊球容易,易得分。不同区域赋权后,区域D1s2-D2s2(t=-3.433,p=0.019,p<0.05);差异达到显著性水平。
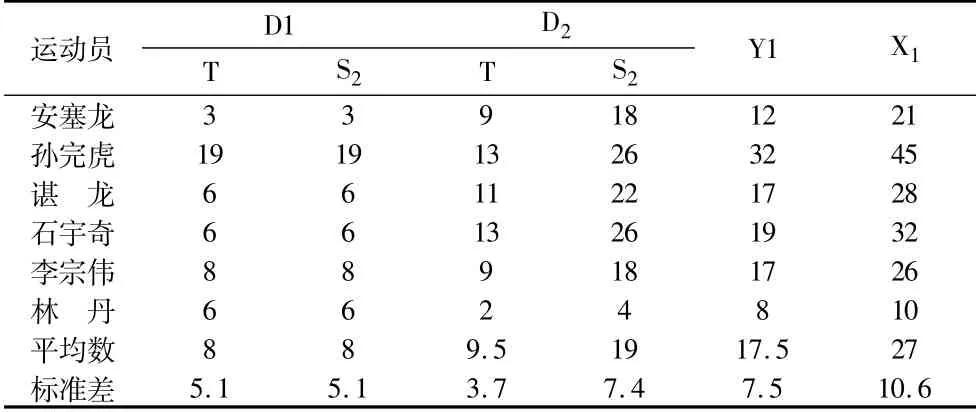
表2 运动员吊球落点及得分统计表
由散点图(图4)可知,吊球得分与吊球距离偏度总得分呈近似直线关系。因此,可采用皮尔逊相关系数r计算两变量之间的相关系数。
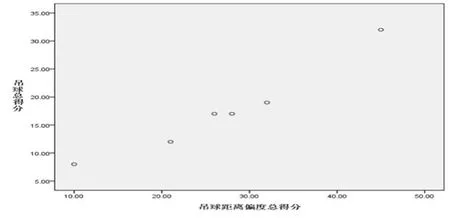
图4 运动员偏度得分与得分散点图
相关分析表明(表3),吊球落点距离偏度总得分与吊球得分相关系数r=.975**(p<0.05),表明吊球得分与吊球落点距离偏度总得分呈高度正相关关系,证实“后场吊球采用高手位主动吊球,击球线路为斜线(落点为DP2),吊球的得分就越高”。

表3 吊球得分与吊球距离偏度总得分相关系数
2.3 杀球与成绩关系的研究
后场杀球是针对对方击至后场或中场区域的来球,争取尽量高的击球点,将球由高而下地想对方场区全力扣压过去的一种球,采用高手位击球。
从图5中可以看出进攻队员在正手位的一拍杀球可以有四种选择,可以直线短杀落点为DP1,也已直线长杀落点为DP2,同时还可以选择斜线短杀落点为DP4,还可以选择斜线长杀落点为DP3。对于落点DP1和落点DP4的杀球,防守队员上一步就可以将球救回,但是对于落点为DP2和DP3靠近边线的长杀,防守队员对于这种情况完全是属于被动局势。很有可能是直接失分的。所以在后场杀球中,靠近边线的重长杀更有威力。因此,我们假设:“后场杀球越靠近边线,落点越靠近底线的高手位重长,杀球的得分就越高”。
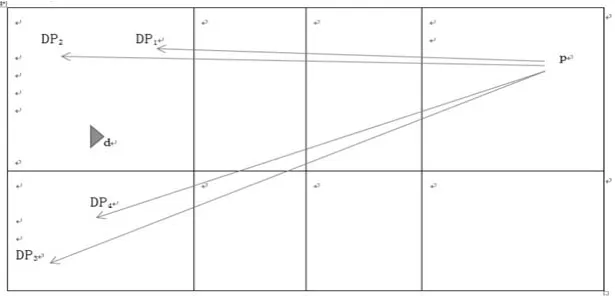
图5 后场杀球的落点及防守队员的站位示意图
杀球落点次数(t)方面,运动员在D1t和D4t和D2t和D3t处落点的平均数8~38次之间,落点之间平均数差异明显,且达到显著性水平(t=-23.606,p=0.000,p<0.05)。
杀球偏度得分(S2)方面,由于根据我们的判断,距离中场站位越远、接球难度越大,因此,区域D1接球最易、区域D3接球最难,表4中D3t数据呈现出明显的趋势特点,直接支持我们这个观点。正是基于该观点,不同区域赋权后,区域D1t和D4t和D2t和D3t(t=-38.363,p=0.000,p<0.05)差异达到非常显著性水平。
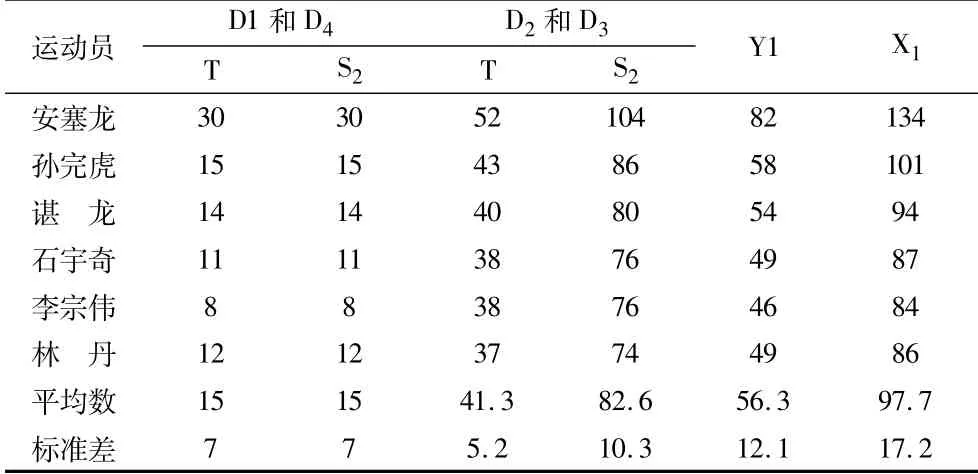
表4 运动员勾球落点及得分统计表
由散点图(图6)可知,杀球得分与杀球距离偏度总得分呈近似直线关系。因此,可采用皮尔逊相关系数r计算两变量之间的相关系数。
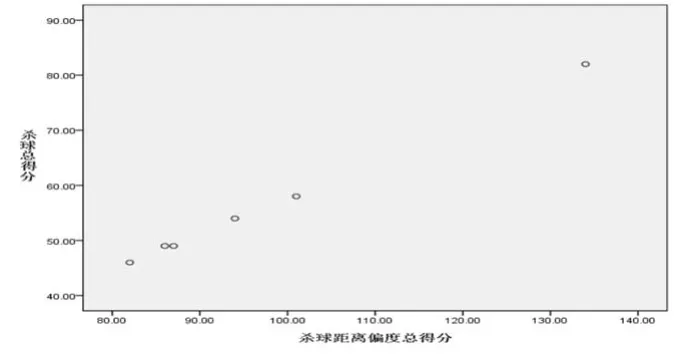
图6 运动员偏度得分与得分散点图
相关分析表明(表5),杀球落点距离偏度总得分与杀球得分相关系数r=.999**(p<0.05),表明杀球得分与杀球落点距离偏度总得分呈高度正相关关系,证实“后场杀球越靠近边线,落点越靠近底线的高手位重长,杀球的得分就越高”。

表5 杀球总得分与杀球距离偏度总得分相关系数
3 结论
3.1 在30场71局的比赛中,针对运动员后场技战术行动进行分析,后场技术使用率从高到低依次是杀球、吊球、高远球。但是其中高远球属于防守类型的技战术,不是主要的得分手段。虽然不是主要的得分手段,但是只要高远球技术过硬,依然影响着后场技战术行动与成绩之间的关系。
3.2 对世界优秀羽毛球男子后场单打技战术行动与成绩关系的观察统计与皮尔逊相关系数计算分析,以及配对样本T检验的统计方法进行验证,证实了以下假设是成立的:
3.2.1 证实了“在打高远球时,将球击到对手的反手位,高远球的得分就越高”。
3.2.2 证实了“后场吊球采用高手位主动吊球,击球线路为斜线(落点为DP2),吊球的得分就越高”。
3.2.3 证实了“后场杀球越靠近边线,落点越靠近底线的高手位重长,杀球的得分就越高”。

