创新型人力资本、全要素生产率与高质量发展——以长三角地区为例

罗 芳，陈久爱，凌 晨

（上海理工大学 管理学院，上海 200093）

人力资本理论表明，人力资本积累是技术进步的重要源泉，人力资本水平对于全要素生产率的提升具有重要的作用，创新越来越成为经济发展的决定性因素。随着长三角区域的一体化和扩容，长三角地区经济高质量发展面临巨大的瓶颈，同时长三角地区又作为高级人才集聚的区域。因此，本文研究创新型人力资本、全要素生产率和经济高质量发展之间的关系对于增强创新动力促进长三角区域经济高质量发展具有重要的现实意义。

一、文献综述

人力资本理论最先是由舒尔茨所提出的，是体现在劳动者身上的资本，人力资本也可以分为一般人力资本和高质量人力资本，高质量人力资本即为具有高知识水平比一般人力资本更高级的劳动力，在研究过程中创新型人力资本这一概念逐渐被提出代表高质量的人力资本。Raszkowskia（2015）[1]认为创新型人力资本能够利用知识积累形成的智慧思维设计出高效、准确的创新方案，从而克服困难、突破发展瓶颈，并以智慧的眼光观察周围世界，有效地借助外部手段解决自身问题。国内学者普遍认为，创新型人力资本具有普通劳动力缺少的创新特质，能实现生产要素和资源的有效配置、带来技术效率的显著提升，以边际报酬递增和产出乘数效应克服物质资本和劳动的边际报酬递减效应带动经济的持续增长，是推动中国经济高质量发展的关键[2]。根据内生增长理论，全要素生产率是指经济增长中不能被要素投入资本和劳动所解释的那部分，并且资本和劳动并不能带来持续的经济增长，全要素生产率一般代表技术进步，技术进步才能带来经济的持续增长。全要素生产率即可用来衡量某个地区的经济发展绩效。现有的观点普遍认为创新型人力资本存量能够有效提高区域的创新能力，通过技术创新这一机制促进区域经济增长，提高全要素生产率。陈俊杰和钟昌标（2020）[3]认为较高级的创新型人力资本以创新的方式推动经济增长，然而目前仍然是一般人力资本以数量型驱动经济增长方式为主，创新型人力资本是当前经济增长的核心动力。景维民等（2019）[4]认为高级的教育人力资本结构有助于技术的转型和升级促进经济高质量发展，只有抢占人才高地的区域才能更好实现经济高质量发展。高质量发展首要的还是经济效益的提升，要想实现高质量发展，最为关键的因素就是实现全要素生产率的提升，全要素生产率的提升意味着资源得到有效配置、社会生产效率得到有效提高，资源配置和生产就是提升经济发展质量的关键步骤[5]，全要素生产率是创新效率的直接反映，而创新是经济发展的动力源泉，全要素生产率提升自然也是经济高质量发展的关键推动力。

从现有文献来看，创新型人力资本理论是在人力资本理论的基础上形成的，在索罗内生经济增长的理论基础上形成了全要素生产率测算体系，较多学者研究了人力资本对于经济发展的促进作用，然而较少学者研究某个区域创新型人力资本与全要素生产率之间的相关关系程度，并将经济高质量发展结合起来的研究也相对较少。长三角是中国经济最具活力的区域，随着长三角一体化和扩容，资源集聚带来的经济发展优势逐渐转为资源环境承载能力不足的劣势，突破长三角一体化高质量发展瓶颈是现在亟需解决的问题。

二、作用机制

由人力资本理论和内生经济增长理论可得，全要素生产率是不能被生产要素投入劳动和资本等解释的那部分产出增长率，通常指的是技术进步率，并由柯布道格拉斯生产函数可得，产出是由劳动力结合物质资本生产所得，人力资本是指具有高知识水平的劳动力，必须体现在劳动力身上，全要素生产率一般代表技术进步率，人力资本是推动技术创新的重要决定因素，技术进步是经济持续增长的主要动力。现有的观点普遍认为人力资本积累带来人力资本水平提升，创新型人力资本是比一般人力资本更高级的人力资本，是创新推动技术进步的驱动力，能够有效提升区域的创新能力，通过技术创新这一机制提升全要素生产率，促进经济高质量发展。韩静等（2019）[6]利用安徽省时间序列数据实证研究发现创新型人力资本显著地促进了经济增长。刘悦等（2018）[7]对山东的经济发展贡献率进行实证研究，得出创新型人力资本通过提升知识水平促进创新，推动经济增长，创新型人力资本对经济发展有着巨大的贡献。刘志彪和凌永辉（2020）[8]认为高质量发展的关键在于全要素生产率的提升，全要素生产率的提升与高质量发展创新、协调、绿色、开放以及共享的内涵是完全一致的1。由现有文献可得，创新型人力资本是创新的决定性因素，可以通过自主创新、模仿创新等开展技术创新活动，推动劳动密集型产业不断向资源密集型产业转型，提高资源配置效率，提升劳动生产率，促进全要素生产率提升，进而推动经济高质量发展。因此，创新型人力资本对于长三角区域经济高质量发展具有重要的推动作用。

三、模型构建和指标选取

由前人文献可得，计算全要素生产率的方法有随机前沿分析SFA 方法、数据包络分析法、索罗核算法等，本文根据柯布道格拉斯生产函数基于OLS最小二乘估计估算全要素生产率。由柯布道格拉斯生产函数Yit=AitKitαLitβ，对其取对数可得线性模型如式（1）所示。

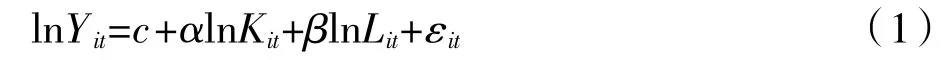
这里Yit代表i城市t年内的产出，Kit代表i城市t年内的物质资本存量，Lit代表i城市t年内的劳动投入。α是资本的产出弹性系数，β是劳动力的产出弹性系数，其中Ait=Yit/（KitαLitβ）。

（一）测算指标选取

由于某些城市个别数据缺失，本文选取长三角地区三省一市（上海市、江苏省、浙江省、安徽省）的24 个主要城市2000—2017 年的统计数据来分别表示各项指标数值进行定量分析。以2000 年作为基期，用消费者价格指数对数据进行平减，个别城市未找到居民消费者价格指数用城市居民消费者价格指数代替，产出指标用实际GDP 代替，用固定资产投资代表资本投入指标，物质资本存量测算参考前人文献运用永续盘存法Kit=Iit/Pit+（1-δ）Kit-1来测算，2000 年基期物质资本存量参考前人文献K0=I0/（g+δ），g为固定资产投资的平均几何增长率，折旧率Γ设定为9.6%，用社会从业人员代表劳动投入指标。

（二）模型构建

根据所构建的生产函数，A代表全要素生产率，全要素生产率受到创新型人力资本和其他因素的影响，其中Hc表示创新型人力资本，由于全要素生产率还受到除了创新型人力资本以外的因素的影响，本文还选用其他影响因素作为控制变量X加入模型。本文选取全要素生产率作为核心被解释变量，创新型人力资本作为核心解释变量构建面板模型如式（2）所示。

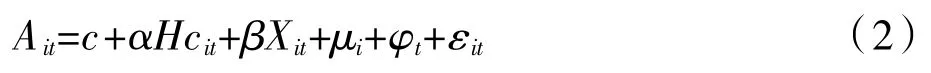
c表示常数项，α表示创新型人力资本系数，β表示其他解释变量系数，Γi表示城市固定效应，Γt表示时间固定效应，εit表示随机扰动项。

（三）变量选取与测算

被解释变量全要素生产率A 由OLS 最小二乘估计测算出，创新型人力资本（Hc）参考前人文献做法，利用受高等教育从业人员总工资收入计量创新型人力资本。参考前人文献[9]，根据对各类人员工资的测算结果可以确定高等教育就业人员工资水平为全部从业人员平均工资的1.5 倍，创新型人力资本这一指标由总体从业人员平均工资的1.5 倍来代表。除了创新型人力资本以外，全要素生产率还受到其他因素的影响，本文根据已有理论和现有文献选取政府规模（gov），本文设定政府财政支出额与GDP比值代表政府规模指标作为控制变量，创新型人力资本水平和全要素生产率政府规模指标都具有极强的城市固定特征和时间特征，本文分别引入城市和时间虚拟变量来表示个体以及时间固定效应，模型如式3 所示。数据来源中国统计年鉴、中国劳动力统计年鉴、各城市统计年鉴，个别数据缺失用线性插值法粗略估算得出。

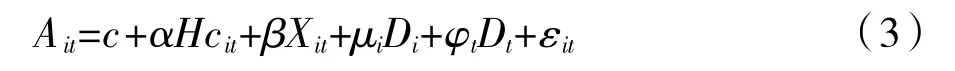
（四）测算结果分析

本文根据所选城市变量2000—2017 年的数据对全要素生产率进行测算，对基于柯布道格拉斯生产函数构建的模型分别进行混合回归、固定效应以及双向效应回归，根据回归结果可以看到，模型应该不存在个体以及时间的固定效应，混合回归结果如表1 所示，可以看到回归结果是非常显著的，利用A=Y/（K琢Lβ）测算出全要素生产率。由模型性回归结果可得。

表1 基于柯布道格拉斯生产函数的OLS 回归结果

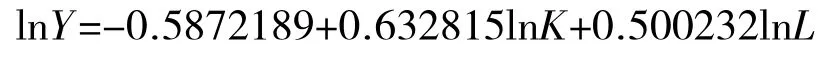
α的估计值为0.632 815，β的估计值为0.500 232，因此全要素生产率A=Y/（K0.632815*L0.500232）。表2 是对本文所选取和测算变量的说明与统计描述，由测算结果可知，长三角地区24 个城市全要素生产率存在显著差异，同样长三角地区创新型人力资本水平也存在显著差异，创新型人力资本水平最高的为13.658 36 万元，最低的只有0.888 6 万元。排名在前列的主要为上海、杭州、苏州、南京等城市，这说明创新型人力资本水平和全要素生产率水平存在明显的正相关关系，通过比较创新型人力资本水平和全要素生产率的变化情况，发现全要素生产率的变化情况并不显著，可以得出创新型人力资本水平提升对于全要素生产率的提升作用程度不够明显。

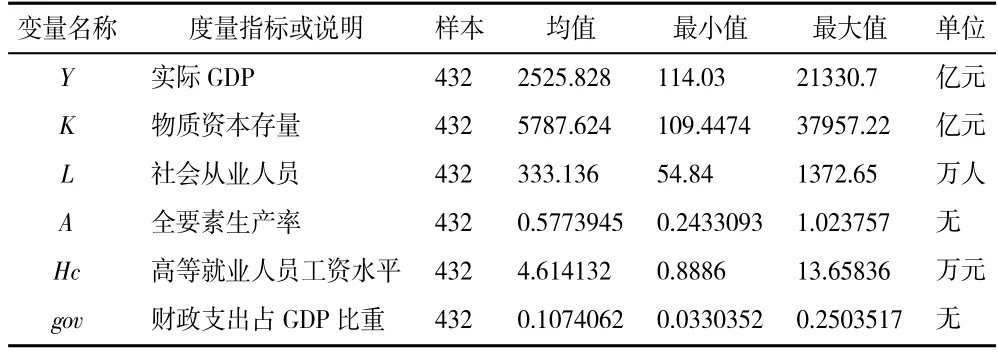
表2 数据说明与变量统计描述

四、实证分析

（一）主要回归结果

本文基于长三角地区24 个城市2000—2017 年的数据，把创新型人力资本变量作为核心被解释变量对模型进行回归，由于创新型人力资本和全要素生产率都带有极强的城市和时间特征，本文分别对原模型进行回归以及对引进城市和时间虚拟变量的模型回归，表2 分别报告了未引入虚拟变量、引入城市虚拟变量、时间虚拟变量以及同时引入城市和时间虚拟变量的回归结果，由回归结果可以看到，除了核心解释变量在单独引入城市虚拟变量模型中表现不显著，其他变量回归结果都是统计显著的，可以看到，同时引入城市和时间虚拟变量的模型回归结果是统计显著的，城市虚拟变量和时间虚拟变量的系数大部分在统计上都是显著不为0 的，且模型拟合程度也最高，可以得出创新型人力资本对全要素生产率的影响具有城市和时间特征。由回归结果可以得到，创新型人力资本对全要素生产率是存在正向促进作用的。

（二）内生性偏误与GMM 估计

本文选用全要素生产率作为核心被解释变量，创新型人力资本作为核心解释变量，这两个变量之间可能存在双向因果关系，创新型人力资本会影响全要素生产率，全要素生产率增加可能反过来会对创新型人力资本产生促进作用，模型可能存在内生性偏误问题。因此，本文选取核心解释变量创新型人力资本的滞后一阶作为工具变量进行GMM 估计[10]，结果如表4 所示。表4 结果显示的是将滞后一阶的核心解释变量加入模型1 的混合回归结果，与表3模型1 结果相比，可以看到核心解释变量系数更加显著，系数绝对值相差不大，略微较小，模型拟合优度更高。但从总体来看，模型回归结果是一致的，之前的估计可能对创新型人力资本对全要素生产率的影响略有高估，并由豪斯曼检验结果可得，模型不能拒绝所有解释变量均为外生的原假设。因此，可以认为，模型在一定程度上不存在内生性问题，回归结果是可靠的。并且回归结果与预期一致，长三角地区创新型人力资本能够促进全要素生产率的提升，然而目前阶段，创新型人力资本对全要素生产率的促进程度还不够。加大创新型人力资本投入能够推动技术进步，进而推动长三角地区经济高质量发展。可以看到，政府规模与全要素生产率呈负向的相关关系，本文这里的政府规模指的是财政支出与GDP 的比重，这可能因为财政支出占GDP比重太大，投入到科技创新行业的支出并不多，也可能政府对市场经济干预过多，反而会对经济产生负面的影响。

表3 创新型人力资本影响全要素生产率的主要回归结果

表4 创新型人力资本影响全要素生产率的GMM 估计

五、主要结论及政策启示

本文利用长三角地区24 个主要城市2000—2017 年的面板数据考察了创新型人力资本水平对全要素生产率的影响，进而分析了全要素生产率和经济高质量发展的协同关系，综合各种分析结果，得出以下结论：长三角地区创新型人力资本水平发达地区与欠发达地区差距较大，全要素生产率水平存在显著差异，欠发达地区创新型人力资本水平和全要素生产率均较低。创新型人力资本水平提升能够推动全要素生产率提升，全要素生产率提升是经济高质量发展的关键性一环，因此，创新型人力资本水平是经济高质量发展的关键因素；政府规模对全要素生产率提升作用并不显著，由此可见，财政支出并不是推动经济高质量发展的关键性因素，这可能是由于财政支出并没有得到合理有效的分配。基于上述结论，提出以下政策建议：长三角是人才集聚、资源集聚的区域，要利用资源和人才优势，加大创新型人力资本投入，给予高等教育从业人员比一般从业人员更高的工资水平，吸收更多的创新型人才，同时也要建立区域人才联合培养机制，使人才在区域内得到有效流动和配置。政府也应加大对教育、科技研发等相关领域的资金投入，将财政支出更多地转移到教育科研领域，培养出更多创新型人才，使人才成为创新的引领者、主导者，提高区域创新水平，推动供给侧结构性改革，促进经济发展；政府也要引导创新型人力资本水平较高的发达地区带动欠发达地区的发展，促进长三角区域一体化，推动长三角地区经济高质量发展。