低合金钢海水腐蚀监测中的双率数据处理与建模
陈 亮,付冬梅
1) 北京科技大学自动化学院,北京 100083 2) 北京市工业波谱成像工程中心,北京 100083
在海水腐蚀领域,由于海水环境的强腐蚀性,材料在服役过程中会不可避免地产生腐蚀现象,进一步导致其性能下降直至失效,从而带来巨大的经济损失和安全隐患[1].随着在线监测技术的发展,对材料的腐蚀状态进行实时监测变得更加容易[2].通过高灵敏度的前端传感器可以采集得到大量的腐蚀数据[3−4],但由于客观因素的影响,材料所处的海水环境数据采样频率与腐蚀数据的采样频率通常不一致,从而形成了具有不同采样频率的系统.这种输入输出量存在多个采样频率的系统称为多率系统,仅有两种不同采样频率的多率系统称为双率系统,对应的采样数据就是双率数据[5].因此,如何处理低合金钢海水腐蚀实验中的双率数据并准确预测钢材腐蚀状态对于指导腐蚀防护工作具有重要意义.
双率系统建模问题最早在系统辨识领域得到研究.Kranc[6]提出了切换分解技术,其思想是将多率系统转化为单率系统后进行分析.Friedland[7]和Khargonekar等[8]将切换分解技术发展完善为提升技术,成为了双率系统研究的最常用方法[9].Li等[10]采用提升技术和推理控制结果研究了双率系统的性能以及鲁棒性.Ding和Chen[11]应用提升技术提出了一种双率系统的递阶辨识方法.然而基于系统辨识的双率系统建模方法需先假定被辨识模型的结构形式,难以适用于结构未知的复杂非线性情况,因此需要提出一种不依赖模型结构的双率系统建模方法.
在腐蚀研究领域,均值法是常用的将双率腐蚀数据转化为单率数据的处理方法.Zhi等[12]将相对湿度、pH值、二氧化硫浓度、氯离子浓度等小采样周期的大气环境数据用均值法统一成与碳钢腐蚀速率相同的以年为采样周期的单率数据,然后建立了环境因子与腐蚀速率之间的预测模型.石雅楠等[13]对温度、相对湿度、PM2.5等以小时为采样周期的气象数据采用均值法进行处理,将双率采样数据转换为以天为采样周期的单率数据.Wei等[14]采用均值法对材料海水腐蚀电位数据进行处理并建立了海水腐蚀预测模型.
在将双率腐蚀数据转化为单率数据后,人工神经网络(Artificial neural networks, ANN)和支持向量回归 (Support vector regression, SVR)是常用的腐蚀建模方法.刘学庆等[15]采用电化学方法测定了3C钢在不同海水环境参数下的腐蚀速度,并根据四层误差反传神经网络(Back-propagation neural network, BPNN)分析了3C钢腐蚀速度与海水环境参数的相关性,建立了3C钢在海洋环境中腐蚀速度的预测模型.Shirazi和Mohammadi[16]结合帝国主义竞争算法 (Imperialist competitive algorithm, ICA)和ANN建立了海水环境与钢材腐蚀速率间的ICA−ANN预测模型,该模型在测试集上的均方误差约为0.01,平均绝对误差为0.011,拟合优度为0.99,能够较好地预测3C钢在海水环境下的腐蚀速率.Wen等[17]利用粒子群算法优化SVR的参数,建立了3C钢在海水环境下的腐蚀速率预测模型,并与BPNN进行了对比,结果表明SVR的泛化能力优于BPNN,可以对海水环境下碳钢的腐蚀进行跟踪.毕傲睿等[18]采用主成分分析方法对影响海水管道腐蚀的因素进行优选,然后将贡献率大的腐蚀因素作为SVR的输入,以腐蚀速率作为输出,建立管道腐蚀预测模型,然后通过鲇鱼粒子群算法对SVR进行优化,预测精度较高.
目前,在对双率腐蚀数据的处理方法中,均值法应用广泛,然而均值法不可避免地会忽略掉小采样周期数据中的细节信息,从而导致建模精度下降[19].同时,在腐蚀模型的构建中,基本选择ANN或SVR作为学习模型,而忽略了ANN容易陷入局部极小以及SVR预测精度低的问题.针对以上问题,本文以低合金钢海水环境下的双率腐蚀数据为例,对于材料腐蚀电位数据采样周期远小于海水环境因子数据的情况,提出了一种基于综合指标值 (Comprehensive index value, CIV)并结合改进相关向量回归 (Improved relevance vector regression, IRVR)的数据处理和建模方法.首先通过定义CIV来表征海水环境因子的综合影响,建立CIV与海水腐蚀电位的线性回归模型对双率数据进行填补,能够保留更多的原始数据信息,最终得到用于建模的单率数据集.最后,采用高斯核和二次多项式核构建IRVR的组合核,建立低合金钢海水腐蚀电位的预测模型CIV-IRVR,解决了数据信息损失和建模精度低的问题,为低合金钢海水腐蚀监测中双率数据处理和建模提供了一种新的思路及方法.
1 双率腐蚀数据
1.1 数据来源
本文数据来源于国家自然环境腐蚀平台三亚海水站的14种海洋工程中常用低合金钢(LAS1~LAS14)的海水浸泡实验,实验时间为2017年2月15日至2017年6月25日,其中低合金钢海水腐蚀电位数据和海水环境数据构成了双率腐蚀数据.LAS1~LAS14低合金钢的牌号依次为Q235、Q345DZ35、D36、Q345B、921、Q450NQR1、X70、X80、E690、E460、Prue Q235、Super fine grain steel 1、Super fine grain steel 2 以及 Micro-alloy steel.
1.2 低合金钢化学元素含量
14种低合金钢所包含的化学元素成分(Fe除外)共有 15种,包括 C、Si、Mn、P、S、Ni、Cr、Mo、Cu、Al、Ti、Nb、V、B以及 N,其含量如表1所示.
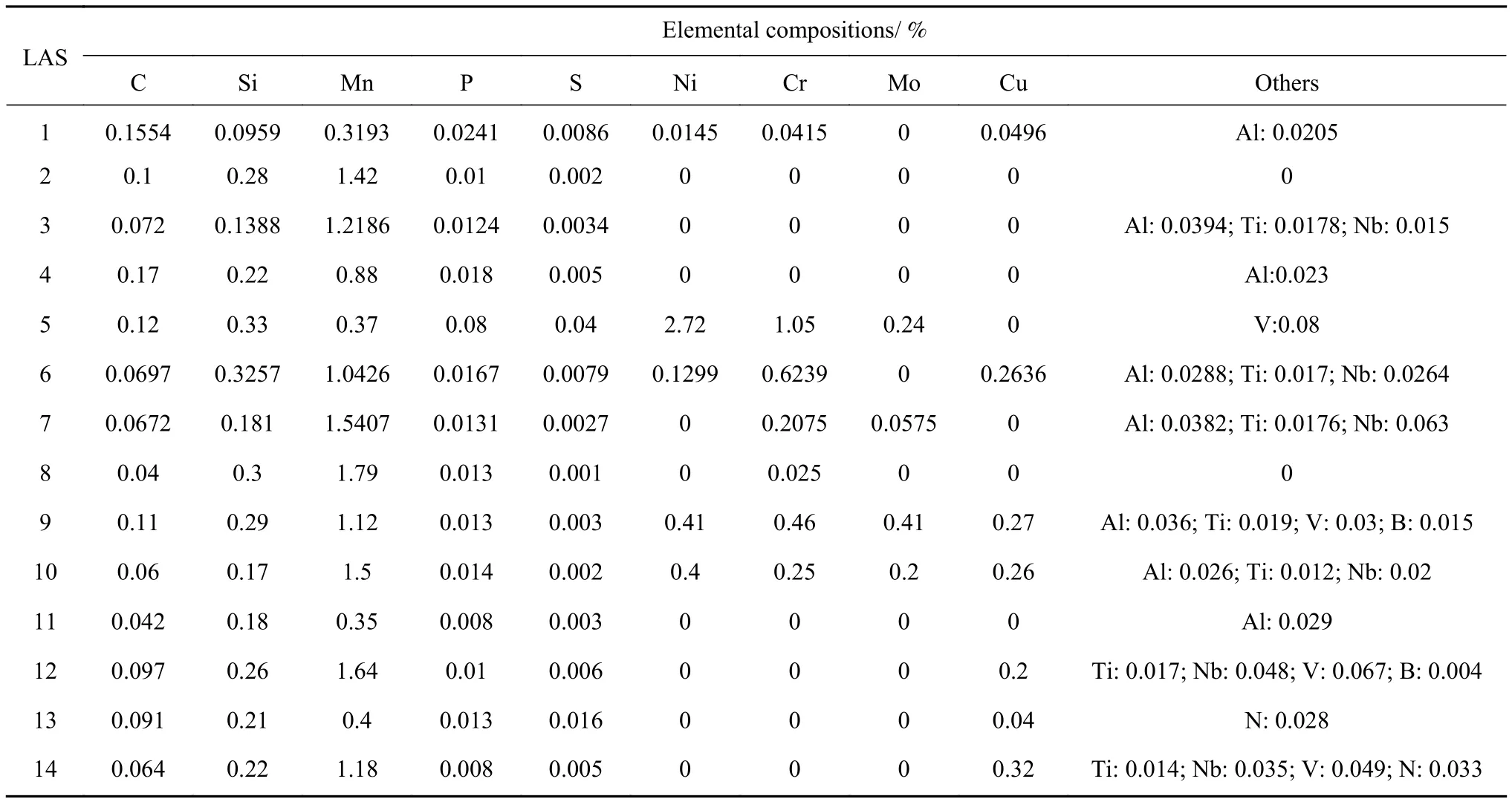
表1 14种低合金钢的化学元素成分(质量分数)Table 1 Elemental compositions of 14 low alloy steels
1.3 腐蚀电位数据
将14种不同的低合金钢试样置于近海低潮位水下约0.5 m处浸泡,同时采用多通道电位自动采集装置[20]对实验钢材的腐蚀电位进行实时监测采集,采样周期为1 h,每种材料各采集到3044条数据,如图1所示.

图1 试样海水腐蚀电位Fig.1 Seawater corrosion potential of test samples
1.4 海水环境数据
海水环境因子包括海水温度(T/℃)、海水电导率 (G/(μS·cm−1))、海水溶氧量 (DO/(mg·L−1))、海水pH、海水盐度(S/%)以及海水氧化还原电位(ORP/mV).在浸泡实验开展的过程中,每隔10 d采集一次低合金钢所处的海水环境因子数据,每种环境因子各采集到14条数据,如图2所示.
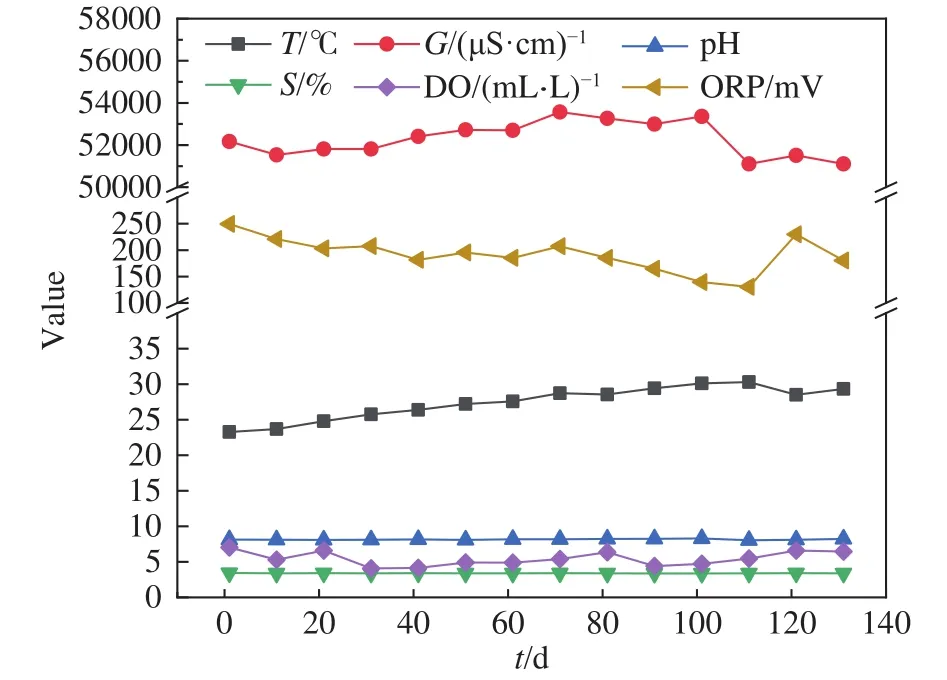
图2 海水环境因子监测值Fig.2 Monitoring values of seawater environmental factors
2 算法分析
2.1 天牛须搜索算法
天牛须搜索[21](Beetle antennae search, BAS)算法是2017年提出的一种高效的智能优化算法.BAS算法受天牛觅食原理启发而开发,当天牛觅食时,天牛并不知道食物位置,而是根据食物气味强弱来觅食.如果天牛左边触角接收到的气味强度比右边大,那么下一步天牛向左爬行,否则向右爬行,依据这一简单原理天牛可以有效找到食物.BAS算法无需知晓函数的具体形式和梯度信息,并且仅需要一个搜索个体,其相比于粒子群算法的运算量大大降低.同时,与遗传算法和模拟退火算法相比,BAS算法代码实现简单,避免了遗传算法中复杂的交叉、变异操作,收敛速度更快[22].其算法流程图如图3所示.
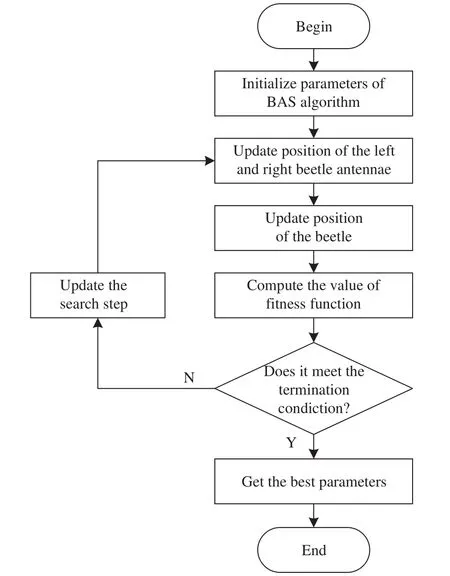
图3 BAS 算法流程图Fig.3 Flowchart of the BAS algorithm
第一步 创建天牛朝向的随机向量且做归一化处理:
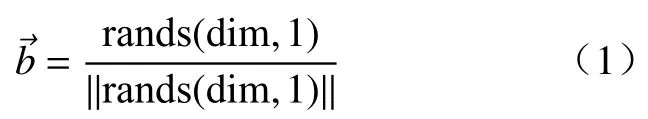
式中,rands()为随机函数,dim表示空间维度.
第二步 创建天牛左右须空间坐标:
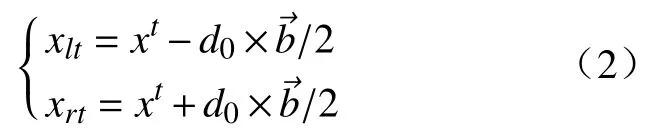
式中,xlt和xrt分别表示天牛左须和右须在第t次迭代时的位置坐标;xt表示天牛在第t次迭代时的质心坐标;d0表示天牛左右须之间的距离.
第三步 根据适应度函数fitness()判断天牛左右须气味强度,即fitness(xlt)和fitness(xrt)的大小,并判断天牛前进方向:
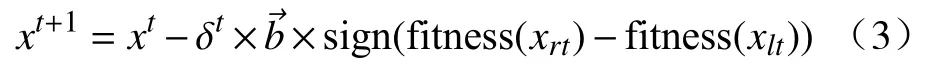
式中,xt+1表示天牛在第t+1次迭代时的质心坐标;δt表示在第t次迭代时的步长因子;sign()表示符号函数.
第四步 计算天牛移动后的适应度函数值并判断是否满足迭代结束条件,若满足迭代结束条件则迭代结束并跳转第六步,否则跳转第五步.
第五步 更新步长因子的值并重复第二步~第四步:

式中,δt+1表示在第t+1次迭代时的步长因子;eta为步长因子的衰减系数,通常将eta取0.95.
第六步 获得最优参数,搜索结束.
2.2 基于CIV的双率腐蚀数据处理方法
由于腐蚀电位和海水环境因子的采样周期各不相同,因此在建立预测模型之前需要对双率腐蚀数据进行预处理.为了克服均值法处理带来的数据信息损失问题,提出了一种基于CIV的双率腐蚀数据处理方法,其具体步骤如下:
第一步 取采样周期为T1的m维(m个海水环境因子)的输入采样数据序列X(kT1)=[x1(kT1),x2(kT1),···,xm(kT1)]T以及采样周期为T2的由p个分量(p种材料)组成的1维输出采样数据序列Y(kT2)=[y1(kT2),y2(kT2),···,yp(kT2)],其中T1远远大于T2,k表示第k条样本.对Y(kT2)采用均值法处理从而将双率数据转换为单率数据 {X(kT1),Y(kT1)},其样本数量显著减少.
第二步 定义综合指标值CIV表征海水输入环境因子对腐蚀电位的综合影响,其定义式如下:
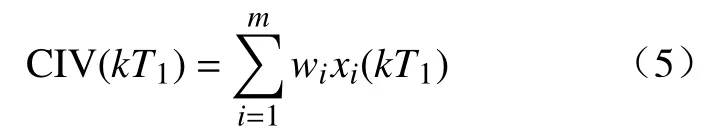
式中,m表示海水环境因子的个数,xi(kT1)表示海水环境因子数据,wi是每个海水环境因子的权重,是待优化参数.
第三步 采用2.1节的BAS算法对上一步中的参数进行寻优.寻优目标设置为:
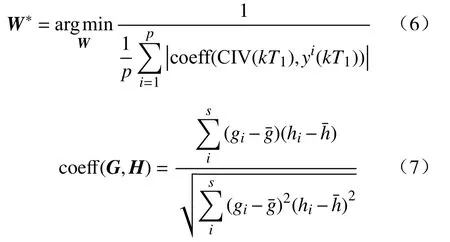
式中,对任意一个参数向量W进行寻优判断,最终可以得到最优的参数向量W*.其中coeff()用于计算任意两个长度相同且均为s的序列的Pearson相关系数,其计算公式由式(7)给出,其中和分别表示序列G和H的均值.|coeff()|越大,两变量的线性相关程度越高.寻优目标意义在于使序列CIV(kT1)与输出中每个分量yi(kT1)的|coeff()|均值最大.
第四步 得到最优参数向量W*后,通过式(5)可以计算得到最优的CIV序列,将其表示为CIV∗(kT1).此时CIV∗(kT1)与输出中每个分量序列yi(kT1)的线性相关程度最大,可以分别建立最小二乘线性回归模型:
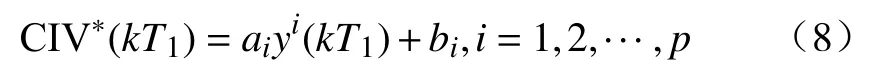
式中,针对p个分量共建立p个最小二乘线性回归模型,ai和bi分别表示第i个模型的斜率和截距.第五步 将原始输出序列分别代入式(8)中对应的最小二乘模型可以计算得到对应的CIV序列CIVi(kT2)(i=1,2,···,p),取其均值为
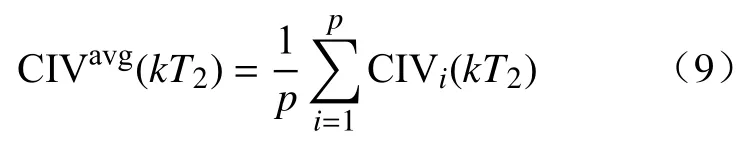
可以将原始的双率采样数据{X(kT1),Y(kT2)}转换为采样周期为T2的单率采样数据 {CIVavg(kT2),Y(kT2)},保留了原始数据更多的信息,获得了更多的建模样本.
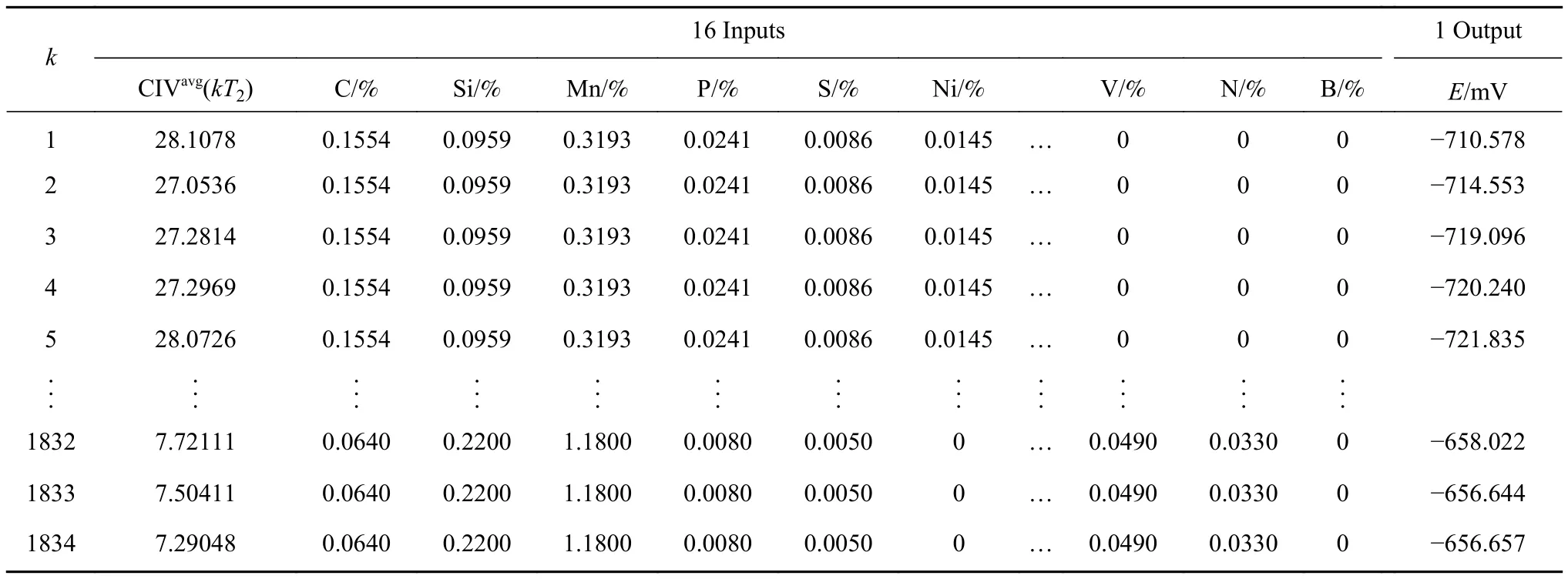
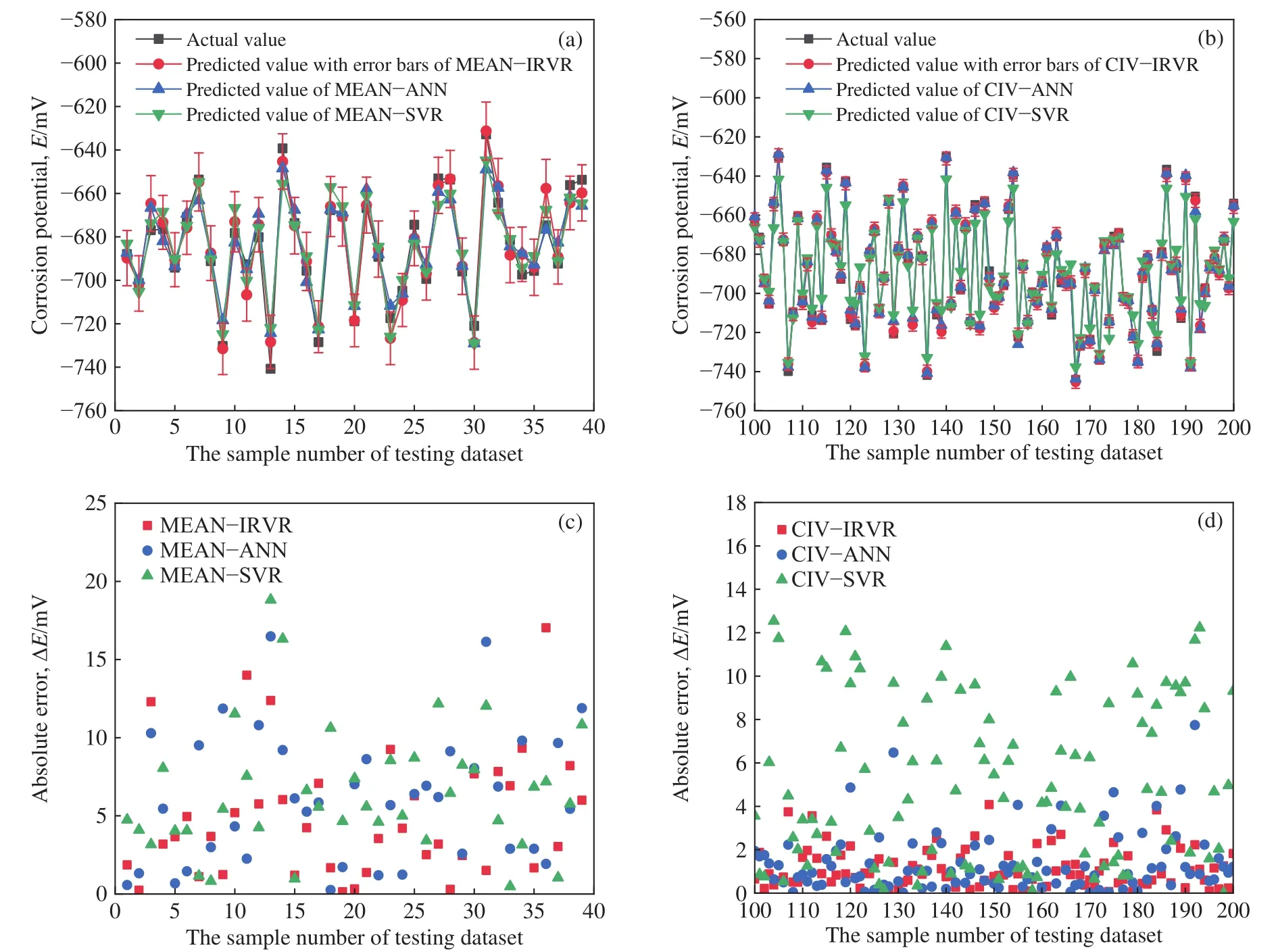
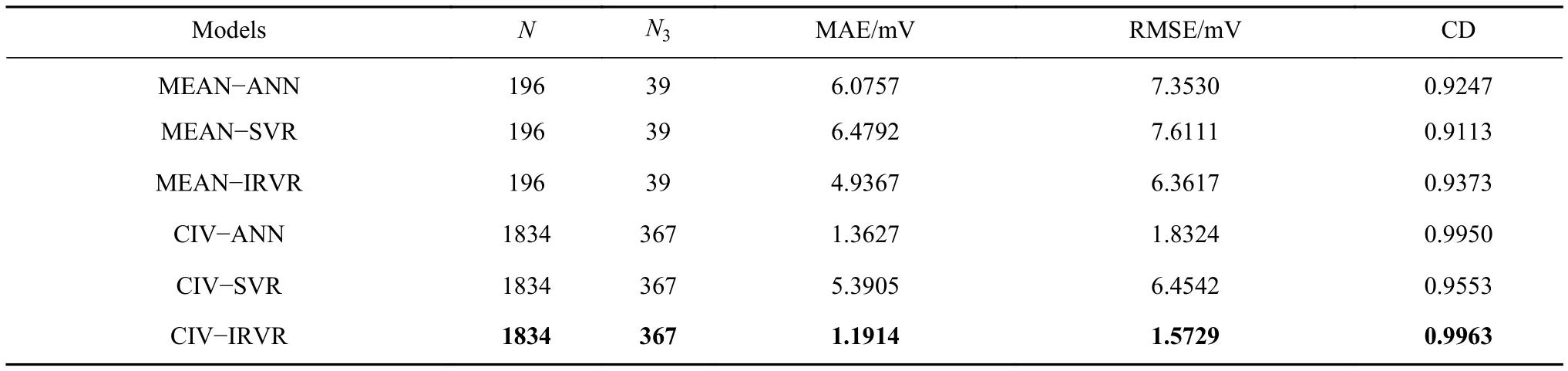
上述流程提出了输入变量采样周期大于输出变量采样周期(T1>T2)情况下的双率数据处理方法.对于输入变量采样周期小于输出变量采样周期(T1 2.3.1 RVR 原理 相关向量回归 (Relevance vector regression, RVR)是由Tipping[23]于2001年提出的一种与SVM类似的监督学习方法.RVR与SVR最大的区别在于:RVR基于贝叶斯理论框架,能够得到具有概率特性的预测结果.同时,RVR的核函数不受MERCER定理(核矩阵必须是连续对称的正定矩阵)限制,可以任意构建核函数[24]. 式中,N是输入输出样本数量;w= [w1,w2, …,wN]T是权值向量;K(x,xi)是核函数;εi是独立均匀分布的零均值高斯噪声.对于各自独立的输出目标oi,输入输出样本数据集的似然估计函数P(oi|w,σ2)可以表示为: 式中,o= [o1,o2.···,oN]T是样本数据集的输出目标向量;w是权值向量;σ2是样本输入的方差;Φ=[φ(x1),φ(x1),···,φ(xN)] 是基于核函数的N×N+1 的矩阵,其中φ(xi) = [1,K(xi,x1),K(xi,x2) , ··· ,K(xi,xN)].为了避免求解式(11)中w和σ2时产生过于拟合的现象,对w赋予先验的条件概率P(w|α),即 上式中,α= [α0,α1,···,αN]T是N+ 1 维的超参数向量.根据贝叶斯公式,所有未知参数的后验概率分布P(w|o,α,σ2)可以表示为: 式中,μ=σ−2ΣΦTo表示权重向量w的均值向量;Σ= (σ−2ΦTΦ+A)−1表示权重向量w的后验协方差矩阵,其中A= diag(α0,α1,···,αN).此外,计算超参数向量α以及方差σ2的公式为: 式中,μi表示均值向量μ的第i个元素;γi= 1 –αiΣii,其中Σii表示后验协方差矩阵Σ中的第i个对角线元素.对于给定的新输入变量值x*,根据式(14)和式(15)可以求解出对应的超参数 αMP和方差,其对应输出o*的概率分布服从高斯分布,其可以表示如式(16)所示: 其中预测均值y*和方差σ*可以分别表示为: 上式中,y*表示输入x*对应的RVR模型预测均值;方差σ*可用于表征RVR预测结果的置信区间,例如RVR预测结果的95%的置信区间可以表示为. 2.3.2 IRVR 方法 在RVR模型的核函数中,一般采用单一核函数,比如高斯核或多项式核.高斯核是典型的局部核,而多项式核是典型的全局核[25].为了兼具局部核与全局核的优势,选择将高斯核与二次多项式核进行组合实现IRVR方法[26],组合核函数如下所示: 式中,组合核函数由高斯核和二次多项式核构成.xi和yj表示数据空间中的样本点,λ1和λ2是核参数,α和β分别是核函数对应的权重参数.因此RVR核函数的待优化参数向量可以表示为V= [λ1,λ2,α,β],采用 BAS 算法可以对参数向量V进行寻优. 将CIV方法与IRVR方法结合构建海水腐蚀双率数据的CIV−IRVR预测模型.基于CIV方法得到的均匀单率腐蚀数据 {CIVavg(kT2),Y(kT2)}以及低合金钢的化学元素成分,将CIV序列和化学元素设置为模型输入,腐蚀电位数据设置为输出,构建海水腐蚀电位的预测模型,其表达式如式(20)所示: 式中,N是样本总数;Y(kT2)和 CIVavg(kT2)分别表示第k条样本中的腐蚀电位数据和综合指标值数据;e1,e2,···,en表示低合金钢的n种化学元素成分含量. 采用平均绝对误差 (Mean absolute error, MAE)、均方根误差 (Root mean square error, RMSE)以及决定系数 (Coefficient of determination, CD)评价模型的泛化性能,其计算公式如下: 其中,ypred(i)和ytrue(i)分别是第i条样本数据的模型预测值和真实值,true(i)表示所有真实值的均值.当MAE、RMSE越小时,模型的预测误差越低;当CD越接近1时,模型的拟合能力越强,预测性能越好. 由图2易知,在六种海水环境因子中海水pH和海水盐度(S/%)监测值的变化幅度非常小,对低合金钢的海水腐蚀电位影响甚微,因此在构建海水腐蚀数据集时选取变化显著的包括海水温度 (T/℃)、海水电导率 (G/(μS·cm−1))、海水溶氧量(DO/(mg·L−1))以及海水氧化还原电位 (ORP/mV)的四种海水环境因子.采用CIV方法对双率腐蚀数据进行处理,经BAS算法寻优得到的最优CIV参数向量的结果为W∗=[−4.0193,0.002962,−2.2203,−0.060905],进一步将双率数据转化为单率数据,并构建用于建模的数据集.如表2所示,经CIV方法处理得到的海水腐蚀数据集包含16维输入变量以及1维输出变量,共计1834条数据. 表2 经CIV方法处理得到的海水腐蚀数据集Table 2 Seawater corrosion dataset obtained via the CIV method 将表2所示的海水腐蚀数据集(样本总数N=1834)按 6∶2∶2 随机划分为训练集(样本数N1=1100)、验证集(样本数N2= 367)和测试集(样本数N3= 367).在训练集上对模型进行训练,在验证集上对IRVR组合核函数的参数向量V进行寻优,最终在测试集上计算模型的各项评价指标值以实现对模型预测能力的评估. IRVR模型组合核函数的参数向量V由随机函数生成.BAS算法中,最大迭代次数MAXiter=50,天牛左右须初始距离d0= 0.2,初始步长因子δ0=1,衰减系数 eta = 0.95,其适应度函数设置为模型在验证集上的RMSE,寻优目标为使验证集上的RMSE最小,即 式中,V*为最优参数,N2为验证集样本数量,ypred(i)和ytrue(i)分别是验证集中第i条样本的预测值和真实值. BAS寻 优 得V∗=[0.25697,0.53225,1.3585,−0.26342],采用最优组合核函数参数V*构建的CIV−IRVR模型计算测试集上的三种评价指标值,并将其结果与均值法结合IRVR、BP和SVR建立的MEAN−IRVR、MEAN−ANN 和MEAN−SVR模型以及本文CIV方法结合BP方法和SVR方法建立的模型CIV−ANN和CIV−SVR进行比较. 3.4.1 预测结果对比 为了评估CIV−IRVR模型的性能,使用图4来比较不同预测模型的预测结果. 图4(a)展示了基于均值法方法建立的MEAN−ANN、MEAN−SVR以及MEAN−IRVR模型在测试集上的结果;图4(b)展示了基于CIV方法建立的CIV−ANN、CIV−SVR以及CIV−IRVR在部分测试集上的预测结果;图4(c)和图4(d)分别展现了基于MEAN和CIV方法建立的预测模型在测试集上绝对误差的分布.可以直观看出当数据处理方法由MEAN方法转变为CIV方法后,模型预测精度有了大幅提高,采用IRVR方法建立的模型相比于BP和SVR能够得到带有误差棒的预测输出,同时CIV−IRVR模型在测试集上的绝对误差分布离0值最近,其建模预测结果最为理想. 图4 不同模型在测试集上的预测结果及绝对误差.(a)基于MEAN的三种模型;(b)基于CIV的三种模型;(c)基于MEAN的三种模型的绝对误差值;(d)基于CIV的三种模型的绝对误差值Fig.4 Prediction results and absolute errors of different models: (a) three models based on the MEAN method; (b) three models based on the CIV method; (c) absolute errors of the three models based on the MEAN method; (d) absolute errors of the three models based on the CIV method 3.4.2 评价指标对比 列出上述四种双率腐蚀数据处理和建模方法的样本数量N和测试集样本数量N3并计算预测模型在测试集上的评价指标值,如表3所示. 表3 不同模型的样本数量和预测误差表Table 3 Sample size and prediction errors of different models 从表3可以看出,相比于均值方法处理双率腐蚀数据得到的196条建模样本,通过CIV方法得到的建模样本数量为1834,表明CIV方法处理双率腐蚀数据能够更多地保留原始数据中的信息,从而减少信息损失.在预测指标上,CIV−IRVR模型的 MAE、RMSE和 CD分别为 1.1914 mV、1.5729 mV及0.9963,与其他预测模型相比,具有最小的预测误差和最高的决定系数.与用均值法处理双率数据后同样结合IRVR方法建立的MEAN−IRVR模型相比,CIV−IRVR模型的MAE和RMSE分别降低了 3.7453 mV 和 4.7888 mV,CD 提升了 0.0590,进一步表明CIV方法相比于均值法保留足够数据信息并获得更多建模样本在预测精度上的优势.相比于CIV方法建立的CIV−ANN以及CIV−SVR预测模型,CIV−IRVR在MAE、RMSE以及CD指标上均取得了最优效果,凸显了优化IRVR方法建立的模型在预测精度上的优势.通过以上分析,基于CIV方法结合IRVR方法建立CIV−IRVR模型不仅能够减少数据信息损失还具有很高的建模精度,对于海水腐蚀双率数据的处理和建模是十分有效的. (1)提出了一种基于CIV的双率数据处理方法,通过构建CIV表征海水环境因子对腐蚀电位的综合影响,建立CIV与腐蚀电位的关系模型将低合金钢海水腐蚀监测中的双率数据转化为单率数据用于建模,减少了原始数据的信息损失. (2)通过BAS优化组合核函数参数的IRVR方法对CIV方法处理得到的腐蚀数据集进行建模,得到了低合金钢海水腐蚀电位预测模型CIV−IRVR,并与包括均值法建立的MEAN−ANN、MEAN−SVR和MEAN−IRVR、CIV方法结合ANN和SVR建立的CIV−ANN和CIV−SVR进行对比.实验表明,CIV−IRVR在MAE和RMSE两项误差指标上达到了最低,在CD指标上达到了最高,获得了最佳的预测效果. (3)CIV−IRVR在保留更多数据信息的同时还具备较高的预测精度,能够很好地解决海水腐蚀中双率数据的处理和建模问题,对于材料腐蚀状态的预测及进一步指导腐蚀防护工作有一定的参考价值和现实意义.2.3 IRVR方法
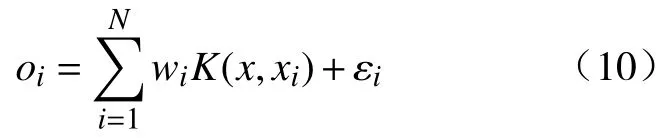
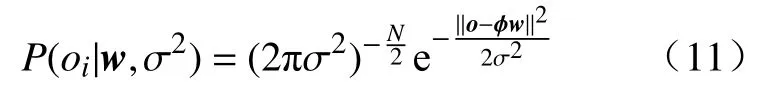
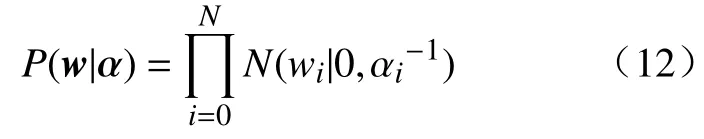
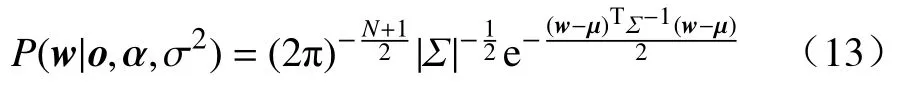
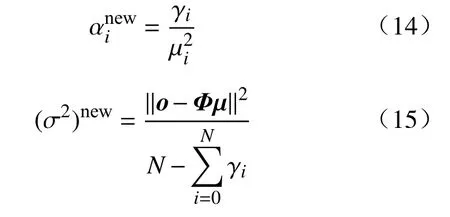
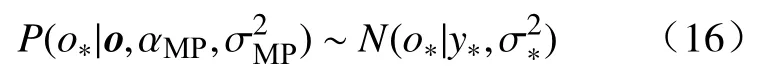
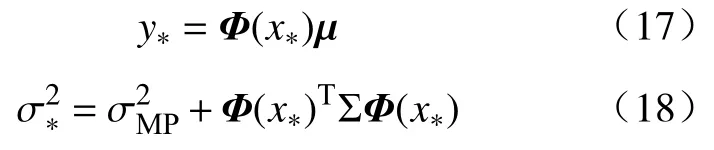
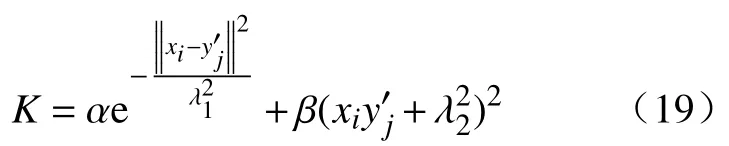
2.4 CIV−IRVR模型
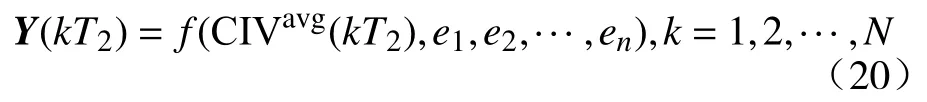
3 实验结果及其讨论
3.1 评价指标
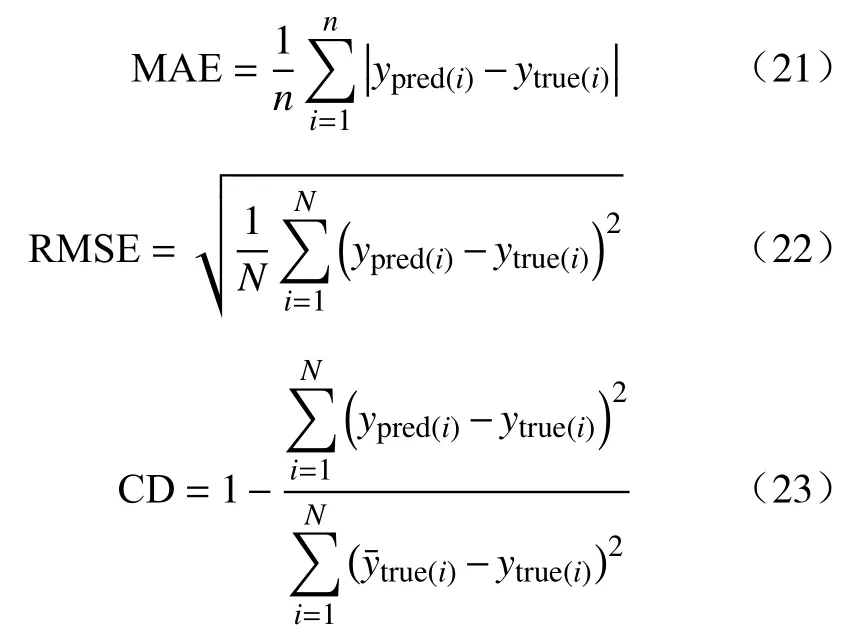
3.2 海水腐蚀数据集
3.3 CIV−IRVR模型训练
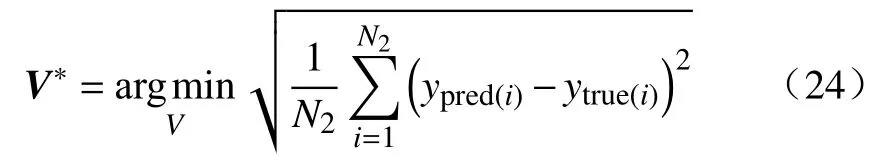
3.4 CIV−IRVR模型训练
4 结论

