一道数学竞赛试题的修正与思考
楼思远, 金 熠
(杭州第十四中学,浙江 杭州 321006)
近日,笔者在解答2021年浙江省数学竞赛试题第9题时发现题中所给的三角形并不存在,在给出证明之后对题干进行了修正,给出了几种不同的解题方法,并进行了变式探究.
1 试题修正

(2021年浙江省数学竞赛试题第9题)
实际上,当点P,Q分别在线段AC,BC上运动时,
(1)
其中
因此本题有误,分析如下:
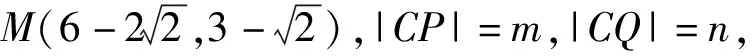
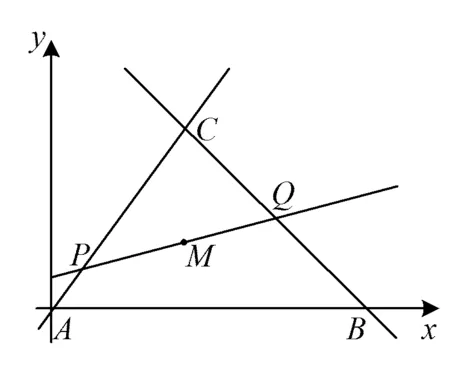
图1
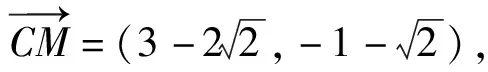
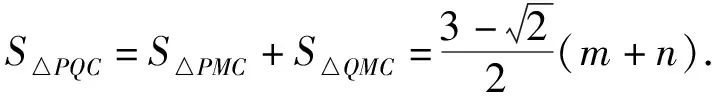
(2)
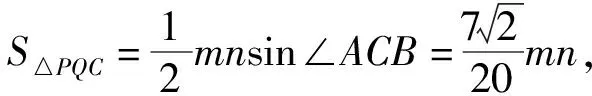
(3)
结合式(2)和式(3),消去m,得
(4)
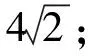
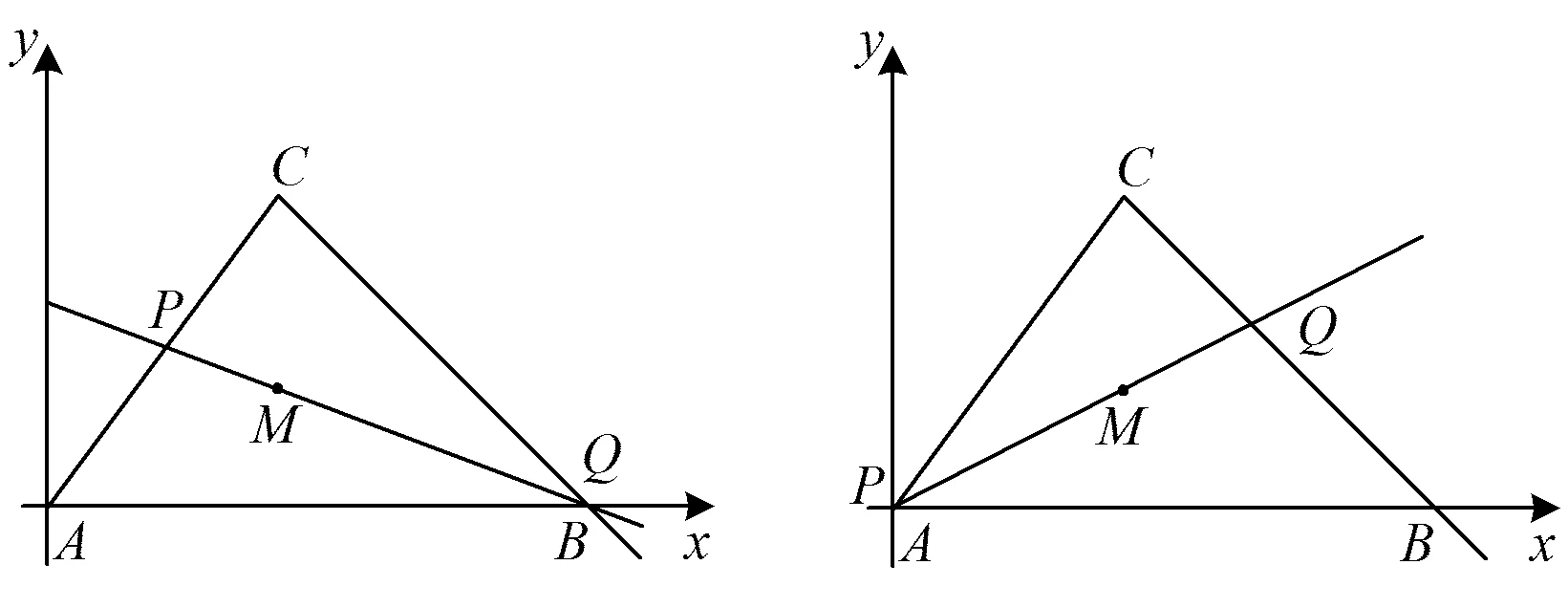
图2 图3
根据上述计算过程,结合图2和图3可知
(S△PQC)max=max{S△PBC,S△AQC}.
对于S△PQC的最小值,从基本不等式入手更为简洁:

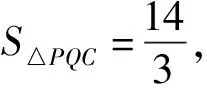
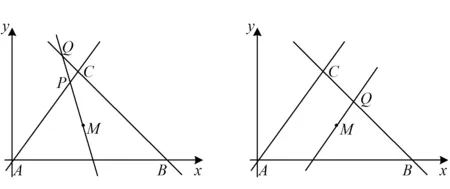
图4 图5

解法1(向量面积公式)以图4为例,仿照前面的思路知

(5)
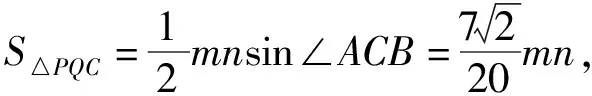
(6)
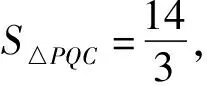
即
评注涉及三角形面积相关问题时,运用向量面积公式往往能让过程简洁而巧妙,在求得关于m,n的等量关系后,利用设而不求的思想,通过整体代换解得结果.
2 解法拓展
本题是一道起点低、入口宽、立意高的好题.下面就该题的不同思考角度,再给出几种解法,以期抛砖引玉(以下解法仍然以图4为例).
解法2(三点共线性质)根据点Q,P,M共线可知:存在实数t,使得
将各点的坐标代入,得
即
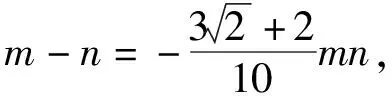
后同解法1.
评注向量三点共线公式是课本中一个重要结论,无论是针对高考或是竞赛,都需熟练掌握.根据题目条件,结合图像特点,选择三点共线公式让解题过程显得自然而高效.
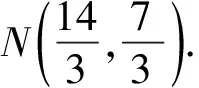
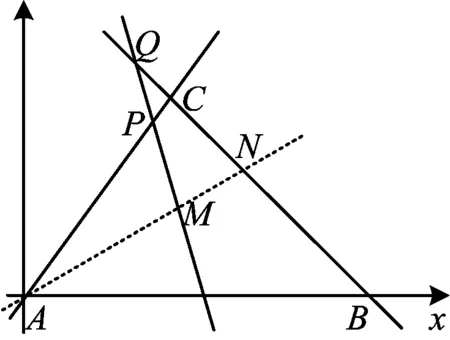
图6
即
整理得
后同解法1.
评注三角函数是连接代数与几何的桥梁之一,在处理某些三角函数问题时,若能运用一些著名的几何定理,则可以避开繁复的代数运算,快速求得结果.
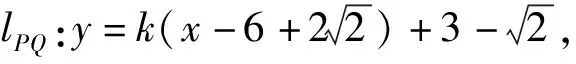
知
同理可得
由弦长公式得
同理可得
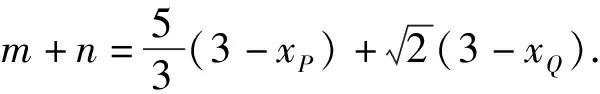
(7)
(3-xP)(3-xQ)=4,
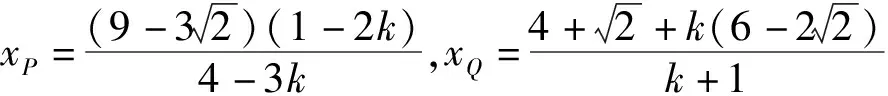
评注根据题中所给的条件和结构,联想并建立相应的解析几何模型,把代数问题几何化,借助解析几何的有关知识问题,使解题过程水到渠成.
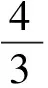
进而可以得到式(5),后同解法1.
实际上,根据三角形内心I的坐标公式(在△ABC中,设A(x1,y1),B(x2,y2),C(x3,y3),a=|BC|,b=|CA|,c=|AB|),得
可知点M即为△ABC的内心.
评注解法5是最简洁的,从中可看出点M的由来.但该解法要求解题者对内心坐标公式熟记于心,或者具备敏锐的直觉与观察力,因此解法5的运用范围有限.
3 变式探究
解题艺术的精髓在于对各类解法的关键点、价值点进行回顾与总结,并通过各种变式来加深对于问题的理解.笔者尝试编拟了以下3个变式练习,以期提升对原题的感悟与欣赏.


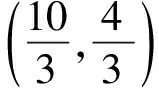
上述3个变式的解答过程与结果留给读者完成.
4 总结思考
拿到一个数学问题,不仅要关注其解题过程与结果,更需进行题后反思,如审视解题过程有无漏洞、步骤是否可以简化、答案是否合理(存在)等.在此基础之上,可以对原题展开多解研究,通过对问题多角度思考、多方法求解,充分掌握知识的各个层面及交汇知识的综合与应用.更进一步,可以对原题进行变式探究(练习),其思路包括:从本题的条件出发还能得到其他结论吗?本题的逆命题是否仍然成立?本题的解法可以推广到一般吗?诸如此类的多层次变式探究,可以帮助寻找到解决问题的“关键点”乃至命题人的思路,从而达到“既见树木又见树林,将数学思维水平抽象与升华”的目的.

