基于数学建模的恰当问题引导——以“反比例函数应用”第一课时为例

沈顺良, 沈凯明

(1.海盐县教育研究中心,浙江 海盐 314399;2.通元中学，浙江 海盐 314399)

数学建模是对现实问题进行数学抽象、用数学语言表达问题、用数学方法构建模型解决问题的素养.在日常教学中，各类新知学习后的应用问题解决，是发展数学建模的良好时机，课内教师的恰当问题引导，是发展数学建模的重要策略.下面以“反比例函数应用”第一课时为例加以呈现和分析.

1 情景问题引导，从数学的视角发现和提出问题

教师抛出问题1.

问题1高老师开车从新塍镇中学来到美丽的东湖中学，导航地图显示两校相距54 km.如果老师开车的平均速度是60 km/h，那么老师在路上花费多少时间？

生1：54÷60=0.9(h).

师：你是利用了哪个等量关系？

生1：因为“速度×时间=路程”，所以“时间=路程/速度”.

师：如果汽车的平均速度是vkm/h，那么汽车行驶多少小时到东湖中学？

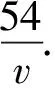
师：上述情景中可以抽象出怎样的数学关系？依据是什么？

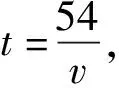
分析与思考本教学片段以教师开车来学校的行程问题作为情景，从特殊到一般，将具体化的速度和时间分别抽象成v和t，再通过“利用了什么等量关系”“抽象出怎样的数学关系”及其依据等问题，引导学生从数学的视角发现并提出现实中的数学问题，整个过程通过问题的自然发现和提出，既提升了学生分析问题的能力，又为下一环节的求解模型奠定基础.

2 变式问题引导，经历分析和构建模型的过程

变式1高老师开车来学校，要求在8时40分前报到.

1)若车速不超过90 km/h，则高老师最晚几点出发？

2)若有雾车速不超过50 km/h，则高老师最晚又是几点出发？

师：这里已知报到时间，需要求什么？通过什么去求？

生3：求出在速度限制的上限下所需要的时间，根据已知的路程和所限的速度来求.

师：具体怎么求？

师：如何求解变式1中的问题1)和问题2)？

生3：两个问题中的速度分别不超过90 km/h和50 km/h，就是所需时间分别要不小于0.6 h和1.08 h了，然后再按照8时40分往前算.

师：你能从函数角度来分析解决吗？

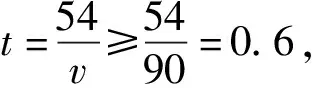
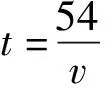
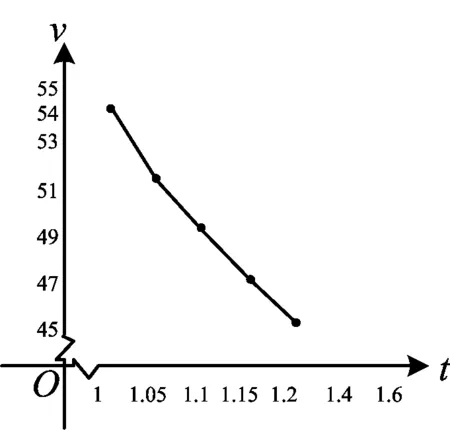
图1

师：请你回顾上述问题的分析与解决过程.

生6：由问题中条件和所求找到速度与时间的关系，在数学化后利用反比例函数的式子运算求解，或利用其图像直观理解，从图像中可直观看到增减情况.

分析与思考首先是提出问题“需要求什么、通过什么求、具体怎么求”，引导学生分析现实速度限制下的时间要求，转化为路程、速度与时间的等量关系，然后是“从函数的角度分析解决”引导学生通过数学运算加以解决，学生自然能够利用反比例函数模型来思考分析.后面的过程则引导学生分析与整理，先确定变量后找等量关系，通过等量关系构建相应的数学模型，利用函数工具来分析，为下一环节的数学模型求解奠定方法基础.

3 不同解法引导，用数学知识求解模型并验证

变式2两校相距54 km，当开车时间要求在1 h和1.2 h之间(不包括1 h和1.2 h)时，开车速度应在哪个范围？

师：找到了数学模型，变式2就是该函数当1

师：将“已知自变量范围求函数值范围”转化为“求不等式的解”.

师：为什么可以求两端的值？

生8：反比例函数在第一象限是递减的.

师：这与实际意义相符吗？

生8：符合的，时间越短则速度越快.

师：解决过程中可以将数学与实际相结合，还有其他方法吗？

生9：可以借助函数图像，当t=1时，v=54；当t=1.2时，v=45，由图1直观可得45

师：你能归纳一下变式2的解决方法吗？

生10：实际问题转化为相应的数学模型后，就可以利用函数工具加以解决，将函数变形为方程、不等式，或利用图像，求解的过程和结果可以用现实意义来加以辅助和检验.

分析与思考教师的提问“找到数学模型后怎么求”，引导学生用不同的方法求解，其中有将函数转化为不等式或方程的化归，也有利用图像的直观想象；通过“与实际意义相符吗”引导学生求解过程中可以用实际意义来辅助理解和检验；最后的问题“能否对变式2作归纳”，让学生回顾小结，建模后求解时可以将模型进行变形，也需要用现实意义检验结果.

4 整体解决过程引导，经历数学建模的全过程

给出如下问题，先独立阅读思考再小组合作：

问题2在温度不变的条件下，通过一次次地对汽缸顶部的活塞加压测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强如表1所示.当压力表读出的压强为72 kPa时，汽缸内气体的体积压缩到多少mL？

表1 缸内气体的体积和对汽缸壁所产生的压强

生11：本题蕴涵着压强P(kPa)与体积V(mL)的关系(如表1所示)，需要找到P和V的一般关系，再依据函数模型来求解.

师：它是什么函数？又如何确立呢？

生11：从表1中看不出，我是将数对放在坐标系下进行直观估计的.如图2，可能是直线，也可能是反比例函数的双曲线.

图2

师：哪类函数更合适呢？

生12：我认为是一次函数.将(100,60)，(90,67)代入P=kV+b，求得P=-0.7V+130.

生14：当P=72 kPa时，代入求得V≈83.33 mL，也就是当压力表读出的压强为72 kPa时，汽缸内气体的体积压缩到83.33 mL.从表1和图2来看都是符合的.

师：回顾整个解题过程，你经历了哪些步骤？

生15：先收集、分析表格中的数据，再用描点法画出图像，接着估计函数的类型，用待定系数法求函数关系式.

教师规范和引导数学建模的一般过程并板书.

分析与思考一是根据题中表格和所求信息，从数学角度发现蕴涵的两个变量之间的一般函数关系;二是用数学的方法即借助几个特殊点画图，先估计函数模型，再加以验证确认，从而构建正确的函数模型;三是利用函数模型求解，并用实际信息加以修正和验证.“如何思考”是引导学生从数学角度去阅读分析，“是什么函数，如何确立”则是引导学生用数学方法由特殊到一般去构建模型，“哪类函数更合适”是引导学生利用实际信息改进和修正模型，“怎么求解、是否正确”是引导学生进行数学求解和实际验证，“经历了哪些步骤”则是指向数学建模解题的全过程.

5 基于数学建模的一般问题思考

数学建模过程主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题[1].数学建模的发展主要依靠日常教学的积累，需要适合的数学素材进行教学，通过恰当的引导性问题，让学生深度经历数学建模的各个过程.

1)在学习各类新知后，精选合适的实际情境问题，引导学生在情境中发现并提出数学问题[2].如本课时中,教师结合自己的上班路途情境，通过不同角度的设问，让学生发现距离一定的情形下时间与速度的关系，从而提出两个变量之间的关系问题.

2)运用数学的知识和原理对现实问题进行数学抽象，用数学语言表达数学问题，建立相应的数学模型[3].本课例中两个变量的反比例关系，通过问题的变式引导，无论从解析式的符号语言形式，还是从图像的几何语言形式，都是将原路程问题抽象并用数学语言表示，然后建立反比例函数的模型.

3)用数学方法解决模型问题.对于已经获得的反比例函数模型，教师引导学生用不同的数学方法加以解决，本课例中有解不等式的方法，也有根据增减性转化为解方程的问题，更有利用图形辅助直观得解.

4)将求得的结果回到实际问题中加以检验，得到正确的结果.这样的检验可以在问题解决的最后结果中，也可以在中间过程的阶段性结论中.在最后的应用问题解决中，模拟函数的确认就是经历了猜想后再检验、确认是否符合实际意义.

在上述教学过程中，教师利用恰当的问题引导师生和生生进行交流、反思、归纳、评价及拓展，值得一线教师学习.