考虑飞机轮挡事件相关时间的航班时刻优化
刘田野,翟文鹏
(中国民航大学空中交通管理学院,天津 300300)
近年来,随着经济与技术的飞速发展我国民航业呈现出一片繁荣景象。据《2019年民航行业发展统计公报》公示,2015—2019年中国民航运输机场旅客吞吐量逐年稳步上升,其中2019年旅客吞吐量达到13.52亿人次,巨幅数字下需要完善的运作系统以保障整个行业顺利运行。由于有限的空中交通流量管理水平,航班延误现象时有发生。从民航局对航空运输消费者投诉情况通报数据得知,在15类投诉问题中航班问题类投诉是每年旅客投诉最多的问题。例如,2018年全年关于航班问题类投诉量多达6 653件,占比总投诉量39.38%,居首位;且该类中航班延误和取消投诉量高达5 787件,占比航班问题类投诉量87%。
在这样的背景下,提升空中交通流量管理技术就显得愈发重要。近年来,越来越多的学者开始对航班时刻问题进行研究。叶博嘉等[1]综合考虑多个目标,建立以总延误时间最少、总延误成本最低、总调整航班架次最少、总延误航班架次最少的多目标、多机场地面等待问题模型。杨尚文[2]对机场不确定型容量问题进行研究,对不确定容量条件下的地面等待问题和协同时隙分配问题分别建立了静态和动态模型。Aloulou等[3]提出了一个全新的考虑飞机和乘客连接的具有鲁棒性航班时刻优化模型。彭瑛等[4]将航班时刻和跑道容量结合起来,把平均跑道延误时间加入目标函数。田勇等[5]提出了基于市场机制的地面等待时隙分配方法,模型中纳入了动态时隙市场价格。Jacquillat等[6]提出了一种综合优化方法,该方法可在战略层面上对机场的航班时刻表进行优化,在战术层面上对机场的容量利用率进行优化。杨新湦等[7]在考虑进离港航班相互关系的基础上进一步加入了旅客最小中转时间约束,使模型优化更精进一步。齐莉[8]通过对枢纽机场航班波的研究,约束中同样加入了最小旅客中转时间需求,最终通过削峰填谷的形式优化航班时刻。王倩等[9]从时间和空间两个维度引入排队论原理,将机场群航班的进离港看作是不同的排队系统并建立双层优化目标对珠三角机场群航班时刻进行优化。张兆宁等[10]建立了航班延误传播模型,对源机场和目的机场前后序以及前后行两种延误传播均建立了相应的延误传播概率并通过实例验证了模型的有效性。周语等[11]针对大面积航班延误恢复问题考虑了不确定性因素的影响,模型在兼顾航空公司公平性的同时提高了恢复计划的鲁棒性。汪梦蝶等[12]重点从航班时刻可接受调整量水平的角度进行考虑,通过最小化超过可接受调整量的数量实现可接受性目标。王兴隆等[13]将易感者-染病者-易感者(susceptible-infective-susceptible,SIS)传染病模型应用到机场网络延误传播。Jane等[14]针对航班已经出现和将要出现扰动的两种情况,提出了一种措施补救性和主动预防性的方法,该方法可减少航班延误的预期恢复成本。柯雨辰等[15]将机位、跑道以及走廊口作为一个系统进行研究,通过对三个方面的容量进行约束建立了更加面向实际运行的优化模型。
综上,航班时刻优化研究不断深入,大致可分为三类:延误预防、延误预测以及延误恢复。众多模型以航班时刻调整量、机场延传播误、相关容量约束等为突破点进行研究,但现有研究中关于航班轮挡时间的研究较少。基于“航班时刻表”的管理模式在我国实际运行中占据主导地位,近些年由于航班量大幅增长及在实际运行中其他各种未知因素的影响,这种管理模中的弊端逐渐凸显。但是通过对航班实际运行进行科学的统计分析可以优化空中交通问题[16]。为此,着力于提高航班准点率、减少航班上轮挡及撤轮挡的延误,首次对航班撤轮挡时间和轮档时间两个与轮挡事件相关的时间量进行研究,并首次将泰尔指数作为航班时刻优化研究领域的公平性目标函数。模型中建立了概率型约束条件,针对模型求解引进了增加种群多样性的粒子群算法以提高求解质量。最后,以杭州萧山国际机场为算例验证模型的有效性。
1 模型介绍
1.1 相关概念
1.1.1 轮挡时间
飞机滑行停稳后,在机轮下放置轮挡防止飞机运动。当飞机启动发动机准备运动时地面人员撤去轮挡,该时间点为撤轮挡时间。从此时起计算飞机着陆再次放置轮挡的一段时间称为轮挡时间。飞机由于某些原因(如天气、流量管控等)未能在规定的时间准时完成轮挡,其完成时间呈现出随机性。
1.1.2 连续航班
具有某些相同资源的航班。例如:乘客、飞机或机组人员。连续航班是指在进离场前后共用一架飞机的航班,图1所示的航班i和航班j为连续航班。由于航班i和航班j由同一架飞机执飞,故航班i的进港状态会直接影响到航班i的离港状态。

图1 连续航班Fig.1 Consecutive flights
1.1.3 最少过站时间
航班最少过站时间指对应某种机型计划过站需要的最少时间,根据民航局制定的《民航航班正常统计办法》,中国繁忙机场机型最少过站时间要求如表1所示。

表1 机型最少过站时间Table 1 The minimum transit time of models
1.1.4 松弛时间
松弛时间即飞机过站时间减去最少过站时间所余下的时间。当上游航班延误时,该部分时间可起到削减上下游航班之间的延误传播的作用,松弛时间如图2所示。

图2 松弛时间示意图Fig.2 Schematic diagram of relaxation time
1.2 轮挡相关时间
所研究的轮挡相关时间是指与轮挡事件相关的两个阶段时间,两个阶段如图3所示。其中第一阶段为撤轮挡时间,此时间量为一个时间点。航班可能受流量管控或地勤服务等原因的影响从而导致完成撤轮挡的时间出现提前、准时或延迟的情况。第二阶段为轮挡时间,此时间量具有时间长度。由于航班到下一机场上轮挡之前一直处于运动状态,过程中存在较多不确定性因素,飞机可能会受到天气、速度等原因的影响从而导致飞机实际轮挡时间出现波动变化的情况。

图3 两阶段随机时间示意图Fig.3 Schematic diagram of two-stage random time
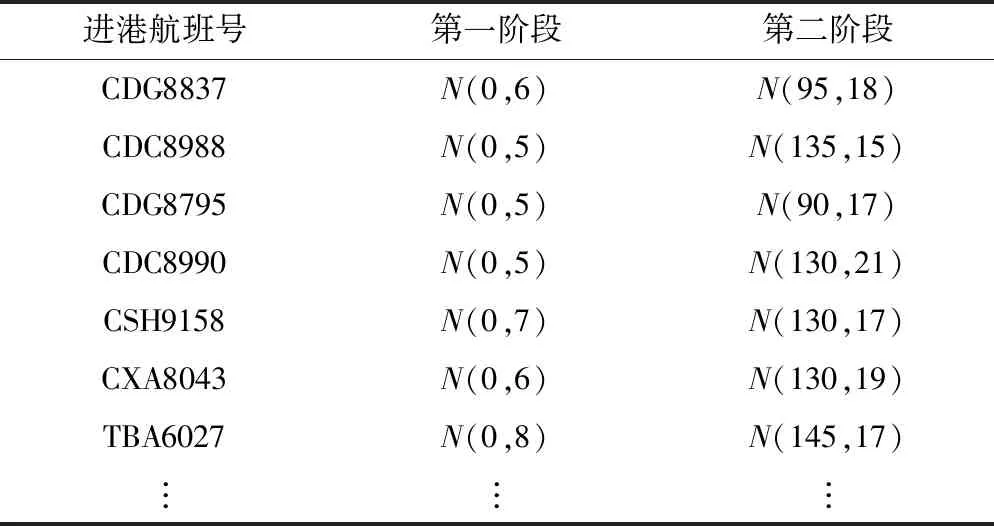
从随机性的角度考虑两个时间量,其概率分布需在大量样本统计的基础上进行计算,由于统计数据涉及到大量航班在上游机场开始运行时的大量历史数据,精确表示确有一定难度,对其进行合理假设有助于求解且不失一般性。正态分布具有良好的性质,设两个阶段的时间符合正态分布。由于撤轮挡时间为一个时间点不具有时间长度,可设均值为零以方便个后续计算,方差可由实际撤轮挡时间与计划撤轮挡时间的差进行计算求得。对于轮挡时间其均值表示计划轮挡时间长度,方差由实际轮挡时间长度与计划轮挡时间长度的差进行计算求得[17]。
根据假设2以及独立正态分布随机函数的性质,可将第一段和第二段的概率密度分布进行累加从而将两阶段合为一个阶段,简化运算,如:某航班撤轮挡时间分布为N(0,6),轮挡时间分布为N(120,25),故累加后整个过程将符合分布N(120,31)。
1.3 模型假设
假设1所有航空公司的航班时刻最大调整量相同。
假设2飞机撤轮挡时间与轮挡时间相互独立互不无影响。
假设3飞机撤轮挡时间和离港时间相等,上轮挡时间和进港时间相等。
假设4机场航班进离港不受影响。
1.4 符号定义
模型中所用符号定义如表2所示。

表2 符号定义Table 2 Symbol definition
1.5 目标函数
以航班时刻最大调整量最小作为效率目标函数;同时考虑到时刻调整的公平性问题,本文首次使用泰尔指数作为公平性目标函数。泰尔指数原本用于反映不同国家或地区之间收入差距的经济性指标,其值越小表示区域间差异越小,将其延伸到航班时刻调整量方面。
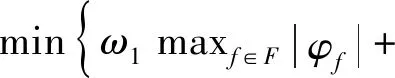
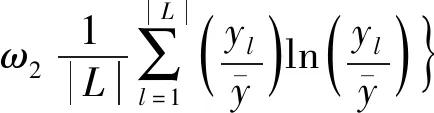
(1)
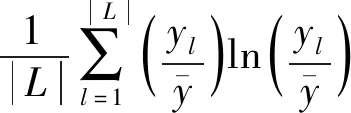
1.6 约束方程
(1)时刻分配唯一性约束:
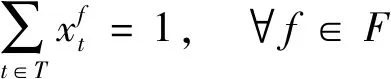
(2)
(2)机场容量约束:
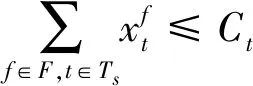
(3)
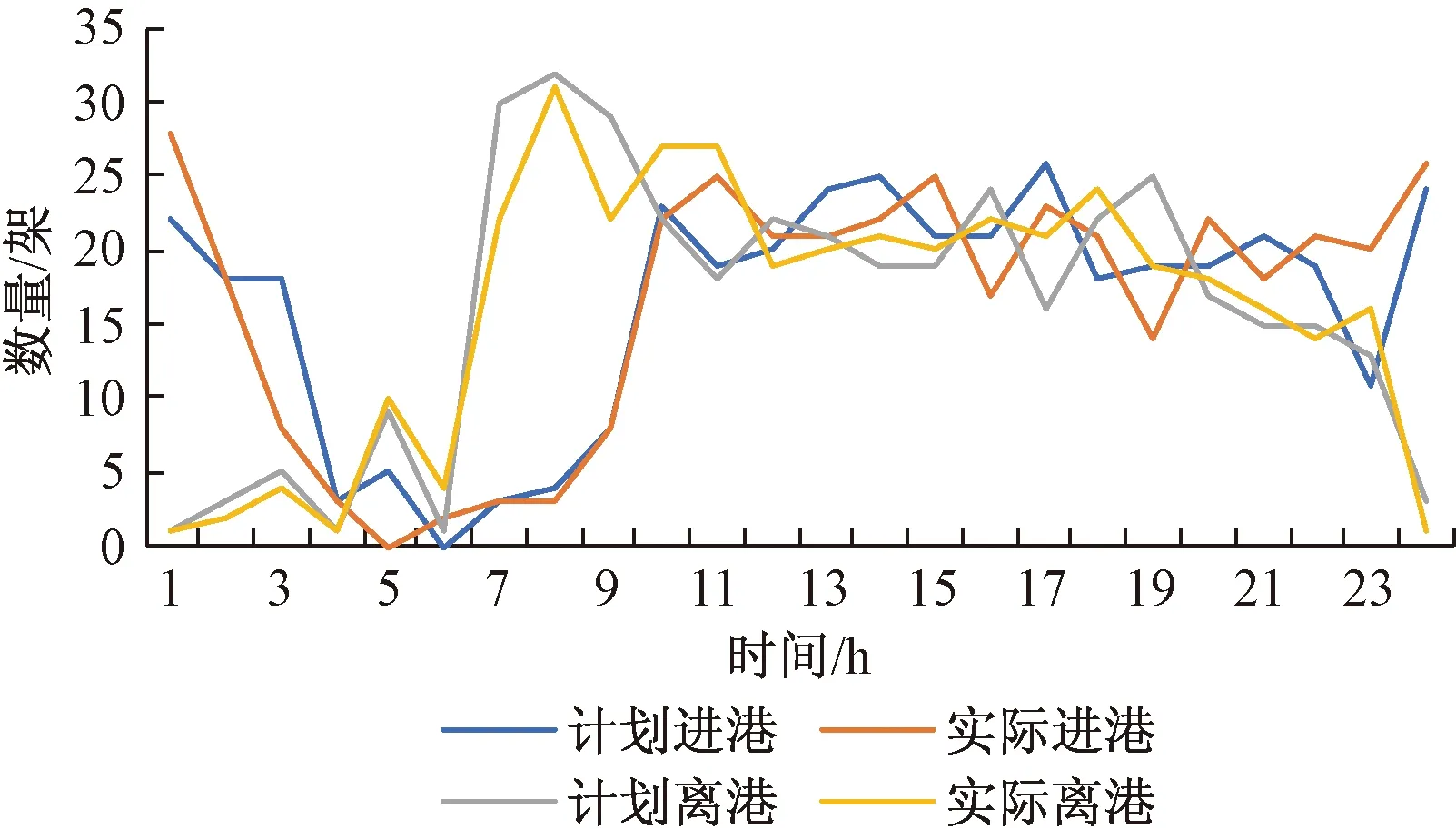
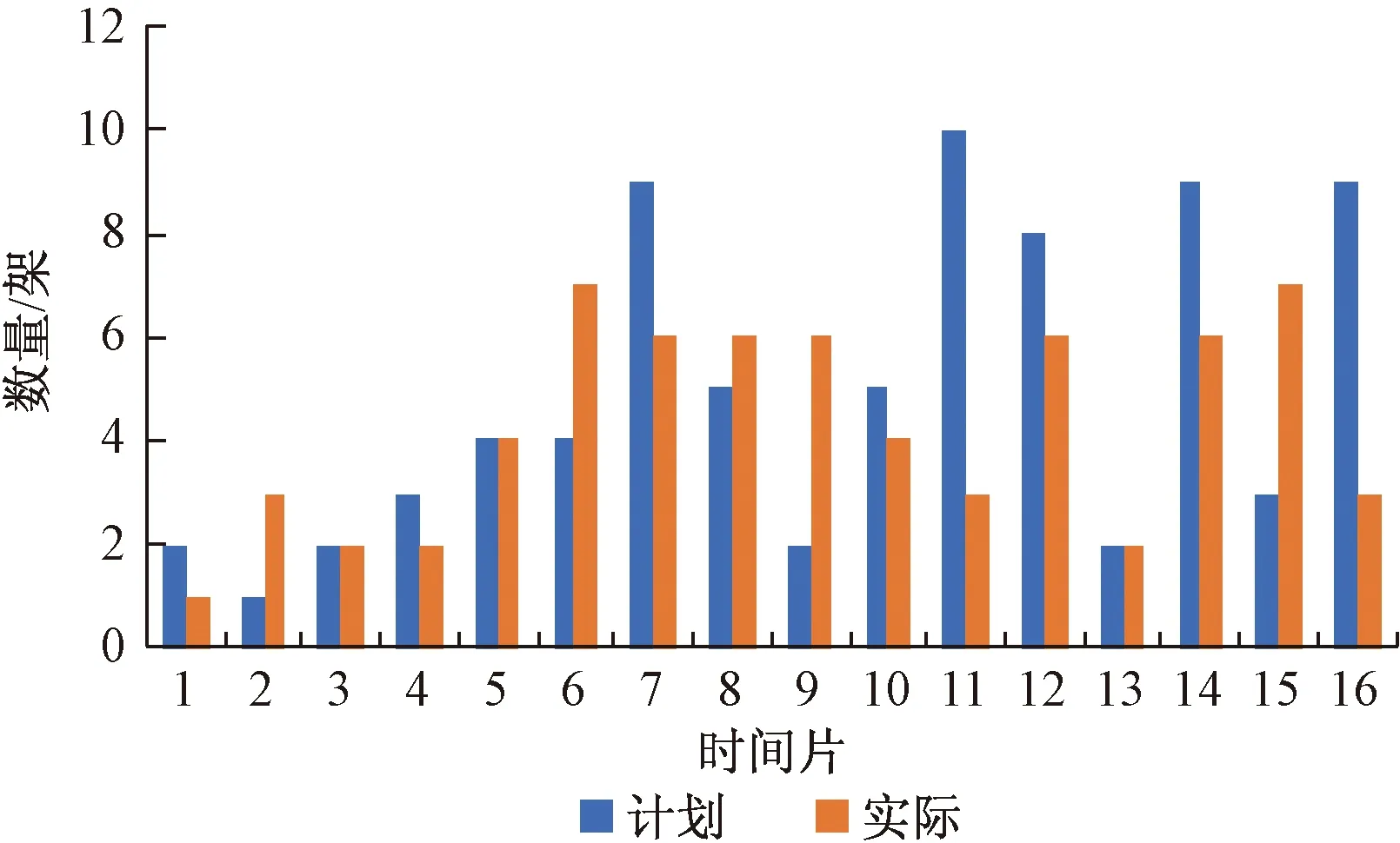
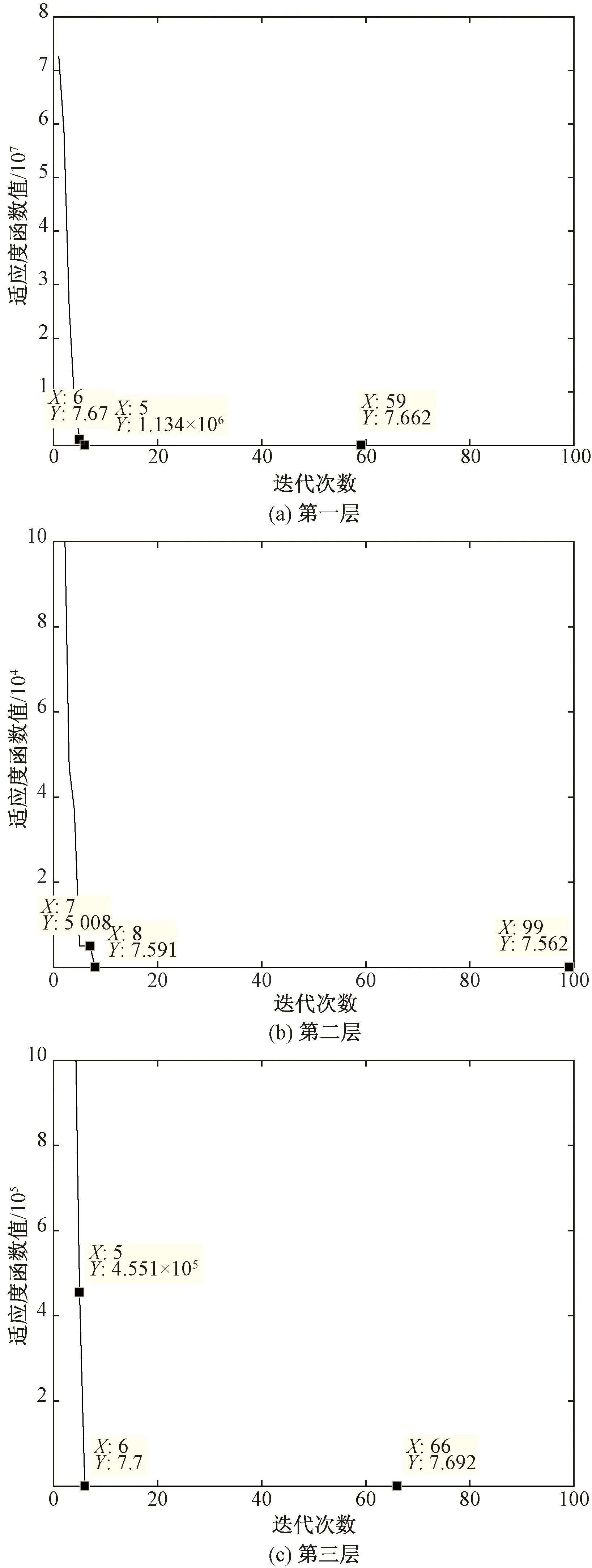
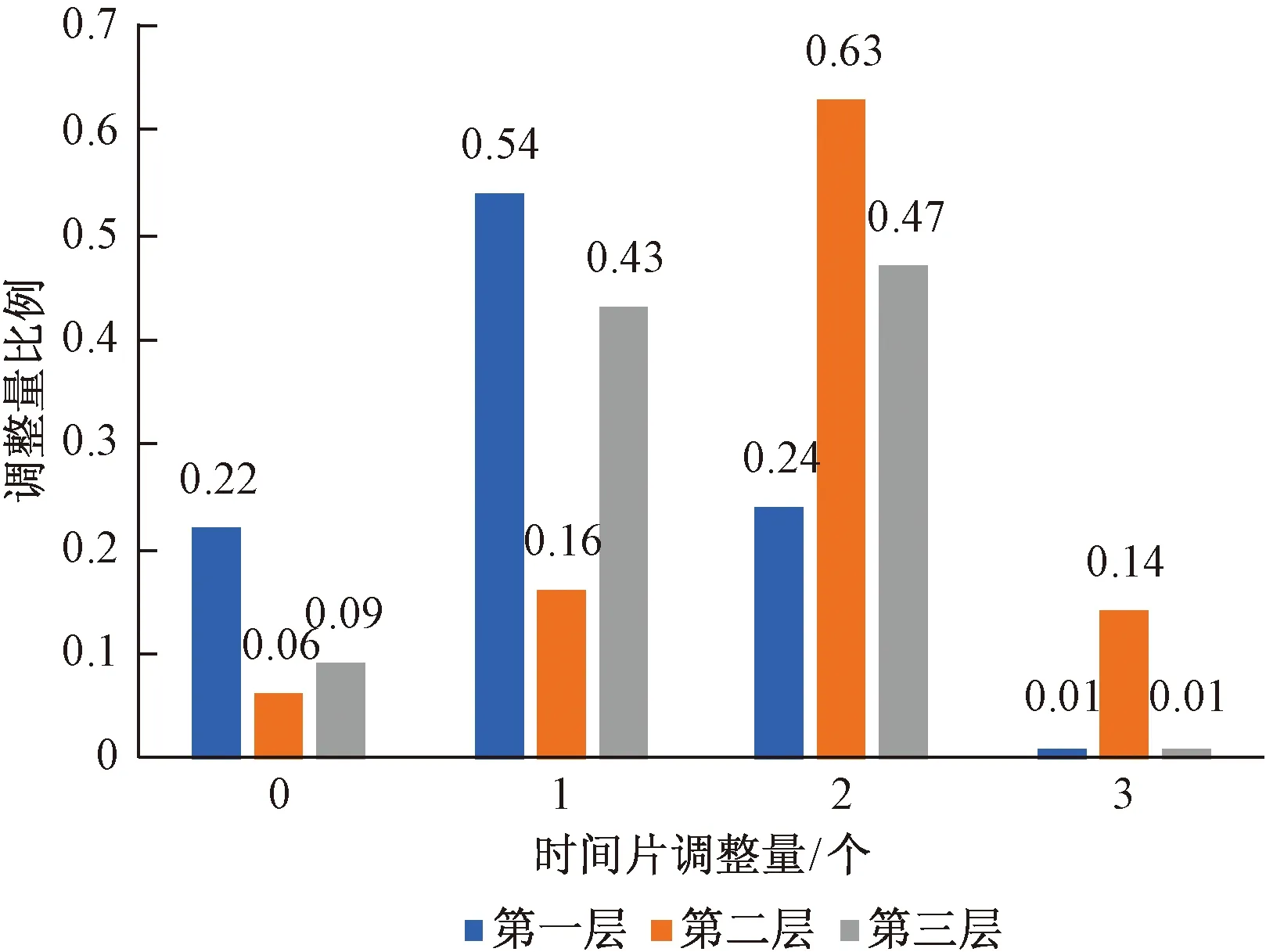
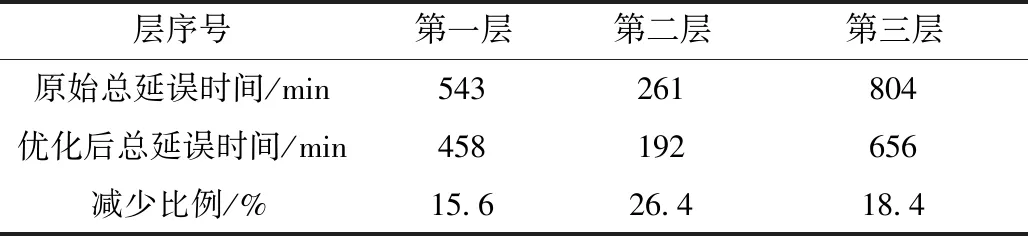
式(3)中:Ts={t∈T∣s 约束(2)保证每个航班只有一个时间片。 (3)轮挡相关时间随机性概率约束: ∀(i,j)∈D;∀acf∈ACF (4) Pr{ρi≤t′a,i-td,i+3}≥p2, ∀(i,j)∈D;∀acf∈ACF (5) 式中:Pr为概率;t′d,j为优化后后序航班撤轮挡时间;td,i为原始前序航班撤轮挡时间;t′a,i为优化后前序航班上轮挡时间;p1和p2分别为相应需要满足概率。 式(3)为机场在5、15、60 min内容量约束。式(4)为飞机在松弛时间内完成上轮挡的最低概率,也可理解为当有延误产生时利用松弛时间以p1的最低概率完全吸收或吸收部分延迟时间。式(5)为航班在计划到达时刻之后3个时间片(15 min)内上轮档的最低概率,此约束保证航班的准点率。 (4)原始航班时刻调整范围约束: |t′-t|≤θ, ∀t∈T (6) 式(6)中:t′为优化后上轮挡或撤轮挡时间;t为原始上轮挡或撤轮挡时间。 在众多寻优算法中,粒子群寻优算法应用广泛。经过几十年的发展,粒子群算法寻优理论不断改进完善。该算法通用性强不依赖于问题信息,可以协同搜索且收敛速度快,更容易飞跃局部最优解。但同时也存在一些问题,局部搜索能力差导致搜索精度不高且不能保证搜索到全局最优解,为此本文引进可以从多方面提高种群多样性的粒子群算法对模型进行求解。 传统粒子群算法的位置更新公式为 (7) (8) 改进后的位置更新方式可以提高种群多样性从而提高全局搜索能力,假如迭代运行后全局的极值保持不变,则选取m个粒子(m≤5%N,N为总粒子数量)的历史最优位置与当代产生的粒子进行重组,其位置更新公式为[18] hnew(xj)=(1-c)hold(xj)+c|hup(xj)- hold(xj)| (9) 式(9)中:hnew为新产生的粒子;hup为所选粒子的历史最优位置;hold为当代产生的粒子;c为(0,1)之间的随机数;xj为粒子第j维的位置。 异步学习因子使得在寻优初始阶段,粒子具有较大的自我学习能力和较小的社会学习能力,增强全局搜索能力;而在迭代后期,粒子具有较小的自我学习能力和较大的社会学习能力,增强局部搜索能力,其计算公式为 (10) (11) 式中:c1,ini、c1,fin为c1的初始值和最终值;c2,ini、c2,fin为c2的初始值和最终值,通常取c1,ini=c2,fin=2.5,c2,ini=c1,fin=0.5。 惯性因子主要影响了当前速度对上一代速度的继承,采用自适应惯性因子可以平衡算法的全局搜索能力和局部改良能力,其计算公式为[18] (12) 式(12)中:wmax、wmin分别为惯性因子的最大值和最小值;titer为当前迭代次数;Titer为最大迭代次数。改进的粒子群算法流程图如图4所示。 图4 改进粒子群算法流程图Fig.4 Flow chart of improved particle swarm algorithm 选取杭州萧山国际机场进行算例分析,该机场日均航班起降量800架左右。2021年4月3日该机场航班实际起落架次共计815架,当日每小时计划与实际的进离港航班量如图5所示。根据实际运行数据统计可知,当日上午8:00—12:00该机场计划进港航班为78架,而实际运行时出现延误现象,进港率出现较大波动。以15 min为时间片对8:00—12:00的计划进港与实际进港航班数量进行统计,从图6可以直观地看出,航班计划与实际进港量波动存在较大差异。 图5 进离港统计Fig.5 Statistics of arrivals and departures 图6 8:00—12:00计划与实际进离港图Fig.6 8:00 to 12:00 Plan and actual entry and departure map 故运用所提出的模型对该日8:00—12:00航班i的上轮挡时刻及其相应航班j的撤轮挡时刻进行优化,对原始航班时刻数据整理后部分数据如表3所示。经统计该时段内共有13趟航班进港时间达到晚点统计指标(超过计划时间15 min),占比该时段进港航班总量16.7%,共计延误543 min。其中有6趟航班离港时间因进港延误导致离港延误,共计延误261 min。 表3 原始航班时刻Table 3 Original flight schedule 根据1.2节所提出的轮挡相关时间理论依据进行合理假设,部分航班两阶段的分布信息如表4所示。 表4 两阶段时间量分布Table 4 Two-stage time distribution 由于机场容量相关数据的不可获取性,以5、15、60 min 3种时间间隔情景下每个情景中航班量上限占比最大的统计量作为各自情景的容量上限,具体信息如表5所示。 表5 机场容量信息Table 5 Airport capacity information 由1.5节建立的模型可知,需要对式(4)及式(5)分别赋予一个概率值p作为机场运行的最低要求。p1、p2的具体值可根据各机场实际情况要求进行设定,为方便计算且不失一般性在此设定p1、p2均为0.75作为计算示例。同理,设定目标函数权重系数ω1=ω2=0.5。 根据不同的要求,将所提出的模型划分为三层,三层模型无先后重要之分。第一层为模型中不含有式(5),即只要求航班在过站松弛时间内以p1的概率完成上轮挡。该层模型可减少离港延误时间,故对离港航班撤轮挡时刻进行优化调整。第二层为模型中不含有式(4),即只要求航班在规定时间延后15 min内以p2的概率完成上轮挡。该层模型可减少进港延误时间,故对进港航班上轮挡时刻进行优化调整。第三层为模型中同时含有式(4)和式(5),即同时达到第一层和第二层模型的要求。 在Win10环境下以MATLAB 2015b软件作为计算工具,对改进的粒子群算法设定粒子种群数量为20、所挑选的粒子数量m=5%N、迭代次数为100代,分别对三层模型迭代运算。第一层模型寻优结果如图7(a)所示,该层模型最优结果minz=7.662,效率目标值最大调整量为3个时间片即15 min,公平性目标值为0.324。第二层模型寻优结果如图7(b)所示,该层模型最优结果minz=7.562,效率目标值最大调整量为3个时间片,公平性目标值为0.124。第三层模型历代寻优结果如图7(c)所示,该层模型最优结果minz=7.692,效率目标值最大调整量为3个时间片,公平性目标值为0.384。 从结果可知,在三层模型中各模型的效率目标值均为3个时间片,也即由于实际情况在效率目标上均达到所限定的时间片最大调整量。其中第二层模型即只要求航班在规定时间延后15 min内以0.75的概率完成上轮挡的公平性目标值最小,其原因可能与所要求的最低概率或原始时刻安排有关。通过三层模型的迭代曲线可以明显看出,改进的算法在迭代时效果显著。以图7(a)为例,寻优迭代到第五代时迭代结果为数值较大,由算法流程判断条件当选取规定数量粒子的历史最优位置与当代产生的粒子进行重组后在第六代迅速脱离局部最优解。 图7 模型结果Fig.7 Model results 通过多次迭代统计所得,各层模型中0、1、2、3时间片(依次对应时间调整量为0、5、10、15 min)调整量所占比例各有不同,如图8所示。可以看出,第一层模型中,1个时间片的调整量比例值最大,最大为54%,同时也是三层模型中1个时间片调整量比例值中最大的。第二层模型中,2个时间片的调整量比例值最大,最大为63%,同时也是三层模型中2个时间片调整量比例值中最大的。在第三层模型中,2个时间片调整量占比最大,最大为47%。 图8 各层模型时间片调整量比例Fig.8 The proportion of time slice adjustments of each layer model 根据所建立的模型对该时段内航班时刻进行优化,优化后延误时间将得到有效削减,其各层模型延误时间优化结果如表6所示,结果显示利用第二层模型进行优化时优化延误削减可达到26.4%,其优化效果更为显著。 表6 三层模型优化结果Table 6 Three-tier model optimization results 从飞机轮挡事件的角度对航班时刻进行优化,模型中考虑撤轮挡时间和轮挡时间两个具有随机性的时间量。以航班时刻最大调整量最小作为效率目标函数,考虑到时刻调整的公平性问题使用泰尔指数作为公平性目标函数,利用改进粒子群进行迭代计算,得到以下结论。 (1)算例表明该模型可减少航班延误,对算例进行优化后,最高可减少26.4%的延误时间,最少可减少15.6%的延误时间。 (2)随机性约束条件可对航班时刻调整起到较好作用,根据不同要求可纳入不同约束。 在下一步研究中,可进一步对调整量和延误时间减少量之间权衡以及减少航班提前到达的时间等问题进行深入考虑,增强其应用价值。2 模型求解算法
2.1 位置更新改进

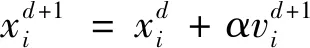

2.2 异步学习因子


2.3 自适应惯性因子


3 算例分析
3.1 数据处理


3.2 运算结果分析
4 结论

