基于四阶段模型的深埋硐室围岩分区受力分析

孙卫星，赵永宾，周 建，杨新安

(1.中交第三航务工程局有限公司交建分公司，上海 201900；2.同济大学道路与交通工程教育部重点实验室，上海 201804)

长期以来,硐室围岩的支护问题一直是学术界研究的重点[1-4]，随着硐室埋深与地应力的不断增大，硐室开挖过程中选择何时支护存在诸多疑惑[5-8]。目前，硐室围岩开挖后的支护理论已趋于成熟，众多学者进行了大量该方面研究。任青文等[9]选择第一主应力的屈服范围，在衬砌作用下得出围岩应力计算公式和适用条件；余伟健等[10]将锚杆与锚索联合支护组成叠加拱，得到了叠加拱强度的解析解；吴顺川等[11]基于Mohr-Coulomb 屈服准则，提出在广义荷载作用下巷道围岩与衬砌结构相互作用的弹塑性解析表达式；李鹏飞等[12]、王明斌等[13]考虑地应力释放，得到含衬砌的圆形隧道应力、变形解；上述文献虽然得出了支护条件下围岩的弹塑性解，但均考虑的是硐室的二维问题，没有结合硐室的施工过程，有关硐室开挖过程中施工理论研究亟待发展。

由于传统的硐室弹塑性分析是以二维平面应变为基础，为体现硐室开挖与支护的全过程，则有必要考虑空间效应。空间效应的定义为：由于开挖面的支撑作用，使得已开挖部分硐壁位移得不到充分释放，某一断面的弹塑性变形随着与工作面距离的远去而逐步地释放直至完成的现象[14]。近年来，关于此方面的硐室开挖围岩理论取得一定进展。王华宁等[15]考虑隧洞断面与纵向开挖及双层衬砌的施工过程，给出不同支护时机围岩软化区与破裂区范围及支护力、围岩应力与位移的理论解答；赵光明等[16]基于统一强度屈服准则，考虑空间效应，分析了围岩在锚网喷作用下的力学机制。然而，对于软岩而言，从软岩硐室岩石的全应力-应变曲线中不难发现，软岩具有明显的塑性硬化和塑性软化阶段。研究表明，塑性硬化区和塑性软化区对围岩自承能力起主要作用，所以塑性硬化区在软岩硐室弹塑性分析中不容忽视[17]。张俊文[18]获得了泥岩和砂质泥岩应力-应变曲线，发现大规模软岩在峰前具有明显的非弹性变形阶段，软岩峰前硬化对围岩塑性区应力、位移解有重要的影响。不难看出，传统的理想弹塑性模型(二阶段模型)与应变软化模型(三阶段模型)不足以反映围岩的破坏过程，应考虑硬化特性。孙振宇等[19]认为初衬需考虑混凝土硬化时效性，混凝土喷射后硬化过程需要一定时间，因此，考虑混凝土硬化的时效特性更符合现场实际应用。

在前人研究的基础上，根据Mohr-Coulomb准则，将硐室围岩分为弹性区、塑性硬化区、软化区和残余区，考虑扩容、剪胀等岩石特性、空间效应、锚杆与围岩的耦合作用以及初衬混凝土的时效特性，给出了软岩硐室在开挖-支护过程中围岩应力、位移的理论解答，并对塑性区的影响因素进行分析，为硐室支护前后应力、位移提供了较为准确的理论方法。

1 理论模型与假定

根据硐室围岩破坏特征，圆形硐室围岩分区如图1所示，并做出以下假定：①近似地认为硐室无限长，岩体为各向同性、均质的连续介质；②取硐室断面为圆形，半径为r0，残余区半径为Rb，软化区半径为Rp，硬化区半径为Rh，残余区半径为Rb；③静水压力为p0，衬砌提供支护阻力为pi。

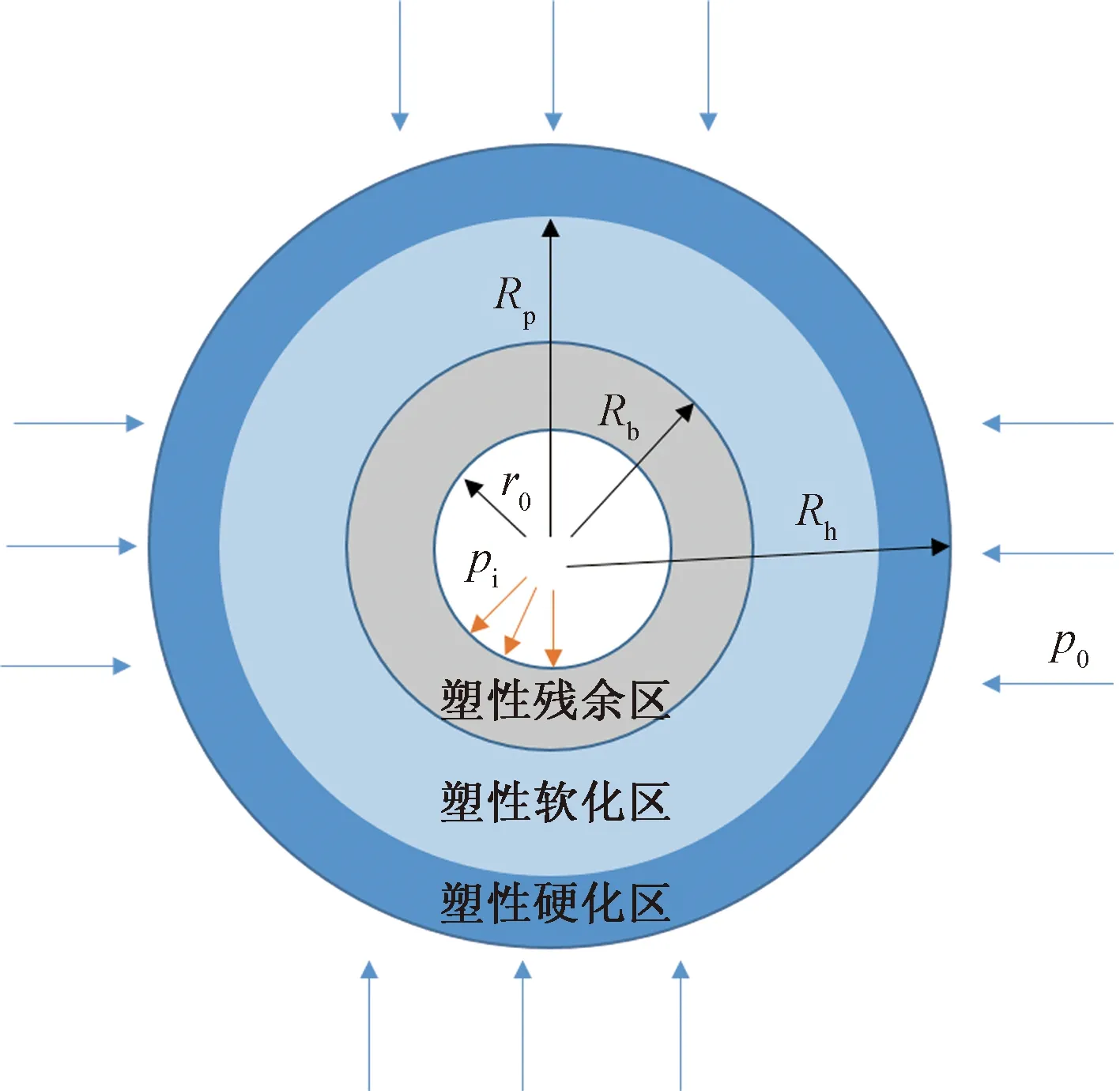
图1 硐室围岩弹塑性区域图Fig.1 Elastic-plastic deformation zones of surrounding rock

σθ、σr分别为圆形硐室围岩的切向、径向应力，满足σθ>σr；εθ、εr分别为围岩的切向、径向应变；上角标e、h、p、b分别为弹性区、硬化区、软化区及残余区。

1.1 初始支护承载力

硐室掘进过程中，“空间效应”引起的虚拟支护阻力表达式为[20]

(1)

式(1)中:p1为虚拟支护阻力；V为巷道平均掘进速度；t为巷道断面开挖瞬间的起始时间。

初始支护承载力pc可表示为

(2)

式(2)中:t0为开始支护时的时间。

1.2 围岩硬化和软化模型

将围岩硬化、软化模型简化成四段线，如图2所示。

分别为弹性区和硬化区交界处、硬化区和软化区交界处、软化区和残余区交界处的切向应变；cm、c0、cb分别为岩石峰值强度、单轴抗压强度和残余内聚力图2 内聚力硬化、软化模型Fig.2 hardening and softening model of cohesion

岩体达到屈服强度后，进入硬化阶段，达到峰值强度时，开始软化直至降为残余强度，在硬化阶段和软化阶段，假定岩体强度与应变呈线性变化。

围岩各区服从Mohr-Coulomb准则，有

(3)

(4)

(5)

软化区有

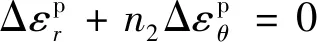
(6)

残余区有

(7)

2 支护前硐室围岩弹塑性分析

2.1 基本方程

根据弹塑性理论，围岩满足平衡方程:

dσr/dr+(σr-σθ)/r=0

(8)

式(8)中:r为围岩某点至隧道中心的距离。

几何方程为

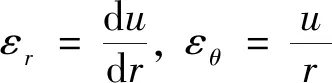
(9)

式(9)中:εr、εθ分别为围岩的径向、切向应变；u为围岩径向位移。

2.2 弹性区应力、位移

考虑空间效应时弹性区应力为

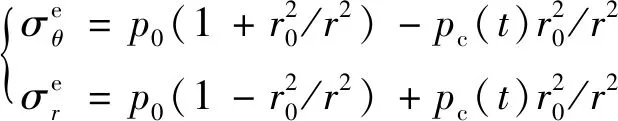
(10)

径向位移为

(11)

2.3 硬化区应力、位移

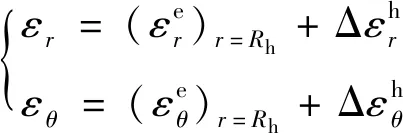
(12)

由式(12)、式(9)和式(5)可得该区位移协调方程，并由边界条件r=Rh处的位移连续可得

(13)

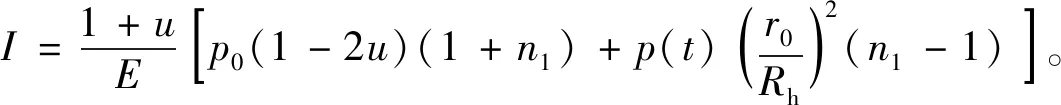
将式(8)和式(3)中第2个公式联立，且由边界条件r=Rh处径向应力相等得

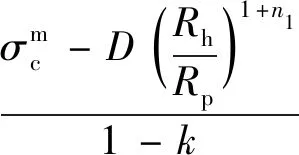
(14)

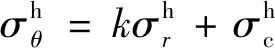
(15)

2.4 软化区应力、位移

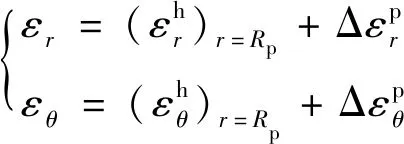
(16)

由式(16)、式(9)和式(6)可得该区位移协调方程，并由边界条件r=Rp处的位移连续可得

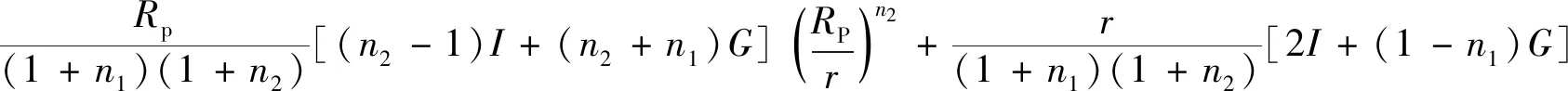
(17)

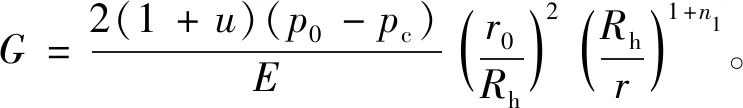
将式(8)和式(3)中第3个公式联立，且由边界条件r=Rp处径向应力相等得

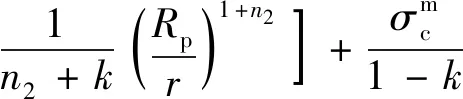
(18)

(19)

2.5 残余区应力、位移

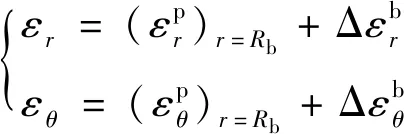
(21)

由式(20)、式(9)和式(7)可得该区位移协调方程，并由边界条件r=Rp处的位移连续可得

(22)

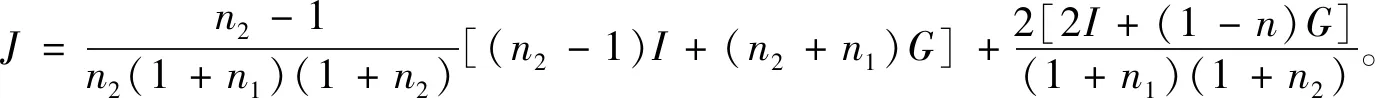
将式(8)和式(4)中第4个公式联立，且由边界条件r=Rb处径向应力相等得

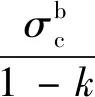
(23)

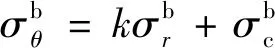
(24)

2.6 硬化区、软化区和残余区范围

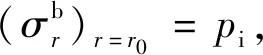
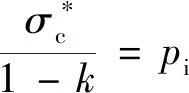
(25)

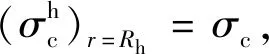
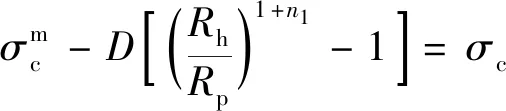
(26)

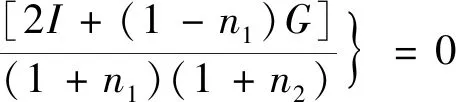
(27)

将式(25)～式(27)联立方程组，可解出Rh、Rp和Rb。

3 支护结构与围岩的耦合作用

假设支护结构锚杆和衬砌与围岩紧密接触，锚杆与围岩耦合看成复合承载体，锚杆与衬砌施加的时间差近似为0。另外，考虑混凝土强度硬化的时效性，锚杆与衬砌共同承担围岩荷载。

3.1 围岩与锚杆耦合作用下的等效材料参数

由于锚杆与围岩的支护作用力以等效体积力的形式作用于围岩[21-22]，塑性硬化和塑性软化区应力、位移与半径呈非线性变化，当锚杆锚固端作用于这两段时，求解围岩应力、位移较为复杂，假设锚杆覆盖塑性区简化计算。根据文献[23],采用均匀化法将锚杆均匀布置，锚杆与围岩视为等效材料，等效材料弹性模量表达式为

(28)

式(28)中：Eb为锚杆弹性模量；rb为锚杆直径；E为围岩弹性模量；f1为锚杆排距，f2为锚杆环向间距。

然而，文献[23]中的等效内聚力和等效内摩擦角确不能采用，主要存在两个问题:①量纲量与无量纲量不能相加减；②均匀化法并没有考虑锚杆预紧力(预紧力主要对围岩内聚力有影响)，等效材料的参数计算会有偏差。当硐室围岩开挖后产生塑性区时，其内摩擦角较弹性区小，在塑性区施加锚杆时，其内摩擦角会接近于弹性区，故认为等效材料的内摩擦角与弹性区近似相等。对于等效材料的内聚力，根据文献[24],考虑锚杆预紧力的等效材料内聚力c*为

c*=ci+cd+ct

(29)

将等效材料参数E*，c*(φ不变)代入上述公式，可得到锚杆支护后的围岩应力、位移以及各分区范围。

3.2 混凝土喷层支护时的位移解析

混凝土喷层施作后便被动受压而提供支护阻力，但喷层具有一定承载能力则需一个时间过程，其强度主要与弹性模量相关，文献[25]通过声波法获得混凝土弹性模量与龄期的关系式，可表示为

(30)

式(30)中:E0为混凝土喷层最终弹性模量；α、β为经验值，取值可参考文献[26];t1为混凝土喷层达到设计强度的时间。

当锚杆和围岩看作复合承载体后，复合承载体的荷载由衬砌支护阻力和虚拟支护力承担。硐壁的径向位移可表示为

ub|r=r0=r0n3[pi(t)+p1(t)]

(31)

对于给定的时间增量Δt，硐壁径向位移增量为

(32)

将混凝土喷层等效为刚度为Kc的曲梁，支护引起的硐壁位移增量型本构方程为

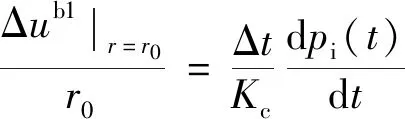
(33)

虚拟支护力引起的硐壁位移增量型本构方程为

(34)

式(34)中:s为积分参数。

4 算例分析

设计圆形硐室基本参数如下：硐室半径r0=3 m,岩体力学特征参考文献[18]：E=2 000 MPa,泊松比μ=0.32,p0=20 MPa,c0=0.8 MPa,cm=1.6 MPa,cb=0.4 MPa,φ=30°；pi=0 MPa,计算得到n1=3，ψ=10°，n2=1.42，n3=1.4。锚杆覆盖非弹性区，具体参数如下:弹性模量Eb=210 GPa，屈服强度σb=345 MPa,预紧力F=60 kN,半径rb=20 mm,间排距f1=f2=600 mm。衬砌参数如下：E0=2.8×104MPa,厚度为r0-a=0.25 m。考虑到支护时机，若开挖进度V=3 m/d，秉承开挖一段支护一段的原则，选择开挖1 d(t0=1 d)后支护前一天开挖段。支护前后，硐室分区范围如表1所示。

从表1可以看出，无支护时，硐室在高地应力下残余区厚度达1.87 m,有支护时支护残余区厚度只有0.96 m，支护可以有效减小塑性区范围。考虑空间效应时，塑性各区范围进一步减小，另外，开挖面距支护面的距离越短，则“空间效应”越明显。

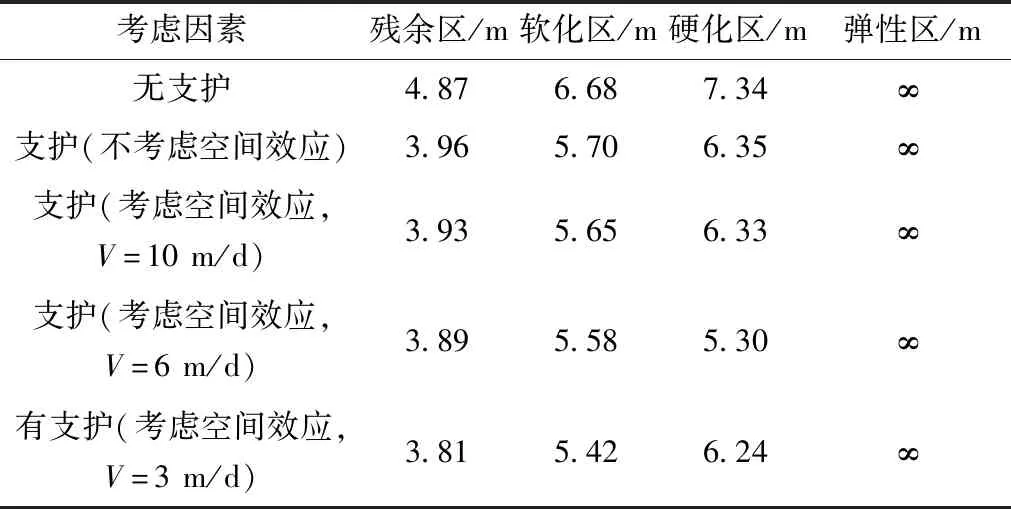
表1 硐室围岩各分区范围Table 1 The surrounding rock failure zones of chamber

3.1 锚杆间排距对硐室应力、位移的影响

由图3可知，围岩切向应力在硬化区和软化区交界处达到最大值。间排距越大，切向应力和径向应力越小，切向应力峰值向远离硐室中心的方向移动，不利于硐室安全。径向应力在软化区半径处有个拐点，在软化区内发展较快，而在硬化区内径向应力发展平缓。在软化区切向应力急剧上升，而硬化区急剧下降，弹性区趋于平稳。虽然锚杆间排距缩小能增大围岩应力，加强塑性区承载力，但增大幅度不大。图4显示，当间排距越大，围岩位移越大，间排距主要影响塑性区位移，而对弹性区位移的影响几乎很小，当r=3 m时，将间排距1.2 m锚杆支护下围岩位移与间排距0.4 m进行对比，后者比前者位移减小35.6%，所以，锚杆间排距对硐室的影响主要体现在围岩位移上。

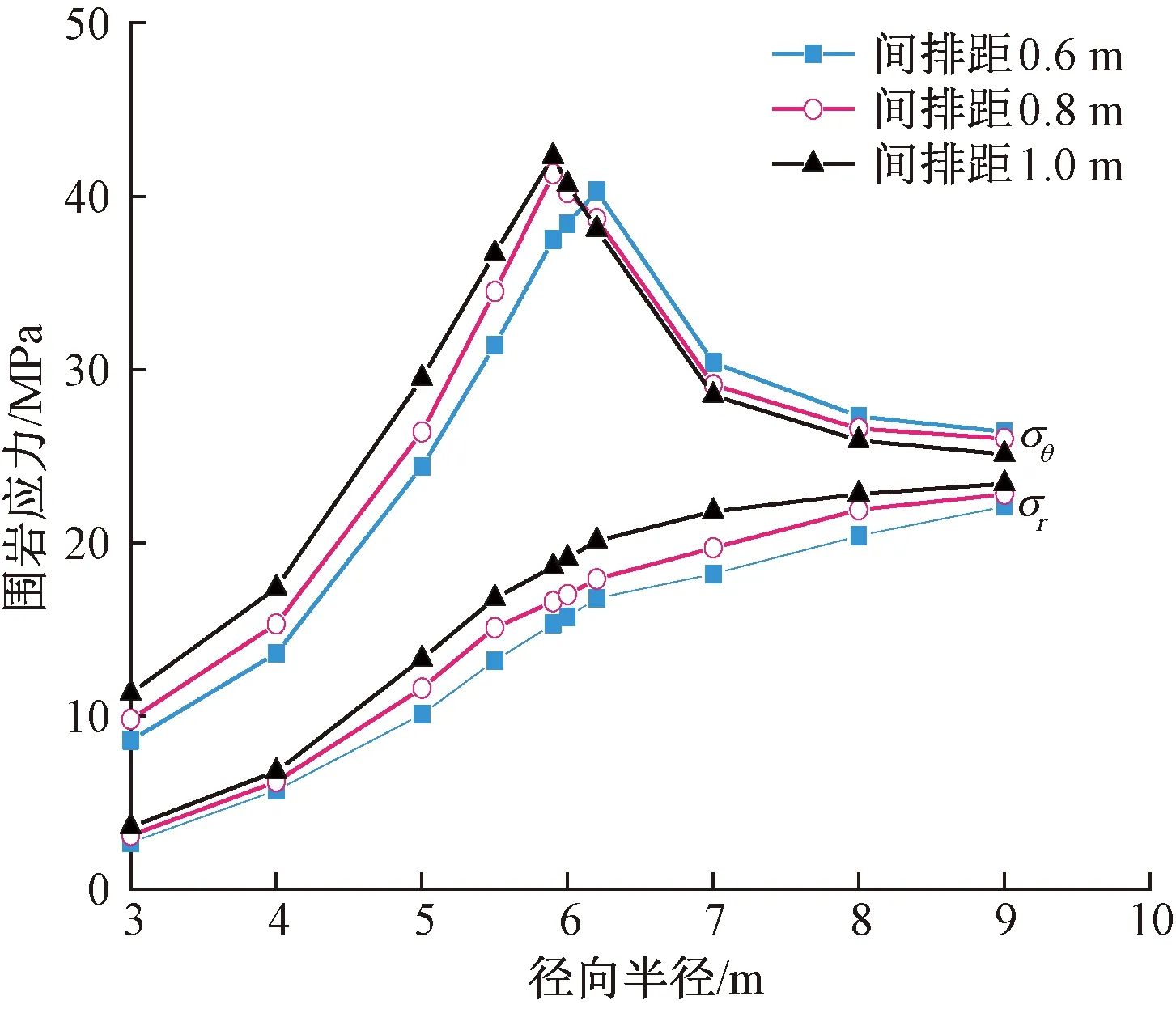
图3 锚杆间排距对围岩应力的影响Fig.3 Influence of Inter-row spacing of bolts to stress of surrounding rock

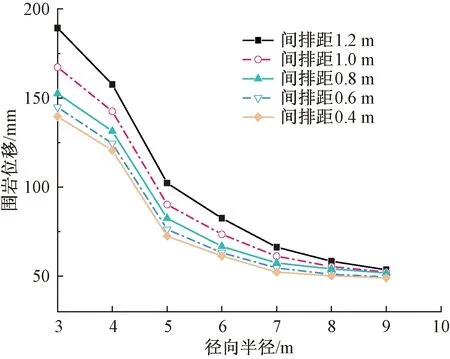
图4 锚杆间排距对围岩位移的影响Fig.4 Influence of inter-row spacing of bolts to displacement of surrounding rock

3.2 硬化区扩容系数对硐室周边位移的影响

由图5可以看出，围岩位移随着剪胀角的增大而增大，当ψ≥15°时，u受剪胀角的影响较大。将n1=3.5与不考虑扩容时的围岩位移进行对比前者比后者增大41.5%～52.5%,则 硬化区扩容系数对硐室周边位移的影响较大，说明当岩石有明显的硬化区时，若不考虑围岩硬化扩容将错估围岩位移发展，则威胁支护结构的安全。

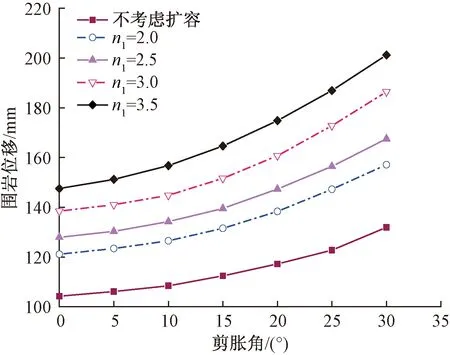
图5 硬化区扩容系数和剪胀角对硐室周边位移的影响Fig.5 Influence of dilatancy of plastic hardening zone and dilatancy angle to surrounding displacement of chamber

3.3 空间效应和支护时机对硐室围岩位移的影响

令开挖面与支护面的距离为x，且x=Vt0，则x与空间效应有关。空间效应对硐室围岩位移的影响如图6所示，x值越小，虚拟支护阻力越大，支护面与开挖面的距离越短，则硐壁径向位移越小，越有利于硐室稳定。将x=15 m时的围岩位移与不考虑空间效应和支护时机进行比较,前者在r=3 m处的位移相当于后者的95.9%，当x≥15 m，可以忽略空间效应对围岩位移的影响。

|V|为支护时距开挖面的距离图6 空间效应对硐壁径向位移的影响Fig.6 Influence of space effect and to surrounding rock displacement of chamber

软岩硐室开挖过程中，一般对已开挖部分先喷一层混凝土抑制围岩变形，而后施加锚杆。关于支护时机对围岩位移的影响如图7所示，在支护施加之前，硐壁已经产生一段位移，可记为u0，支护施加后硐壁产生的位移记为u1。当掘进速度一定的条件下，x与t0呈正相关，t0越大，u0越大，u1越小，但u0增大速率远大于u1，硐壁的总体变形在增大，这是由于t0较大时，支护之前硐壁已经产生较大位移，支护抑制围岩位移有限，如t0=6 d时，u1仅为u0的3.4%，相反，t0较小时，如t0=1 d时，u1占u0比值为28.8%，总位移仅相当于t0=6 d时的60.7%，支护效果明显。

图7 支护时机硐壁围岩位移的影响Fig.7 Influence of supporting opportunity to surrounding rock displacement of chamber

4 结论

研究了深埋圆形硐室开挖过程中围岩破裂分区以及考虑支护时机的围岩弹塑性理论，得出以下结论。

(1)基于Mohr-Coulomb 屈服准则，考虑围岩软化、剪胀等特性将硐室围岩四分区，并引入空间效应，得到了无锚杆、衬砌支护下围岩的应力、位移及各分区范围解析式。支护过程中将锚杆在硐室中均匀布置，与围岩组成复合承载体，合理计算等效材料参数，且考虑混凝土喷层的硬化时效特性，得到了支护条件下围岩的弹塑性解，理论计算以往文献更接近现场工程实践。

(2)结合算例分析，得到了硐室支护前后各分区范围变化情况，支护条件下能够有效地缩小塑性区范围且主要缩小残余区范围，考虑空间效应和支护时机更能准确地计算各分区范围；对硐室围岩应力、位移的影响因素进行分析，得到了锚杆间排距对围岩应力影响不大，而对围岩位移的影响主要体现在残余区；分析了硬化区扩容系数对围岩位移的影响，认为软岩硐室分区计算不能忽视硬化区。

(3)着重分析了空间效应和支护时机对硐室围岩位移的影响，认为当x较小时，空间效应不容忽视，当x≥15 m，可以忽略空间效应；对于支护时机，当t0≥6 d时，支护对围岩位移的限制有限，t0较小时，支护效果明显。理论研究为软岩硐室设计、施工提供一定的理论依据。