小半径曲线连续箱梁桥恒载应力的空间分布特性分析

冯升阳，郭增伟*，赵付强

(1.重庆交通大学土木工程学院,重庆 400074;2.中交路桥建设有限公司,北京 100027)

随着时间的推移和技术的进步，中国桥梁工程正迅速发展[1]。在各类桥梁建设中，小半径大纵坡弯曲混凝土桥因具有布置灵活、不受施工场地限制等优点成为市政桥梁及高架桥的重要组成部分[2]。自20世纪80年代始，中国越来越多的城市立交桥及匝道桥工程偏向于选择曲线桥，如南京的中央门立交桥，天津的中山门立交桥等[3]，用以解决许多复杂的交通问题。虽曲线箱梁桥相较于曲线“T”梁桥等其他桥型而言整体性较好[4]，但曲线桥因曲率的影响不仅会产生弯矩，还会产生极大的扭矩，所以受力更为复杂[5]；当曲线桥受到扭转和竖向弯曲时，其箱梁截面会发生约束扭转和截面畸变，使得腹板及截面应力分布极不均匀，其截面的空间受力效应也更加显著[6]。

在曲线箱梁桥设计中常用的分析计算方法大致有：理论分析计算：荷载横向分布计算、梁格系分析等的近似方法；有限元数值分析计算：基于梁系、杆系理论的有限元法和基于实体单元、板壳单元的有限元法等[7]，在计算曲线桥梁时通常是用基于梁格系理论的有限元方法计算荷载效应的横向分配及空间分布，其计算结果不能真实的反应箱梁在空间上各处的受力分布情况[8]，导致在建和已建桥梁产生各类桥梁病害，如曲线箱梁的空间扭转导致腹板开裂、内侧支座脱空、梁端侧向爬行等[9-10]。

目前，中外学者对曲线桥的空间受力特点开展了大量研究。Agarwal等[11]采用有限元方法对一座单室钢筋混凝土斜弯箱梁桥进行了恒载和印度道路协会规范(Indian Roads Congress，IRC)活载作用下的研究，并将计算结果与同跨径直桥相比，研究表明外腹板受偏度和曲率的影响大。Gupta等[12]利用CSiBridge有限元计算软件以某单跨斜弯桥为工程背景，对不同偏斜角和不同中心曲率角下的模型进行了分析，指出曲率和偏斜度都是影响斜弯桥受力响应的关键参数。刘小燕等[13]以某曲线T梁桥为工程背景，利用实体单元有限元法，对其进行应力分析，对比同跨径的直线梁桥，指出曲线T梁桥因曲率因素对外边梁受力不利，但对内边梁受力有利，同时对中梁受力的影响有限。何庆华等[14]以某曲线桥梁为工程背景建立有限元模型，分析一期恒载作用下，主梁截面在不同曲线半径时的正应力及剪应力分布，指出箱梁截面正应力分布受剪力滞影响外，内外侧弧长不等也会影响其空间分布。Wang等[15]通过曲线宽箱梁的有机玻璃模型试验，以及有限单元法(finite element method，FEM)分析三跨曲线连续宽箱梁桥(半径110 m，跨径16 m，圆心角为8.33°)的空间受力、内力横向传递机理和扭转耦合效应，提出了均匀系数来表示曲线桥受力的不均匀性，指出在腹板和顶板的交界处应力出现极大值，曲线宽箱梁空间受力极不均匀，外侧挠度大于内侧，且箱梁应力不均匀性小于挠度不均匀性。

若不充分考虑曲线箱梁桥复杂的空间受力特性，可能会导致这类桥梁在建设及使用过程中出现严重的桥梁病害。因此，为了给曲线箱梁桥的合理设计提供理论依据，现以某混凝土曲线箱梁桥为工程背景，建立实体单元有限元模型，计算不同标准跨径，分析曲线箱梁桥的恒载效应，对比同跨径直线桥梁在内力和应力上的差异，为曲线箱梁桥的设计提供参考。

1 工程背景及有限元模型

1.1 工程背景

某城市立交匝道部分曲线箱梁桥，跨径布置为5×18.76 m，桥梁位于圆曲线半径R=105 m的平面上，桥梁设置单向2%的横坡，桥梁纵坡为3.35%，桥梁全长93.8 m。主梁为单箱双室截面，箱梁顶部全宽9.75 m，顶板厚25 cm；底板宽5.13 m，底板厚42 cm；梁高2 m，中腹板厚55 cm，两边腹板厚55 cm，倾角60°；主梁采用C50混凝土，结构体系为五跨一联连续箱梁，主梁标准断面如图1所示。

1.2 有限元模型

为准确的分析混凝土曲线梁桥的空间受力分布规律，使用柱坐标并以曲线箱梁桥平曲线圆心为坐标原点，顺桥向方向为Y轴，横桥向方向为X轴，箱梁竖向为Z轴建立ANSYS实体有限元模型。主梁材料为钢筋混凝土，在有限元软件中采用SOLID65单元模拟，为保证计算精度，使用六面体映射网格，网格尺寸为0.12 m(圆曲线半径105 m，跨径16 m的有限元模型共956 394个节点，822 400个单元)。模型涉及滑动支座和固定支座，其中关于滑动支座则约束支座中心线位置的箱梁底板底缘、节点的竖向和径向自由度，固定支座则采用约束支座中心线位置的箱梁底板底缘的节点3个方向自由度的形式模拟；同时根据文献[16]，桥梁中墩全部采用抗扭支座。

为验证ANSYS实体单元有限元模型的正确性，在Midas/Civil中建立同跨径、相同约束的有限元模型。在Midas/Civil有限元软件中，通过控制单个梁单元长度，“以直代曲”模拟曲线箱梁桥；滑动支座和固定支座用一般支承分别约束相应的Dx、Dy、Dz来模拟不同的支座约束。由于ANSYS实体模型与Midas/Civil杆系结构模型的计算结果表示方式不同，拟就截面内力对两种有限元软件计算结果进行对比。图2给出了跨径16 m(圆心角为8.73°)的曲线箱梁桥的两种有限元软件内力计算结果相对误差情况；ANSYS有限元模型采用对截面应力积分的方式获取截面竖向弯矩和剪力，支反力是对每个约束位置的节点反力求和所得；控制截面为每跨跨中截面及支点截面。

由图2可知，在恒载作用下，ANSYS实体模型各约束位置处支反力与Midas/Civil杆系结构模型计算所得支反力基本一致，误差在±5%以内。Midas/Civil计算结果与ANSYS各控制截面应力积分计算所得竖向弯矩和剪力的相对误差约在10%左右，竖向弯矩最大相差13%，竖向剪力最大相差21%，这是由于曲线箱梁桥的“弯扭耦合”以及“剪力滞”作用，导致基于梁系结构的Midas/Civil在计算曲线箱梁时计算结果精度不足，不能真实的反应箱梁截面的受力分布特性。为解决基于平截面假定的初等梁单元理论计算不准确的问题，拟用 ANSYS 实体有限元法模型计算结果对箱梁的空间受力进行分析。

2 曲线箱梁恒载应力的空间分布

在一期恒载作用下，曲线箱梁桥主要存在弯曲、扭转、截面畸变等变形，其截面正应力则主要由弯曲应力、扭转应力组成，而剪应力主要为竖向弯曲剪应力[6]。曲线箱梁桥相对于直线箱梁桥，箱梁截面的空间应力更为复杂。图3、图4分别给出了跨径45 m，圆心角为24.56°的曲线箱梁桥在恒载作用下边跨跨中箱梁截面纵向正应力、竖向剪应力分布云图。

从图3可知，曲线箱梁桥第一跨跨中截面法向正应力在同一高度上沿横向分布不均匀；从图4可知在跨中截面处，箱梁竖向剪应力呈现外侧腹板远大于内侧腹板的现象，初步验证曲线箱梁桥因“弯扭耦合”作用导致的“外侧加载，内侧卸载”的规律。针对两种不同的现象，主要分析曲线箱梁桥和直线桥的腹板剪力差异和截面法向正应力差异。

为了更好地评价箱梁截面各区域对截面内力的贡献，可将截面分成7个不同的区域，将ANSYS计算所得截面各个区域内的法向正应力对截面形心积分计算，得到各个区域承担的弯矩值；对各个区域内的竖向剪应力应力积分得到各个区域承担的竖向剪力值；以积分所得截面总内力(弯矩、剪力等)为基准，计算截面各个分区内力承担比例，可得弯矩承担比例为PMi和剪力承担比例PQi的计算公式为

(1)

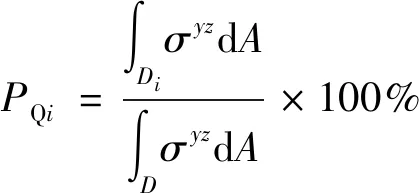
(2)

式中：σy和σyz分别为在ANSYS实体模型计算结果中的法向正应力和竖向剪应力；dA为实体单元在积分投影截面的投影面积；y为实体单元形心距离积分投影截面形心的距离；Di为各分区积分投影面积；D为整个积分投影面积。

1～7为箱梁分区图3 边跨跨中截面正应力分布云图Fig.3 Normal stress distribution of the middle section of side span

1～7为箱梁分区图4 边跨跨中截面剪应力分布云图Fig.4 Shear Stress distribution of the middle section of side span

对比分析曲线箱梁桥与直线箱梁桥，将内力比例系数PMi、PQi进行无量纲处理得内力比值系数ξ，从而得到各分区的内力比值系数定义为

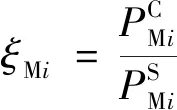
(3)

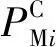
(4)

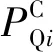
经计算，表1给出跨径45 m时曲线箱梁桥边跨控制截面各分区内力分担比例。

表1 截面各分区内力占比Table 1 Internal force proportion of each section

3 曲线、直线箱梁桥受力分布对比

曲线箱梁截面应力的不均匀分布主要是箱梁的薄壁效应和曲梁的弯扭耦合效应所导致的，为分析曲梁的弯扭耦合效应对恒载内力分布的影响，拟采用图1所示箱梁横断面，从16、25、35、45 m常用标准跨径计算分析曲线梁桥的空间受力分布规律，对应圆心角分别为8.73°、13.64°、19.10°和24.56°。

3.1 剪力分布差异分析

经计算，曲线梁桥在一期恒载作用下，对比同跨径的直线梁桥，二者在各控制截面的总剪力值和总弯矩值差异不明显，这与文献[14]的结论一致，但各腹板区域承担剪力占比相较于直线桥梁差异极大，尤以边跨最为显著。

表2给出了不同跨径下边跨跨中、支点截面各腹板剪力承担比例。通过无量纲化处理，内侧腹板的剪力比值系数由图3、图4所示的2号分区计算所得，中腹板由4号分区计算所得，同理，外侧腹板由6号分区计算所得。

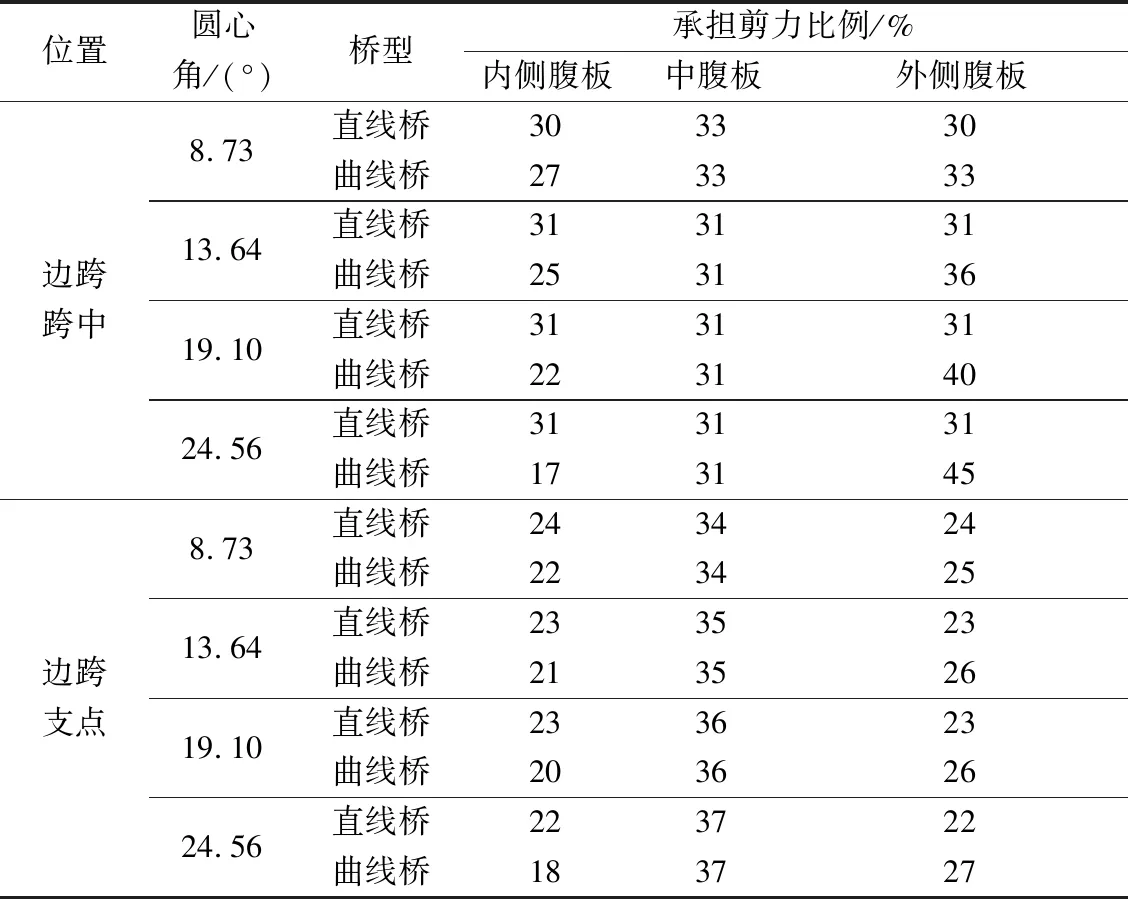
表2 不同跨径下腹板承担剪力比例Table 2 Shear ratio coefficient of webs under different span

从表2可知，直线箱梁桥的3个腹板剪力占比相近，3个腹板承担的剪力约占截面总剪力的93%，且跨径的改变并不影响各腹板的剪力分担比例；弯箱梁中3个腹板分担的剪力差异明显，圆心角变化会造成内侧腹板分担剪力比例减小，外侧腹板分担剪力比例增大，但中腹板分担的剪力比例受圆心角影响并不明显。在圆心角为24.56°时，曲线箱梁在边跨跨中截面外侧腹板承担剪力比例最大约为内侧腹板的2.65倍，中腹板的1.45倍；在支点截面处时，外侧腹板承担剪力比例最大约为内侧腹板的1.5倍，中腹板的0.73倍，从跨中截面至支点截面，截面剪力主要由外腹板承担逐渐变化到由中腹板承担。曲线箱梁各控制截面的中腹板承担比例与同跨径直线桥梁一致，表明曲率对中腹板影响较小；但随圆心角的增大，中腹板的剪力承担比例逐渐增加，外侧腹板占比大于内侧的现象也逐渐明显，这表明在“弯扭耦合”作用下，腹板剪力分布随圆心角增大有逐渐径向向外转移的趋势，使位于的外侧腹板处于受力不利的情况。

由表2可知，式(3)、式(4)可进一步无量纲处理，图5给出了不同跨径下的剪力比值系数ξQ。

图5 剪力比值系数Fig.5 Shearing influence coefficient

如图5所示，在边跨跨中截面，圆心角大于8.73°时，剪力比值系数大于1.10，而当圆心角增大到24.56°时，剪力比值系数增加到1.44倍；在边跨支点截面，当圆心角为13.64°时，剪力比值系数为1.13，当圆心角增大到24.56°时，剪力比值系数也增加到1.22。

相同跨径下，曲线箱梁桥内侧腹板剪力相较与直线桥梁小，外侧大，且随圆心角增加差异变大；同时，曲线箱梁桥和直线箱梁桥的内力差异影响在跨中截面比支点截面大，这可能是因为支点处有较强的约束限制所致。

3.2 弯曲正应力分布差异分析

对于弯曲正应力，图6给出了一期恒载作用下同跨径(跨径45 m，圆心角为24.56°)直线箱梁桥和曲线箱梁桥在边跨跨中截面和边跨支点截面的顶板上缘、底板下缘弯曲正应力分布情况。从图6可知，曲线箱梁各控制截面的弯曲正应力分布不均匀现象更为明显，且在支点处应力分布不均匀现象比跨中处更加明显。

曲线箱梁桥存在内侧弧长比外侧短，在竖向荷载作用下梁体内不仅存在弯矩还会产生较大的扭矩，二者耦合作用导致曲线箱梁在边跨跨中截面弯曲正应力呈现“内大外小”的现象(图6)。但是，在曲线箱梁支点截面正应力则呈现“内小外大”的相反的分布规律，且内、外侧弯曲正应力均大于直线箱梁桥，这可能是因为曲线箱梁桥外侧竖向变形大于内侧变形，但限于支点截面的竖向约束，致使支点截面外侧弯曲正应力大于内侧。

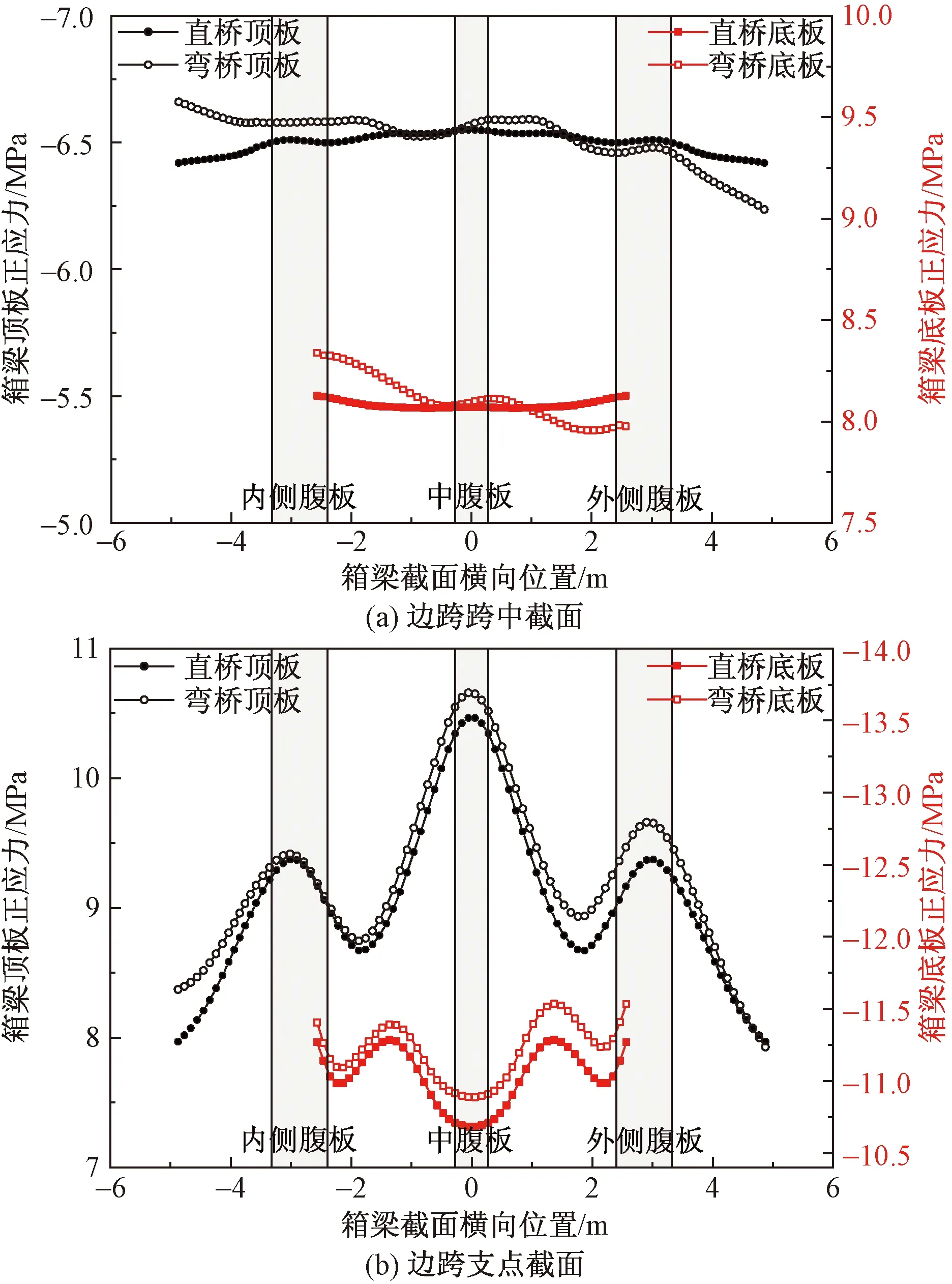
图6 边跨顶、底板纵向正应力分布Fig.6 Normal stress distribution of roof and floor

为定量描述在一期恒载作用下的应力分布不均匀现象，使用剪力滞系数λ来评价曲线箱梁桥的空间应力分析，剪力滞系数可定义为截面同一高度位置处最大正应力与平均正应力之比，可表示为

(5)

表3给出了在一期恒载作用下，跨径16 m(圆心角为8.73°)的直线箱梁桥和曲线箱梁桥各控制截面的剪力滞系数。从表3可知，顶板最大剪力滞系数为1.35，底板最大剪力滞系数为1.12；支点截面剪力滞系数大于跨中截面；但直桥箱梁桥与曲线箱梁桥在各控制截面的剪力滞系数差异不明显，在工程设计中可取同等跨径的直线箱梁桥剪力滞系数作为曲线箱梁桥的剪力滞系数进行设计计算。

表3 控制截面顶、底板剪力滞系数Table 3 Shear lag coefficient of roof and floor of control section

上述箱梁桥截面应力在同一高度位置存在不均匀现象，进一步应力差值和应力比值系数两个评价指标反应一期恒载作用下跨径改变(即圆心角)对曲线箱梁桥与同跨径直线箱梁桥的应力差异影响，应力差值可表示为

Δ=σC-σS

(6)

应力比值系数可表示为

(7)

式中：σC、σS分别为同跨径曲线箱梁桥和直线箱梁桥在箱梁顶、底板同一位置的正应力值。

图7、图8给出了不同跨径下曲线箱梁桥和直线箱梁桥的在箱梁截面同一位置的应力差值和应力比值。如图7、图8所示，曲线箱梁桥截面正应力相较于直线箱梁桥呈现“内大外小”的现象随着跨径增加愈发明显；在靠近中腹板偏内侧不远处，存在应力差值零点，这可能是弯扭耦合作用下，曲线箱梁桥受力重心向内侧偏移，箱梁截面同一高度位置应力出现向一侧“倾斜”的趋势，曲线箱梁桥中性轴不再水平，这与文献[12]中所述结论相似，表明基于平截面假定的杆系理论已不能真实的反应曲线箱梁桥的空间受力分布情况。

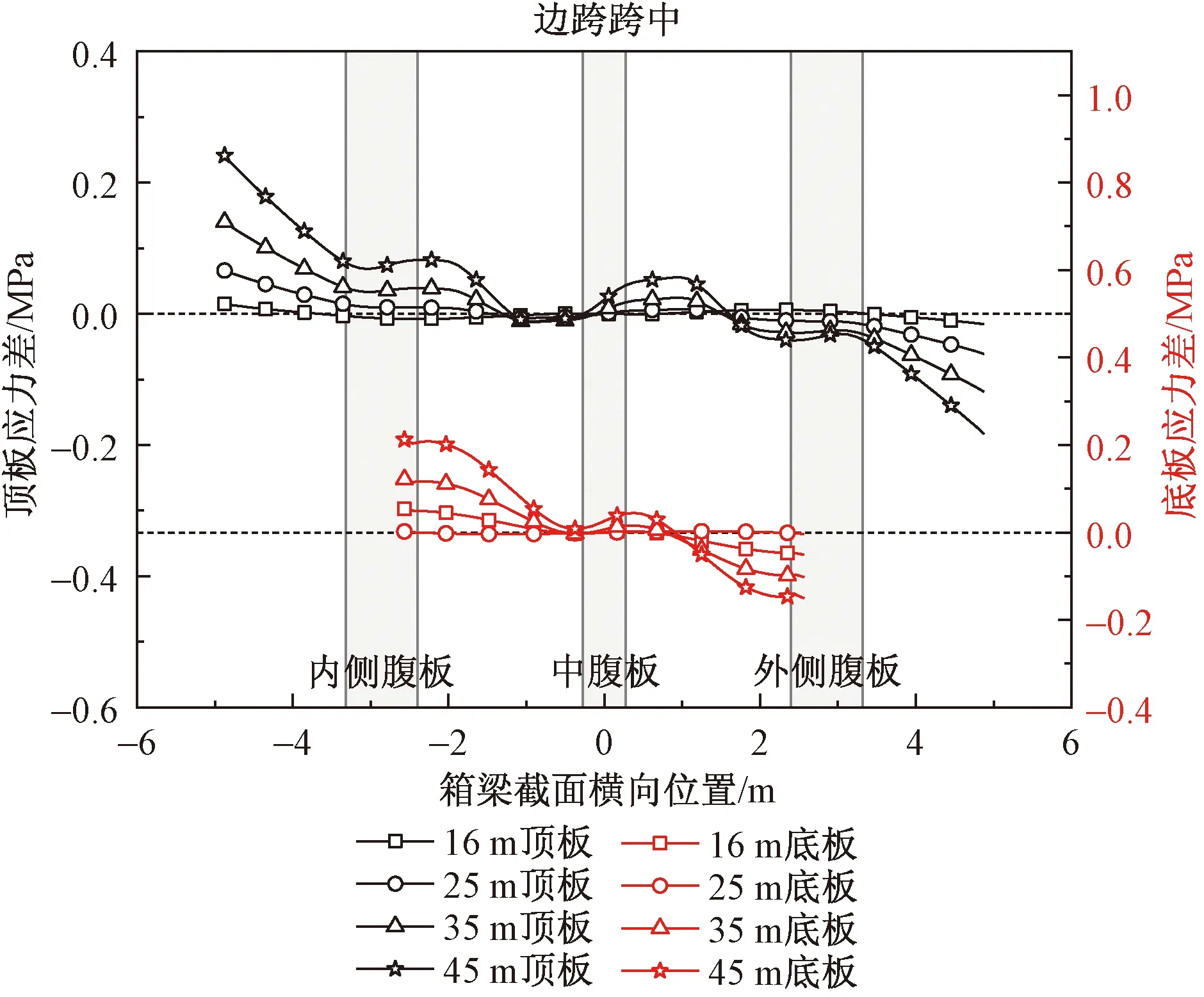
图7 应力差值Fig.7 Stress difference values

图8 应力比值Fig.8 Stress ratio

在圆心角为24.56°时，曲线箱梁桥在内侧翼缘板边缘节点弯曲正应力值比同跨径直线箱梁桥大0.24 MPa，比值约为直线箱梁桥的1.037倍；对应外侧翼缘板节点弯曲正应力比直线箱梁桥小0.18 MPa；底板底缘内侧节点应力差值为0.21 MPa，外侧为0.15 MPa；但在箱梁任意相同位置，曲线箱梁桥相比于直线箱梁桥的正应力比值均小于1.05。对于曲线箱梁设计配筋计算可以采用不均匀系数，按文献[17]取截面应力不均匀系数为1.05～1.20都是可行的，但在设计中应对曲线箱梁桥的两侧翼缘板的配筋计算引起重视。

4 结论

通过ANSYS实体有限元法的计算，对不同跨径下曲线箱梁桥和直线箱梁桥的受力特点进行对比分析，得出以下结论。

(1)曲线箱梁桥与直线箱梁桥的截面总剪力值的差异不大，但在内、外侧腹板剪力分布上存在明显差异，曲线箱梁桥外侧腹板剪力值最大约为内侧腹板的2.65倍；当圆心角超过8°时，曲线箱梁边跨跨中截面外侧腹板的剪力已经超过同跨径直线箱梁桥的1.1倍；在边跨支点截面，当圆心角超过13°时，曲线箱梁外侧腹板的剪力已经超过同跨径直线箱梁桥的1.13倍；但是曲梁的圆心角对中腹板区域的影响不大，对外侧腹板区域受力不利，内侧有利。

(2)曲线箱梁桥与同跨径直梁桥的截面总弯矩值和剪力滞系数差异并不明显，可采用直线桥的剪力滞系数作为曲线桥的剪力滞系数进行计算；但是曲线箱梁的截面中性轴不再保持水平，同一高度处弯曲正应力呈现出向一侧“倾斜”的趋势，截面正应力呈现出由跨中截面“内大外小”向支点截面“内小外大”变化趋势。

(3)基于平截面假定计算的结果不能准确求解曲线箱梁的截面应力，在设计配筋时，应注意曲线箱梁桥内侧腹板剪力卸载效应；跨中截面外侧顶、底板正应力卸载，支点截面内侧顶底板正应力卸载的特性。