一类具有位势的二维非线性薛定谔系统解的渐近行为

马瑞， 李春花

( 延边大学 理学院， 吉林 延吉 133002 )

0 引言

本文考虑如下具有位势的非线性薛定谔系统的初值问题：

(1)

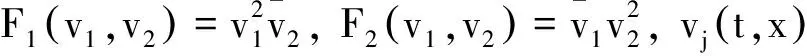
(2)

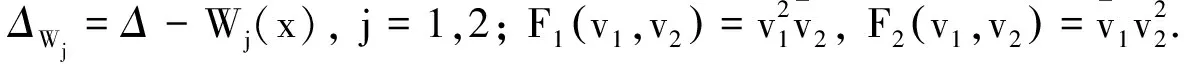
(H1)m1=m2；

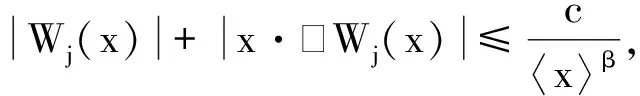
(H3)Wj(x)是非负的；

(H4) 零是一个正则点[1].

当Wj(x)≡0，j=1,2时，初值问题(2)可转化为：

(3)

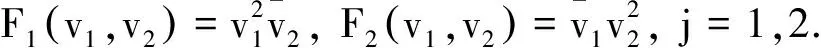
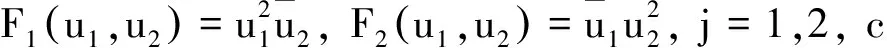
非线性薛定谔方程在非线性光学、等离子物理等领域均有重要的应用.近年来,带有位势函数的非线性薛定谔方程初值问题解的渐近性质受到学者们的广泛关注,并获得了一些结果[3-4]；但对带有位势函数的二维非线性薛定谔方程初值问题解的渐近性质研究得较少.文献[1]的作者仅研究了不含粒子质量、带有位势函数的二维非线性薛定谔方程初值问题.本文在系统质量共振的条件(H1)下证明薛定谔系统的初值问题(2)整体解的存在性，并讨论解的长时间渐近行为.

本文中向量函数空间和标量函数空间使用相同的符号.对任意的1≤p≤∞，Lp表示R2上关于勒贝格测度的p方可积函数空间， ‖‖Lp表示Lp上的范数.对任意m,s∈R， 定义加权索伯列夫空间Hm,s如下：

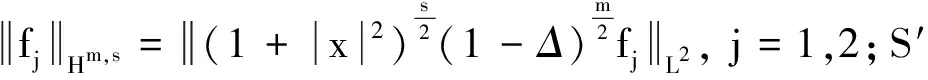
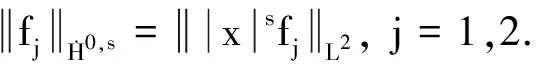
1 预备知识

首先定义

再令Uα(t)=F-1E(t)αF , 其中Ff是f的Fourier变换， F-1g是g的Fourier的逆变换，α≠0.则当t≠0时，Uα(t)和Uα(-t)可分别写成如下形式：

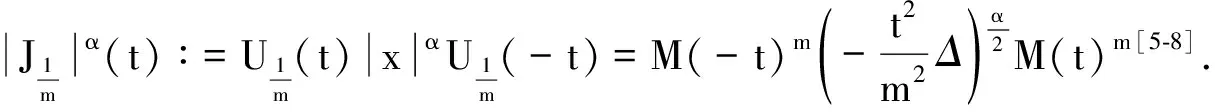
令[E,F]=EF-FE，并考虑如下两个引理：

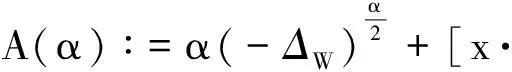
引理2设W(x)是R2上的实值函数，m∈R+， 0<α<2.令U∶=2W+(x·∇W)， 则下式成立：

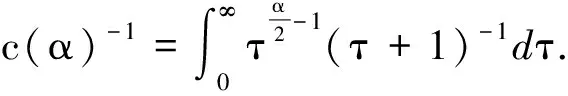
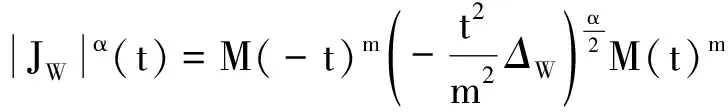
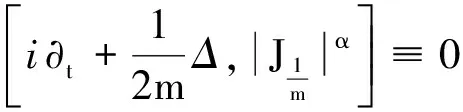
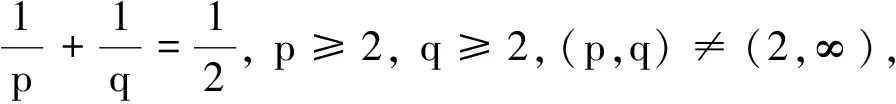
引理3[1]设W(x)满足条件(H2)—(H4).令a,b∈R,C是一个正常数， (p,q)和(r,k)是薛定谔容许对，则可以得到：

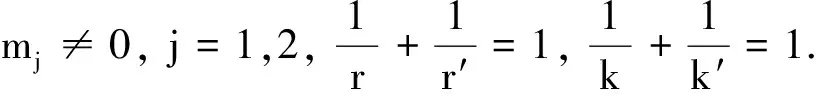
引理4[1]设W(x)满足条件(H2)和(H3)，C是一个正常数，则可以得到如下估计：

(i)对于任意的1≤α<2, 0<σ<1， 有

(4)

(ii)对于任意的α≥0， 有

(5)

(iii)对于任意的1<α<2， 有

(6)

引理5设系统(2)满足质量共振条件(H1)，Wj(x),j=1,2满足条件(H2)和(H3)，C是一个正常数，则有：

(7)

(8)

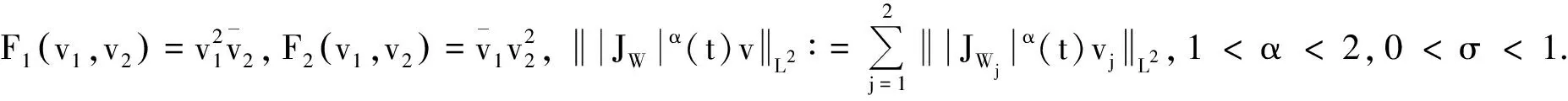
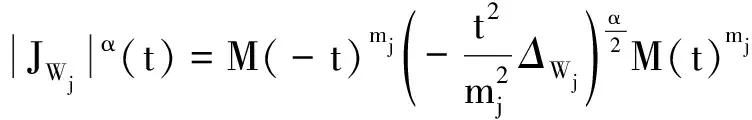
在上式的基础上，应用引理4中的式(4)、式(6)以及条件(H1)可得：

(9)

其中1<α<2， 0<σ<1.为了方便引理5的以下证明，定义

(10)

则应用式(5)、(6)、(9)和式(10)可得：

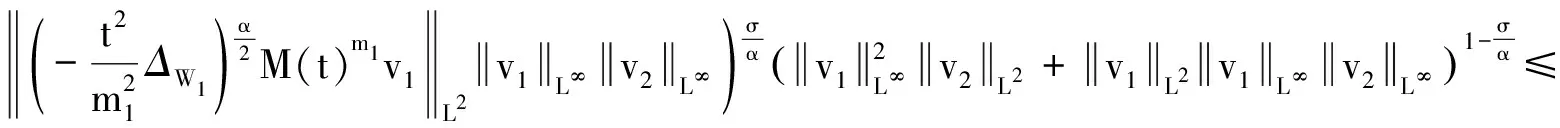
其中1<α<2， 0<σ<1.由以上知式(7)成立.通过类似的方法可得式(8)成立.证毕.

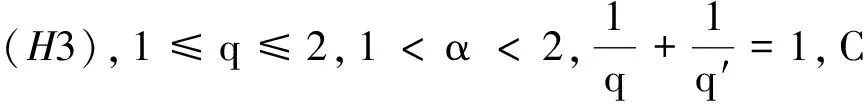
2 主要结果及其证明

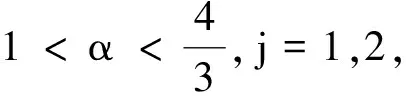
(11)

(12)

证明定义如下的函数空间：

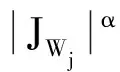
由上式可得：

(13)

根据引理3和式(13)有：

(14)

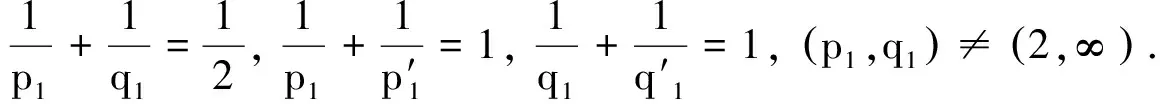
(15)

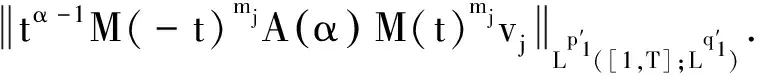
(16)

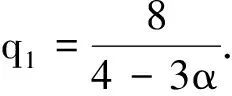
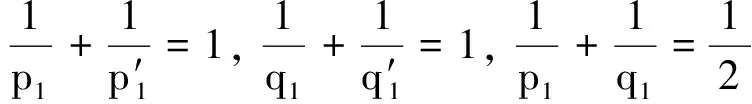
(17)

由式(7)、(8)、(14)和式(17)可得:

(18)

再由式(10)、(18)可得:

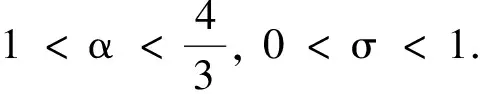
(19)

应用类似上述的方法，可以找到常数C2>0， 使得

(20)

基于上述应用Strichartz估计和类似初值问题(2)整体解衰减估计的证明即可得式(12)成立.证毕.