距离判别分析法在产品质量控制中的应用

欧阳娜， 黄利文

( 1.黎明职业大学 新材料与鞋服工程学院；2.泉州师范学院 数学与计算机科学学院: 福建 泉州 362000 )

0 引言

质量控制方法在提高企业的产品质量和竞争力方面具有重要的意义.目前，质量控制方法主要采用的是基于统计过程控制(statistical process control, SPC)的方法.SPC方法虽然可有效提高产品合格率，降低生产成本，但其仅适用于单个观测变量的过程监控，且其过程监控图缺乏统一的分析规则.为了克服SPC方法存在的上述问题，一些学者对SPC方法进行了改进或提出了新的一些质量控制方法.Hajej等[1]在SPC方法的基础上完善了单个变量过程监控的方法，提出了一种集成生产、维护和质量控制的监控策略，并通过数值算例验证了所提策略的有效性.Pimenta等[2]针对观测数据存在自相关的问题，将自回归模型、多元统计、自相关、多重共线性等方法引入到质量监控中，研究结果显示该方法可有效提高产品质量.Viharos等[3]将强化学习引入到SPC方法中，结果显示该方法可有效提高产品质量.Ranaee等[4]提出了一种混合的智能识别控制图模式(CCP)，仿真结果显示该模式识别异常问题的正确率约为99.37%.Bersimis等[5]基于多元统计方法探讨了多个观测变量的过程监控问题，扩展了单变量过程监控的方法.上述研究虽然改善了SPC方法的一些过程监控问题，但在产品质量等级划分方面还存在不足.为能更好地解决多个观测指标的质量控制问题，本文提出了一种距离判别分析方法，并通过仿真实验验证了本文方法的有效性.

1 多个观测指标的质量控制理论基础

设某一产品的生产过程包含k(k>0)道工序，k中有m个观测指标X1,X2,…,Xm， 其中Xi的均值记为μi， 标准差记为σi，i=1,2,…,m.

在1个观测指标的SPC的质量控制中，通常采用六西格玛原则来控制产品的质量.一般是将观测数据位于区间(-σ,σ)的产品设定为质量最好，将位于区间(-2σ,2σ)(-σ,σ)的产品设定为质量一般，将位于区间(-3σ,3σ)(-2σ,2σ)的产品设定为质量较差，不在上述3个区间的产品属于不合格产品.由以上可知，不同质量产品的观测数据具有包含关系的特点.在多个观测指标的质量控制中，由于产品在生产过程中具有多重不确定性因素，因此会使观测数据变得更加复杂.

在产品的质量类别中，G1表示质量最好的合格产品类别，G2表示质量一般的合格产品类别，G3表示质量较差的合格产品类别，G4表示质量不合格的产品类别.不同产品类别的数据关系见图1.

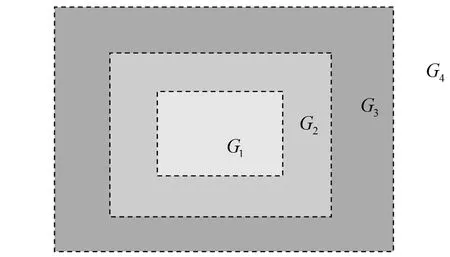
图1 不同产品类别的数据关系

由图1可知，多观测变量的质量监控数据具有一环包围一环的特点.目前，判断多个观测指标的质量控制数据一般采用判别分析方法、支持向量机(support vector machine, SVM)、集成分类(ensemble classifiers, EC)方法和K最近邻分类(K- nearest neighbor, KNN)方法.由于传统的判别分析方法针对一环包围一环的数据集时易出现误判的情形，因此一些学者对该方法进行了改进.例如：文献[6]在传统的判别分析方法的基础上探讨了混合球状数据的判别问题，但由于多个观测指标的质量控制数据不一定是球状数据，因此该方法在应用上具有一定的局限性.Huang等[7-8]对文献[6]提出的方法进行了改进，这些方法虽可提高非球状数据集的判别正确率，但不易分析样品的误判原因.SVM是一种应用较广的分类方法，具有较高的分类正确率[9-11]，但该方法用于多个观测指标的产品质量等级分类问题并不稳定.EC[12-14]和KNN[15-16]方法具有较好的稳定性和分类效果，但难以分析对产品的误判原因.为了更好地区分产品质量所属的类别和分析影响产品质量的因素，本文在SPC的基础上提出一种改进的距离判别分析方法.首先引入如下定义：

性质1d(x,Gp)是无量纲的.

性质2 若x∈Gp， 有0≤d(x,Gp)≤1.

性质3 对任一样品x，有：

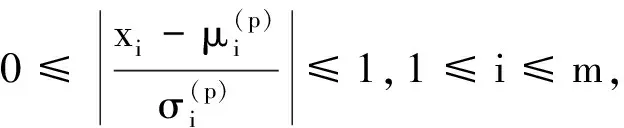
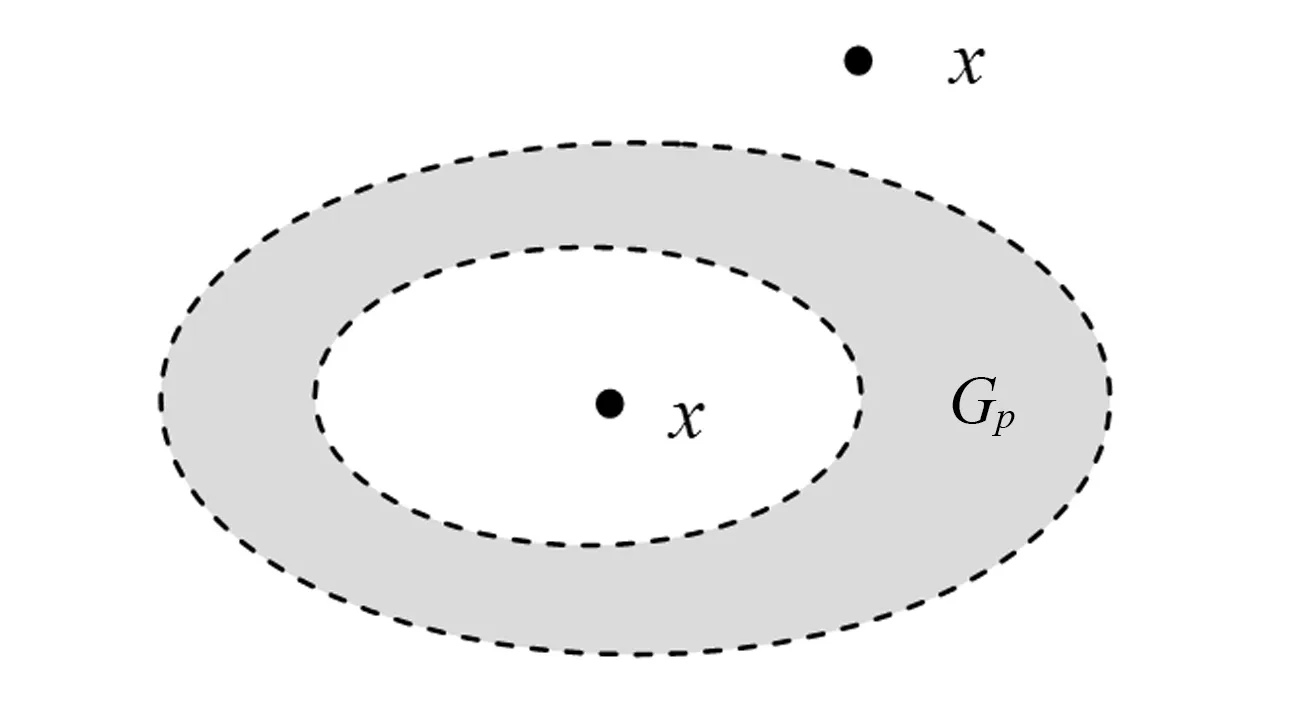
图2 x与Gp的关系

由于有时难以获得不合格成品的数据，因此无法直接判断成品是否属于不合格产品.解决这个问题的思路有两种：一是采用蒙特卡罗方法模拟不合格产品的数据，然后通过这些数据判别产品是否合格；二是通过G1、G2、G3的质量等级间接判别产品是否合格.为了方便起见，文中采用第2种思路对产品进行质量控制和等级分类.

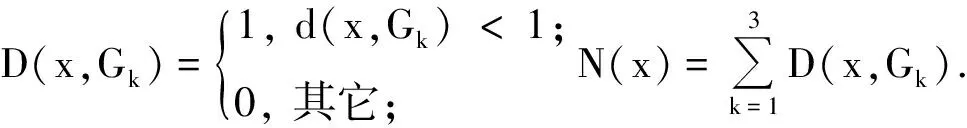
2 距离判别分析法在产品质量控制中的应用

2.1 产品质量控制流程

在SPC方法的基础上建立的产品质量控制体系的产品质量控制流程如图3所示.

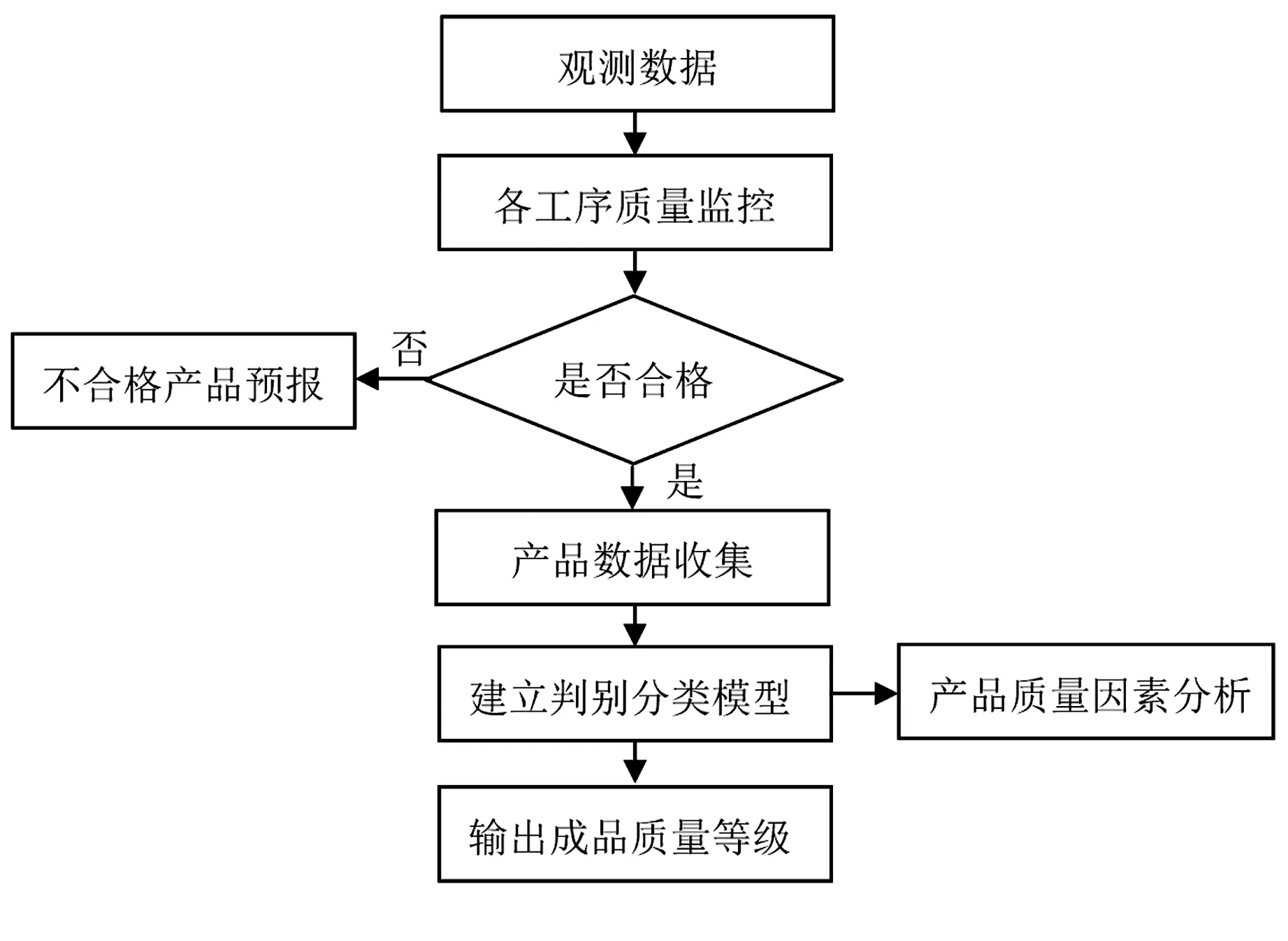
图3 产品质量控制流程

2.2 产品质量控制过程监控

在SPC方法的产品质量控制过程中，常用控制图中的点的分布和趋势来评估生产过程的情况；但由于对制图缺乏统一的分析规则，因此不同人对图的分析结果存在较大差异[17].为了克服这一问题，本文利用上述N(x)建立一种新的产品质量过程监控图，见图4.由图可知，当N(x)=1时，产品的质量为最好； 当N(x)=2时，产品的质量为一般；N(x)=3时，产品的质量为较差； 当N(x)=0时，产品的质量为不合格.

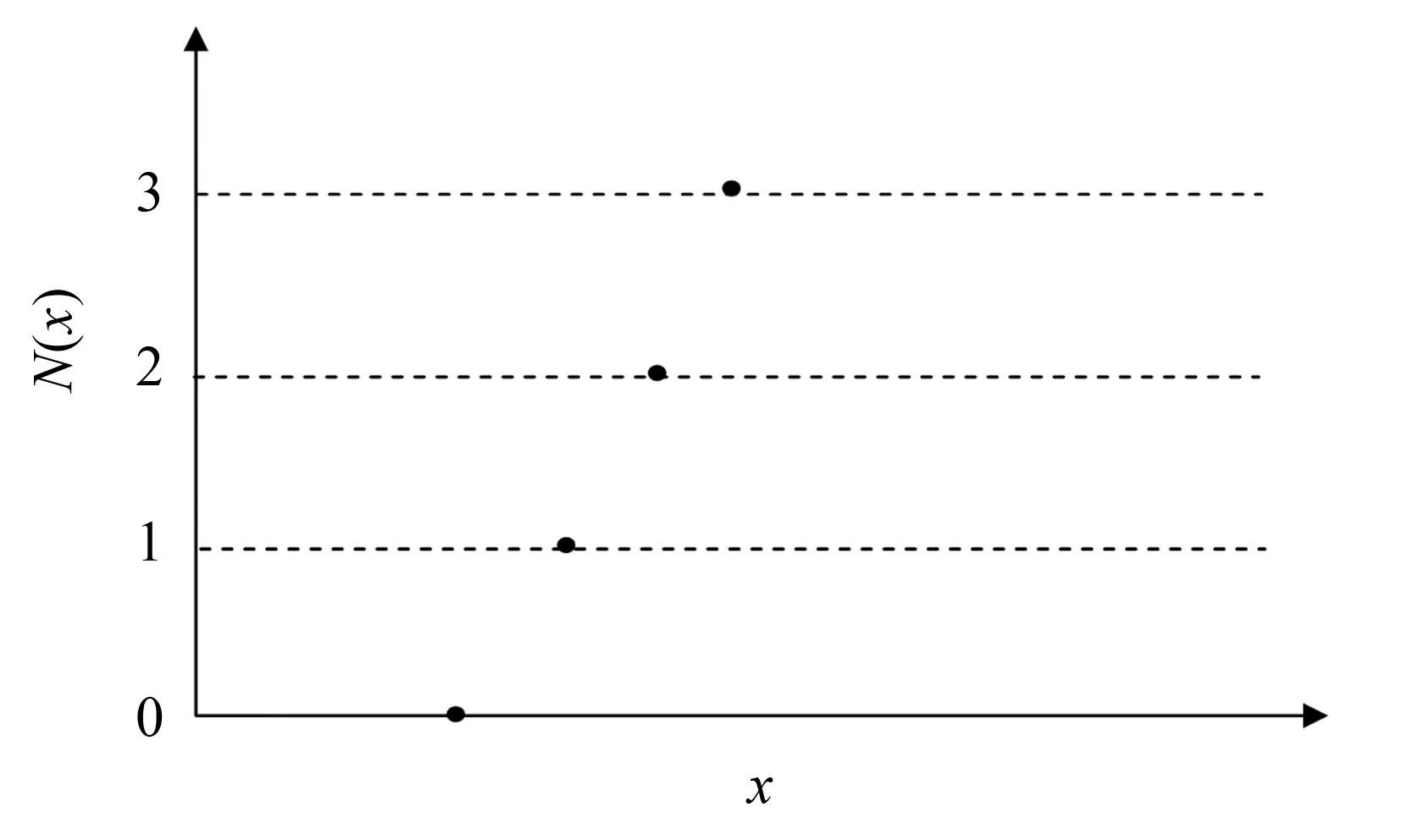
图4 产品质量控制过程监控图

由2.1中的产品质量等级判别分类模型可以得到产品质量等级的相关数据.根据这些数据得到的各产品的质量等级如图5所示.由图5可知，利用该图即可了解产品生产的质量情况.

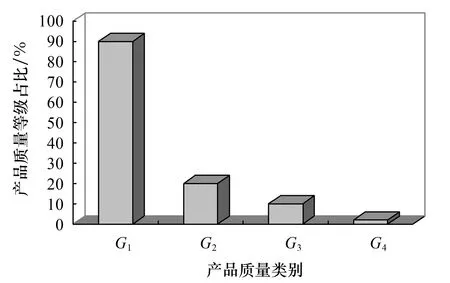
图5 不同产品的质量等级占比

2.3 影响产品质量的因素分析

为了解观测指标Xj所确定的Gi样品数量，本文引入变量Nij， 其表达式为：

其中1≤i≤4， 1≤j≤m.于是有

(1)

记第j个观测指标属于第i个质量等级的比例为Rij， 其计算公式为：

(2)

其中1≤i≤n， 1≤j≤m.根据式(1)和式(2)计算得到的产品质量的观测指标见表1.

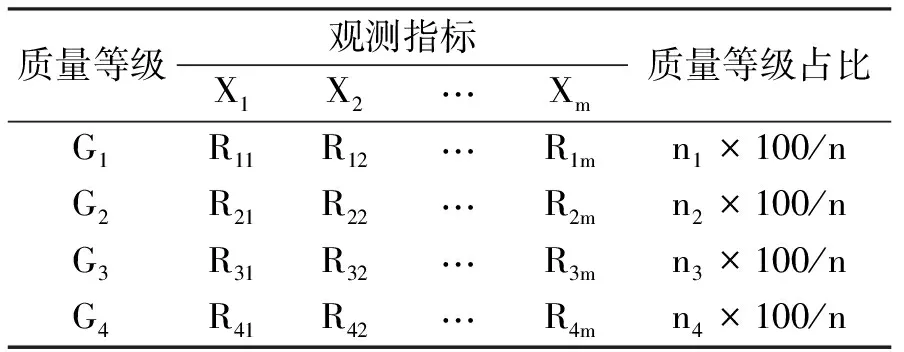
表1 产品质量观测指标分析表 %

在表1中，当j固定时，一般有R1j>R2j>R3j>R4j， 1≤j≤m.若R1j、R2j、R3j、R4j不是依次递减时，则需分析该现象的出现原因，如机器故障、人为因素、原材料问题等.此外，若产品合格率不符合实际要求时，可通过对Rij值进行分析来发现引起产品质量下降的因素，从而及时采取相应维护措施.

3 仿真实验

通过模拟产品的生产过程对本文提出方法的有效性进行仿真实验.设某一产品生产有3道工序：第1道工序有2个观测指标，记为X1和X2； 第2道工序有1个观测指标，记为X3； 第3道工序有2个观测指标，记为X4和X5.5个观测指标的均值和标准差如表2所示.产品质量控制的仿真实验设置为3种，每种方案的G1、G2、G3、G4的产品数量各不相同(见表3).产品数据(10 000个)采用蒙特卡罗方法模拟.

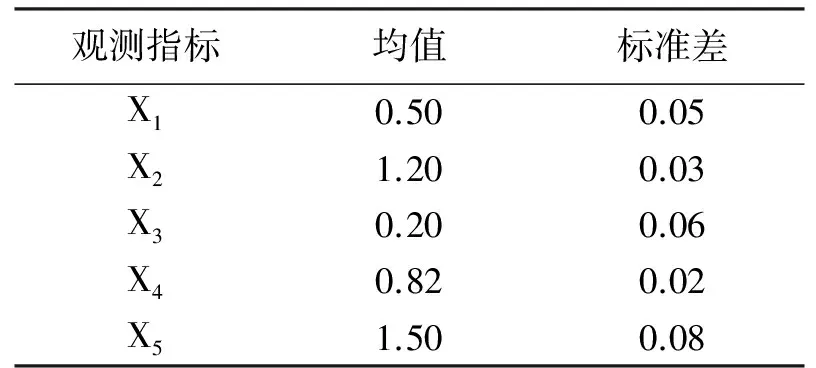
表2 产品观测指标的均值和标准差

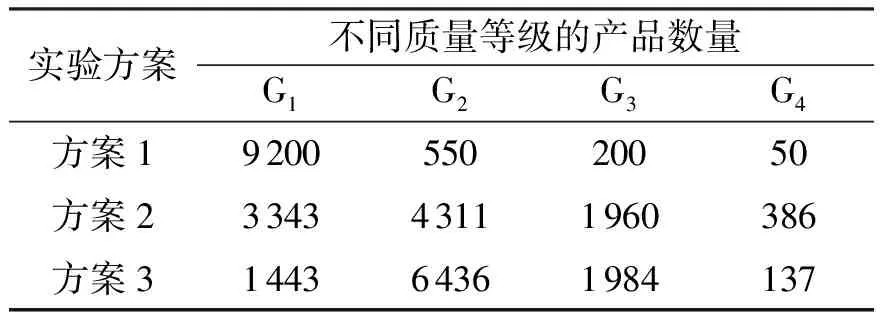
表3 各实验方案不同质量等级的产品数量

采用本文的方法对表3的3种方案进行质量监控和等级分类，并与Fisher判别分析法(FLDA)、贝叶斯判别法(BSDA)、马氏距离判别法(MDA)、KNN方法、EC方法和Monte Carlo方法进行比较，结果见表4—表5.由表4可以看出，本文方法和KNN方法的分类正确率达到100%，显著优于FLDA、BSDA、MDA、EC方法的分类正确率.其原因是多观测变量的产品质量观测数据是一环包围一环的，且数据不平衡，因此导致传统的判别分析方法和EC方法的效果不佳.另外，当产品的合格率较低时，EC和KNN分类法无法从观测数据中分析影响产品质量的因素.由表5可以看出，Monte Carlo方法对不同模拟数据的分类正确率均达到96%以上，表明该方法具有良好的稳定性；但该方法分类的正确率与总体G4的模拟数据密切相关，当G4的样本数据按各个观测变量标准差的7倍(或7倍以上)进行模拟时，其分类正确率才可达到100%.由以上可知，本文的方法在质量监控中具有较好的效果.

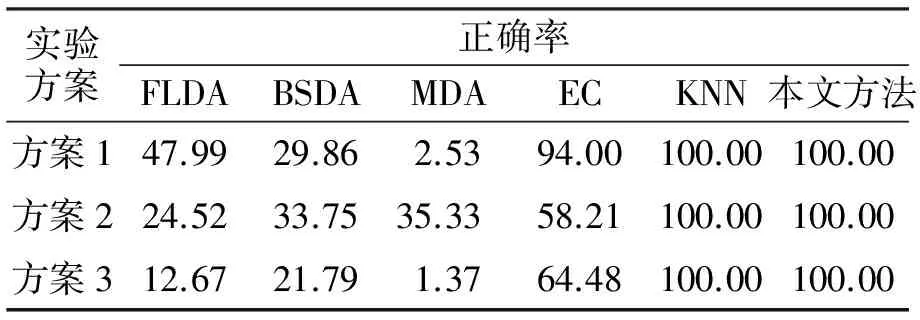
表4 不同判别方法的正确率 %

表5 Monte Carlo方法运行100次的平均测定结果 %

依据2.3中的分析得到的3种方案的产品质量分析表见表6—表8.从SPC的监控方法来看，3种方案的产品合格率均较高(方案1的产品合格率为99.50%，方案2的产品合格率为96.14%，方案3的产品合格率为98.63%)，但采用SPC方法无法了解产品的质量等级情况；而本文的方法不仅能了解产品的合格率和产品的质量等级情况，还能够通过产品的质量分析表分析产品的生产过程是否出现异常.例如：由表6可以看出，方案1中G1、G2、G3和G4的占比分别为92.00%、5.50%、2.00%、0.50%，其中质量最优的合格产品占比最大，其余的质量等级占比很小且依次递减，这表明方案1的产品生产状态较好.由表7可以看出，方案2中G1、G2、G3和G4的占比分别为33.43%、43.11%、19.60%、3.86%，其中一般的合格产品占比最大；另外，还可以看出表中的第2个观测变量出现异常，因此需对第2个观测指标所对应的机器进行检查和维修等，以提高产品质量.由表8可以看出，方案3中G1、G2、G3和G4的占比分别为14.43%、64.36%、19.84%、1.37%，其中一般的合格产品占比最大；但由于各个观测变量所确定的质量等级无明显差异，因此需要对整个生产流程进行检查和改进以提高产品质量.

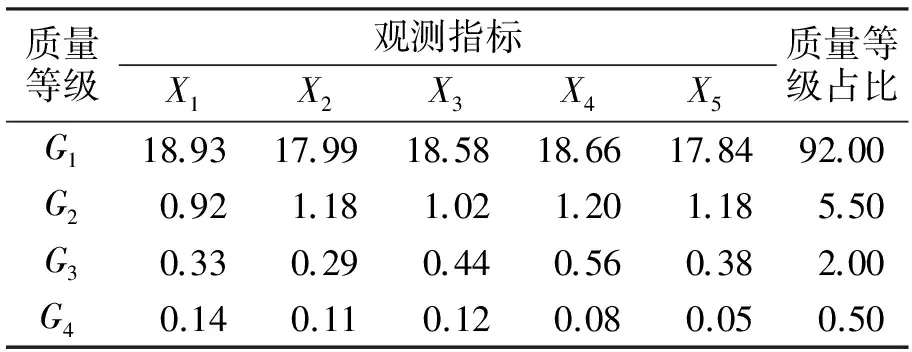
表6 方案1的产品质量分析表 %

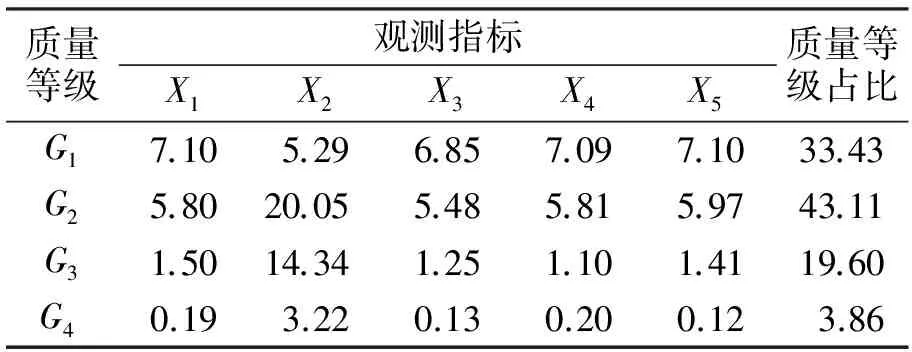
表7 方案2的产品质量分析表 %

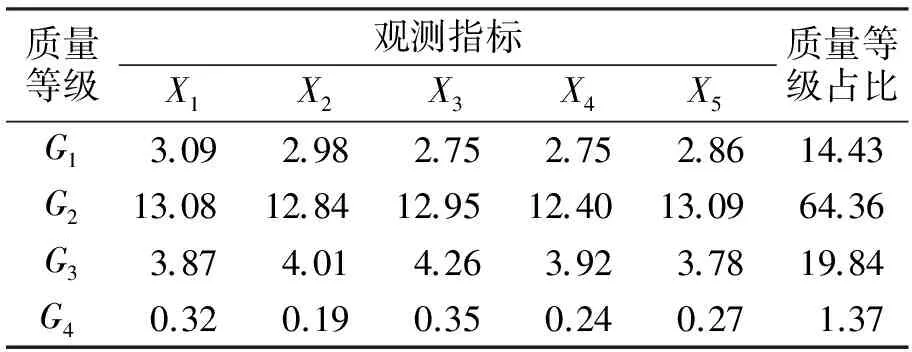
表8 方案3的产品质量分析表 %

4 结论

仿真实验结果表明，本文提出的质量监控方法的过程监控图不仅具有简单、直观的优点，而且还具有统一的分析规则，可消除SPC方法过程监控图中的“标准分析问题”；同时，该方法能够对SPC方法中产品质量等级进行分类，且分类准确率达到100%.另外，通过产品质量分析表还能够较好地了解成品的质量等级情形和各个观测指标是否出现异常，进而对产品的生产过程起到质量监控作用.本文在研究中仅涉及到了产品生产过程中的质量控制方面，而对机器寿命、客户对产品的需求变化等方面没有进行探讨，因此今后我们将进一步探讨解决多个观测指标的质量控制问题，以提高本文方法的适用性.