“读思达”导向下小学数学空间观念培养的有效途径

崔玉兰

（福建省莆田市第二实验小学，福建莆田 351100）

引 言

空间观念是学生必须掌握的关键能力之一，它的本质是空间想象力，它的形成是一个循序渐进的过程。结合实际教学经验，笔者就如何在教学中培养和发展学生的空间观念进行了分析，并总结出三大有效途径。

一、问题导向启阅读

《义务教育数学课程标准（2011年版）》把“图形与几何”领域的内容分为四个部分，即图形的认识、测量、图形的运动、图形与位置，每个部分都是从多角度刻画几何图形，包括图形的特征、图形的大小、图形的运动和图形的位置，且都有丰富的插图。人教版教材（教材版本下同）在图形的认识部分，按照“立体—平面—立体”的顺序来安排教学内容，实现从“三维—二维—一维—二维—三维”之间的不断转化。教师要领会课本中每幅图的意图，以指导学生有效阅读。

例如，在教学一年级下册的“认识图形（二）”一课时，教师可以先出示主题图，引导学生带着问题边读边思考。比如，教师可以提出问题：“图上的小朋友手里拿着什么？他们又在做什么呢？你想不想动手试试？”学生带着问题读图，能够在边读边想中初步感悟立体图形与平面图形的关系，通过描、画、印、拓等方式抽象出长方形、正方形、三角形、圆等平面图形。这样的教学方式既能渗透平面图形与立体图形的关系，又能使学生感受到“面在体上”。在学生画出不同的平面图形后，教师可以引导学生再读图并思考：“这些不同的图形该怎么分类？这些形状、大小都不同的图形为什么都是长方形？”在释疑解惑中，学生能够从个别到一般，从单一到丰富，初步建立平面图形的表象特征。随后，教师可以引导学生第三次读图思考：“这些长方形在哪种立体图形的面上？几个长方形可以拼成一个长方体？正方形、平行四边形、三角形及圆形呢？”第三次让学生读图并进行逆思考。在学生想象后，教师可以利用多媒体设备动态演示长方体的形成过程，用平面图形构建立体图形，引导学生再次体会点动成线、线动成面、面动成体的过程。

这样进行平面图形与立体图形的转化，建立面和体的联系，从横向数学化到纵向数学化，能够帮助学生完善认识，形成空间表象，培养空间观念。

二、动手实践与思考相结合

儿童心理学家皮亚杰说过：“思维是从动作开始的，切断了动作与思维的联系，思维就得不到发展。”儿童的空间观念是在有效的教学活动中发生、发展的[1]。在教学中，教师要善于抓住时机，让学生多感官参与实践活动，并与数学思维活动有机结合起来，边操作边思考，从而积累活动经验，构建空间表象。

例如，在教学二年级上册“角的认识”一课时，为帮助学生构建角的概念，教师可以设计三个层次的动手实践与思考相结合的活动。（1）先实践体验再思考。教师可以先让学生在教室里看一看、找一找、指一指，找出有角的物体，让学生对角的特征有更直观的认识；然后，让学生说一说这些角长得一样吗，它们有什么相同的地方。（2）先思考再实践。在学生初步认识角的特征后，在比较两个角的大小时，教师可以让学生先猜测再动手验证。基于学生原有的经验和认知，教师应鼓励学生猜测，再让学生通过操作验证自己的猜测，从而调整原有的教学方式，有效培养学生的空间观念。（3）实践、思考后的再思考。在学生画角的基础上，教师可以展示学生作品，先让画对的学生分享自己成功的经验，引导其说出画角时要先画一个顶点，再用尺子朝不同的方向画两条直边；然后，让学生对错误作品展开讨论，使学生在对话与交流中深刻体会角的特点及正确的画法。这样的教学方法能使学生亲身经历活动的过程，获得直观体验，有利于他们进行正确的抽象与概括，从多角度认识角，理解与掌握角的特征，进而强化他们的空间观念。

又如，在“圆锥的体积”一课中，以往教师通常围绕圆锥体积和与它等底等高的圆柱体积的关系开展教学，教学效果往往不尽如人意，因为学生在计算圆锥的体积时经常漏掉1/3。为此，教师可以改变教学策略，在教学时将学生分成不同的学习小组，为每组学生提供2个圆柱、2个圆锥的容器，还有沙子和水等学具，让学生按要求动手操作实验。学生通过动手操作发现：四个容器中，如果将等底等高的圆柱和圆锥分到一组进行实验，圆锥盛三次水或沙才能把圆柱装满；如果按不相等的底和高分成两组，就不是倒三次才能倒满。这样，在实践中思考并对比，学生能够深刻体会到圆柱和圆锥在什么关系下才符合“圆锥体积是圆柱体积的1/3”这一规律，从而发现规律、建构模型。这样的实践体验与思考相结合的教学方式，能够促使学生更深刻地理解圆柱和圆锥的体积关系，在丰富的体验中培养空间观念。

三、留有充分的想象与表达空间

留给学生充分的想象和表达空间是培养学生空间观念的有效途径[2]。在教学中，教师可以引导学生借助身边实物进行想象，也可以让学生根据语言表达进行想象，还可以让学生通过动手操作、直观图进行想象。总之，教师要引导学生建立“形”与“体”之间可逆的转换关系，在生活原型、几何图形与它们的名称、特征之间建立起可逆的认知结构，实现“二维”与“三维”的转换。

比如，学生看到教室的黑板、课桌的桌面等实物，就会联想到长方形，在头脑里再现图形，想到长方形对边相等、四个角都是直角；看到胸前的红领巾马上就能联想到它的形状是三角形，想到它有三条边、三个角，而且还是等腰三角形，两个底角相等；等等。这样通过想象来完成“形”与“体”的转换，能切实加深学生对所学知识的理解。在平时教学中，教师要有意识地挖掘可利用的素材进行教学设计，据此培养学生的空间观念。

在教学中，教师可以引导学生根据数据、文字、语言表达等进行想象[3]。例如，传统教学中，在讲解“长方体认识”的相关内容时，教师往往只注重对面、棱、顶点的讲解，却忽视了面与棱之间的关系。而在“读思达”导向下，教师可以设计如下练习：下面有8个长方形（见图1），哪几个能围成一个长方体？

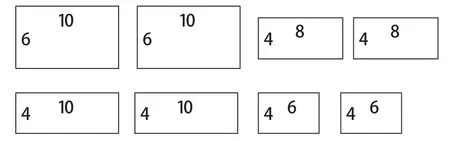
图1

在选择图片时，学生必须在头脑中完成把六个长方形拼成长方体这一想象过程。学生在长方体的立体图与展开图之间进行转换和想象并表达出来，不仅能够加深对面与棱的特征的认识，还能够培养推理归纳能力与表达能力。

又如，在教学“方向与位置”一课时，教师可以让学生通过想象画出路线图，再用语言描述行走的路线，从而培养学生的空间观念。

结 语

综上所述，充分阅读并挖掘素材、动手实践与思考相结合、留有充分的想象与表达空间是培养学生空间观念的三大有效途径。在数学教学中，教师要调动学生多感官参与活动，使其积累丰富的感性经验，促使其对几何体形成深刻的认识，从而有效培育养学生的空间观念，提升学生的数学学科核心素养。