蜘蛛机器人梯度投影法的运动分析和仿真

唐 军，秦 智，杨书麟

（江西理工大学机电工程学院，江西 赣州 341000）

1 引言

仿生机器人功能强大、可靠性高、应用广泛，使得该领域成为中国制造2025关注的热点。因爬行类机器人具有独立的支撑点而使得爬行机器人的机动性、可靠性比轮式或履带式机器人高，在恶劣环境中四足机器人可以代替人类开展救灾、灭火、核辐射区救援等专项工作。因此，对仿生足式机器人的运动和控制研究，具有较强的现实意义[1]。

20 世纪60 年代初，国外科学家开始致力于腿式结构机器人的研究，文献[2]研制出两自由度简单对角线爬行的“Phoney pony”机器人。随后文献[3]仿照哺乳动物研制出简单机械结构的四足机器人，文献[4]公司的研究人员开发出在崎岖道路快速行走的可承载较高载荷的四足步行机器人[5]。国内，文献[6]开发了伺服电机驱动的三自由度机器人JTUWM-III；文献[7]开发了TIM1 仿哺乳动物四足机器人；文献[8]研制了电力驱动大型四足机器人。但是，以上研究和开发的四足机器人体积庞大、惯性大、控制困难[9-12]。针对以上问题，这里设计了一款惯性小、体积小、移动可靠、易于控制的仿生四足机器人。当它运动时，足部运动的控制精度成为判定机器人性能的关键，而机身各关节的角位移、转矩、接触力是躯体控制的关键点。因此，通过机器人关节变量和运动轨迹的关系进行仿真模拟，找出爬行四足机器人的控制方程，并利用梯度投影算法求解，验证设计结构的合理性。

2 蜘蛛类生物结构及运动特性

昆虫种类繁多，不同的昆虫身体构造和运动方式有明显差异，以蜘蛛类昆虫为例，其身体构造，如图1所示。

图1 蜘蛛结构图Fig.1 Spider Structure

蜘蛛每条腿的结构分布相似，均由六个关节组成，六个关节依次为端附节、基附节、胫节、髌骨节、股骨节、转节。由于端附节、基附节、髌骨节的相对较短，胫节、股骨节、转节较长，这样可以使腿部运动更加灵活，在运动时能起到主导作用。蜘蛛类昆虫一般采取直线型的静态运动方式，运动时都采用腿部交叉的运动方式，第一步足、第三步足、第五步足运动，第二步足、第四步足、第六步足处于静止状态，结构上维持三角形来保持身体平衡。端附节、基附节、髌骨节以及爪的转动幅度较小，躯体运动主要通过胫节、股骨节、转节横摆转动，其余关节运动可忽略不计。

3 四足爬行机器人的结构分析

通过分析蜘蛛类昆虫的身体结构及运动方式可知，端附节、基附节、髌骨节转动幅度较小。为了方便机器人的关节设计，将转动较小的关节自由度去掉并对腿部数量进行选择，从而确定四足仿生机器人的单腿三自由度结构，四足爬虫机器人仿照蜘蛛运动机理，机器人腿部结构，如图2所示。将腿部结构分为三节式，转节、股骨节、胫节的连接采用正交连接方式，三关节采用舵机驱动模式实现绕轴旋转，实现三关节多角度运动。

图2 机器人腿部结构图Fig.2 Robot Leg Structure

四足爬虫机器人的结构原理图与模型图，如图3、图4所示。图3各条腿的转节用字母K1、K2、K3、K4表示，股骨节用字母X1、X2、X3、X4表示，胫节用字母H1、H2、H3、H4表示，腿尖用字母f1、f2、f3、f4表示，腿的具体编号用Leg1、Leg2、Leg3、Leg4 表示，转节K1旋转产生角位移推动股骨节产生位移，股骨节X1旋转产生一定角位移推动胫节的方位发生变化，胫节H1旋转改变f1的横向位移，转关节K1、股骨节X1、胫节H1的角位移量的矢量和构建出爬虫机器人单腿足尖f1的运动轨迹。Leg2机构各关节运动前后驱使机架产生角位移θ2，机身逆时针产生总角位移α，Leg3机构前后共产生角位移-α驱使机身顺时针偏转，机身结构竖直方向相对之前位置前进位移l，因此，机身前进位移l为四足爬虫机器人的单元摆动前进位移。四足爬虫步态规划简图，如图5所示。

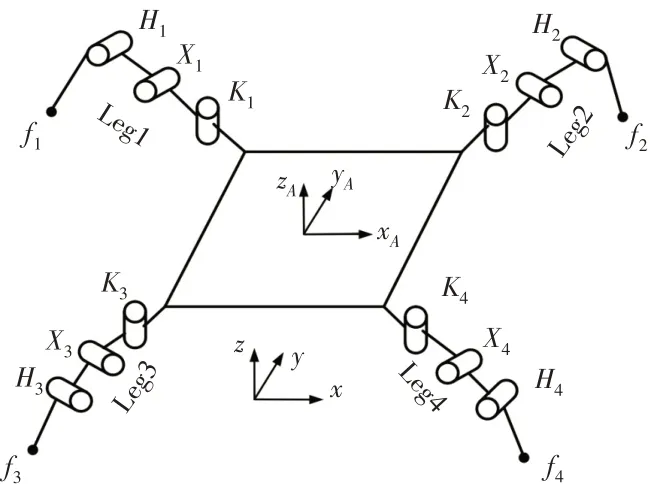
图3 机器人结构图Fig.3 Robot Structure Diagram

图4 爬虫机器人Fig.4 Reptile Robot

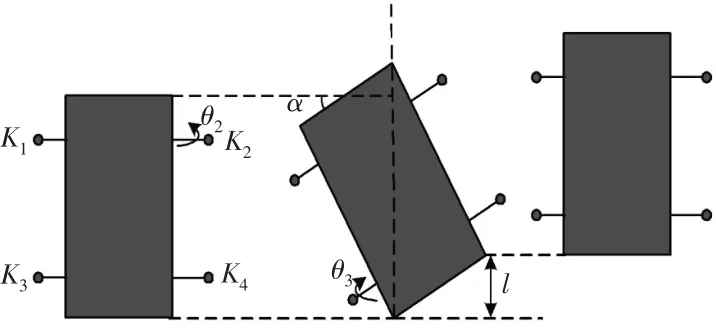
图5 机器人步态规划简图Fig.5 Robot Gait Planning Sketch

4 运动学模型的建立

4.1 单腿MDH运动方程建立

为了便于对机器人足部轨迹研究控制和关节分析，可将机器人的各个关节的衔接处的长度忽略不计，利用MDH方法（modified Denavit-Hartenberg）建立机器人运动学方程，即机器人的腿部MDH 模型。腿部MDH 模型，如图6 所示。对机器人左前腿（FL）建立关节坐标系。

图6 机器人的腿部机构MDH坐标系Fig.6 Robot Leg Mechanism MDH Coordinate System

机器人左前腿的结构参数，如表1所示。基于MDH模型在扭角αi-1、连杆长度ai-1、偏距di、关节角θi，为了解决D-H法仅能应用于两轴近乎平行的缺陷，引入附加转动项Rot（y，βi）来修正关节坐标系变换引起的偏差。机器人腿部关节变换矩阵为：

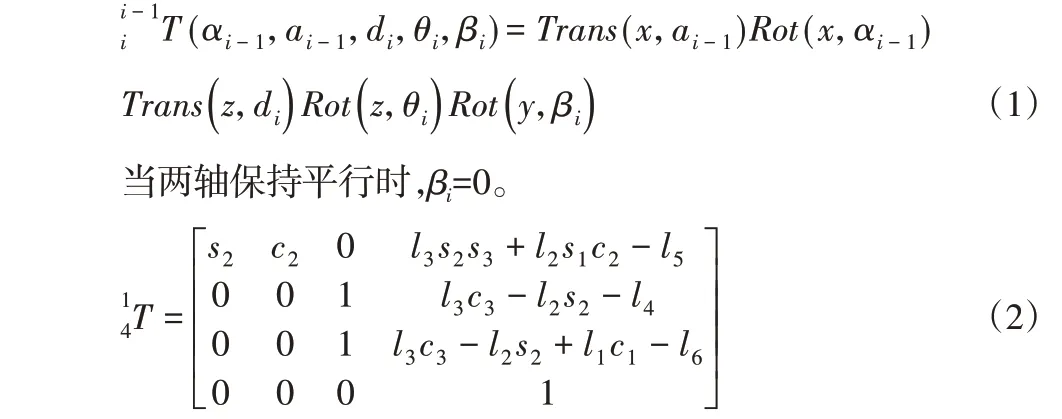
由此可得到机器人足端f相对于坐标轴oo-x0y0z0的坐标向量［fx fy fz］T为：

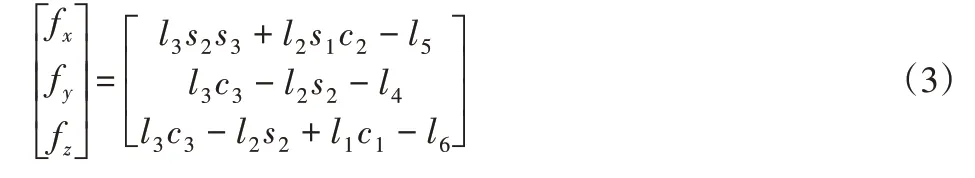
机器人左腿MDH的参数表，如表1所示。

表1 左腿MDH的参数表Tab.1 Parameter Table of Left Leg MDH

由表1可知，可得出机器人各连杆的坐标系之间的关系，根据机器人运动学坐标系的建立方式，可依次确定第i根连杆的齐次坐标变换矩阵Ti-1。下列字母l1－大腿长度、l2－膝骨长度、l3－小腿长度，l5、l6表示距离机器人质心的距离，s1=sinθ1，c1=cosθ2。

祖父家乡观念重。那时广东在外谋生的人不少，喜欢聚集而居，互相往来以广东人自豪。祖父八个儿子找的全是广东媳妇。二伯父病重，祖父从广东找来一个女孩给他结婚冲喜，未等圆房二伯父就死了。祖父很伤心，准备将这个儿媳当女儿嫁出去，但她坚决不离开我们家，于是祖父在广东老家为我的这位二伯母立了贞节牌坊，并给她抱养了个儿子。儿子长大，祖父送他去国外留学，岂料染上肺病，回国不久就病故了。二伯母悲叹自己命太硬，把保姆当作养女，一直在庐山居住，活到97岁，故后葬在庐山。

4.2 四足爬虫机器人腿部步态规划

为了近似描述四足机器人的运动轨迹，满足机器人运动平稳，能适应崎岖道路行走且保持足尖与地面接触时速度和加速度为零的特点，可采用一种修正后的复合摆线的轨迹方程，其足尖在x方向的轨迹方程为：

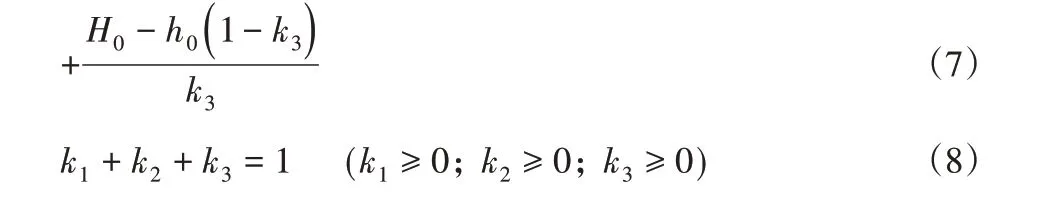
式中：S0－单位摆动前进位移；Ty－单位运动周期；H0－摆动最高

高度；h0－落地点高度；k－时间系数。

腿部运动时，在y轴方向没有位移，x、z轴的轨迹曲线，如式（4）～式（8）所示。

四足机器人的仿真步态运动，如图7所示。按如下方式进行，其步骤如下：

图7 机器人的仿真步态运动图Fig.7 Simulated Gait Motion Diagram of Robot

（1）当机器人的Leg4、Leg1、Leg2 为支撑相时，Leg3 为摆动相，机身旋转一定角度，机身向前运动距离S1，消耗时间为0.2T。

（2）当机器人的Leg1、Leg2、Leg3 为支撑相时，Leg4 为摆动相，机身旋转一定角度，机身向前运动距离S2，消耗时间为0.2T；

（3）当机器人的Leg2、Leg3、Leg4 为支撑相时，Leg1 为摆动相，机身旋转一定角度，机身向前运动距离S3，消耗时间为0.2T；

（5）当机器人的Leg1、Leg2、Leg3、Leg4支撑相时，机身旋转一定角度，机身向前运动距离S5，消耗时间为0.2T。

4.3 梯度投影算法的逆运动学求解

通过上述的动力学的正运动的求解可得出机器人足端的运动坐标，而机器人的逆运动求解是从笛卡尔坐标到关节空间坐标的求解，而机器人的逆运动求解分为封闭解法和数值解法，这里采用基于梯度投影算法的方式求解[fx fy fz]T动力学逆运动的解域，通过给定的足端坐标值来进行对其关节变量的求解，避免产生运动冗余的问题，使得其逆运动有多个运动解，通过雅克比矩阵的逆矩阵反求出其关节变量。

假设其足尖在的坐标矢量为f，关节变量用q表示，根据梯度投影算法可得：

5 运动学仿真

5.1 腿的正运动学与工作空间

机器人的运动轨迹为足端相对于机器人基节坐标系oox0y0z0的工作空间，为了求出机器人的腿部工作域，可设其工作的初始条件：θ1=（-15°50°），θ2=（70°120°），θ3=（-60°0°）。根据其初始条件，可通过matlab 计算出其腿部轨迹域的范围，如图8所示。图8（a）、图8（b）所示，可得出机器人在x轴的运动范围为（-150mm，110mm），y轴的运动范围为（-230mm，120mm），x与y的运动轨迹近乎复合摆线，由此可确定机器人与地面接触时x与y轴的运动速度与加速度为零，机器人y与z轴的位移方向轨迹图，如图8（c）所示。其轨迹为斜率为1.2 的直线，z轴的运动范围为（-280mm，100mm）。机器人在空间的合成位移图，如图8（d）所示。其曲线的空间分布与复合摆线相符，表明仿生机器人的运动分解是可行的，其空间运动坐标可进行adams 仿真步态规划。

图8 足尖轨迹图Fig.8 Foot Tip Trajectory

5.2 腿的逆运动学仿真

通过对参数设定，设置H0=87mm，S0=217mm，S1=S2=S3=S4=S5=38mm，Ty=0.5s，对式（4）～式（8）进行逆运动学求解，利用matlab 对其步态轨迹进行仿真，可求出其关节变量的取值范围，并将机器人的步态轨迹作为仿真的输入条件，可输出机器人关节变量的取值范围，仿真的时间为3s，其时间与角位移的关系，如图9 所示，图9 的q1、q2、q3分别表示其关节的角度θ1、θ2、θ3在（0～3）s 的角位移的变化量，关节变量q1、q2、q3与时间的运动轨迹为正弦函数，q1的范围为（-38～9）°，q2的范围为（63～94）°，q3的范围为（-53～24）°。从上述求解的解集可知梯度投影算法消除了机器人冗余运动解的存在，有效的找出机器人逆运动的解域。通过matlab 将机器人运动轨迹模型导入adams 进行步态规划分析，可得出机械腿足端的速度和机器人重心位移与时间的变化曲线。机器人行走速度，如图10 所示。可看出机器人腿部的速度呈现一个个脉冲的形式，时间间隔小，运动速度均匀。机器人重心位移，如图11 所示。可知机器人每秒位移为25mm，3s 内机器人重心向前运动了75mm，且运动具有连续性，表明该运动平稳且步态位移均匀，避免了因速度波动大对机器人有较大的冲击，从而验证了运动控制方程是正确的，结构设计是合理的，仿生机器人的动作分解是可行的。

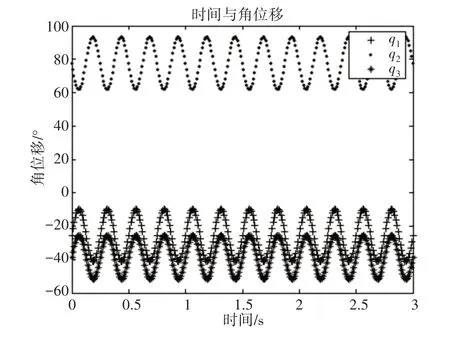
图9 关节变量变化图Fig.9 Joint Variable Change Chart

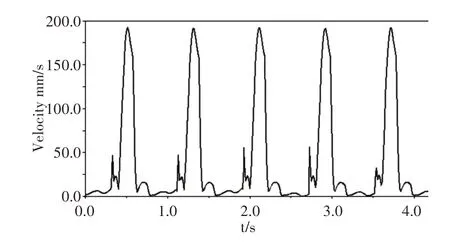
图10 机器人行走速度图Fig.10 Robot Walking Speed Chart

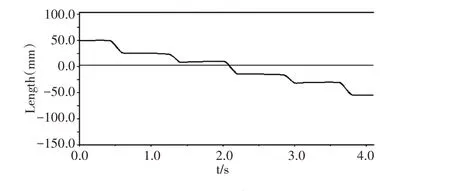
图11 机器人重心位移图Fig.11 Displacement of Robot Center of Gravity

6 结论

（1）仿照蜘蛛结构对机器人的结构进行设计，提出一种修正系数的复合摆线运动轨迹来规划机器人的步态，确保机器人腿部与地面接触无冲击。

（2）通过MDH 法建立机器人的足端的运动轨迹方程，对关节变量q1、q2、q3进行参数化设置，求解出机器人足端的x方向的最大距离为250mm，y轴的最大距离为300mm，z轴方向的极限高度为367mm。

（3）运用梯度投影法对足端轨迹为复合摆线形式的机器人进行关节变量q1、q2、q3的求解，求解出的q1的范围为（-38～9）°，q2的范围为（63～94）°，q3的范围为（-53～-24）°，满足关节变量的初始值范围。

（4）利用matlab将机器人的运动学模型导入adams中进行联合仿真，仿真结果表明机器人腿部的速度呈现一个个脉冲的形式，时间间隔小，运动速度均匀、平稳，运动轨迹与复合摆线方程相符。从而验证了运动控制方程是正确的，结构设计是合理的，仿生机器人的动作分解是可行的。