X80 管道凹痕缺陷失效准则对比分析

伍 颖，田中旭，李林涯

西南石油大学土木工程与测绘学院，四川 成都 610500

引言

石油与天然气是重要的战略资源，被誉为现代工业的“血液”。管道则是石油与天然气最合理的运输方式。截至2017 年底，全球石油与天然气管道总里程已超过233.00×104km[1]，而中国的管道输油（气）里程也在2019 年底达到12.66×104km。然而，随着管道里程的增加，管道事故也呈多发态势。据国家安监总局统计，12.00×104km 的油气管道共排查出29 436 处隐患，平均4.00 km 就有一处[2]。据欧美管道事故统计，美国接近50%的油气管道事故与机械损伤有关，欧洲约70%的油气管道事故是由机械损伤造成[3-4]。机械损伤中最为常见的类型是凹痕，因此，为了保证油气管道的安全运行，就必须对管道凹痕进行安全评价。含凹痕管道的传统评价方法是将凹痕深度达到管道外径的6%作为修复凹痕管道的临界值，然而，疲劳测试证明，采用深度准则并不能准确评估凹痕[5]。由于现有的油气管道大多数为钢制管道，因此，将金属材料的韧性失效准则应用到凹痕管道的评价具有一定的可行性[6]。

传统韧性失效准则考虑的宏观力学影响因子多为第一主应力、等效应力及静水应力等[7]。Cockcroft 和Latham 假定韧性断裂的发生仅与最大主应力相关并提出了Cockcroft-Latham 准则，Oh 等[8]在此基础上提出了修正的Cockcroft-Latham 准则。Oyane 等[9]考虑到静水压力可以抑制或者加速韧性破坏以及应力三轴度的影响，从而提出了Oyane 韧性断裂准则。Allouti 等[10]首次将韧性断裂准则应用到凹痕管道的损伤评估中，并基于Oyane 准则结合数值模拟的方法来分析凹痕深度对管道断裂压力的影响，得到的结果与实验结果具有很好的一致性。伍颖等[11-12]采用Oyane 韧性断裂准则对含单纯凹痕的管道损伤进行了分析。黄超以韧性断裂模型为基础，结合有限元法建立了凹痕管道的损伤模型，计算了平滑凹痕和曲折凹痕不同区域的损伤程度以及不同参数下凹痕缺陷的临界失效应变[13]。党思宏通过研究发现，临界空穴扩张比判据理论可以较好地对凹痕管道的损伤程度进行评价[14]。

近年来，Lode 角被引入了韧性失效准则的研究中[6]。Xue 等[15-17]结合韧性损伤模型与经典可塑性理论提出了X-W 损伤失效准则。Alashti 等[18]通过在有限元分析中引入W 准则、改进的J-C 准则和X-W 损伤失效准则，从而得到在内压作用下凹痕铝管的承载能力。结果显示，X-W 准则是三者之中相对最可靠的。Bai 等[19]通过修正Mohr-Coulomb准则提出了MMC 准则。Hu 等[20]考虑拉伸断裂和剪切断裂两种机制，并假设空洞的长大和连接受两种机制的共同影响，提出了DFC 韧性断裂准则。

随着管道凹痕研究的发展，一些金属材料失效准则被逐步引入到管道凹痕的研究中。但由于缺乏横向对比，难以确定各准则在凹痕管道评价过程中的适用性。因此，本文基于前人对凹痕管道失效准则的研究，选取临界空穴扩张比判据理论、X-W 损伤失效准则和Oyane 韧性断裂准则3 种失效准则，通过有限元模拟，对3 种失效准则评价凹痕管道的结果进行对比分析。为凹痕管道失效准则的研究提供参考，并为凹痕管道评价准则的选取提供依据。

1 韧性失效准则

1.1 临界空穴扩张比判据

郑长卿[21]通过理论推导以及实验研究，提出了宏观形式的临界空穴扩张比参数。宏观形式的临界空穴扩张比在细观形式上对应于空穴扩张比R/R0的临界状态值Rc/R0。临界状态对应于空穴开始聚合（第一代空穴直接聚合或通过第二代空穴聚合）或临聚合状态，这在宏观上对应于材料微裂纹的形成，相当于拉伸试样的应变达到失稳应变。考虑到失稳应变与断裂应变的差别一般在10% 左右，在工程上，定义宏观形式的临界空穴扩张比参数为[21]

对于空穴型损伤的评价，直接采用细观形式的空穴扩张比R/R0，既直观灵敏，又测定方便。但从工程应用的角度讲，R/R0不易直接测得，且对测试的构件具有破坏性。因此，必须将其表达成易于计算、测定及应用的形式。由于R/R0受控于宏观形式的空穴扩张比参数VG，因而可用VG来反映损伤程度。这在力学上是与以细观空穴扩张比反映损伤程度等价的。因此，可用VG来临界空穴扩张比损伤量IV[21]

IV实质上对应空穴发展过程，当IV=1 时，空穴聚合，材料破坏。若已知材料在荷载历史中某个时刻的参数（等效应变ε、静水压力σm及等效应力），结合式（2）可以求得此时材料的韧性损伤程度。其中，X80 材料的临界空穴扩张比参数VGC=2.41[21]。

1.2 X-W 损伤失效准则

X-W 损伤失效准则是韧性损伤模型与经典可塑性理论的结合。在该准则中，软化效应被假定为材料劣化参数，由弱化因子定义。X-W 损伤失效准则具有压力敏感性和Lode 角度依赖性，属于CDM 理论范畴[22-23]。在X-W 损伤失效准则模型中考虑了以下形式的破坏规则的幂函数[11]

压力灵敏度和断裂应变的Lode 角分别由压力隶属函数μ(p)和Lode 角隶属函数μ(θ)决定。压力敏感性和断裂应变的Lode 角隶属函数彼此独立，由压力灵敏度和Lode 依赖函数的乘积得到断裂应变[22]

1.3 Oyane 韧性断裂准则

Oyane 韧性断裂准则假定韧性损伤达到一定值时断裂发生[9]。

材料常数C1、C2至少需要两种应变条件下的断裂应变才能确定。为了得到材料在发生韧性断裂前某一个荷载时刻的积分值，可把式（5）等号两边同时除以常数C2，然后，以等效应变替换等式中的断裂应变εf，将式（5）改写为

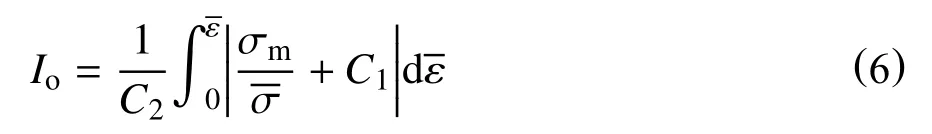
Io体现整个应力-应变历史对材料的韧性损伤程度，且当Io=1 时材料就发生韧性断裂。若已知材料在荷载历史中某个时刻的参数，结合式（6）可以求得此时材料的韧性损伤程度，即Io。

2 Oyane 准则材料常数

为了得到X80 材料的Oyane 韧性失效准则的材料常数，同时为有限元建模提供材料参数，对X80金属材料进行拉伸实验。根据材料力学特性[24]，设计拉单向拉伸实验和平面拉伸实验。试件尺寸如图1所示，实验试件厚度设计为2 mm。

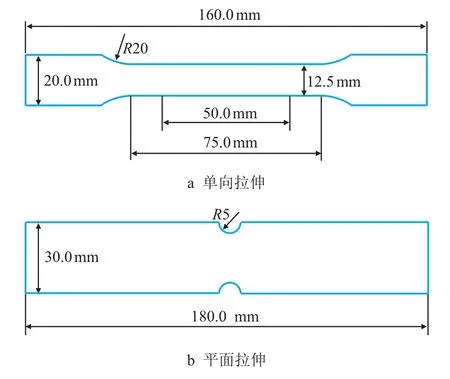
图1 X80 管线钢试件尺寸设计图Fig.1 Dimension design of X80 pipeline steel specimen

在室温下，利用万能实验机对所有待拉伸材料进行拉伸实验，单向拉伸和平面拉伸采用各自的试件尺寸各进行10 次拉伸以减小误差。试件拉伸断裂后形状如图2 所示。对比试样可以发现，变形主要集中在试样中间区域，且试样的断裂位置一致。实验取真实应力最大时刻的应变为试样断裂时的应变，拉伸结果如表1 所示。

图2 试件拉伸断裂图Fig.2 Tensile fracture of specimen

表1 X80 管线钢拉伸实验结果Tab.1 Tensile test results of X80 pipeline steel

根据Hill 屈服准则，在不考虑材料各项异性的情况下，应力三轴度及等效应变与单向拉伸第一主应变的比可简化为式（7），式（8）[24]。

（1）单向拉伸

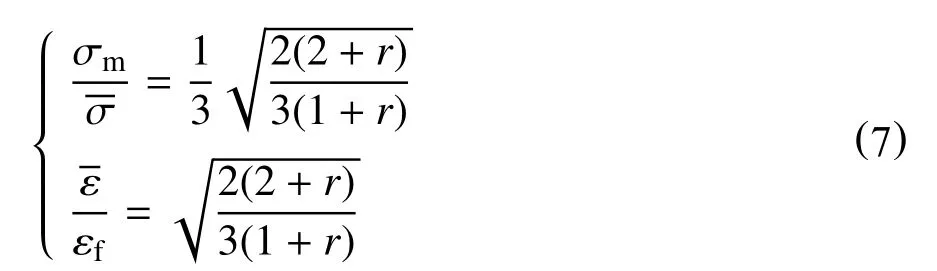
（2）平面拉伸

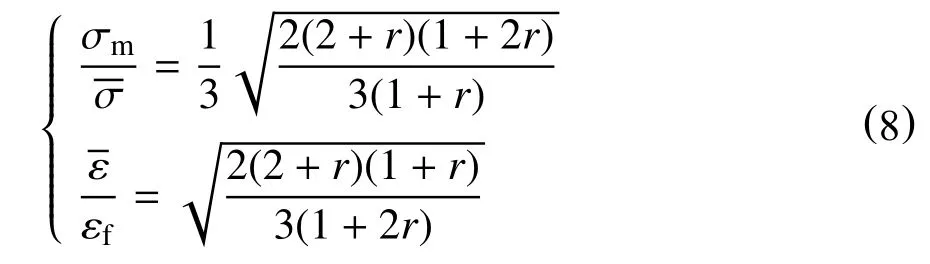
其中，塑性应变比r=1.54[24]。结合式（6）～式（8）及表1 的断裂应变，可求得Oyane 韧性断裂准则中X80 的材料常数为C1=-0.139、C2=0.026。

3 有限元模型

根据X80 材料拉伸实验，得到X80 管道材料的力学性能参数如表2 所示。

表2 X80 管材力学性能Tab.2 Mechanical properties of X80 pipe

3.1 模型尺寸

以长输油气管道为例，建立X80 管道三维实体有限元模型。管道直径1 016 mm，壁厚18.4 mm，设计压力10 MPa。为避免管道两端约束对计算结果的影响，对管长为4～8 倍管径的模型进行试算，结果表明，管道长为6 倍管径不仅能保证在凹痕深度较大时计算数据的准确性，还可以减少有限元计算时间，故将管道长度设为6 倍管径。由于管道模型和荷载条件具有对称性，故以1/4 管道作为分析模型。

3.2 边界条件

管道凹痕有限元模型如图3 所示，分别在管道的对称平面施加对称约束（截面1、2、3），并在管道远离施痕物的截面施加固定约束（截面4）。

图3 管道凹痕有限元模型Fig.3 Finite element model of pipeline dent

考虑到大部分运行中的管道都属埋地式，对管道模型底端约束其y 向自由度，沿管环向的约束范围为120°[25]，如图4 所示。根据凹痕的实际形成情况，将管道施痕物设为刚体。

图4 管底约束Fig.4 Pipeline bottom restraint

3.3 网格划分

由于管道为实体单元，网格选用八节点线性六面体减缩积分单元（C3D8R）。C3D8R 网格单元体对大变形分析非常适用，且计算结果比较精确。为提升计算效率，对管道凹痕区域网格进行局部加密。试算发现，对轴向300 mm、环向60°的管道区域进行局部加密，既能提升计算效率，也能保证有限元计算精度。该模型共有18 360 个网格，网格划分如图5 所示。

图5 管道网格划分Fig.5 Pipeline meshing

3.4 模型验证

为验证有限元模型的准确性，采用上述建模方法，建立管道直径506 mm，壁厚10 mm，管长为1 518 mm 的模型。对管道分别施加5～50 mm 的凹痕缺陷。将有限元计算结果与X80 管道凹痕的足尺实验结果进行对比分析[26]，结果如图6 所示，可以看出，两者的变化规律一致，且各个点的误差均小于10%，因此，建立的有限元模型计算结果符合工程要求。

图6 有限元模型对比验证Fig.6 Comparison and verification of finite element models

4 结果与讨论

4.1 施痕物类型

为研究施痕物形状的影响，根据常见的凹痕类型，采用上述建模方法建立4 种施痕物模型。分别是轴向施痕物、横向施痕物、球形施痕物和矩形施痕物，如图7 所示。除矩形施痕物产生曲折凹痕外，其余3 种施痕物均产生平滑凹痕。其中，椭球形施痕物长轴半径为200 mm，短轴半径为30 mm；球形施痕物半径为100 mm；矩形施痕物为正六面体，边长为200 mm。

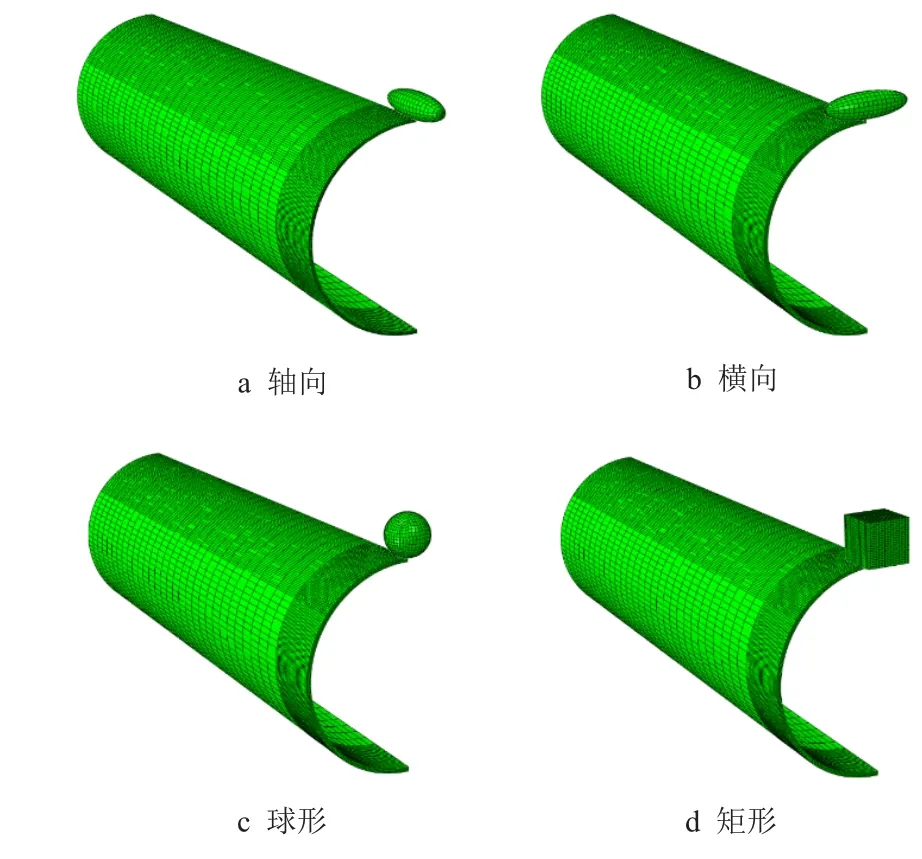
图7 不同凹痕物类型Fig.7 Different types of dent

假设管道尺寸和内压不变，通过改变凹痕类型，计算分析含不同深度凹痕缺陷的X80 管道在3 种韧性失效模型下的损伤量。凹痕深度从0 开始取值，每次增加管道外径的1%。3 种模型损伤量计算结果如图8 所示。

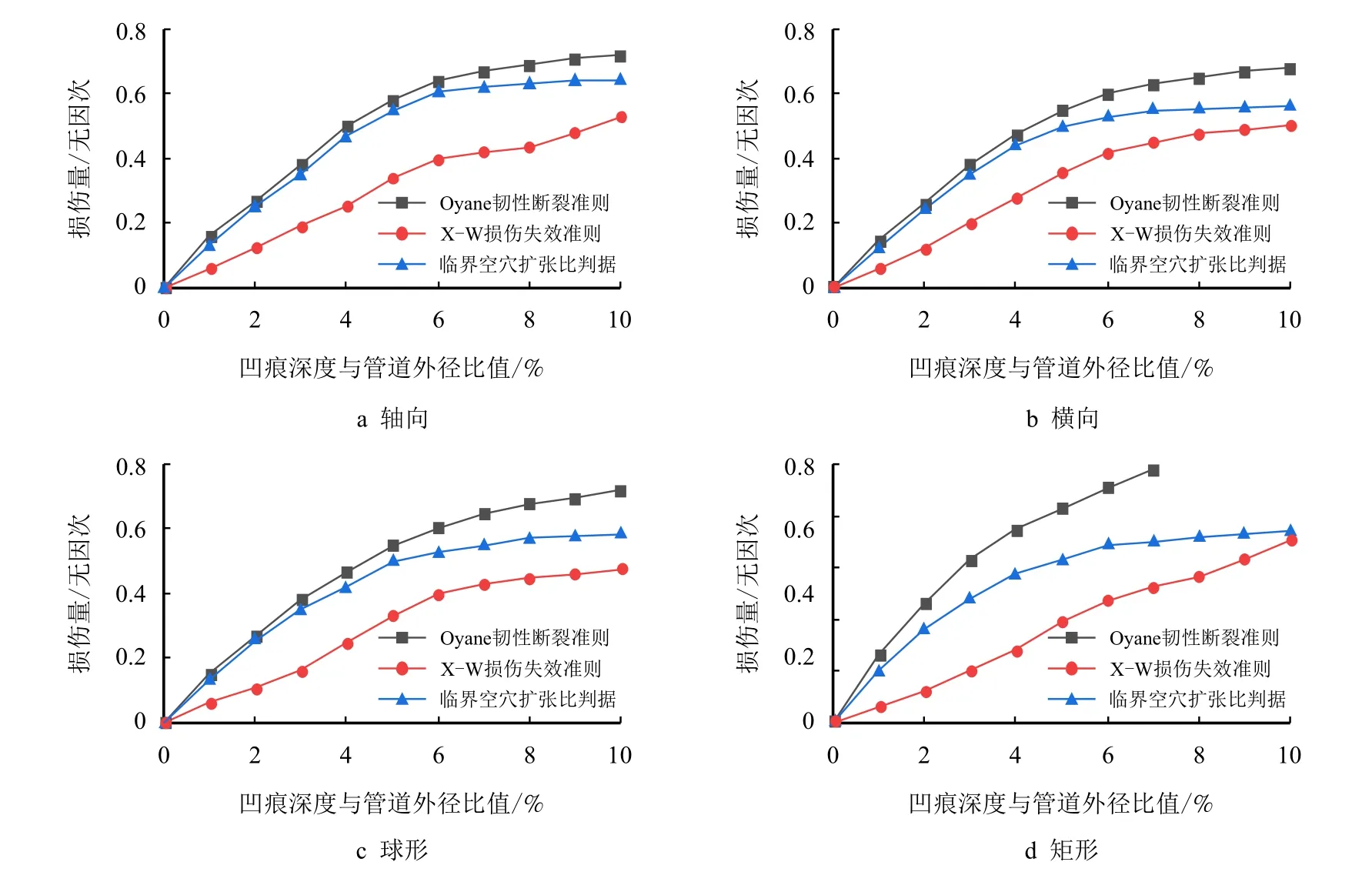
图8 不同凹痕类型下管道损伤量变化曲线Fig.8 Curve of pipeline damage change under different types of dent

由图8 可以看出，3 个韧性失效模型的损伤量均随凹痕深度增加而增大。当凹痕深度小于管道外径的6%时，损伤量随凹痕深度增长较快；当凹痕深度大于管道外径的6%时，损伤量增速放缓。在相同工况下，Oyane 韧性断裂准则的损伤量最大，临界空穴扩张比判据次之，X-W 损伤失效准则最小。

当凹痕类型为平滑凹痕时，Oyane 韧性断裂准则和临界空穴扩张比判据在凹痕深度较小时的评价结果相差不大。当凹痕类型为曲折凹痕时，Oyane韧性断裂准则的损伤量很快便达到其临界值，即Io=1 管道发生韧性断裂；而临界空穴扩张比判据和X-W 损伤失效准则损伤量的增长趋势与平滑凹痕基本一致。由于曲折凹痕更容易在产生凹痕的过程中造成应力集中，对管道的损伤更大，因此，Oyane韧性断裂准则更适合用于曲折凹痕的评价中。

4.2 内压

假设管道的凹痕尺寸以及管道尺寸不变，通过改变管道内压，计算分析含不同深度凹痕缺陷的X80 管道在3 种损伤模型下的损伤量。采用本文的有限元建模方法建立横向施痕物作用下的管道模型。分别取管道内压为6、8、10 及12 MPa，凹痕深度从0 开始取值，每次增加管道外径的1%，极限凹痕深度为10%。

依据有限元计算结果，分别采用3 种失效准则计算不同内压下管道凹痕的损伤量，损伤量变化曲线如图9 所示。

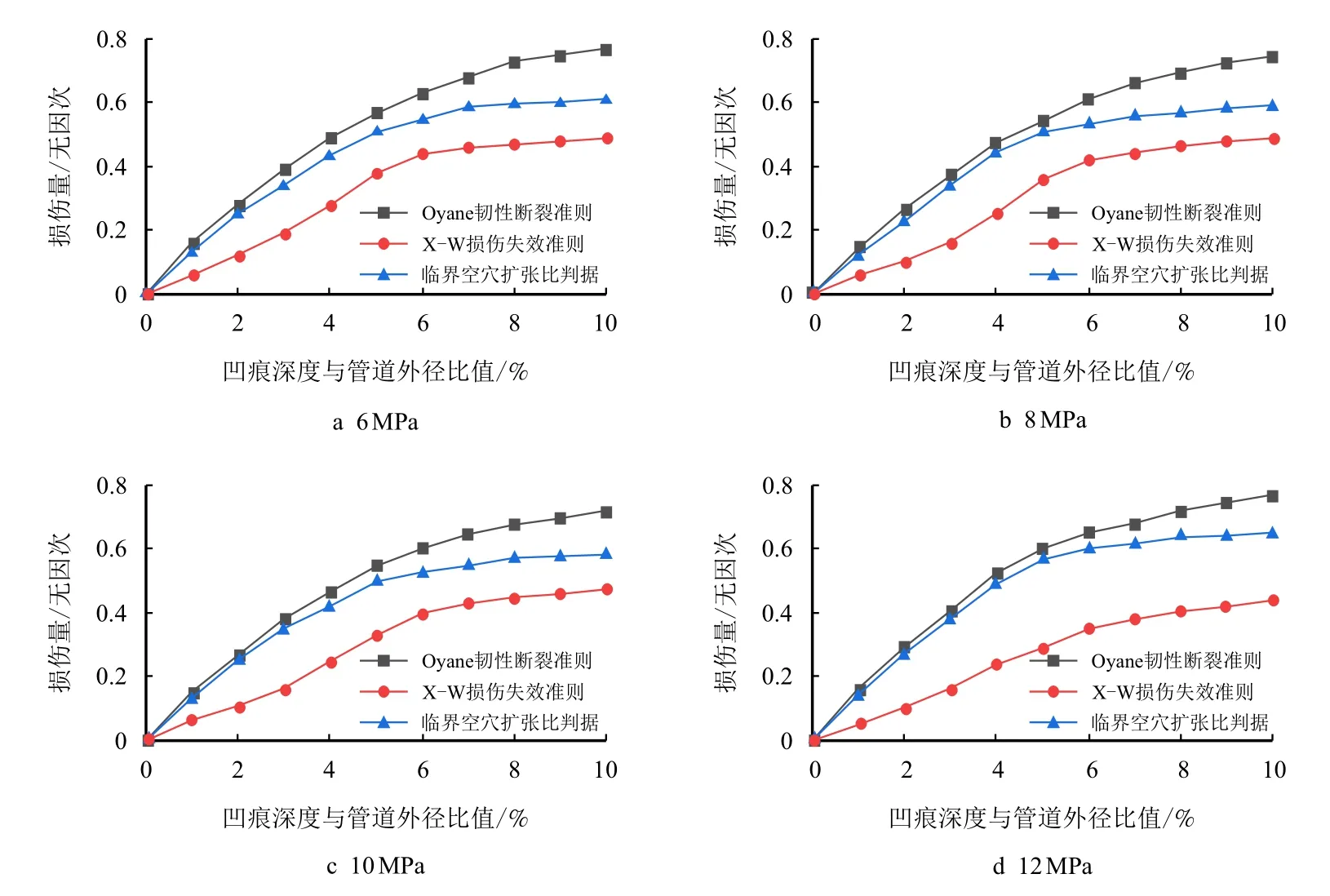
图9 不同内压下管道损伤量变化曲线Fig.9 Curve of pipeline damage change under different internal pressure

由图9 可以看出，不同内压下3 个韧性失效模型损伤量的变化规律与4.1 类似。损伤量随凹痕深度增加而增大。当凹痕深度小于管道外径的6%时，损伤量随凹痕深度增长较快；当凹痕深度大于管道外径的6%时，损伤量的增速放缓。在相同工况下，Oyane 韧性断裂准则的损伤量最大，临界空穴扩张比判据次之，X-W 损伤失效准则最小。

当凹痕深度超过管道外径的6%后，临界空穴扩张比判据准则和X-W 损伤失效准则的损伤量增长幅度较小。当管道内压为6 MPa，凹痕深度从管道外径的7%增大至管道外径的10%时，临界空穴扩张比判据计算的损伤量增长率为5.6%，X-W 损伤失效准则计算的损伤量增长率为4.1%，而Oyane 韧性断裂准则计算的损伤量增长率为13.2%。这就表明，在不同管道内压条件下，Oyane 韧性断裂准则对管道凹痕的评价结果是3 个损伤模型中最保守的。

4.3 径厚比

假设管道的凹痕尺寸以及管道运行内压不变，通过改变管道径厚比，计算分析含不同深度凹痕缺陷的X80 管道在3 种损伤模型下的损伤量。采用本文的有限元建模方法建立横向施痕物作用下的管道模型。运行内压为10 MPa。依据管道设计参数，当壁厚为18.4 mm 时，管道径厚比D/t=55，故径厚比分别取35、45、55 及65。凹痕深度从0 开始取值，每次增加管道外径的1%，极限凹痕深度为管径的10%。3 种失效准则计算结果如图10 所示。

图10 不同径厚比下管道损伤量变化曲线Fig.10 Curve of pipeline damage change under different diameter thickness ratio

由图10 可以看出，不同径厚比下3 个韧性失效模型损伤量的变化规律与内压相似。当凹痕深度相同时，X-W 损伤失效准则的损伤量和其他两者相差较大，而当凹痕深度较小时，Oyane 韧性断裂准则和临界空穴扩张比判据计算的损伤量相差不大。纵向对比，当凹痕深度小于管道外径的6%时，Oyane韧性损伤断裂准则和临界空穴扩张比判据计算的损伤量很接近，而X-W 损伤失效准则的损伤量偏小；当凹痕深度大于管道外径的6%时，临界空穴扩张比判据和X-W 损伤失效准则的损伤量增长率趋于平缓，约1.0%左右；而Oyane 韧性断裂准则的损伤量增长率大于3.0%。由此可以看出，Oyane 韧性断裂准则更适合用于深度较大的管道凹痕评价中。

5 结论

（1）Oyane 韧性断裂准则、X-W 损伤失效准则和临界空穴扩张比判据所计算损伤量在表示含凹痕缺陷的管道损伤程度时都具有较强的规律性，且损伤量随着损伤程度的增大而单调递增，故3 个失效准则计算的都可以用于表示管道凹痕的损伤程度。

（2）X-W 损伤失效准则和临界空穴扩张比判据在凹痕深度大于管道外径的6%之后，其损伤量随管道凹痕深度的增长幅度相比Oyane 韧性断裂准则小，这说明Oyane 韧性断裂准则更适合用于深度较大的管道凹痕评价中。

（3）在相同工况下，Oyane 韧性断裂准则的损伤量最大，临界空穴扩张比判据次之，X-W 损伤失效准则最小。且在本研究中，只有Oyane 韧性断裂准则的损伤量达到过韧性断裂的临界值，其余两种失效模型在不同工况下计算的损伤量距断裂临界值还有一定差距。这表明，Oyane 韧性断裂准则在评价凹痕管道中相对更为保守。

（4）在曲折凹痕的评价中，Oyane 韧性断裂准则计算的损伤量能更快地达到断裂的临界值。相比其余两种模型，Oyane 韧性断裂准则能更好地反映曲折凹痕的应力集中，更适合用于管道曲折凹痕的损伤评价。

符号说明

R空穴扩张到某瞬时的折算半径，mm；

R0空穴形核时的折算半径，mm；

Rc空穴扩张到临界状态的折算半径，mm；

VGC临界空穴扩张比参数，无因次；

εf断裂应变，无因次；

Rσ应力三轴度状态参数，无因次；

IV临界空穴扩张比损伤量，无因次；

VG空穴扩张比参数，无因次；

σm静水压力，MPa；

IXWX-W 损伤失效准则损伤量，无因次；

εeq等效应变，无因次；

mX-W 损伤失效准则常数，无因次；

εf0X-W 损伤失效准则参考等效断裂应变，无因次；

μ(p)压力隶属函数；

C1，C2Oyane 韧性断裂准则材料常数，无因次；

IoOyane 韧性断裂准则材料损伤量，无因次。