内压作用下含凹痕管道三维应变计算新方法
伍 颖 吴 鹏 张 媛 鄢小兵
1. 西南石油大学土木工程与测绘学院 2. 东方电气集团东方锅炉股份有限公司 3.中国石油西南油气田公司川中油气矿
0 引言
油气管道在搬运和回填的过程中经常会发生管道碰撞或岩石等外物压砸管道的情况,造成管道凹痕缺陷[1-8]。凹痕是指由于管壁永久塑性变形而使管道横截面发生的总的变形,是造成长输油气管道失效的一个常见原因[9-10]。凹痕缺陷会改变管体局部应力、应变状态[11],并增加管道的失效敏感性,直接影响管道的局部应变、剩余强度和疲劳寿命[12]。因此,需要对油气管道上的凹痕进行正确评估,以判断是否对变形管段进行修复或更换[13-14]。
传统的基于凹痕深度的评价标准,忽略了凹痕其他的几何形状特征,忽视了凹痕区域的局部应变和应力分布,会导致管道的安全状况被高估或低估[15]。因此,Rosenfeld等[16]提出了基于应变的评价思想,美国机械工程师协会ASME B31.8-2003[17]将该思想纳入其中,制订了从应变的角度评估凹痕缺陷的准则,成为传统深度准则的替代方案。为了获得凹痕区域应变,ASME B31.8-2003[17]中给出了计算凹痕区域等效塑性应变的非强制表达式,随后在ASME B31.8-2007[18]、ASME B31.8-2018[19]中进行了部分改进。Baker等[20]认为标准中没有指明应变计算的假设条件和应变确定的依据,计算等效塑性应变的方法需要进一步改善。Lukasiewicz等[21]综合采用数学方法和基于壳单元的有限元模型,针对管道特有的圆形薄壳结构进行了凹痕应变求解,但由于该模型考虑了管材的非线性本构关系,在涉及大变形问题时计算十分复杂。Tindall等[22]利用漏磁检测数据来预测凹痕的轴向弯曲应变[23],提出了将轴向弯曲应变作为衡量凹痕严重程度指标的预测模型,不过该模型只考虑了凹痕处的轴向弯曲应变,因此存在一定的局限性。冯庆善等[24]利用惯性测绘数据,提出了基于弯曲应变的管道凹痕建模计算方法,但该方法也只考虑了弯曲应变与凹痕深度的关系。Adrian等[25]利用管壁质点在发生变形时产生的位移进行应变求解,但作者假设管道发生凹痕变形时只存在径向位移,这就使得计算结果缺乏可信度。Husain[26]使用概率统计方法推导了管道凹痕区域应力应变的数学解析式,但该方法公式过于复杂,不利于工程实际应用。笔者团队也从凹痕轮廓插值和应变计算方面对凹痕评价进行了研究,通过弯曲应变使用关系表达式计算膜应变可以得到很好的结果,但是这只针对特定情况,不具有普遍性[27-28]。上述应变计算方法在一定程度上能够得到误差更小的凹痕区域的应变结果,但是存在假设条件过多、局限性高、计算复杂、不利于工程实际应用的问题。Chike等[29-32]针对无压管道形成的约束凹痕,通过以位移函数来定义凹痕轮廓,提出了基于应变张量进行应变求解的方法,但针对有压管道及非约束凹痕的适用性还有待进一步研究。综上所述,目前国际上仍尚无精确的分析方法用于确定实际管道凹痕处的应变[33],并且过去的研究都忽略了剪切应变的计算,导致凹痕处总应变的确定可能存在偏差。
笔者提出了一种考虑剪切应变的计算内压作用下含约束型和非约束型凹痕管道应变的新方法。首先,采用有限元方法对管道上约束凹痕和非约束凹痕的产生过程进行了数值模拟,分析了管道内外壁等效塑性应变沿管道轴向、环向的分布规律,然后通过对凹痕变形区域进行三维插值生成定义凹痕表面的位移函数,最终采用以应变张量形式分析凹痕区域应变的解析模型,建立了考虑剪切应变的管道凹痕区域应变计算模型。考虑剪切应变的计算模型能够更为准确地反应管道凹痕区域的应变分布,能为评估凹痕缺陷的严重程度提供一定的参考。
1 有限元数值模型
1.1 管材参数
管材选用API 5L X80管线钢,管材的特性参数如表1所示[34]。

表1 钢管的材料性能表
1.2 有限元模型建立
采用ABAQUS软件建立椭球形压头作用于管道的三维实体模型,椭球形压头如图1所示。笔者重点在于提出一种考虑剪切应变的计算内压作用下含约束型和非约束型凹痕管道应变的新解析方法,而不是研究凹痕尺寸对应变的影响规律,因此假设椭球形压头短轴a、c大小相等,长轴为b。压头模型采用离散刚体建立,管道采取八节点线性六面体实体单元C3D8R建立,采用各向同性硬化模型。以国际上常用的准静态分析方法模拟凹痕的形成,准静态模拟以分步或多步将载荷非常缓慢地加载到管道结构上,相对于动态模拟可以忽略惯性效应[35-36]。由于管道模型和荷载的对称性,建立了1/4对称模型。通过在网格分布中产生一些偏差来优化数值模拟的计算时间,局部网格细化分配在凹痕区域,而粗网格应用于管道模型的其他区域。

图1 椭球形压头图
有限元模型及网格划分情况如图2所示。
图2 有限元模型网格划分图
压头加载采用位移加载方式。对受压工况下的含约束凹痕管道进行模拟时,通过合理简化,主要载荷加载步骤为:①建立接触;②施加位移荷载;③施加内压。对于非约束凹痕,有限元分析中的加载步骤为:①建立接触;②施加位移荷载;③卸载位移;④施加内压。非约束凹痕由于压头的移除会导致凹痕区域的弹性变形恢复,再施加内压会进一步导致凹痕区域的塑性变形得到部分恢复,因此凹痕深度会减小。其中,内压采用均布压力载荷的方式均匀施加在管道的内表面。约束凹痕及非约束凹痕的有限元加载步骤分别如图3、4所示。

图3 约束凹痕加载步骤图
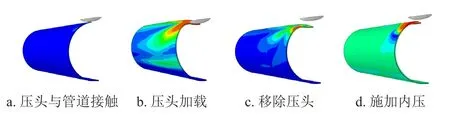
图4 非约束凹痕加载步骤图
1.3 有限元模型验证
为了验证所建有限元模型的可靠性,对Naghipour等[37-38]中的实验进行了数值模拟分析,并将模拟结果与试验值进行对比。试验管材为X80钢,试验管道长度为290 mm,管径为44 mm,壁厚为2 mm,压头为直径20 mm的半球。笔者建立了与试验管参数一致的有限元模型,试验结果和数值模拟结果对比如表2所示。从表2可以看出,该数值模型与试验结果具有较好的一致性。将试验边界条件误差考虑在一定范围内是合理的,因此可以认为所建立的数值模型是有效的。

表2 实验结果和有限元结果比较表
1.4 有限元应变结果分析
1.4.1 非约束凹痕
建立椭球形压头按压管道形成非约束凹痕的有限元模型,压头短轴(a=c)为120 mm,长轴(b)为400 mm,管道外径(D)为1 016 mm,壁厚(t)为15.3 mm,管道长度为3 048 mm,设计压力为10 MPa,管道几何尺寸选自国内某在役长输管道的实际数据。凹痕深度(d)范围为1%D~12%D(即10.16~121.92 mm)。图5、6分别显示了不同凹痕深度下凹痕区域管道内外壁沿管道环向和轴向的等效塑性应变分布情况。
从图5-a可知,沿管道环向,最大等效塑性应变点始终位于凹痕中心的管道内表面,但随着距凹痕中心距离的增加,应变值的变化规律呈现较为频繁的波动。从图5-b可知,管道外壁的等效塑性应变随着距凹痕中心距离的增加不断减小,最大等效塑性应变位置同样位于凹痕中心,但管道外壁的应变远小于管道内壁的应变。
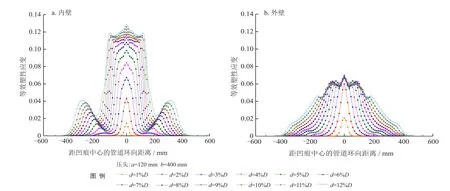
图5 非约束凹痕沿管道环向的等效塑性应变变化图
从图6可知,沿管道轴向,不论管道内表面还是外表面,凹痕区域等效塑性应变值的变化趋势相似,但外壁等效塑性应变小于管道内壁。对比图5、6,由于非约束凹痕失去压头的限制,因此会在内压作用下发生塑性回复,导致凹痕区域边缘的应变发生波动。

图6 非约束凹痕沿管道轴向的等效塑性应变变化图
1.4.2 约束凹痕
建立椭球形压头按压管道形成约束凹痕的有限元模型,有限元模型几何尺寸不变。图7、8分别显示了不同凹痕深度下凹痕区域管道内外壁沿管道环向和轴向的等效塑性应变分布情况。
从图7-a可知,等效塑性应变随着距凹痕中心沿管道环向距离的增加而呈非线性变化,最大等效塑性应变点始终位于凹痕中心。从7-b可知,凹痕区域管道外壁的等效塑性应变随着距凹痕中心的管道环向距离的增加而不断减小直至0,最大等效塑性应变位置同样位于凹痕中心,但管道外壁的应变远小于管道内壁的应变。这可能是因为管道施加内压后,由于受到压头的限制,管道外表面处于受压状态而管道内表面处于受拉状态,因此导致管道内壁的塑性应变急剧增加。
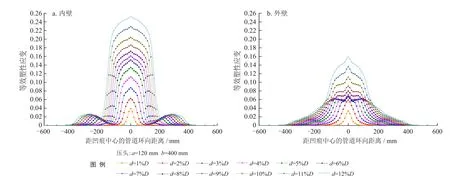
图7 约束凹痕沿管道环向的等效塑性应变变化图
从图8-a可知,凹痕区域管道内壁的等效塑性应变值随轴向距离的增加而不断变化,但与管道环向相比,管道轴向的塑性变形区域更小,在很短的一段距离内等效塑性应变急剧减小。从图8-b可知,凹痕区域管道外壁的等效塑性应变值的变化规律与内壁相似,但由于外表面直接受到压头的限制作用,在内压作用下更容易受到压头的影响而产生塑性变形。此外,对比同等条件下的非约束凹痕,含约束凹痕的管道产生了更大的应变。

图8 约束凹痕沿管道轴向的等效塑性应变变化图
2 解析模型
解析模型参照了Chike等[29-32]提出的基于应变张量进行应变求解的方法,在此基础上建立了考虑剪切应变的管道凹痕区域应变计算模型。
2.1 凹痕轮廓插值
凹痕区域应变可以通过对在线检测工具的数据点插值形成变形轮廓来估计。选择3次B-样条来插值形成凹痕区域连续且可微分的三维拓扑曲面。样条曲线遵循由凹痕坐标定义的控制多边形的形状,并且不围绕任何直线振荡。相邻样条函数的一阶导数在它们相遇的节点处相等,二阶导数也设为零。在这些条件下,由该方程可以得到插值常数,以分段的方式应用在管道的凹痕变形区域,因此可获得凹痕区域连续且可微分的轮廓表面。
以椭球形压头形成的6%D(60.96 mm)约束凹痕为例,通过直接从数值模型的节点提取矢量位置来获得插值点,并将有限元节点坐标转换到圆柱坐标系(R,θ,Z)中。用于内插凹痕表面的数据点对应于在圆周方向上具有64个传感器的在线检测工具的分辨率,并且沿着管道的纵轴以每15 mm的间隔获得数据。从凹痕顶点所在的横截面作为镜像中心,分析了沿管道长度300 mm的变形。使用计算工具MATHEMATICA完成对数据点的插值,示例凹痕内表面的三维插值曲面如图9所示。

图9 6%D约束凹痕插值内表面图
2.2 几何变形分析
2.2.1 基本假设
用于插值凹痕轮廓的样条函数定义了管道内表面的几何变形,因此可以通过分析管道中表面的变形获得管道在轴向、环向和径向的位移。所做的基本假设为:①假设凹痕顶点处经历的变形是纯径向的;②假设变形过程中管壁厚度没有减少;③假设管道在环向上不可延伸。
2.2.2 位移分解
定义凹痕顶点所在的角位置在0 rad处,整个圆周方向的角位置范围为[-π, π]。图10显示了变形管的中面横截面的示意图,变形管道中间表面半径为Rm,R0代表截面未变形的初始中面半径,即为管径(D)与壁厚(t)之差的一半。若一个点从未变形轮廓中的m移动到变形轮廓中的m',管道变形后质点的角度变化为φ,则质点所移动的位移与角变形(φ)和中表面的环向位移有关。
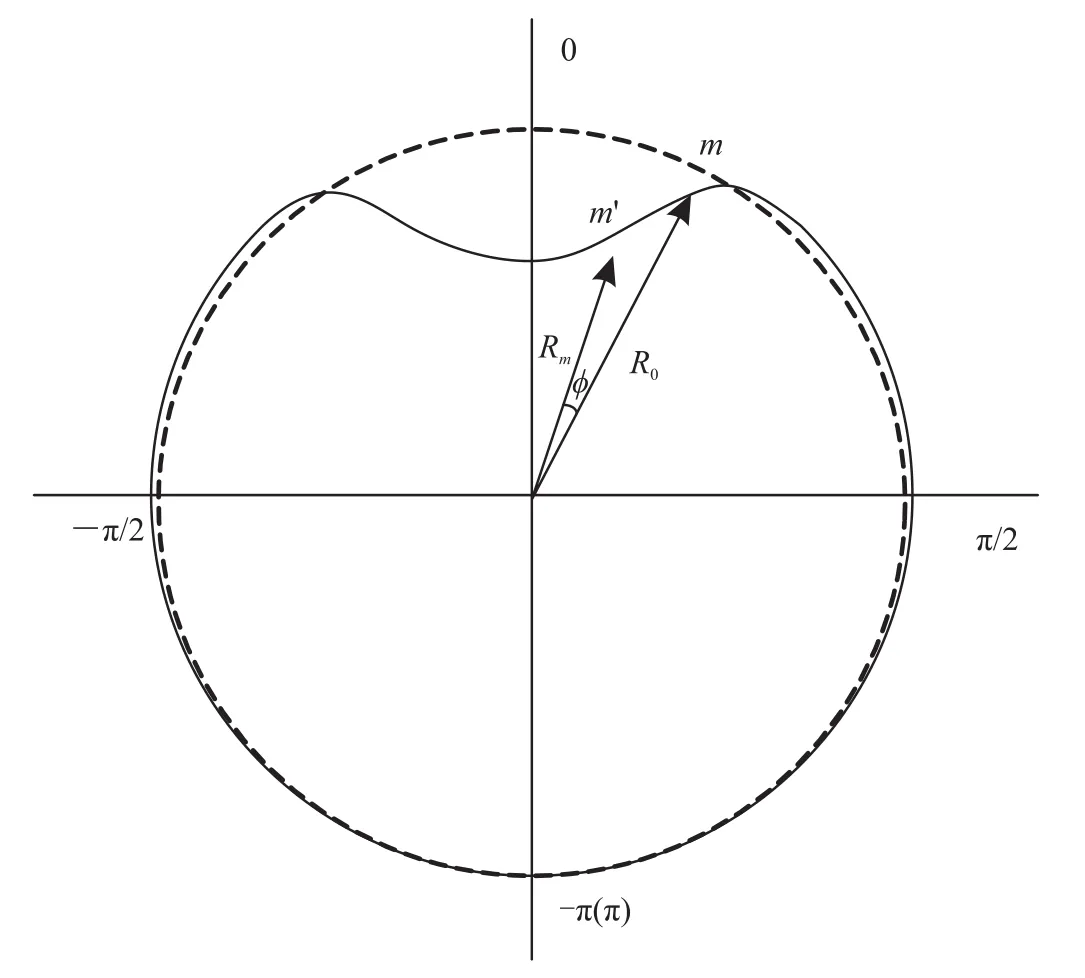
图10 变形和未变形状态下管道中表面的剖面图
通过在线检测得到的数据是变形管道内壁半径(Ri)和每个检测点的相应角度位置(θ)。管壁中间表面的半径(Rm)可以被评估为管道内壁半径和管道厚度方向分量的总和。使用下式评估该半径:

管道中表面径向位移(urm)为:
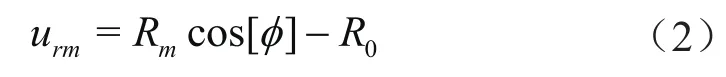
管道中表面的环向位移(uθm)为:

管道的整体环向变形与管壁的椭圆化和由管壁在环向轴线上的倾斜引起的管壁局部变形有关。作为变形的结果,变形后的矢量位置与原始位置之间的环向角度形成三角关系,图11显示了管道在环向(R,θ)平面的变形,其中er和eθ表示为管道在径向和环向方向上的单位矢量,θθ表示变形管道的中间表面在环向方向上形成的偏移角度。

图11 管道在环向(R, θ)平面的变形图
管道内表面的位移是管壁厚度的函数,管内壁环向位移(uθ)为:
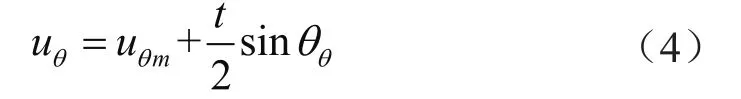
管内壁径向位移(ur)为:
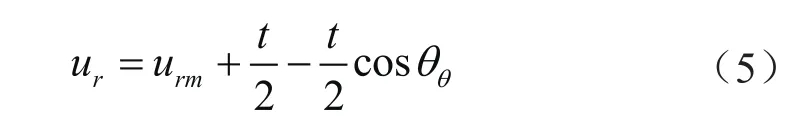
其中θθ的计算方法如下:

变形管道的中间表面在轴向方向上形成偏移角度(θz),在管道的中间表面处,轴向位移(uzm)为0。内表面轴向位移(uz)由下式计算:

其中管壁轴向变形角度(θz)为:

2.3 应变测量
变形轮廓坐标以径向位置(R)、角位置(θ)和轴向位置(Z)表示。管道变形在柱坐标系中管道的全局位移场(u)的定义为:

式中ez表示管道轴向方向上的单位矢量。
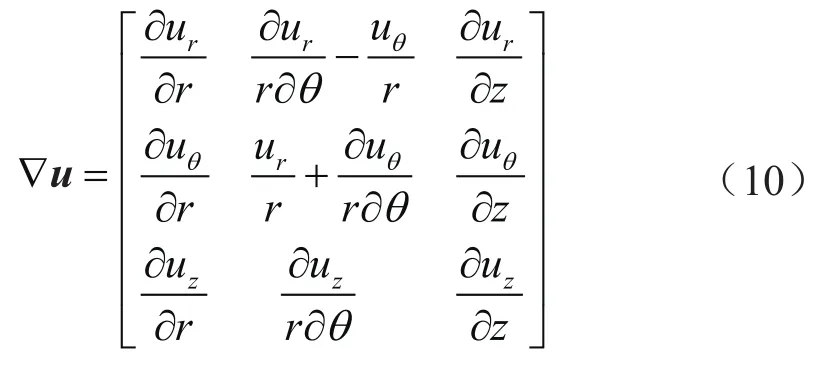
式中r表示管道的可变半径,mm,它是管道的假设中间表面半径(R0)与管壁厚度之和。
根据拉格朗日应变张量的定义,可得到格林—拉格朗日应变张量(E)为:
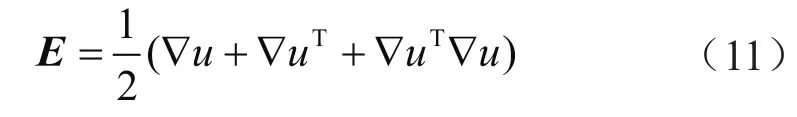
上述应变公式包含非线性项,因而可以解释与变形相关的大变形和旋转。当进行线性应变或小应变测量时,假设变形体材料颗粒的位移无穷小,因此在变形过程中,物体的几何形状不会发生变化。小应变张量(e)的定义表示为:
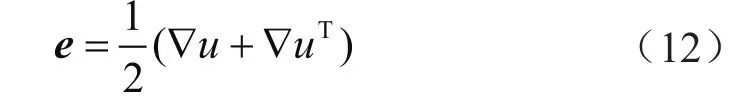
假设所研究的应变方向均在主轴上,则应变矩阵中的对角线应变分量εrr、εθθ和εzz分别代表径向、环向和轴向应变分量;非对角线应变分量εrθ、εθz和εrz分别代表剪切应变分量。
在轴向方向,当管道发生凹痕变形时,以管壁膜的延伸为特征在轴向上发生较大变形,因此采用非线性拉格朗日应变测量,能够获得由于管道的膜延伸引起的应变。轴向应变的数学表示为:

在环向上,由于假设管道在环向上不可延伸,即管道变形后环向的总长度仍然保持不变,因而在该轴上管道发生了小的旋转和小变形,应使用线性小应变公式来评估环向应变,其数学表达式为:
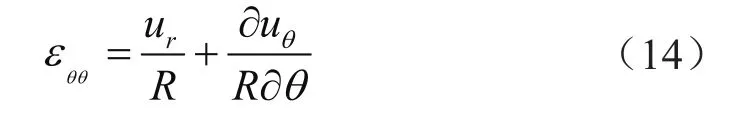
由于凹痕区域发生较大的塑性变形,可以忽略弹性的体积变化,认为材料在塑性状态时的体积不可压缩,这意味着有效应变矩阵的迹的和是0,则径向应变公式为:

将3个方向的应变分量和剪切应变进行分析组合,能够得到管道凹痕段的等效总应变为:
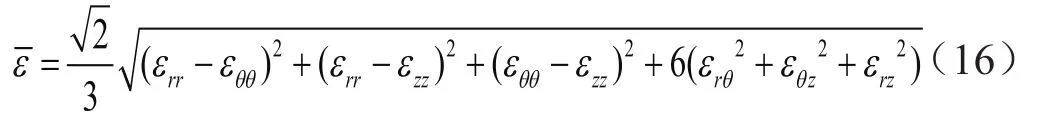
若不考虑剪切应变,用径向、环向、轴向的应变作为主应变表示时,
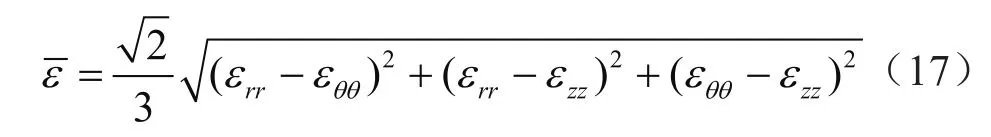
3 结果分析
3.1 非约束凹痕
3.1.1 变形对比分析
以初始加载深度为6%D(60.96 mm)的非约束凹痕为例,通过解析模型求解整个凹痕管道区域的方向位移表达式,这些表达式的解由分析模型得到的等值线表示(图12~14),得到的管内壁径向位移、环向位移、轴向位移分布如图12-a、13-a、14-a所示。数值模拟得到的凹痕管道的径向位移、环向位移、轴向位移分布如图12-b、13-b、14-b所示。
从图12-a可以看出,解析模型预测的变形区域中心的径向位移最大,最大径向位移为25.00 mm,负号代表发生向内的变形。径向位移由初始加载深度6%D(60.96 mm)减小到25.00 mm,这是因为压头移除后,凹痕区域发生回弹现象,导致凹痕深度减小。随着距凹痕中心沿管道轴向、环向距离的增加,径向位移不断减小直至为0,与图12-b中有限元预测的顶点最大径向位移为25.85 mm的结果一致。
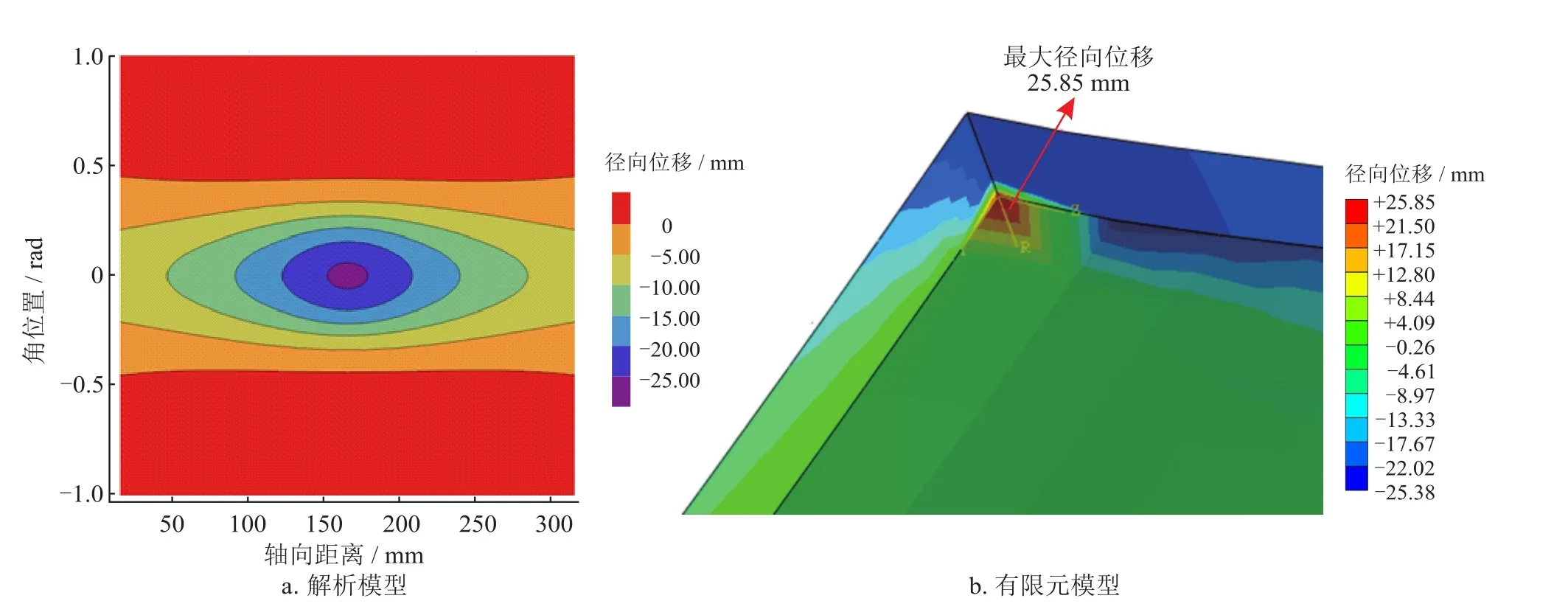
图12 解析模型和有限元模型预测的径向位移图
从图13-a可以看出,沿管道环向方向,凹痕区域肩部出现了明显的椭圆化现象。沿管道环向方向,凹痕顶点另一侧会出现对称的环向位移分布,负号表明为管壁发生反向的延伸。从图13-b可以看出,有限元计算得到的最大环向位移出现在凹痕区域的侧部,且最大环向位移量为25.65 mm,远大于解析模型。这可能是由于解析模型中采用了管道环向不可延长的假设,才导致管道的环向位移被低估。但是在凹痕评估中,影响凹痕缺陷严重程度的主要因素为径向位移,环向位移对凹痕缺陷评估影响不大,所以本模型可以很好地对凹痕缺陷进行评估。
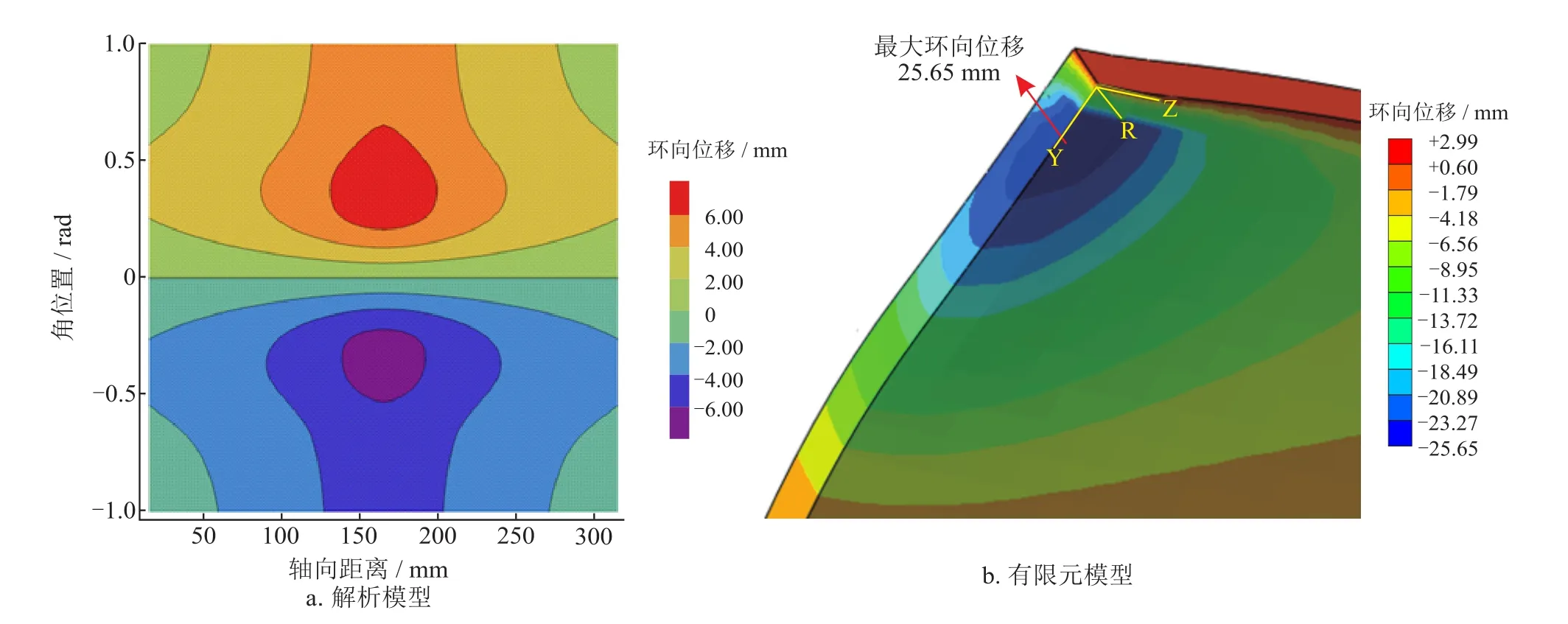
图13 解析模型和有限元模型预测的环向位移图
从图14-a可以看出,解析模型得到的管道最大轴向位移出现在凹痕区域的侧部,最大轴向位移为1.00 mm。变形区域的轴向位移沿凹痕顶点对称分布,正负号代表管壁沿轴向延伸的方向。从图14-b可以看出,数值模拟预测的最大轴向位移同样位于凹痕区域的管道内壁,且最大轴向位移量为1.50 mm,有限元模型与解析模型的预测基本一致。
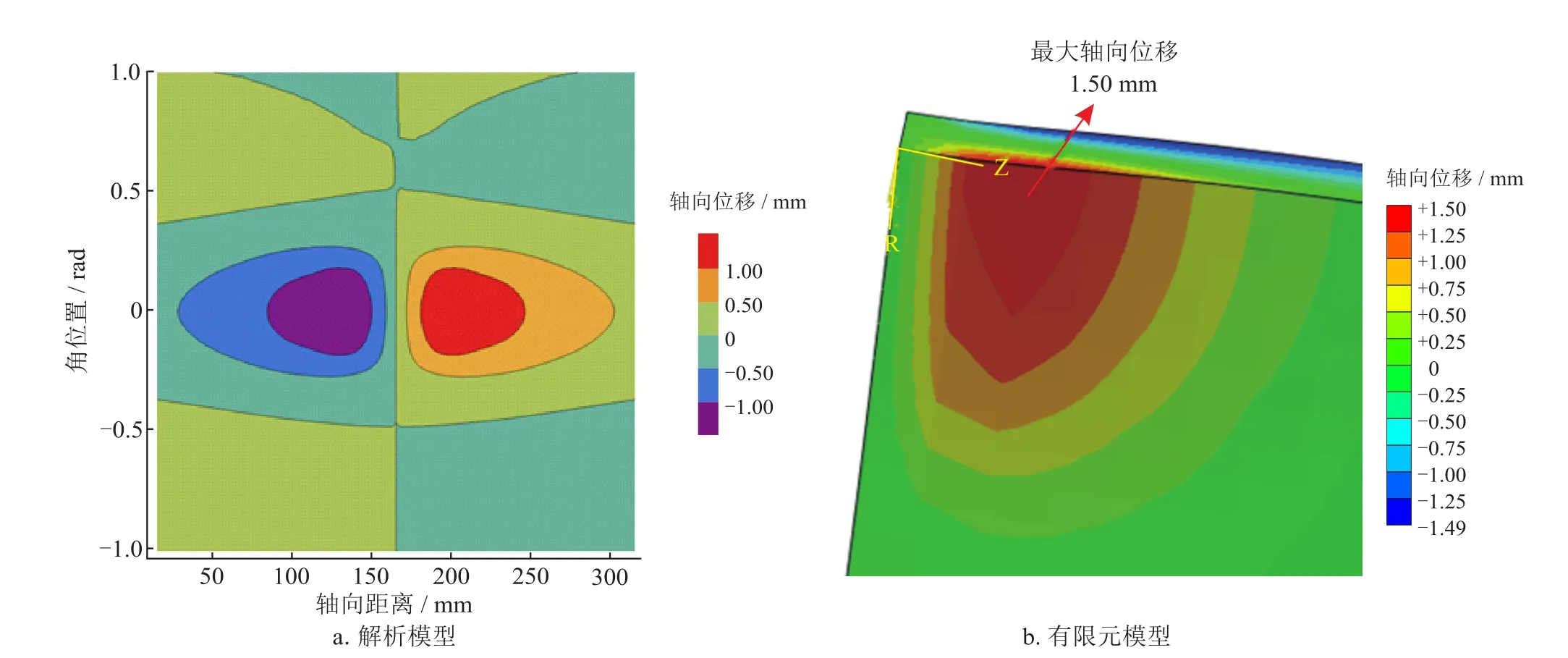
图14 解析模型和有限元模型预测的轴向位移图
3.1.2 应变对比分析
通过解析模型求解管道凹痕区域的应变张量,各分量的值在分析模型得到的等值线图上表示(图15~17)。解析模型预测得到的管道内表面的径向应变分量、环向应变分量、轴向应变分量分别如图15-a、16-a、17-a所示,有限元模拟得到的管道内壁径向应变、环向应变、轴向应变分别如图15-b、16-b、17-b所示。

图15 解析模型和有限元模型中管内壁的径向应变图
从图15-a可以看出,解析模型求得的管道内表面最大径向应变位于凹痕中心,值为0.100,负值代表压缩应变。随着距凹痕中心沿管道轴向、环向距离的增加,径向应变不断减小直至为0。从图15-b可以看出,有限元模拟得到的管道内表面最大径向应变同样位于凹痕中心,值为0.071,与解析模型预测结果存在较小差异。
从图16-a可知,解析模型预测的管内壁最大环向应变的位置位于凹痕中心,值为0.010。图16-b中观察到有限元分析得到的管道内壁最大环向应变点偏于凹痕顶点,位于凹痕顶点所在管道横截面上凹痕区域的侧部,管道内壁最大环向应变为0.069,大于解析模型对内壁环向应变的预测。这可能是由于上述提到的解析模型中对圆管环向不可延长的假设使得管壁环向变形被低估,因此导致了解析模型预测了较小的环向变形而使得估计的环向应变值偏小。

图16 解析模型和有限元模型中管内壁的环向应变图
从图17-a观察到管内壁的凹痕顶点位置的轴向应变最大,值为0.090,沿管道环向和轴向随着距离凹痕中心距离的增大,管道内表面各点的轴向应变呈不断减小的趋势。数值模拟得到的管道内壁最大轴向应变为0.067,同样位于凹痕中心,但值略小于解析模型预测的轴向应变。
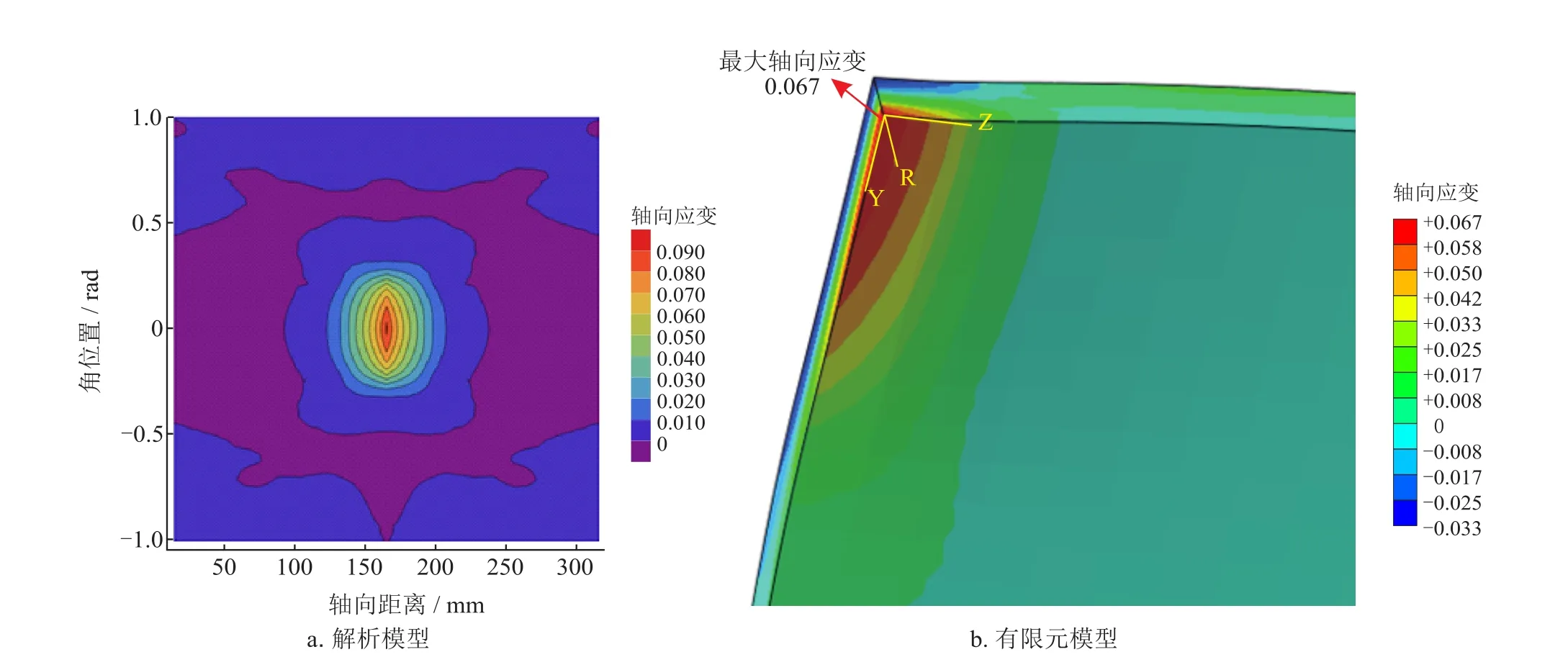
图17 解析模型和有限元模型中管内壁的轴向应变图
考虑不同等效塑性应变组合公式,由解析模型得到的等效塑性应变分布如图18所示。图18-a为不考虑剪切应变的等效塑性应变分布,图18-b为考虑剪切应变的等效塑性应变分布。
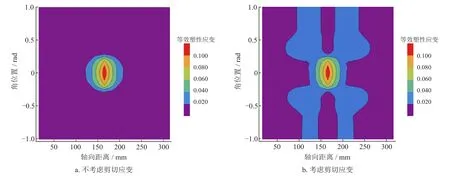
图18 等效塑性应变分布图
由有限元模型得到的等效塑性应变分布如图19所示。
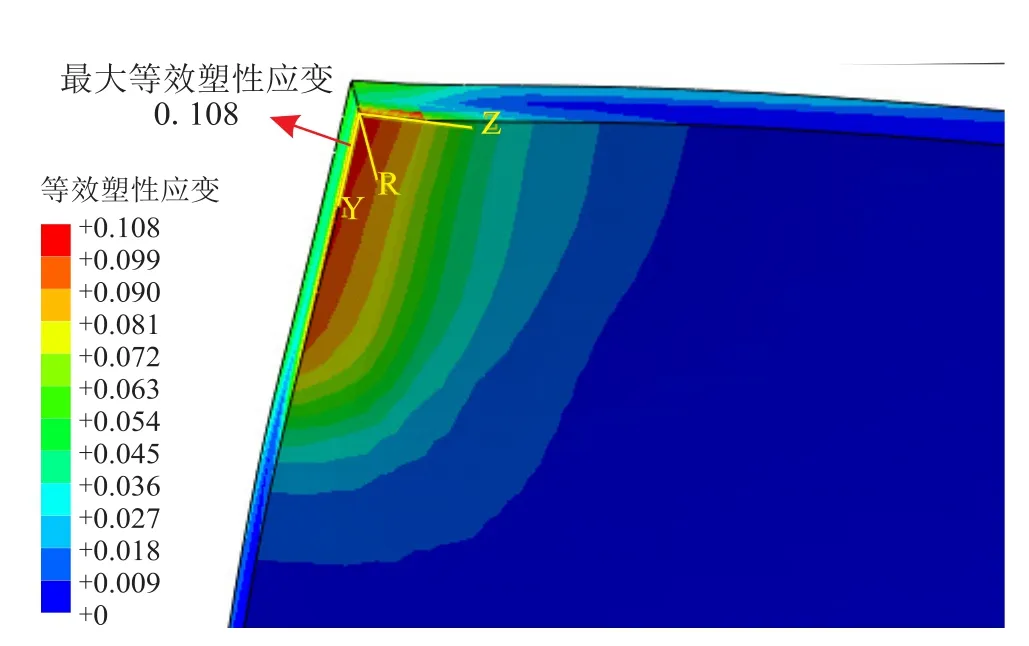
图19 有限元分析得到的管内壁等效塑性应变分布图
从图18-a可知,不考虑剪切应变时,解析模型预测的凹痕管道的等效塑性应变的最大值为0.100,位于凹痕中心。从图18-b可知,考虑剪切应变时的凹痕管道等效塑性应变最大值也为0.100,同样位于凹痕中心,但应变分布范围有所不同。对比图18-a、b,剪切应变对等效塑性应变的峰值影响较小,因此剪切应变在一般的等效塑性应变求解中可以忽略,但剪切应变会影响凹痕区域的应变分布。
从图19可知,有限元分析得到的管道内壁最大等效塑性应变为0.108,位于凹痕区域中心,有限元结果与解析模型预测结果基本一致。因此可以认为,对于非约束凹痕的总体应变评估,解析模型能很好地预测凹痕管道的最大应变值和峰值位置。
3.2 约束凹痕
将上述步骤应用于本研究中的约束凹痕,得到了相似的变形和应变结果。由解析模型得到的深度为6%D(60.9 mm)的凹痕管道内表面等效塑性应变分布如图20所示,由有限元模型得到的等效塑性应变分布如图21所示。
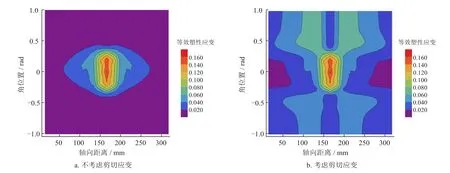
图20 等效塑性应变分布图
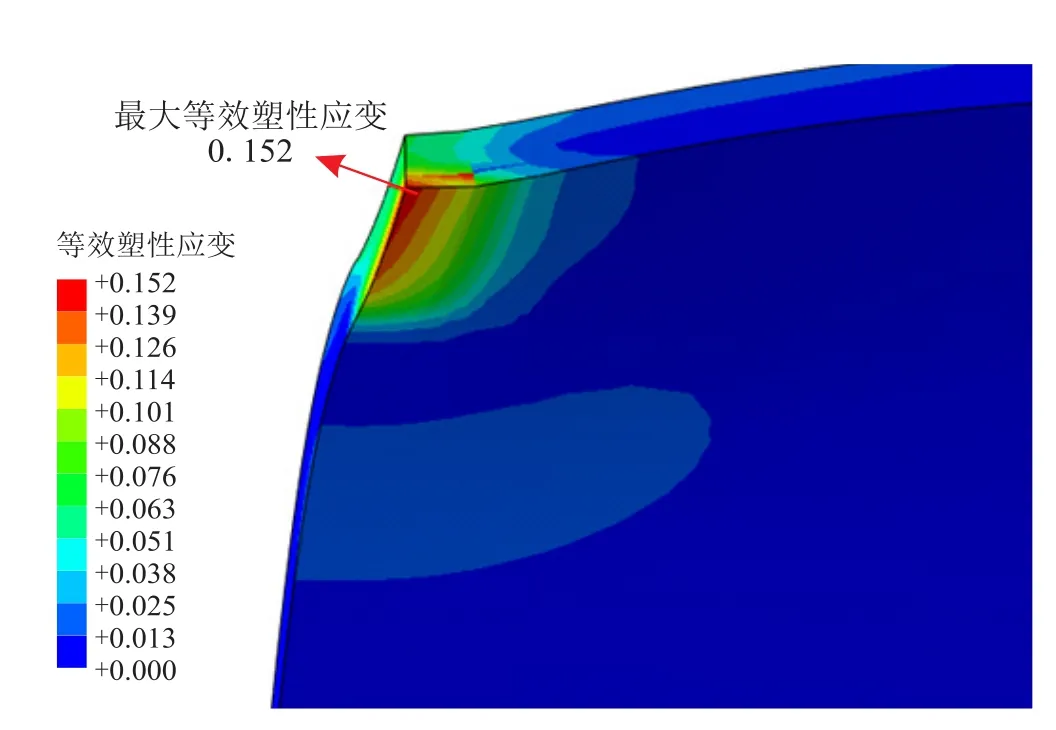
图21 有限元分析得到的管内壁等效塑性应变分布图
对比图20-a、20-b可知,解析模型预测的凹痕管道内壁的等效塑性应变的最大值均为0.160,位于凹痕中心,但应变分布范围有所不同。图21中有限元分析得到的管道内壁最大等效塑性应变为0.152,有限元结果与解析模型预测结果基本一致。因此可以认为,对于约束凹痕的总体应变评估,解析模型依然能很好地预测凹痕管道的最大应变值和峰值位置,且与文献[21]所得到的结论一致。
4 结论
1)建立了含约束型和非约束型凹痕缺陷的有压管道非线性有限元模型,分析了管道内外壁等效塑性应变沿管道轴向、环向的分布规律,结果表明对于内压作用下初始加载深度为6%D(60.96 mm)的凹痕缺陷,整个凹痕管道的塑性化程度最大点位于凹痕最深处的管道内壁,与文献所得到的结论一致,且约束凹痕的应变大于同等条件下的非约束凹痕。
2)通过对凹痕变形区域进行三维插值生成定义凹痕表面的位移函数,提出了以应变张量形式分析凹痕区域应变的解析模型,并利用该解析模型预测的应变分布与非线性有限元法预测的应变分布进行了对比,结果表明,解析模型可用来求解管道凹痕区域的应变,且能很好地预测凹痕管道的最大应变值和峰值位置。
3)通过考虑和不考虑剪切应变的等效塑性应变求解,发现剪切应变对凹痕区域等效塑性应变的峰值影响较小,因此在一般的等效塑性应变求解中剪切应变可以忽略,但剪切应变会对凹痕区域范围的应变分布产生影响。所提出的解析模型可以高效便捷地获得凹痕区域实际应变分布,为精确评价管道凹痕缺陷提供了科学依据,可用于改进现有的基于应变的凹痕评价体系。

