基于负刚度原理的低刚度及间隙模拟技术研究

徐钦炜，王 斐

航空工业成都飞机设计研究所，四川 成都 610091

引言

在颤振专业的相关地面试验或风洞试验中，低刚度支持系统作为地面共振试验（GVT）试验件的地面支持、颤振风洞模型尤其是全机颤振风洞模型的GVT 地面支持以及风洞内实现模型支持的重要机构，其提供的支持频率直接影响试验结果的准确性，关系试验成败及后续颤振分析与验证的有效性。根据飞机地面振动试验标准HB 58611984 规定，柔性支持系统的结构频率应低于试验对象最低模态频率的1/3，因此，支持系统的支持频率越低，就越能满足试验要求。

间隙广泛存在于飞机结构与机构中，外挂系统、飞行控制操纵面、起落架系统、活动舱门、全动操纵面等机构中均存在间隙，其中，操纵翼面的间隙会导致其支持刚度显著降低，从而显著降低操纵面颤振速度，使得操纵翼面颤振特性成为飞机气动弹性特性的“瓶颈”；同时操纵翼面的间隙也可能会诱发翼面极限环振荡等问题，威胁飞行安全[1]，因此，操纵翼面间隙一直是气弹专业重点关注与研究的对象。现有的含间隙结构颤振设计方法多数停留在理论分析和数值分析阶段，开展量化试验验证较少。引起该问题的主要原因是现有的颤振模型设计中，结构间隙是通过不连续的支持结构进行模拟，该方式一方面无法实现小间隙的定量模拟，另一方面将使得试验件在重力的作用下发生初始偏转，导致吹风过程中在气动力的作用下翼面始终偏转向一侧，无法保持在间隙段，从而使试验效果不佳乃至失败[2]。因此，急需一种有效定量模拟技术来设计颤振模型间隙，从而在风洞试验中模拟间隙对颤振特性的影响并为研究极限环振荡问题提供支持。

基于负刚度理论的正负刚度并联机构具有诸多优点，首先，在一定条件下，机构可以在具备很大静刚度的同时，在平衡位置附近拥有很小甚至接近零的动刚度[3]。利用这种特点，可以设计基于负刚度原理的GVT 地面支持系统。相较于传统空气弹簧，基于负刚度原理的低刚度支持系统具有更低支持频率，其值可以低于1 Hz 甚至接近零，且能根据不同试验对象灵活调整，满足不同质量特性、不同动力学特性试验对象的支持频率要求。而相比于传统弹簧绳悬挂支持方式[4]，基于负刚度原理的低刚度支持系统可以在满足极低支持频率的同时产生很小的静变形量，且不会像橡皮绳一样产生蠕变，引入附加非线性支持刚度，从而提高试验精度、减小支持系统对空间的要求。其次，在一定条件下，基于负刚度理论的正负刚度并联机构在平衡位置附近的动刚度接近零，而随着振幅增大，机构的刚度会迅速增长，并且逐渐趋近某一数值。利用这种特点，可以设计基于负刚度原理的间隙模拟装置，将小刚度区视为间隙区，将大刚度区视为非间隙区。同时，由于此机构在平衡位置附近的静刚度可以很大，因此，翼面在受气动力后容易保持在中心位置而不发生偏置，从而有效避免翼面偏置而导致试验效果不佳。

国内外学者对基于负刚度理论的正负刚度并联机构的原理和组成形式进行了广泛的研究。Tobias[5]基于不同形式的正弦弹簧设计了多种正负刚度并联机构并对这些机构开展试验，试验结果表明，该类机构在具有极低的支持频率的同时又具有良好的抗冲击性能。Platus 等[6-9]利用受压杆配合铰支联接组成负刚度元件，与正刚度弹簧在平衡位置并联后组成正负刚度并联机构，同时总结了正负刚度并联机构的特点和优势。Molynewx[10]针对两根斜向弹簧和一根竖直弹簧组成的支持系统开展了研究，Carrella 等[11]也对同样的支持系统开展了力学特性分析，通过分析提出了准零刚度（Qausi Zero Stiffness）支持系统的概念，并给出了力与位移的关系式。Zhou 等[12]使用电磁铁设计了一种负刚度机构，并用梁结构作为弹簧提供正刚度。Alabuzhev 等[13-16]通过并联线性正刚度结构和负刚度机构组成在一定的位移内具有准零刚度特性的支持系统，并对此类支持系统的力学特性进行了总结。白晓辉等[17]利用碟形弹簧本身在一定条件下可产生负刚度的原理，将其和正刚度弹簧并联，从而实现了准零刚度系统，并且通过合理选择蝶形弹簧的参数，使得在负刚度区间范围内机构的刚度变化较为平缓，有利于增加负刚度区间的范围。

通过国内外学者的深入研究与探索，基于负刚度理论的正负刚度并联机构在航天、天文、汽车、精密仪器制造、地质等行业已开展了广泛的运用。但是在航空领域，基于负刚度理论的正负刚度并联机构的应用还较少见，主要集中于某些精密机载设备的安装领域，在GVT 试验支持系统领域以及颤振风洞模型“自由—自由”边界模拟领域还未见应用的案例，而在颤振间隙模拟领域，未见国内外学者对此开展过研究。

本文通过对正负刚度并联机理进行分析，提出了一种正负刚度并联机构，开展相关试验研究，探索其在超低频支持系统以及间隙模拟系统中应用的可行性。

1 正负刚度的概念及其载荷变形关系

刚度K定义为作用在结构上的力F对力产生的变形x的导数，定义式为

一般情况下，作用在结构上的力的方向与随之产生的变形的方向相同，即系统的刚度为正值，记为Ks。在某种特殊的条件下，结构所受力的方向与随之产生的变形的方向相反，此时系统的刚度为负值，记为Kn。将具有负刚度特性的机构称为负刚度机构，该类机构在自然条件下通常不存在，需要特定的机构在一定的条件才能实现。

2 负刚度机构的实现

一种常见的负刚度机构的实现如图1，该机构由在水平方向作用有预压力的等刚度弹簧铰接而成。设图1 中弹簧刚度为Kp，弹簧原长度为L0，初始压缩量为δ，取弹簧处于水平位置为坐标原点，建立如图1 所示坐标轴。当受外界干扰铰接点产生位移x时，负刚度系统的势能Un为

图1 负刚度机构Fig.1 Negative stiffness mechanism

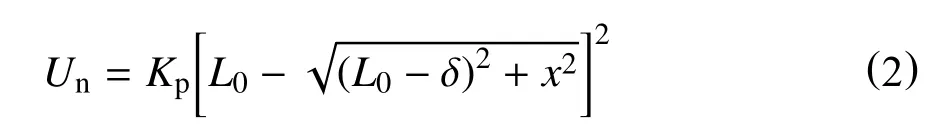
将式（2）对x求导，得到恢复力F表达式

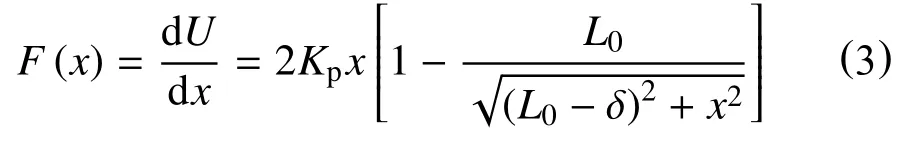
将式（3）对x求导，得到负刚度系统的刚度Kn

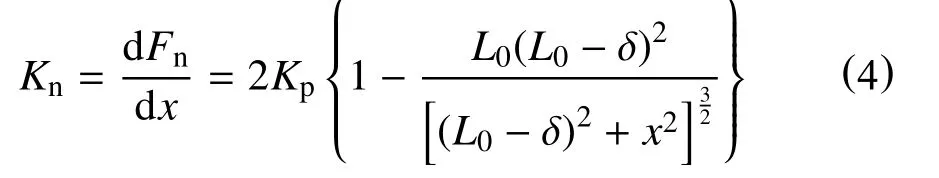
设Fc=Fn/KpL0，xc=x/L0，δc=δ/L0，Kc=Kn/Kp，代入式（3）、式（4）中，则可得到负刚度系统的无因次恢复力Fc和无因次刚度Kc的表达式

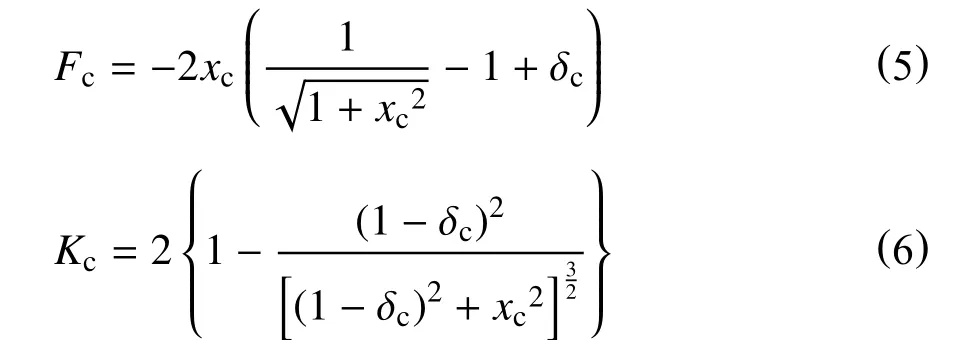
3 正负刚度并联机构原理与验证

将图1 中的负刚度机构和与普通正刚度弹簧并联组成正负刚度并联机构，如图2 所示，弹簧两端处于水平滑槽中，在水平方向可按需要滑动到一定的压缩位置。图2 中，负刚度机构的弹簧处于水平状态且未压缩，质量M垂直作用于刚度为Ks的弹簧上，弹簧压缩量为x0，即Mg=Ksx0。此时，质量M完全由正刚度弹簧支撑，支撑刚度为Ks。图3 中，在负刚度机构的弹簧两端施加初始压缩量δ，则在垂直方向产生大小为Kn的负刚度，正负刚度并联机构的总刚度为Kt=Ks-Kn。此时，正负刚度并联机构系统的固有频率为ω=实现了由刚度为Ks的支撑弹簧支撑质量M的情况下，通过调节负刚度机构弹簧的压缩量δ 使该系统的固有频率降低。

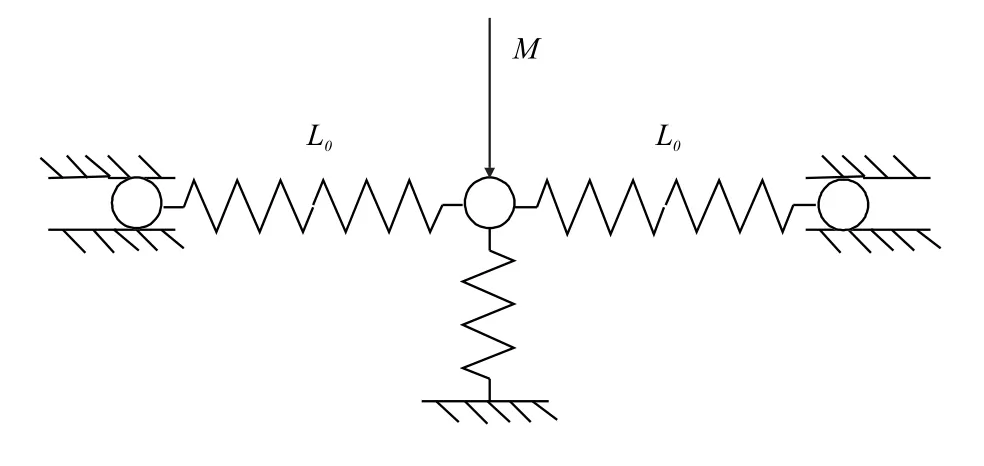
图2 正负刚度并联机构（两端弹簧未压缩）Fig.2 Parallel mechanism with positive and negative stiffness（springs at both ends not compressed）

图3 正负刚度并联机构（两端弹簧压缩）Fig.3 Parallel mechanism with positive and negative stiffness（spring compressed at both ends）

令正负刚度弹簧刚度比Ksc=Ks/Kp，结合式（5）、式（6）得到正负刚度并联机构的恢复力Ftc和刚度Ktc的无因次表达式

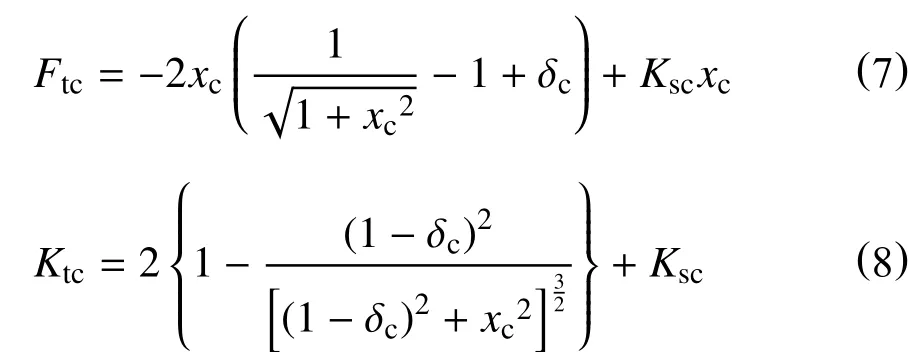
若系统在平衡位置处刚度为0，则

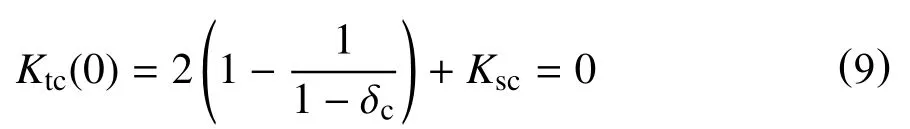
得出

将式（10）的无因次参数根据定义转化后，得

当正负刚度并联机构满足式（11）的条件时，系统在平衡位置处的刚度为零。

将式（11）代入式（8）、式（9），得到系统在平衡位置处刚度为零的条件下，不同的δc值时系统的力学特性曲线，如图4～图5 所示。由图5 可知，该系统的刚度呈明显非线性，且随着δc增大，系统在平衡位置附近的小刚度区域也越小。

图4 正负刚度并联机构力-位移曲线Fig.4 Force-displacement curve of parallel mechanism with positive and negative stiffness

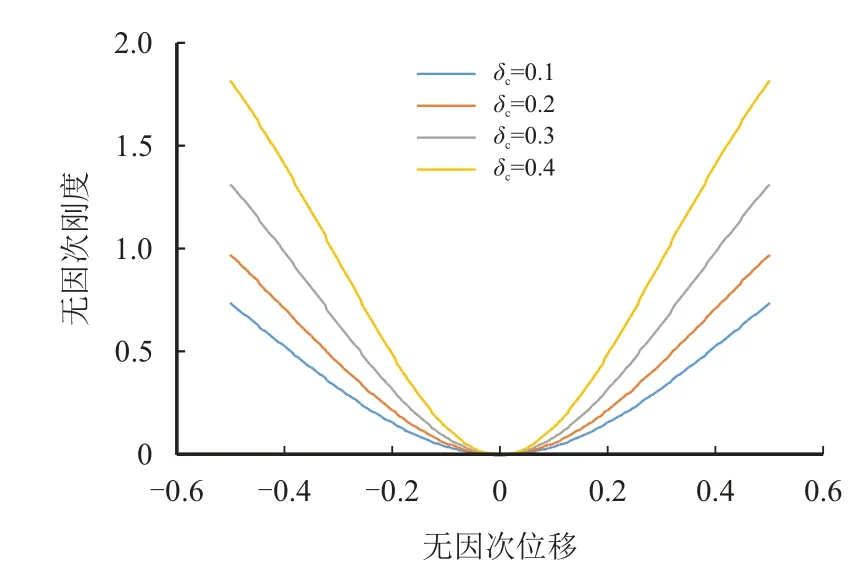
图5 正负刚度并联机构刚度-位移曲线Fig.5 Stiffness-displacement curve of parallel mechanism with positive and negative stiffness

根据上述原理，设计了一种正负刚度并联机构，并对其进行了试验研究，机构组成如图6 所示。该机构利用直线轴承、旋转轴承以及滑槽的组合，保证正负刚度并联机构的顺利实现。同时，通过各类举措尽可能减小该机构在垂直方向的摩擦力，减小了摩擦力对垂直方向恢复力的影响。

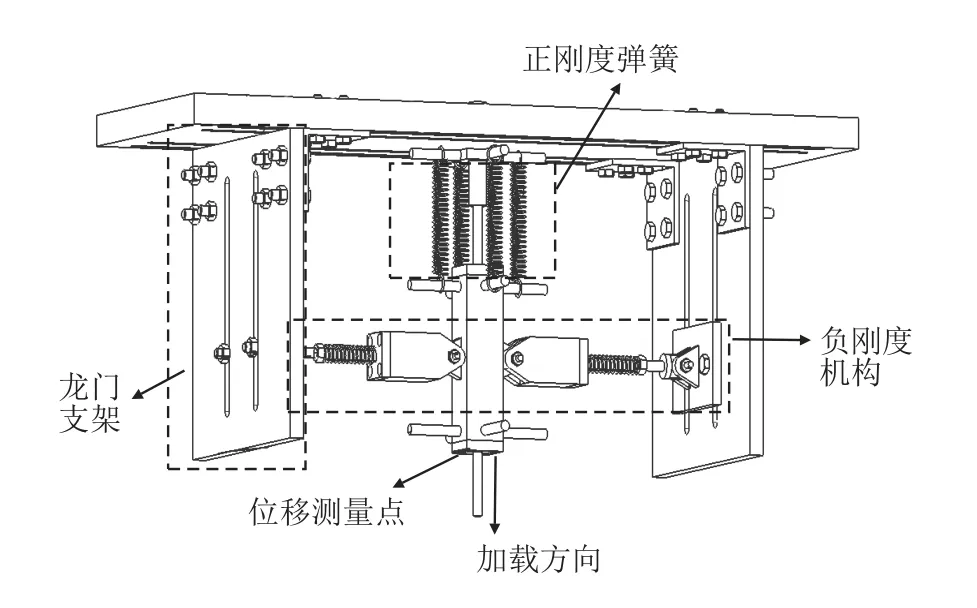
图6 正负刚度并联机构试验示意图Fig.6 Test diagram of parallel mechanism with positive and negative stiffness

试验前，根据式（11）调整负刚度结构弹簧两端的初始压缩量，使得机构在平衡位置附近的刚度为零。试验中，采用悬挂砝码的方式对机构进行加载，采用激光测振仪测量机构的垂向位移。

通过多组试验求平均值的方式，获得该系统的恢复力-位移曲线，见图7。可以看出：在平衡位置附近，系统的刚度较小，可以将该区域称为“准零刚度区”；随着变形的增大，系统的刚度逐渐上升并趋近于线性弹簧的真实刚度，可以将该区域近似看作“线性刚度区域”；与理论分析结果进行对比，试验结果与理论分析结果吻合较好，说明该理论可以指导此类机构的设计。

图7 正负刚度并联机构试验件恢复力-位移曲线Fig.7 Force-displacement curve of test piece of parallel mechanism with positive and negative stiffness

4 正负刚度并联机构的间隙模拟研究

工程结构中常见的间隙可分为中心型旋转间隙与偏置型旋转间隙两种，如图8 所示[18]。

图8 工程结构间隙类型Fig.8 Gap type of engineering structure

在实际工程中，由于摩擦等非线性因素的存在，真实飞行器的间隙测量中加载-卸载曲线存在一定的不重合，美军曾对F-22 战斗机的左襟副翼开展间隙测量，得到的典型间隙如图9 所示[19]。

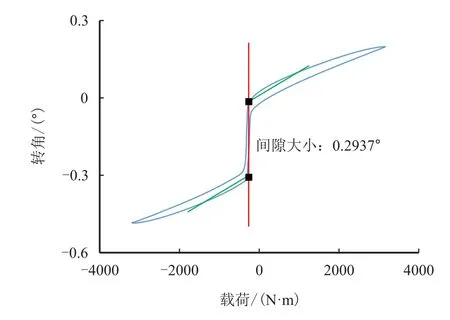
图9 F-22 左襟副翼间隙测量曲线Fig.9 Left flaperon clearance measurement curve of F-22

将正负刚度并联机构的“准零刚度区”看作是间隙段，将“线性刚度区域”看作非间隙段，则可以利用正负刚度并联机构来模拟真实飞机的带间隙机构。

根据这种思路，设计了一个基于正负刚度并联机构间隙模拟装置，用于模拟全动翼面的旋转间隙。在该装置中，通过调节Ks、Kp以及δ 的数值，得到不同的间隙尺寸，从而达到模拟真实飞行器全动翼面旋转间隙的目的。

对于试验件采用第3 节中同样的试验方法，得到该装置的加载-卸载曲线，如图10 所示。可以看出，正负刚度并联机构不仅可以有效地模拟真实结构中的间隙，还可以通过调节机构中Ks、Kp以及δ等参数的数值，调节间隙大小。

图10 间隙模拟机构的加载-卸载曲线Fig.10 Load-unload curve of gap simulation mechanism

5 结论

（1）通过对负刚度形成机理的分析与试验，证明采用负刚度结构与正刚度弹簧并联实现正负刚度并联机构是可行的，该机构的刚度在小变形下较小，在大变形下较大，呈明显的非线性。

（2）试验结果与理论分析结果一致性好，说明该理论可用于此类机构设计。

（3）设计了一个基于正负刚度并联机构间隙模拟装置并开展相关试验，试验结果表明该机构可有效模拟真实飞机全动翼面的旋转间隙，并且可通过调节参数，获得不同尺寸的间隙。

（4）正负刚度并联系统可应用于各类飞机或颤振风洞模型的GVT 试验地面支持、各类颤振风洞试验模型的刚度非线性系统模拟，以及各类型设备低刚度支持环境组建等，具有良好的工程适用性和应用价值。

符号说明

K刚度，N/m；

F恢复力，N；

x系统变形，m；

U系统势能，J；

Un负刚度系统的势能，J；

Ks系统的正刚度，N/m；

Kn系统的负刚度，N/m；

Kp压缩弹簧刚度，N/m；

L0压缩弹簧原长度，m；

Fc系统无因次恢复力；

Kc系统无因次刚度；

xc系统无因次位移；

δc压缩弹簧无因次初始压缩量；

M物体质量，kg；

Kt系统的总刚度，N/m；

ωs正刚度弹簧支持下的固有频率，Hz；

Ksc正负刚度弹簧刚度比，无因次；

Ftc正负并联机构无因次恢复力；

Ktc正负并联机构无因次刚度；

Mα外部力矩，N·m；

Kα无间隙状态旋转刚度，N（/°）；