高低刃脚异形钢围堰水力作用数值研究

唐 煜 ，杨 松，胡 攀，景 聪

1.西南石油大学土木工程与测绘学院，四川 成都 610500

2.四川公路桥梁建设集团有限公司，四川 成都 610041

引言

建设交通强国的重点任务在于建设一流的综合交通设施网络体系[1]，大型桥梁是公路和铁路跨越江、河、湖、海等自然障碍的关键节点工程。围堰（或沉井）施工是深水基础的常见施工形式，广泛应用于大型桥梁的深水桥墩建造，如沪苏通长江公铁大桥、泰州长江大桥等。围堰下沉施工过程改变了原本平衡的水体自然流态，造成复杂多变的水流环境，水流力直接作用于围堰，可能造成围堰侧翻、扭转等安全问题。2013 年10 月，重庆丰都长江二桥4 号桥墩施工过程中，水压作用导致钢围堰在隔舱混凝土顶部位置发生突然断裂。2016 年3 月，沪通长江公铁大桥29 号主墩沉井施工过程中突发大规模涌砂涌水，导致沉井靠江心侧井壁瞬间坍塌。

确定流水中围堰所受的水力荷载是围堰自身结构强度验算和整体抗倾覆抗滑移能力验算的基本前提。中国现行《公路桥涵设计通用规范JTG D602015》和《铁路桥涵设计规范TB 100022017》（简称为“公规”和“铁规”）对桥墩的水力作用都仅考虑顺流向阻力，把桥墩按截面几何差异简单归类为方形、尖端形、矩形、圆端形、圆形等5 类，通过流水压力标准值计算式中对桥墩形状系数区别取值来确定顺流向阻力，且该桥墩形状系数在公规和铁规中的取值还略有不同，从侧面反映出工程设计界对该问题的认识亟待深入。而对于横流向水力作用，公规和铁规均未考虑。当前规范对桥梁施工围堰结构的水力作用未做明文阐述，行业内围堰（或沉井）设计和施工一般直接按规范中的桥墩水力作用取值，与工程实际可能存在较大偏差，工程实践表明，桥梁围堰（或沉井）等大型结构的横向水流力较大，不可忽略，有必要开展专门研究。

水力模型试验和数值模拟是研究围堰水力作用的主要手段。王超等[2]介绍了水槽模型试验中南京长江三桥主桥南塔施工钢围堰（截面为84.0 m×29.0 m 哑铃型）所受纵向和横向水流力的作用情况；陈策等[3]基于模型水力试验测试了泰州长江大桥中塔（截面为44.1 m×58.2 m 矩形倒圆角）沉井在不同流速不同吃水深度条件组合下所受的纵向和横向水流力；胡勇等[4]通过水槽模型试验较为系统地研究了圆端形、圆形、矩形及方倒角形围堰的水流阻力和横向作用特征，研究中考虑水深、吃水深度、流速、水流夹角等影响；Kang 等[5]通过模型水槽试验测量了波浪-水流联合作用下平潭海峡大桥桥墩哑铃型围堰承受的阻力；Subrata 等[6]通过模型水槽试验研究了圆形沉井在波浪和水流联合作用下的水荷载。

水力模型试验的周期长、成本高，工程中越来越多地使用数值模拟技术对围堰水力作用进行计算分析。陈策[7]通过数值模拟研究泰州长江大桥中塔沉井的水流作用力，并与工程实测的沉井拉缆力值比较进行间接验证；胡勇等[4]通过三维数值模拟计算得到了武汉天兴洲长江大桥2 号墩施工（截面为矩形）围堰的水流阻力系数，用于指导设计；肖苡辀等[8]通过数值模拟研究常泰长江大桥5 号墩（截面为57.8 m×95.0 m 圆端形）沉井在不同下沉深度下的水力特性，所得水流阻力系数与模型水工试验结果吻合较好；魏凯等[9]利用CFD 软件分析考虑开挖基坑影响下，某跨越长江的双塔斜拉桥主塔（截面为95.0 m×57.8 m 圆端形）沉井下沉过程中的水流力变化；段伦良等[10]使用CFD 模拟分析了某大桥桥台施工（截面为37.8 m×84.8 m 哑铃形）围堰周围流场的分布特点及周围海床的局部冲刷形态。

上述研究在一定程度上为工程中的围堰水荷载取值提供了参考依据，但这些研究均基于围堰（或沉井）刃脚齐平的平底情况，仅适合河床较为平缓的工程地址场景。当桥墩处于基岩倾斜角度较大的河床，高低刃脚异形围堰（或沉井）更加适用，如南龙铁路闽江特大桥10 号墩和17 号墩、忠县长江大桥8 号墩等均采用此类异形围堰施工建造。相比于水流对平底围堰的水力作用，高低刃脚异形围堰绕流流场更为复杂，其横流向力可能更大，设计难度增加，目前还未见到有关高低刃脚异形钢围堰水力作用的相关研究报道。

鉴于此，本文以河道中某大跨度桥梁工程桥墩施工采用的高低刃脚异形钢围堰为研究对象，通过求解流体运动的雷诺时均Navier-Stokes 方程（RANS）和SSTk-ω 湍流模型，模拟围堰下放过程中的典型阶段，分析围堰绕流场特征，研究流水作用下的围堰阻力与侧向力特性。

1 异形围堰工程概况

某围堰服务于跨江大桥基础施工，根据该处河床线高低起伏的特点，设计为高低刃脚异形钢围堰，如图1。

图1 河道中的围堰Fig.1 Cofferdam in river channel

围堰采用圆形截面，直径D为41 m，根据施工需要，围堰在下沉前其内部区域的河床上已安装就位19 根直径为3.3 m 的圆柱形钢护筒用于下沉定位。异形围堰最大高度16 m，最小高度9 m。以设防水位为研究水位，围堰下沉到达预定位置后，围堰最低处距设防水位为16 m。

2 围堰绕流数值模拟

2.1 水流控制方程及湍流模型

河道水流可视为不可压缩流体，其雷诺时均的Navier-Stokes 方程可表示为

涡动黏性由SSTk-ω 模型来计算，该模型中的k方程和ω 方程分别为

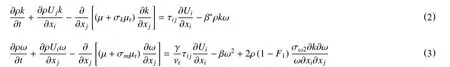
2.2 重叠网格技术及计算域网格划分

重叠网格又称嵌套网格，是一种允许网格子区域相互重叠嵌套的结构网格方法，各个子网格之间的流场信息通过插值传递。重叠网格技术最初由Benek 在1985 年提出[11]，随着其发展完善已作为计算模块嵌入一些商用CFD 软件，近年来逐步应用于模拟工程实际中的运动边界问题，如飞机水上降落[12]、物体入水[13]、多部件飞行器气动分析[14]等。本研究采用重叠网格技术对计算域进行离散，实现围堰下沉各个阶段的快速建模分析，河道水流中的围堰绕流场求解在基于有限体积法的计算流体动力学软件FLUENT 平台上进行[15-17]。重叠网格建模与常规计算中仅需一套固定网格的建模有所不同，其需准备前景网格和背景网格两套网格，为减少计算误差，两套网格在空间重叠区的尺寸应尽量保持一致[18-20]。重叠网格可实现传统动网格功能，不必担心出现负体积，还可对复杂模型进行拆分，分别布置于前景网格及背景网格中，方便物面网格的结构化划分，降低数值模型的空间离散误差。

在数值模拟过程中，河床横断面地形起伏不容忽视，由于缺乏天然河道上下游地理高程数据，此处以设计水位条件下围堰工程位置所在的河道过流断面为几何建模基本面，沿法向水平拉伸成体建立计算域。为降低计算域边界条件的不利干扰，计算域上游入流面距离围堰约20D，下游出流面距离围堰约60D，流场最大水深约为19 m，如图1b 所示。

将包含19 个定位钢护筒的河道整体流体域划分网格并作为背景网格，将仅单独包含钢围堰的局部水体区域划分网格并作为前景网格。计算域采用高质量六面体网格进行空间离散，并对围堰下放区域内进行网格加密布置，对异形围堰、护筒及河床表面铺设边界层网格以期更准确地捕捉壁面力，在距离围堰较远区域采用较稀疏的网格布置以节约计算资源。

图2 为前景网格与背景网格在FLUENT 软件内的装配情况，数值模型网格总数量约170 万。

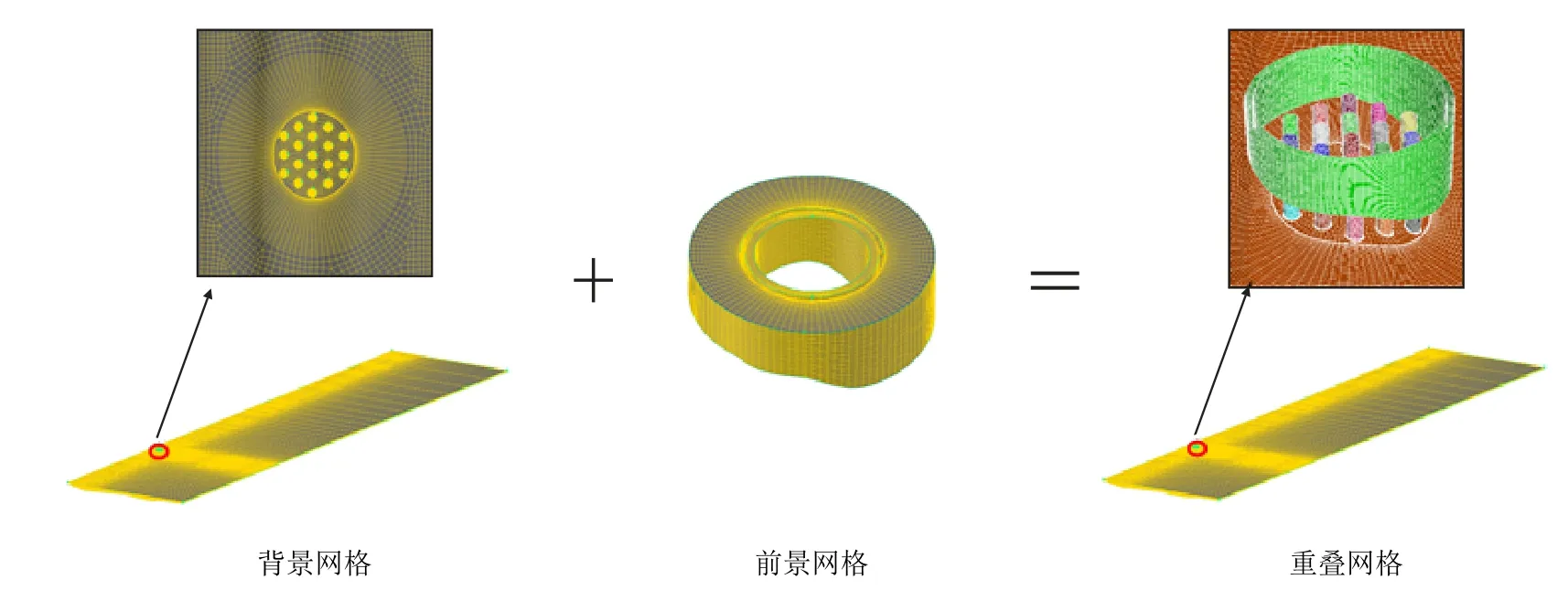
图2 计算域重叠网格划分Fig.2 Overlap meshing of computational domain

2.3 边界条件及模型参数设置

出于简化问题的考虑，河道围堰绕流流场模拟中忽略波浪和雍水的影响，对河流自由水面采用动刚盖假设[21-23]，设置为对称边界条件。围堰表面、河床壁面及护筒壁面，均为无滑移壁面。计算域下游出流边界为压力出口，上游入流边界为速度入口。由于缺乏河道比降和河床壁面粗糙度等基本参数，无法确定天然河道的流速分布，本研究将入流边界处简要考虑为均匀入流。采用定常计算，数值迭代步数为3 000，压强和速度求解算法为Coupled。在FLUENT 软件耦合计算中，Courant 数描述时间步长与空间步长的相对关系，合理设置Courant 数可以在保证求解稳定的前提下加速收敛，本研究经过试算，将Courant 数取为50，这样可兼顾效率和稳定。

数值模拟在两台具有16 核心CPU 主频3.8 GHz，内存48 GB 的计算工作站上进行。研究工况包括无围堰及围堰下沉至2，4，6，8，10，12，14 和16 m 共8 个典型入水深度情况；河道上游来流分别考虑4.5，5.0 和5.5 m/s 共3 个流速，总计27 个计算工况。

3 结果分析

3.1 围堰水流力

侧向力系数与阻力系数是对围堰所受水流作用力的无因次化，三维情况下，侧向力与阻力系数定义为

式中：

Cl侧向力系数，无因次；

L侧向力，N；

Q动压，Pa；

S参考面积，此处取围堰入水部分顺流向投影面积，m2；

Cd阻力系数，无因次；

D′阻力，N。

图3 所示为计算所得围堰水流力（阻力和侧向力）及其系数。

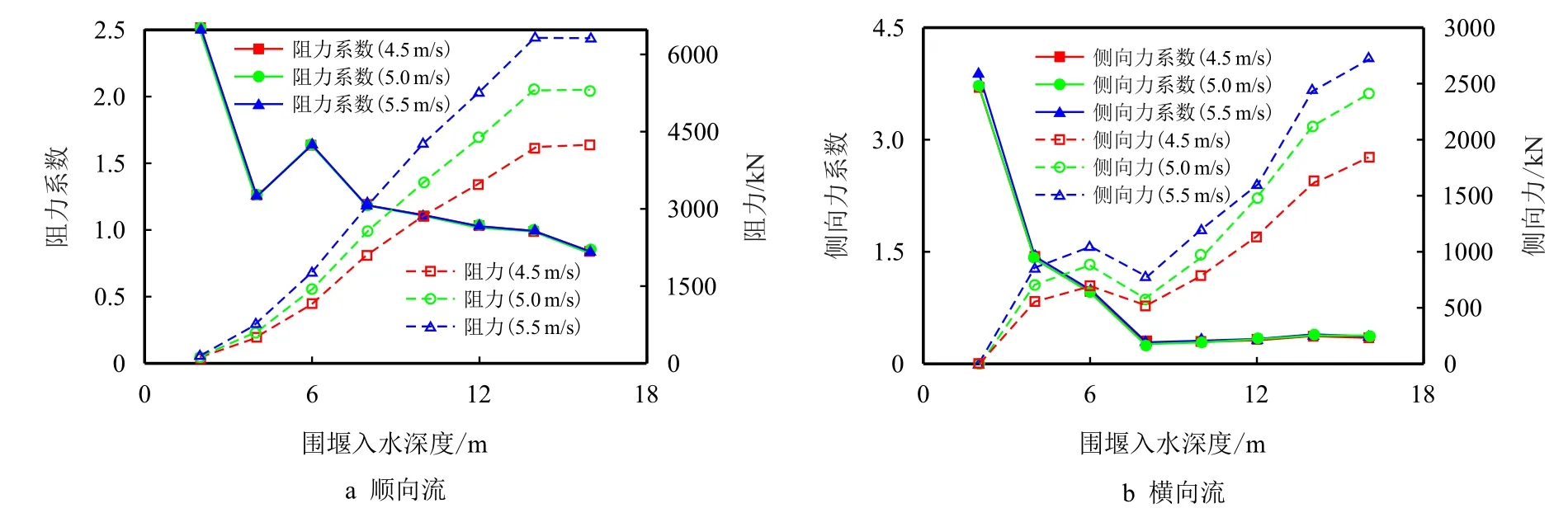
图3 围堰水流力Fig.3 Flow forces on cofferdam

从图3 可以看出，改变来流流速对无因次化的侧向力系数及阻力系数几乎无影响。围堰在入水深度0～8 m 的侧向力系数及阻力系数变化显著，这与围堰高低刃脚对应的异形区段高度吻合，异形区段围堰复杂几何外形在不同入水深度情况下对应着阻水面积非常规变化。因近河床区域流速较河面相对更低，在围堰接近触底时，其阻力和侧向力随入水深度增加均有变缓趋势。

同一深度条件下，围堰侧向力与阻力系数几乎不因流速变化而变化。侧向力及阻力随流速增大而增大，入水深度越大，这一现象越明显。在同一来流流速条件下，CFD 计算的围堰阻力随入水深度增加而增大。

3.2 围堰表面压强及周围流场迹线

河道来流为5 m/s 时，4 个典型工况下护筒与围堰表面压强分布及周围流场迹线见图4。

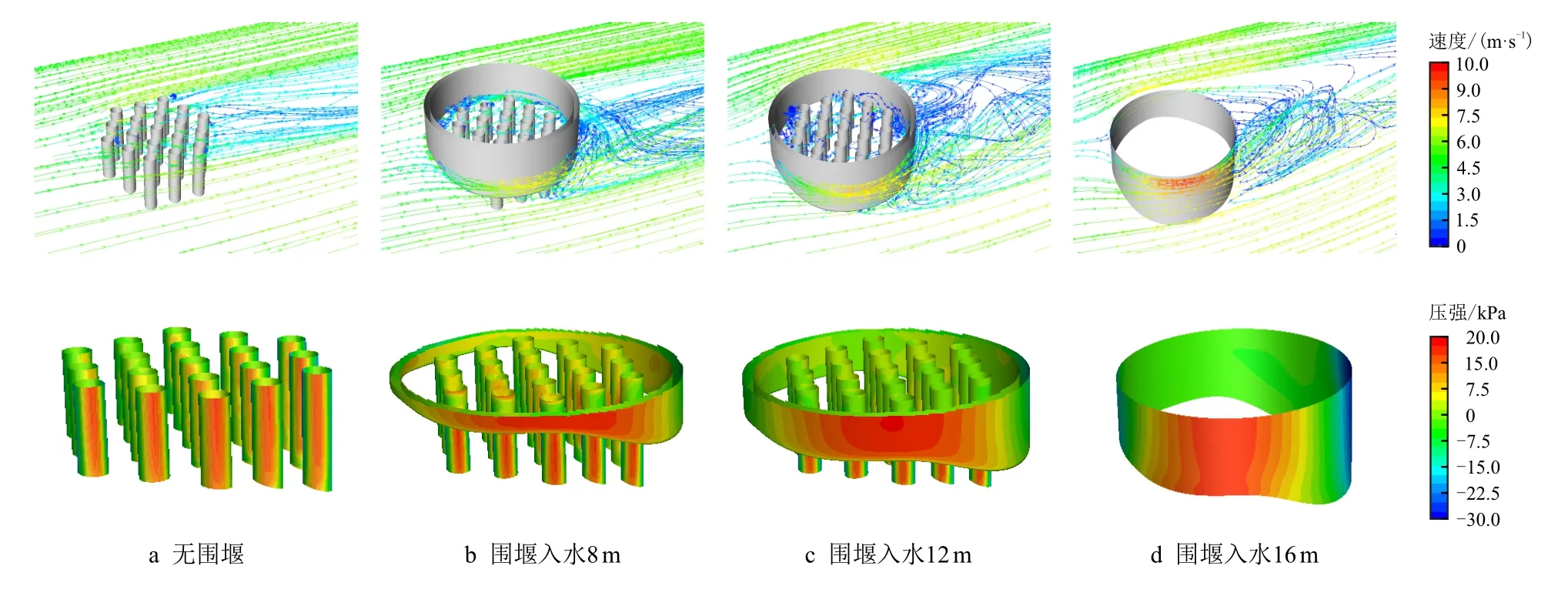
图4 围堰表面压强及迹线分布Fig.4 Pressure and trace distribution of cofferdam body

其中，无围堰工况及围堰入水16 m 工况是施工过程中持续时间最长的两个阶段。围堰下放初期，护筒为该施工区域主要的障碍物，流体因护筒存在而发生局部加速。随围堰下放深度增加，作用于迎流面护筒表面最大正压区逐渐下移。在迎流面围堰底部护筒区域，河道水体受护筒与围堰约束作用，产生上切水流，这部分水流易造成护筒内部水体涌动；堰尾区域存在两个大尺度漩涡，深水侧堰尾漩涡区较为明显，且远大于近岸侧漩涡，漩涡区域内平均流速均远小于围堰上游来流流速。

3.3 压强与速度分布

取围堰入水深度12 和16 m（触底）两个典型工况，围堰触底后内部区域不再计入流体域，水面以下2，6 和10 m 围堰周边流速及压强水平切片见，如图5、图6 所示。围堰附近水流存在局部加速，其最大速度出现在围堰两侧，河心侧流速受围堰影响明显大于近岸侧，该加速效应沿流向逐渐减弱，且水体越深的区域加速效应越弱；最大正压区域出现在围堰迎流侧，围堰触底工况中可明显观察到最大负压在围堰河心侧。

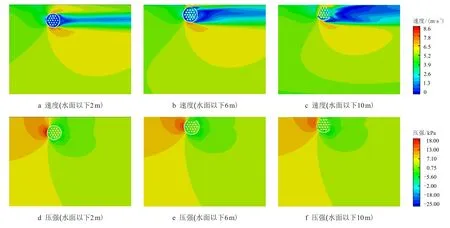
图5 速度和压强分布（入水深度12 m）Fig.5 Velocity and pressure（underwater 12 m）

图6 速度和压强分布（入水深度16 m）Fig.6 Velocity and pressure（underwater 16 m）

3.4 围堰内外湍流强度

以河道来流5 m/s 流速为例，绘制围堰周边及内部湍流强度分布（图7）。围堰附近湍流强度高于远离围堰的河道主流区，湍流强度在围堰内部及两侧底部存在较大变化。最大湍流强度出现在堰尾区域，沿河道流向逐渐减小，且深度递增呈减弱趋势。

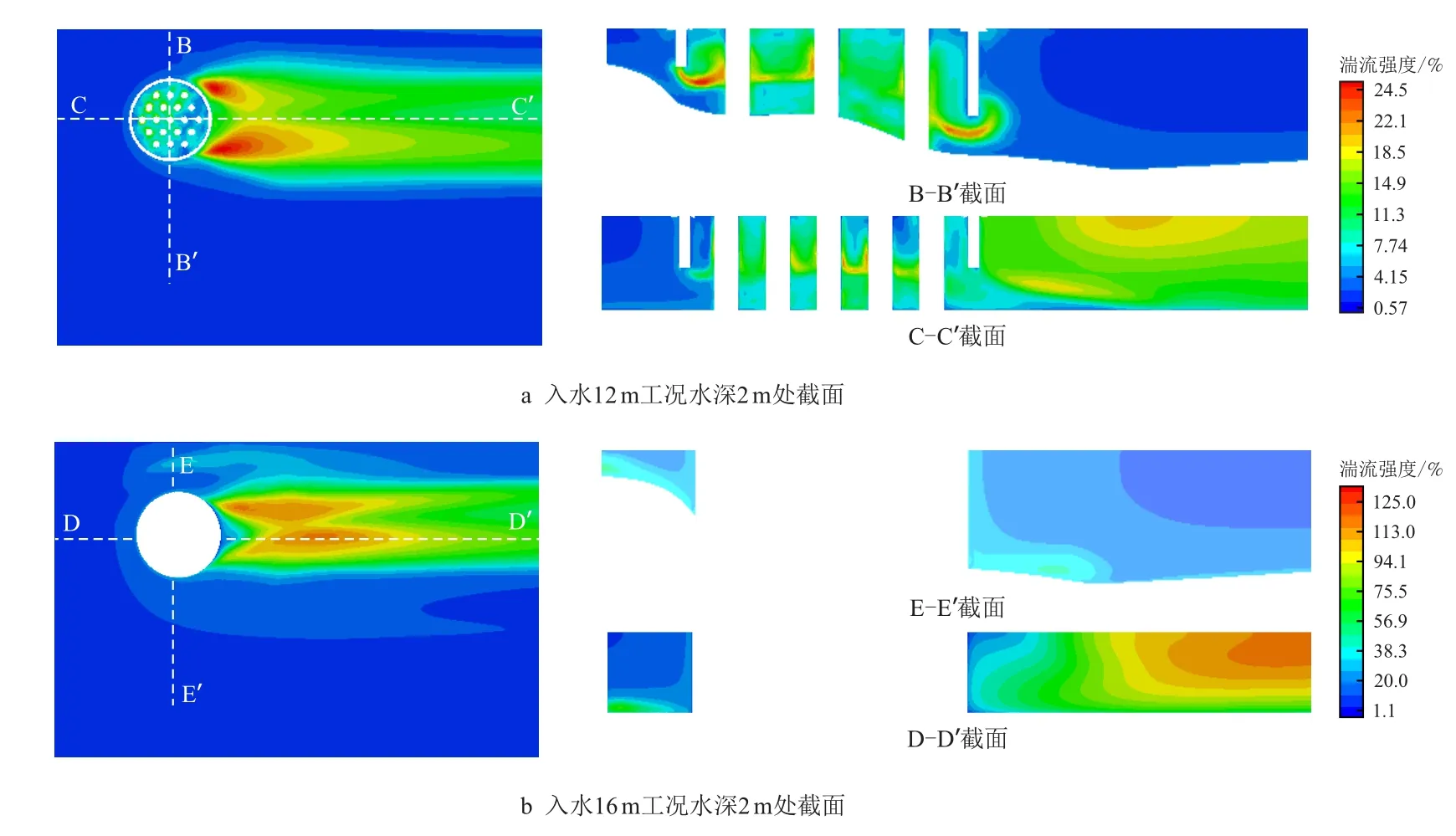
图7 湍流强度分布（围堰入水12 m 及16 m）Fig.7 The turbulence intensity（underwater penetration 12 m and 16 m）

围堰入水16 m 时堰尾最大湍流强度较围堰入水12 m 时大幅增强，原因可能在于堰下水流通道封闭，主流对堰尾大尺度旋涡的能量输入增强，该特征对河床底面冲刷存在不利影响，施工时应加强监控。

4 结论

（1）重叠网格的使用，使得复杂模型生成结构化网格更为简单，一套网格可进行多个工况模拟，提高了建模效率和物面网格质量。

（2）受护筒及河床影响，高低刃脚异形钢围堰两侧流速呈不对称分布，深水侧速度出现大面积加速，且随水深的增加流速逐渐降低。

（3）湍流强度最大区域出现在堰尾漩涡区，其强度值受顺流向位置及深度影响。

（4）围堰侧向力系数与阻力系数对河道来流流速不敏感。