高强钢丝蚀坑尺寸对应力集中效应的影响

吴梦雪，尹 力，唐德发

西南石油大学土木工程与测绘学院，四川 成都 610500

引言

自1823 年首座用冷拔铁丝构成缆索支承的永久性桥梁在日内瓦建成，索承式桥梁结构迈入了新的篇章，其在跨径200～2 000 m 及以上（覆盖了90%的跨径范围）都具有很强的竞争力，因此在全世界范围内得到了迅猛发展。然而大量的既建桥梁投入使用，也带来了新的挑战。拉（吊）索是由若干根钢丝所组成，而索承式桥梁常横跨大江、大河、海湾、峡谷地区，地理位置和气候条件均较复杂，桥梁从施工建设到投入使用都持续受到周围环境腐蚀的影响，如：北方的冻害及冰盐、南方的酸雨及湿热、沿海的盐雾、城镇区车辆的尾气、工业区的工厂腐蚀性废气等都是造成拉（吊）索腐蚀损伤的环境因素，使得桥梁拉索内的钢绞线发生严重腐蚀，降低桥梁的承载能力。钢丝的腐蚀类型可分为均匀腐蚀和局部腐蚀，而由局部腐蚀中的点蚀所形成的蚀坑会严重威胁钢丝的使用寿命[1-3]。因此研究锈蚀钢丝的疲劳问题非常重要。

目前，大量学者针对拉索及钢丝的锈蚀问题进行了相关研究。Nakamura 等[4]对镀锌钢丝腐蚀疲劳强度进行了实验研究和和有限元分析，结果表明，腐蚀等级越高，发生的蚀坑往往也越深，在三级腐蚀环境下，最大深度为0.56 mm。Li 等[5]在实验室内进行了高强度钢丝的加速腐蚀试验，得到了高强度钢丝均匀腐蚀的特征，并建立了均匀腐蚀深度的时变模型。黄小光[6]利用双变量半椭圆点蚀模型，建立腐蚀疲劳点蚀演化及裂纹成核的二维模型，导出点蚀形状参数随点蚀深度的演化规律。秦广冲等[7]利用有限元软件ANSYS 研究了平面蚀坑的应力集中系数与其三维蚀坑尺寸的关系。兰成明等[8]通过试验系统地研究了服役18 年换下的腐蚀斜拉索的腐蚀疲劳性能，结果显示腐蚀会严重缩减斜拉索的钢丝疲劳寿命。叶华文等[9]根据临界域法，采用精细有限元法建立了钢丝腐蚀疲劳寿命预测模型，并将疲劳试验获得的3 种形状腐蚀坑钢丝的疲劳寿命与预测的疲劳寿命结果相对比。孙传智[10]以袁州大桥拆下来的吊索为研究对象，采用断裂力学对其腐蚀疲劳寿命进行评估。姚国文等[11]为研究拉索镀锌钢绞线的腐蚀疲劳现象开展了人工加速腐蚀试验，并讨论了不同加载方式对腐蚀的影响，试验发现受到交变荷载的构件在同等的腐蚀环境中更易遭受腐蚀。Zheng[12]等以某拱桥上服役13 年的吊杆中的腐蚀高强钢丝为研究对象，通过疲劳试验得到了腐蚀钢丝的力学特性和断裂特征，结果表明腐蚀钢丝的延性随腐蚀程度的增加而急剧下降，点蚀尺寸与疲劳寿命之间的负相关性会随着应力范围的增大而减弱。王瑞雪[13]通过调研吊索截面钢丝腐蚀程度分布情况、吊索钢丝的腐蚀速率以及腐蚀钢丝的S-N 曲线，提出其腐蚀疲劳寿命的计算方法。冯小敏[14]根据悬索桥骑跨式吊索与外界环境中腐蚀介质接触的先后顺序及吊索损伤演化破坏的先后顺序，将吊索钢丝的腐蚀疲劳全寿命分为4 部分，并分别计算吊索腐蚀疲劳在这4 个阶段的生命周期，从而得到吊索的腐蚀疲劳寿命。乔燕等[15]基于断裂力学对吊索钢丝腐蚀疲劳寿命开展了研究，把吊索镀锌钢丝腐蚀疲劳裂纹形成和扩展过程分解成镀锌层腐蚀失效、蚀坑萌生、蚀坑形成、短裂纹扩展、长裂纹扩展和断裂破坏等阶段。

蚀坑对高强钢丝力学性能的影响主要体现在蚀坑处出现的应力集中现象。根据上述文献可将锈蚀钢丝力学性能的研究方法分为3 种：（1）通过人工加速腐蚀试验等手段模拟钢丝腐蚀环境，然后对其进行承载力试验；（2）采用实际工程换下的索体里的高强钢丝作为实验样品并进行承载能力试验；（3）根据高强钢丝的材料参数以及材料本构关系，进行有限元仿真模拟。通常前两种方法存在极难控制钢丝的锈蚀程度、蚀坑形状和难以获得大量实验样品的问题，因此，本文采用数值模拟的方法进行研究。过去涉及蚀坑的研究大多局限于平面蚀坑的情况，鉴于此，本文从三维蚀坑的角度探讨了蚀坑的长、宽、深对高强钢丝应力集中效应的影响。

1 钢丝腐蚀机理

钢丝的力学性能对腐蚀极为敏感，腐蚀使钢丝表面产生的蚀坑会导致应力集中，削弱钢丝局部的疲劳抵抗能力，从而吸引疲劳裂纹从这里成核，并因应力集中加速了疲劳破坏的裂纹萌生与扩展。当锈蚀钢丝处于冲击荷载、循环交变荷载作用下时，将产生腐蚀疲劳现象，使材料疲劳强度大幅降低，这通常是斜拉桥拉索承载力和使用寿命降低的直接原因。因此，研究锈蚀钢丝的腐蚀机理具有重要意义。

1.1 钢丝锈蚀基本原理

由于桥梁服役环境以及工况的复杂性，拉索钢丝有时会暴露于腐蚀性环境中，钢丝表面的金属层与腐蚀介质发生的电化学反应导致它有可能发生不同形式的腐蚀。通常，一般腐蚀可由物理和电化学措施得到很好的限制或防止钢丝表面金属层与腐蚀介质发生电化学反应，而对局部腐蚀的演变仍然是难以控制的。其中，点蚀是金属和合金结构中典型的破坏性局部腐蚀形式，它会引发结构部件的加速开裂，是导致构件失效的重要因素之一。

1.2 腐蚀类型

斜拉桥拉索钢丝在腐蚀性介质中可能出现4种锈蚀：均匀锈蚀、点蚀、应力腐蚀开裂以及腐蚀疲劳[16]。（1）均匀锈蚀属于较为常见的腐蚀类型，常发生于钢丝表面镀锌层，使钢丝截面减小，降低钢丝的承载能力。（2）点蚀是在均匀锈蚀程度较深时，在构件的某点或者生产造成的缺陷处，局部聚集了大量活化阴离子（例如氯离子），与钢丝表面的氧化物共同促进了电化学反应的发展，从而在局部发生点蚀。点蚀所造成的蚀坑不仅削弱了钢丝截面，还会在蚀坑附近引起应力集中。（3）应力腐蚀是由应力与腐蚀介质耦合所引起的腐蚀现象。应力腐蚀会使材料在低于其屈服极限的拉应力作用下发生脆断。（4）腐蚀疲劳是指腐蚀介质与循环应力的耦合作用下发生的断裂现象，相较于应力腐蚀具有更快的裂纹扩展速度。腐蚀疲劳的发展常分为两个阶段，即裂纹萌生与裂纹扩展。有研究表明，腐蚀疲劳裂纹萌生寿命占总寿命的10%，裂纹扩展占总寿命的90%，构件的腐蚀疲劳寿命主要由裂纹扩展速率控制[17]。

2 有限元建模

受腐蚀介质的影响，钢丝表面会产生形状不一的蚀坑，而为了评估蚀坑形状对钢丝力学性能的影响，可将蚀坑模拟为半球形缺口，为更贴近真实形状，可模拟为半椭球形状[18-19]。本文用半椭球空腔模拟钢丝表面蚀坑。

2.1 单元选择

本文采用有限元软件ANSYS 15.0 建立了锈蚀钢丝的实体模型，需要采用能适合曲线边界的单元。本文拟选用SOLID 95 和SOLID 186。SOLID 95 能够容许不规则形状，并且不会降低精确性，而SOLID 186 具有同样的适用性并且有更高的精度。但考虑到蚀坑处的网格划分是比较精细的，若采用SOLID 186 单元，则会大大降低计算效率。通过试算，发现SOLID 95 基本满足了求解精度需求，因此本文最终选择SOLID 95 单元建立了锈蚀钢丝的实体模型。

2.2 模型建立

斜拉桥拉索在服役中受到各种复杂荷载作用，但最主要还是受到轴向拉力作用，因此本文仅考虑钢丝轴向受拉这一受力状态。为了保证钢丝始终处于线弹性阶段，轴向均布面荷载取值应不高于材料极限强度的30%，因此在有限元模拟中，在钢丝一端施加500 MPa 的轴向面拉应力，另一端固定，如图1 所示。有限元建模时，采用直径为7 mm 的圆柱体模拟钢丝，为避免边界条件对蚀坑应力分布造成影响，将蚀坑位置建立在钢丝中部，钢丝实体模型长度取20 mm。模型基本参数如表1 所示。

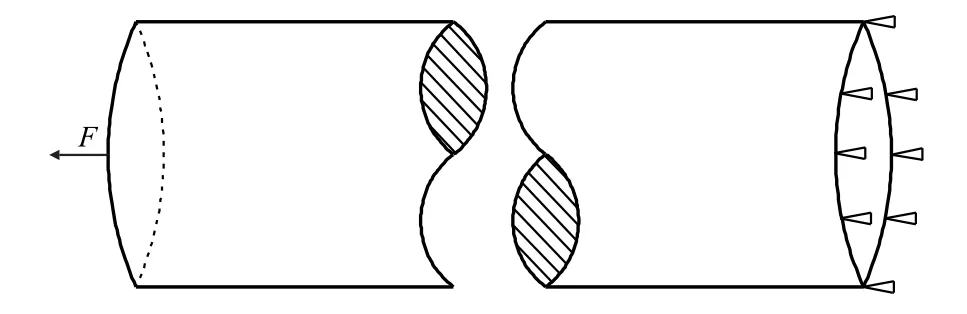
图1 边界条件与加载方式示意图Fig.1 Schematic diagram of boundary conditions and loading method

表1 钢丝模型基本参数Tab.1 Key parameters of finite element model

在实际工程中，腐蚀环境会使钢丝表面产生不同形状的空腔[20]，Godard 等[21]通过观察铝合金在水下的蚀坑演变后认为，蚀坑在各方向都以相近的速度增长，并提出用半球形空腔模拟蚀坑形状；Harlow 等[22]和Chen 等[23]根据实验观察提出，采用半椭球形空腔模拟蚀坑形状。虽然蚀坑形状不尽相同，但通常用于表示蚀坑的几何形状的参考参数是深度，宽度及长宽比，因此，相关研究也常用最简单的半球形或者弹壳形来模拟蚀坑形状[24-25]。本文基于上述文献研究，采用更贴近实际工程中蚀坑形状的半椭球形空腔来模拟蚀坑形状，通过长、宽、深定量控制蚀坑形貌来研究蚀坑形状对应力集中系数的影响。钢丝蚀坑形貌如图2 所示。

图2 钢丝蚀坑立面图/钢丝蚀坑断面图Fig.2 Elevation diagram of corrosion pit of steel wire/Cross-sectional diagram of corrosion pit of steel wire

2.3 网格划分

对于有限元模型，网格划分的形状和精密度直接影响到计算结果的准确性及计算效率，因此合理的网格密度是有限元数值模拟的重要前提。为综合考虑网格密度和计算规模，一般认为最大单元应力和最大节点应力的比值达到95%时网格划分密度合适，计算结果可信。

在网格单元形状的选择上，六面体单元相较于四面体单元具有更高的计算精度，但难用于蚀坑处的网格划分，因为在蚀坑细节处容易出现不规则形状的单元，从而影响计算结果的准确性。最终选取四面体单元形状进行网格划分，通过减小单元尺寸来保证计算精度。

在单元尺寸的选择上，对蚀坑处的网格划分进行局部加密，本文选取4 种网格尺寸进行试算，分别对比计算结果精度和计算时间成本。对靠近钢丝端部区域的网格尺寸取0.3 mm，靠近蚀坑处的区域网格尺寸分别取0.05～0.20 mm。计算结果如表2所示。

表2 不同网格精度下最大单元应力与最大节点应力对比Tab.2 Comparison of maximum element stress and maximum node stress under different mesh

网格精度为0.10 和0.05 的最大单元应力与最大节点应力的比值都分别为96.03%和97.93%，都能满足网格划分合理性的要求，对比两种网格精度所需的计算时间代价，结果发现相差不大。因此，经过综合考虑，本文最终在蚀坑处选择0.05 mm 的单元尺寸。网格划分示意图如图3 所示。

图3 网格划分示意图Fig.3 Mesh of the finite element model

3 计算分析

蚀坑处产生的应力集中程度可用彼得森应力集中系数来描述。应力集中系数由蚀坑处最大应力与该处名义应力之比得到，即

名义应力是不考虑缺口引入的应力集中，而按净面积计算获得的平均应力。

通过有限元软件ANSYS 15.0，建立了若干组不同尺寸比例的钢丝蚀坑模型，分析蚀坑处的应力分布规律，研究蚀坑形状对应力集中系数的影响趋势，拟合出应力集中系数随蚀坑尺寸的变化公式，量化对比蚀坑的3 个尺寸的影响程度并以此判断最危险蚀坑形状。

3.1 长度变化对应力集中系数的影响

结合图2，在研究长度的影响时，控制蚀坑的宽，深度不变，通过改变长宽比来探究蚀坑长度变化对应力集中系数的影响。根据设置3 种不同深度的工况来验证变化规律的准确性。

图4 是蚀坑深度0.3 mm，长宽比取0.4、0.6 和0.8 时的应力云图。

从图4 应力云图结果可以看出，由于应力集中效应使得高应力区呈带状分布于蚀坑的中部，其中最大应力都出现在高应力区沿宽度方向的边缘。最小应力值则位于沿长度方向上的蚀坑口。由应力分布变化情况可知，随着长宽比的增加，蚀坑处整体应力值呈下降趋势，并且分布于蚀坑底部的高应力带带宽明显增加。这说明随着长度的增加，蚀坑形状逐渐由细窄形变为宽浅形，并且蚀坑内部的高应力带分布区域发生扩散，使得更难引起高应力集中，这一现象与应力集中系数的变化趋势相一致，因为应力集中系数反映了应力集中的程度。

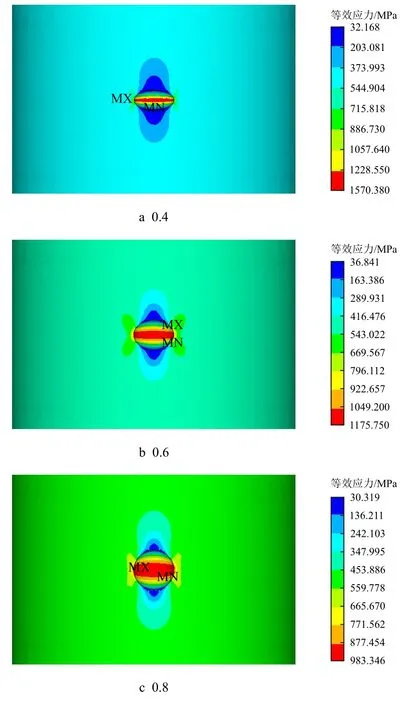
图4 不同长宽比下0.3 mm 深蚀坑的应力分布Fig.4 Stress distribution of 0.3 mm depth pit under different aspect ratio

3 种深度（0.3，0.4 和0.5 mm）蚀坑的应力集中系数与长宽比的关系见图5。

图5 应力集中系数随长宽比的变化规律Fig.5 Stress concentration coefficient varying with different aspect ratio

分析图5 可得，当蚀坑宽度及深度不变时，应力集中系数随长度的增加而减小，应力集中效应有所减弱，这一现象有利于带蚀坑或缺陷构件的后续服役。同时，根据图5 拟合出3 种深度下的公式具有相同的变化趋势，进一步验证应力集中系数随长度的变化规律：应力集中系数随着长宽比的增加，下降速度明显减缓。采用二次函数进行拟合可得

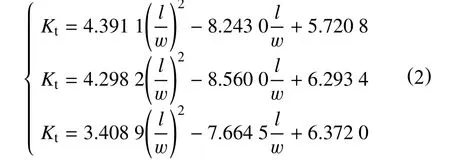
3.2 宽度变化对应力集中系数的影响

在研究宽度的影响时，控制蚀坑的长、深度不变，通过改变宽深比来探究蚀坑宽度对应力集中系数的影响。根据设置3 种不同深度的工况来验证变化规律的准确性。图6 是蚀坑深度0.3 mm，宽深比取0.4、0.6 和0.8 时的应力云图。

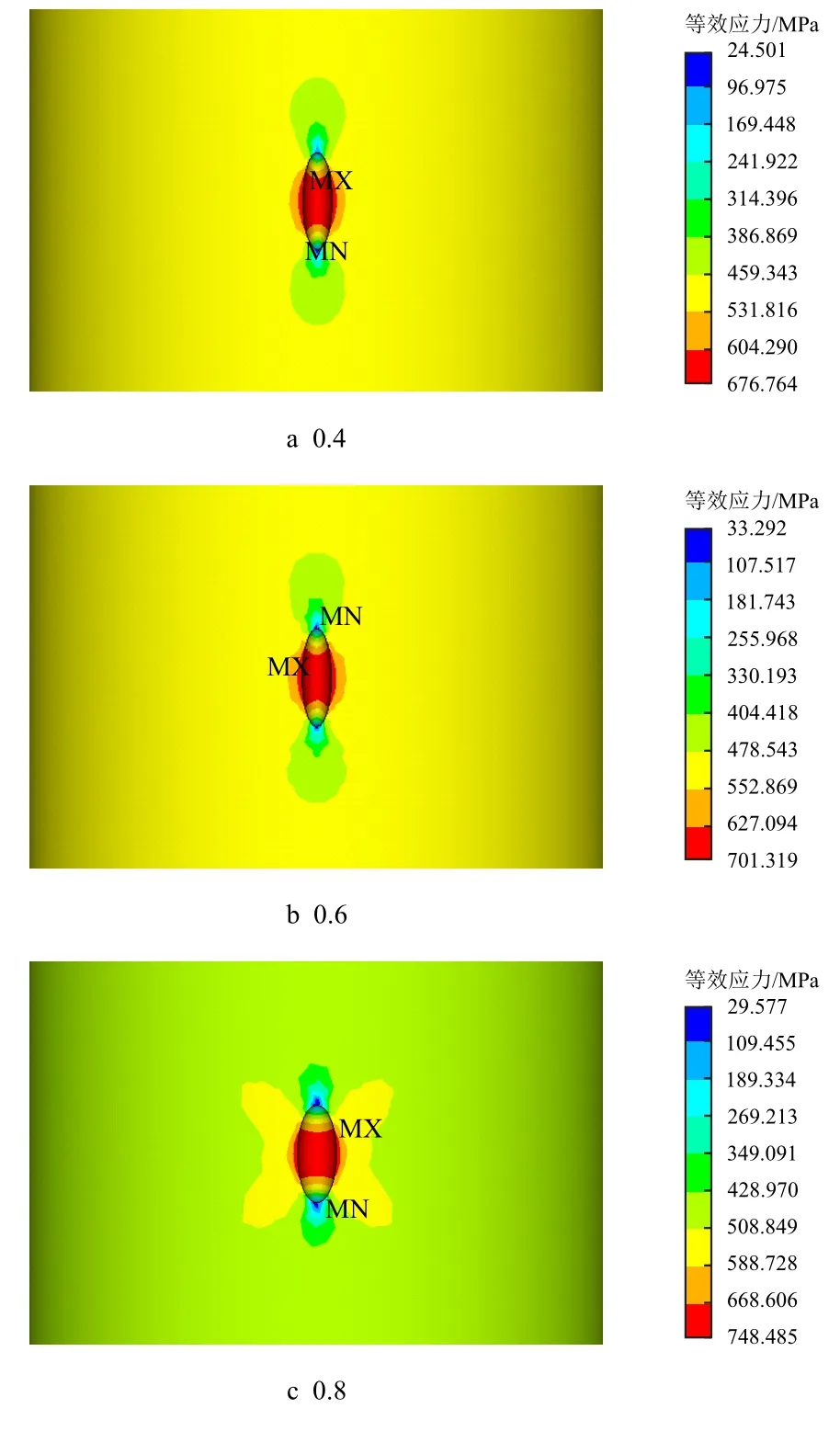
图6 不同宽深比下0.4 mm 深蚀坑的应力分布图Fig.6 Stress distribution of 0.4 mm deepth pit under different width-depth ratio

从图6 应力分布情况可以看出，高应力区仍然主要分布于蚀坑中心，相较于图4，最大及最小应力的分布位置规律一致，分别位于沿宽度和沿长度方向的蚀坑口处，但高应力区的分布规律有着明显区别。从应力分布变化情况可知，高应力区起初呈圆形分布于蚀坑中心处，随着蚀坑宽度的增加，高应力区分布区域出现了明显扩散，宽深比为0.8 时，高应力区以蚀坑为中心呈X 型扩散，这说明较大的蚀坑深宽比会加剧应力集中效应。

3 种深度蚀坑的应力集中系数与宽深比的关系如图7 所示。分析图7 可知，当蚀坑长度及深度不变时，应力集中系数随宽度的增加而增加，应力集中效应有所增强，这一现象有不利于带蚀坑或缺陷构件的后续服役。同时，根据图7 拟合出3 种坑深的工况下的公式，对比发现具有相同的变化趋势，进一步验证应力集中系数随宽度的变化规律。曲线呈现出应力集中系数随着宽深比的增加呈线性增加，线性拟合公式为

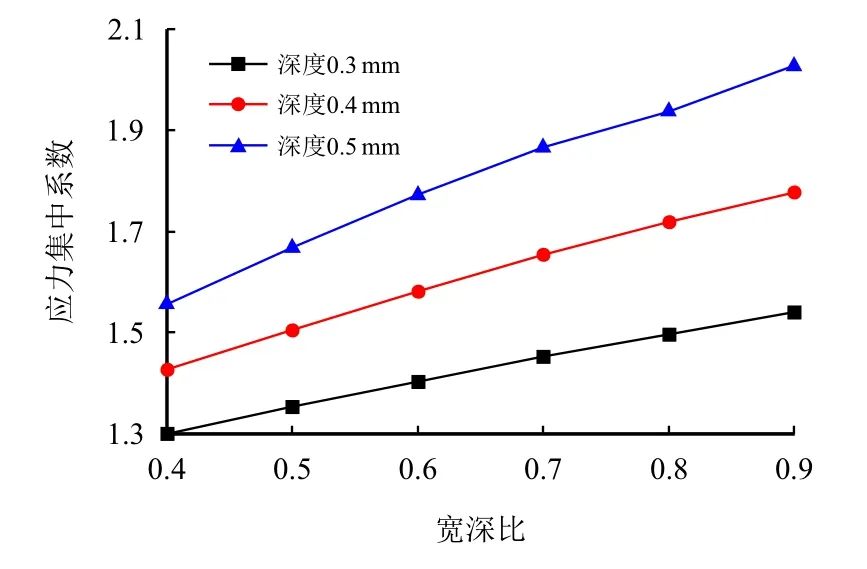
图7 应力集中系数随宽深比的变化规律Fig.7 Stress concentration coefficient varying with different width-depth ratio

3.3 深度变化对应力集中系数的影响

在研究深度的影响时，控制蚀坑的长宽不变，通过改变深宽比来探究蚀坑深度对应力集中系数的影响。根据设置3 种不同宽度的工况来验证变化规律的准确性。图8 是蚀坑宽度0.5 mm，深宽比取0.4、0.6 和0.8 时的应力云图。从图8 的应力分布情况可知，最大及最小应力的分布规律没有变化，仍然分别位于宽度方向蚀坑口和长度方向蚀坑口。从应力分布变化情况可知，随着深宽比的增加，高应力区扩散范围明显减小，这一现象加剧了应力集中效应，与宽度的影响类似，同样不利于带蚀坑或缺陷构件的后续服役。

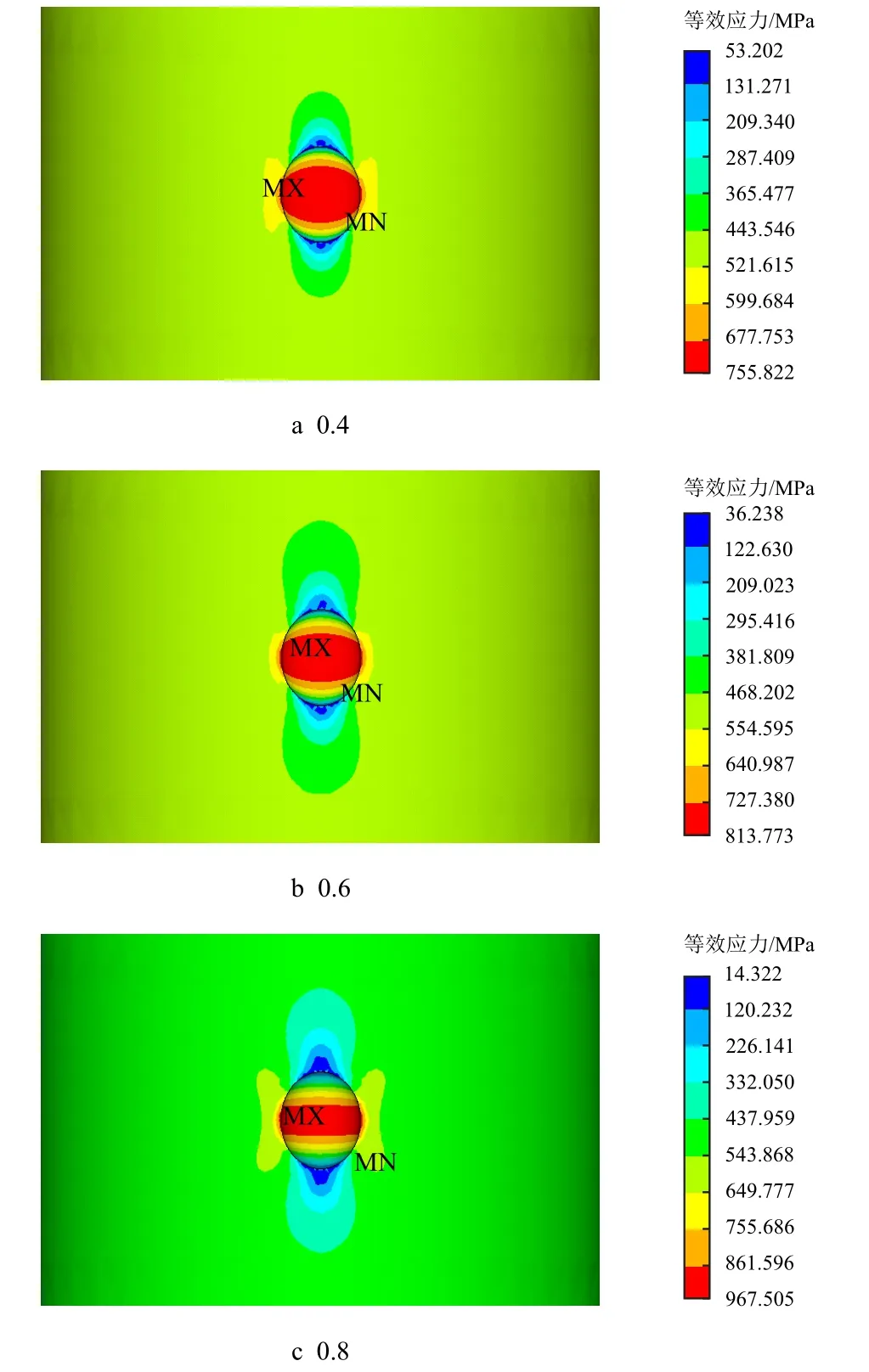
图8 不同深宽比下0.5 mm 宽蚀坑的应力分布图Fig.8 Stress distribution near the pit under different depth-width ratio(the width of pit is 0.5 mm）

3 种宽度（0.5，0.6,0.7 mm）蚀坑的应力集中系数与深宽比的关系如图9 所示。

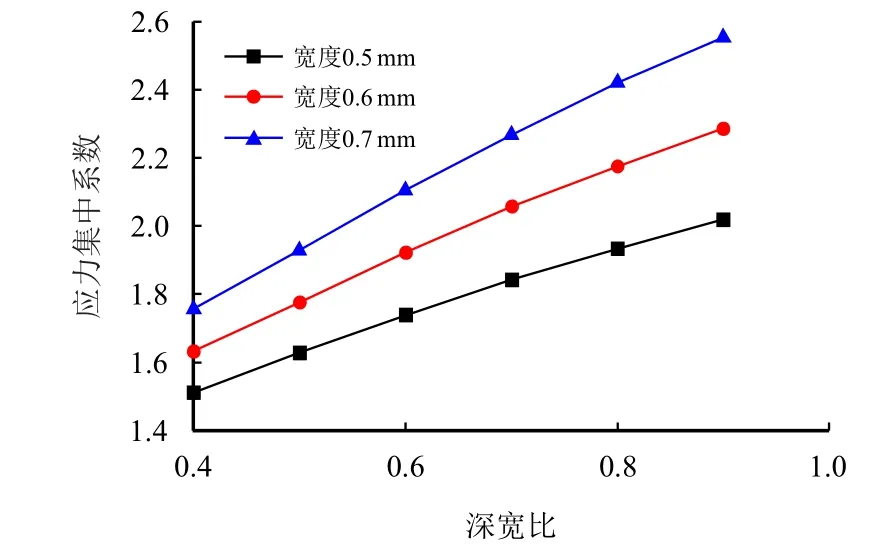
图9 应力集中系数随深宽比的变化规律Fig.9 Stress concentration coefficient varying with different depth-width ratio

通过分析图9 可得，当蚀坑长度及宽度不变时，应力集中系数随深度的增加而增加，应力集中效应有所增强。同时，根据图9 拟合出应力集中系数在3 种蚀坑宽度下的公式，见式（4），应力集中系数随着深宽比的增加呈线性增加。

3.4 长宽深对应力集中系数的影响程度比较分析

前述讨论了单个尺寸因素对应力集中系数的影响，本小结基于前面所得到的尺寸比与应力集中系数的拟合公式，量化讨论具有相同尺寸变化幅度的3 个尺寸对应力集中系数的影响程度，从而确定对蚀坑应力集中影响程度最大的因素，进一步明确最不利于构件受力的蚀坑形状。

当深度与宽度增加时都会导致应力集中效应加剧，从图7 及图9 中可知，随着宽深比和深宽比的增加，应力集中系数都是近似线性增加，由于深宽比的拟合公式具有更大斜率，说明相比于深度，宽度对应力影响因素的影响更大。而随着长宽比的增加，应力集中系数下降幅度较大，在长宽比趋于1的过程中变化幅度有所下降。采用二次函数对其进行拟合，发现长宽比从0.4 变化至0.9 的过程中，其斜率都远大于另外两个线性拟合公式的斜率，这说明在蚀坑的3 个尺寸因素中，应力集中系数对蚀坑长度最为敏感。

文献[10]对锈蚀钢丝在单轴荷载下的疲劳性能进行实验研究，实验结果见表3。

表3 由单轴拉伸试验得到的腐蚀钢丝的疲劳性能Tab.3 Fatigue results generated by testing corroded steel wires under uniaxial tension loading

研究表明，在相同荷载条件下，蚀坑的深度越大，钢丝的疲劳寿命越短，而蚀坑的长度越长，其疲劳寿命越长，这证明了深度大的蚀坑具有更大应力集中系数，而长度大的蚀坑具有更小的应力集中系数。

综合上述分析，从结构受力的角度来说，当半椭球形蚀坑的长度较短，深度和宽度较长时，蚀坑的应力集中系数会较高，此时是不利的蚀坑形状。

4 结论

（1）高强钢丝应力集中系数随蚀坑长度的增加而下降，随其宽度的增加而上升，随其深度增加而上升。

（2）根据蚀坑尺寸比与应力集中系数曲线所拟合得到的公式可知，蚀坑长度因素的改变对缓和应力集中现象影响最大，深度因素其次，宽度因素最小。长度的影响程度远超其他两个因素。

（3）通过量化对比3 种尺寸的拟合公式，得到最不利于锈蚀钢丝服役的蚀坑形状为：长度较短，宽度和深度较长的椭球形蚀坑。

符号说明

F轴面拉引力，MPa；

d深度，mm；

l长度，mm；

Kt应力集中系数，无因次；

σmax最大等效应力，MPa；

S名义应力，MPa。