氢原子渗透对管线钢微裂纹扩展的影响研究

徐涛龙 ，何恭震，张 毅，冯 伟，王 炜，3

1.西南石油大学石油与天然气工程学院，四川 成都 610500

2.国家石油天然气管网集团有限公司西气东输分公司，上海 浦东 200122

3.广州燃气集团有限公司，广东 广州 510627

引言

近年来，随着高钢级管道的大量敷设，管道本体安全正面临着越来越多地挑战。在管道输送过程中，内部介质的掺氢输送（存在未完全净化的硫化氢）和外部酸性环境中的氢原子都会对管道产生危害。研究表明[1-4]，管道中多起失效事故都由应力腐蚀开裂（Stress Corrosion Cracking，SCC）和氢损伤引起，氢原子在金属中会削弱其强度，而后加速应力腐蚀开裂的发生。由于晶体结构中存在着杂质原子、位错、裂纹、晶界和界面等，这都会对氢原子产生吸附作用，使金属结构发生脆化，从而导致灾难性损伤，这种现象也被称为氢脆（Hydrogen Embrittlement，HE）。针对高钢级管道的氢脆现象，学者们进行了大量研究[5-7]，但氢原子对晶间裂纹生长的微观机理仍有待进一步探索。

由于纳米金属实验的技术手段不足，将会对材料微观结构演化规律的观测产生影响。针对实验条件严苛、操作时间较长和测定难度较大等困难，采用分子动力学（Molecular Dynamics，MD）开展材料的微观分析已经成为目前最常见的研究方法之一。周国辉等[8]和李忠吉等[9]利用分子动力学方法分别研究氢原子对铝单晶和镍单晶的影响，都认为氢原子会促进裂纹扩展和位错发射。沈海军[10]采用分子动力学方法分别对铝单晶和双晶在含氢条件下进行拉伸模拟试验，结果表明氢原子的引入会降低铝材料的力学性能，材料破坏程度和氢原子的数量呈正相关性，且铝双晶对氢脆现象更为敏感。许天旱等[11]研究了双晶α-Fe 在不同界面旋转角度和不同氢原子浓度的力学性能变化，结果表明，双晶α-Fe 的峰值应力随着氢原子浓度的增加而减小。近几十年来，高钢级管线钢的典型组织一直都被认为是铁素体-渗碳体共析层状结构组成的珠光体组织[12]，且有学者[13]通过慢速率拉伸试验表明铁素体-珠光体钢对氢脆十分敏感，因此研究氢原子对铁素体-渗碳体层状结构的影响对高钢级管线钢抗脆化设计具有一定的指导意义。

本文运用分子动力学方法，首先建立Bagaryatskii 晶向的铁素体-渗碳体片层与终端界面结构，通过引入氢原子，来观测不同氢原子浓度下晶间裂纹扩展行为。然后对其不同受载阶段进行探讨，获取不同氢原子浓度下模型应力-应变曲线，研究其开裂的相关机制，最后对裂纹尖端开裂过程中模型发生的相变及位错进行分析。该研究可对由氢脆引起的高钢级管线钢的裂纹止裂技术与安全评定提供一定的理论指导。

1 模拟方法和过程

1.1 晶向关系

Howell[14]等通过透射电子显微镜（Transmission Electron Microscope，TEM）对珠光体的晶向关系（Orientation Relationships，ORs）进行研究，发现主要具有Bagaryatskii、Isaichev 和Pitsch-Petch3 种晶向关系[14-15]。

其中，Bagaryatskii 晶体朝向为[100]θ‖[110]α、[010]θ‖[111]α和(001)θ‖(112)α，Isaichev 晶体朝向为[010]θ‖[111]α和(103)θ‖(011)α，而Pitsch-Petch 晶体朝向为[010]θ2.6°‖[131]α和(001)θ‖(215)α。

目前，已有许多学者[16-17]对Bagaryatskii ORs的珠光体进行了大量理论分析，其中Guziewski[18]认为Bagaryatskii ORs 的晶体最有可能在珠光体中形成界面结构，Ruda[16]也使用Bagaryatskii ORs 建立了Fe-C 体系的EAM 势函数并进行相应计算。因此本文选取具有Bagaryatskii ORs 的珠光体展开铁素体-渗碳体界面裂纹扩展研究。

通过坐标变换将铁素体晶胞从a=[100]、b=[010] 和c=[001] 转 换 为a=[1-10]、b=[111] 和c=[11-2] 排列，运用ATOMSK 可将其进行变换，随后在笛卡尔坐标系下建立晶体模型。建立的原始铁素体单胞晶格常数为a=b=c=2.866 4×10-10m，重构后的铁素体单胞晶格常数为a=4.053 7×10-10m、b=2.482 7×10-10m，c=7.021 2×10-10m。

1.2 片层模型的建立

无论何种原子级别的界面，都需要考虑其微观自由度的影响，其中最为重要的便是界面中每个单元的终止面。

由于铁素体特有的BCC 晶格的高度对称性，其终止面结构和化学性质都是相同的。然而在渗碳体晶体中可能存在着8 种不同的终止面，如图1 所示。通过观察可以将渗碳体最外两层原子的终止面定义为：C-Fe1平面、Fe-Fe1平面、Fe-C1平面、C-C1平面、C-Fe2平面、Fe-Fe2平面、Fe-C2平面和C-C2平面。虽然渗碳体中原子相对于铁素体在1 平面和2 平面是不同的，但当铁素体和渗碳体结合后，将整个晶体模型进行翻转180°，可以发现1 平面和2 平面的能量和结构并没有明显的变化，所以可将终端界面简化为以下4 种：C-Fe、Fe-Fe、Fe-C 和C-C。以下建立模型的渗碳体界面终止面以C-Fe 类型为例。

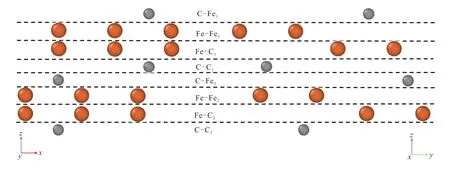
图1 渗碳体终端分类（红色为Fe 原子，灰色为C 原子）Fig.1 Terminal classification of cementite（red is Fe atom,gray is C atom）

首先，建立铁素体-渗碳体片层模型，其中，铁素体尺寸大小为18.242 nm×2.696 nm×6.319 nm，原子总数为26 730 个（图2 红色部分）。渗碳体尺寸大小为18.216 nm×2.731 nm×6.314 nm，原子总数为32 256 个（图2 蓝色部分）。

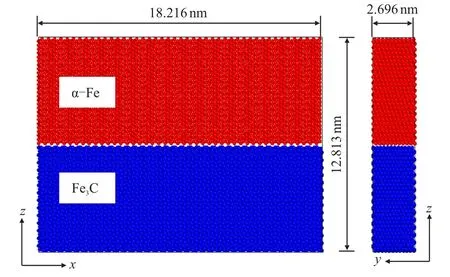
图2 铁素体-渗碳体初始模型（红色部分为铁素体，蓝色部分为渗碳体）Fig.2 Terminal classification of cementite（red part is ferrite,blue part is cementite）

然后，将两部分模型沿z方向合并，为保证晶体的稳定性和各个方向长度最大程度的重和，通过移动上半部分原子即铁素体部分来确定平面的相对位置，最后得到铁素体-渗碳体界面模型。

在不含氢原子的初始铁素体-渗碳体模型中，其模型尺寸为18.216 nm×2.696 nm×12.813 nm，原子总数为58 986 个。

在晶界中间预制一条穿透裂纹，长度为3 nm，根据氢浓度（原子数之比）的不同，将氢原子均匀地散布在铁素体-渗碳体模型当中，如图3 所示。

图3 含氢原子铁素体-渗碳体模型（红色为铁原子，蓝色为碳原子，黄色为氢原子）Fig.3 Ferrite-cementite model with hydrogen atom（red is iron atom,blue is carbon atom,yellow is hydrogen atom）

1.3 弛豫与加载

在分子动力学模拟的过程中，势函数是整个模拟过程的关键，势函数的选取决定着模拟结果的对错。由于Fe-H-C 之间的三体势函数尚未被完善开发，所以本文采取了3 个双体势函数来进行替换。在考虑Fe-C、C-C 和Fe-Fe 之间的相互作用时，虽然Meam[19]势函数精度更高，但其计算成本过大，因此，选取精度较强且计算成本偏低的Tersoff[20]势函数。同时，采用Ramasubramaniam 等提出的势函数来描述Fe-H 和H-H 之间的相互作用，该势函数已被大量应用于由氢原子引起的金属铁相变、位错等方面的力学行为研究[21-22]。C-H 则选取LAMMPS 中自带的Airebo 势函数。

在弛豫过程中，沿x、y、z的3 个方向施加周期性边界条件，大大降低了边界效应的影响。保持温度为300 K 恒定，对模型进行共轭梯度法（Conjugate Gradient，CG）进行能量最小化，压力为0 的NPT 恒温恒压弛豫30 ps。弛豫后效果图如图3 所示，除预制的3 nm 穿透裂纹外，其余部分某些铁素体原子和渗碳体原子甚至已结成同一晶粒。为证明本次弛豫的准确性，分别对弛豫前后铁素体和渗碳体中的Fe 的径向分布函数（Radial Distribution Function，RDF）进行计算，计算结果如图4 所示。可以看出两者最大峰值均有大幅度下降，弛豫后Fe 的RDF 曲线在峰值过后仍降为零，这说明晶体继续保持着有序性。在载荷过程中，分别固定模型上下4 层原子，对充分弛豫后的样本沿z轴进行单轴拉伸应变加载，加载应变率为5×108s-1，时间步长为1 fs。

图4 弛豫前后铁素体和渗碳体RDF 对比Fig.4 RDF comparison of ferrite and cementite before and after relaxation

2 模拟结果及分析

2.1 应力-应变曲线

为研究不同氢浓度对铁素体-渗碳体力学性能的影响，图5 得出了单轴拉伸时不同氢浓度下（0、1.1%、2.2% 和3.2%）铁素体-渗碳体的应力-应变曲线，表1 为轴向拉伸过程中峰值应力值和峰值应力处应变。选取的氢浓度范围参照Kuopanportti[23]的实验方法，这是由于氢原子在实际扩散中较为缓慢，所以选取的氢浓度值略高于现场实验。

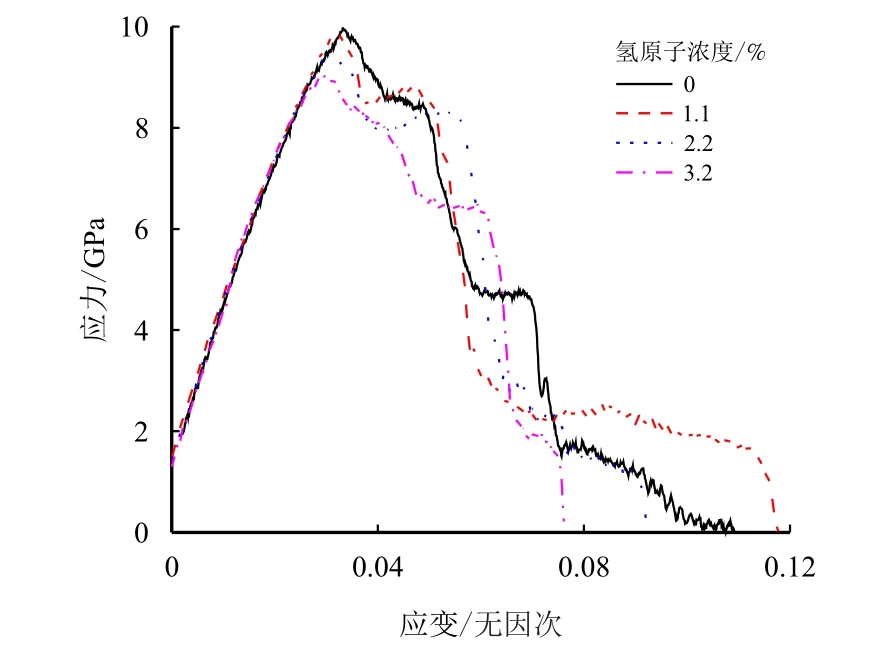
图5 不同氢浓度下铁素体-渗碳体应力-应变曲线Fig.5 Stress-strain curves of ferrite-cementite under different hydrogen concentrations

可以看出，虽然氢原子浓度不同，但随着应变的增加，4 种模型在初始阶段都会经历近乎重合的弹性拉伸过程，这与Moro 等[24]的研究工作相吻合，说明含氢模型和无氢模型在弹性应变过程中不会存在本质性的差异。

随后应力将到达一个峰值，通过表1 可以看出，随着氢原子浓度的增加，峰值应力随之减小，且氢原子浓度越大应力下降趋势越明显。当氢原子被引入金属结构材料中时，一些铁原子在未施加任何载荷之前会偏离晶格位置并导致晶格畸变。这种晶格畸变使孪晶更容易形核[24]，这是峰值应力随氢原子浓度增加而下降的重要原因之一。

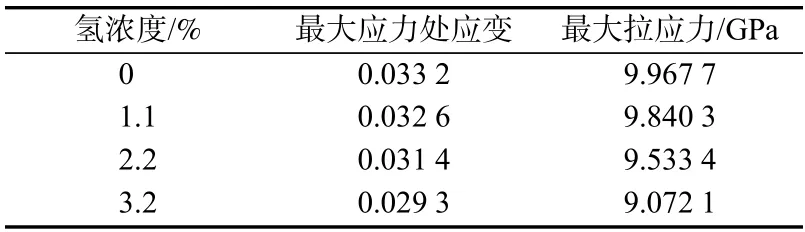
表1 轴向拉伸过程中力学参数Tab.1 Mechanical parameters during axial tension

当各个模型分别达到临界应变时，由于原子间的化学键断裂，裂纹将发生快速扩展，并进入塑性阶段；在经历第一个短暂的应力急剧下降过程后，模型将进入一个屈服过程，即所谓的平台期，不同的模型在平台期的应力范围也有变化；度过此次平台期后，模型将进入第二次应力急剧下降过程，随后将进入新的平台期。

在此平台期，氢原子浓度为0 时，应力保持在4.7～5.0 GPa，氢原子浓度为1.1 % 时，应力保持在2.0～2.5 GPa，氢原子浓度为2.2% 时，应力保持在2 GPa 左右，氢原子浓度为3.2% 时，应力保持在1.5～2.0 GPa 之间。可以看出，氢原子浓度越高，在此平台期平均应力值越小。随后模型应力将再一次进入下降过程，直至应力减小为0，材料彻底失效。

2.2 裂纹尖端开裂过程

为进一步了解铁素体-渗碳体界面裂纹扩展这一动态过程，以氢原子浓度为2.2 % 的铁素体-渗碳体晶体模型为例，通过进一步观察可以发现，裂纹扩展过程中会出现裂纹尖端原子堆积，裂纹尖端后缘空位形成，孔洞生长和孔洞连接等现象，如图6所示。

图6 氢原子浓度为2.2%时铁素体-渗碳体晶体模型裂纹开裂过程中原子堆积、空位形成、孔洞生长及连接现象（红色为铁原子，蓝色为碳原子，黄色为氢原子）Fig.6 Phenomenon of atom accumulation,vacancy formation,hole growth and connection during H atom density is 2.2%model crack crackin（red is iron atom,blue is carbon atom and yellow is hydrogen atom）

随着加载的进行，裂纹尖端开口逐渐扩大，裂纹尖端处原子将会重新进行排列，偏离理想晶格位置而后在裂纹尖端处出现堆积，如图6a 所示，当应变为2.03 时，裂纹尖端两侧出现原子堆积现象，与无氢模型相比较，由于氢原子的引入，晶体原子的有序性发生破坏，更容易发生位错形核，原子排列的混乱导致裂纹尖端塑性形变的产生；图6b 为应变为5.49 时的瞬时模型，由于塑性应变的不断增加，裂纹尖端处少部分原子间相互作用变小，从而导致孔隙出现于原子当中，如图6c 所示，当应变为6.14时，随着孔隙的进一步增大，将会形成原子空位；随着加载的进一步增加，原子间空位将会越来越多，随后将会联结而形成孔洞；图6d 为应变为6.93 的模型，随着新生成的小孔洞不断生长，而后将会与发生孔洞连接现象。

随着孔洞的不断形成和连接，上面界面将会逐渐分离而后产生新的裂纹尖端，随后将不断重复原子堆积、空位形成和孔洞生长及连接等过程，使裂纹不断地向两侧扩展。

随着应变的加载，界面以初始裂纹尖端为起点，分别向x轴方向左右两侧扩展。可以发现，4 个模型的开裂顺序总是左侧裂纹先于右侧裂纹。一般情况下，晶体的晶向决定着晶界裂纹的扩展方向，裂纹朝着一侧呈脆性断裂[25]。因此，左右两侧裂纹尖端位错形核将会不对称，裂纹的开裂过程自然也不相同。

2.3 相变与位错分析

为研究模型在裂纹开裂过程中的变形机制，运用Ovito 中位错分析法（Dislocation Analysis，DA）与公共近邻法（Common Neighbor Analysis，CNA）对模型的位错及相变进行分析。

通过本次研究观察发现，在弹性开裂的阶段，模型中不会出现位错；当模型进入塑性开裂的过程中，将会出现大量1/6＜112＞（Shockley）位错与1/3＜001＞（Hirth）位错。

Hirth 位错和Shockley 位错都只发生在FCC 结构的相变区域中，且位错绝大部分发生于铁素体片层中（图7）。

图7 铁素体-渗碳体在不同氢原子浓度下处于相同应变时原子结构图（蓝色原子为BCC 结构，绿色原子为FCC 结构，红色原子为HCP 结构，黄色线段是Hirth 位错线，绿色线段是Shockley 位错线）Fig.7 Atomic structure diagram of ferrite-cementite at the same strain under different hydrogen atom concentrations（blue atoms have BCC structure,green atoms have FCC structure,red atoms have HCP structure,yellow segments are Hirth dislocation lines,and green segments are Shockley dislocation lines）

随着氢原子的增多，将会促进Shockley 位错形核，随即长大、滑移、相互反应，促使Shockley 位错增长。并且，可以看出而Shockley 位错长度增长较为快速，而Hirth 位错的长度增长则较为缓慢。

从图7 中也可发现，大量的相变与位错都集中在裂纹的右侧上方区域，即阻碍右侧裂纹的萌生与扩展。

通过观察得知，在模型开裂进入塑性应变期时，BCC 相首先向FCC 相和HCP 相转变，随着BCC 晶格数量到达一个低谷，而后FCC 相和HCP 相开始向BCC 相进行转变，整个过程BCC 晶格的数量关系呈现出一个开口向下的抛物线，BCC 晶格数量先递减，随后再递增。

不仅如此，我们发现氢原子的浓度也会对相变的关系产生影响，从图7 可知，当模型同处于应变为5.16 时，氢原子浓度为0 的模型中的BCC 晶格数量大大超过2.2%浓度模型。

如图8 所示，氢原子浓度和FCC 相向BCC 相和HCP 相转变时临界应变呈现线性关系，可以看出，随着氢原子浓度的增加，相变的临界应变也在逐步升高，这也说明氢原子会阻碍FCC 相与HCP相向BCC 相转变，即塑性断裂作用下降，脆性断裂作用增强。

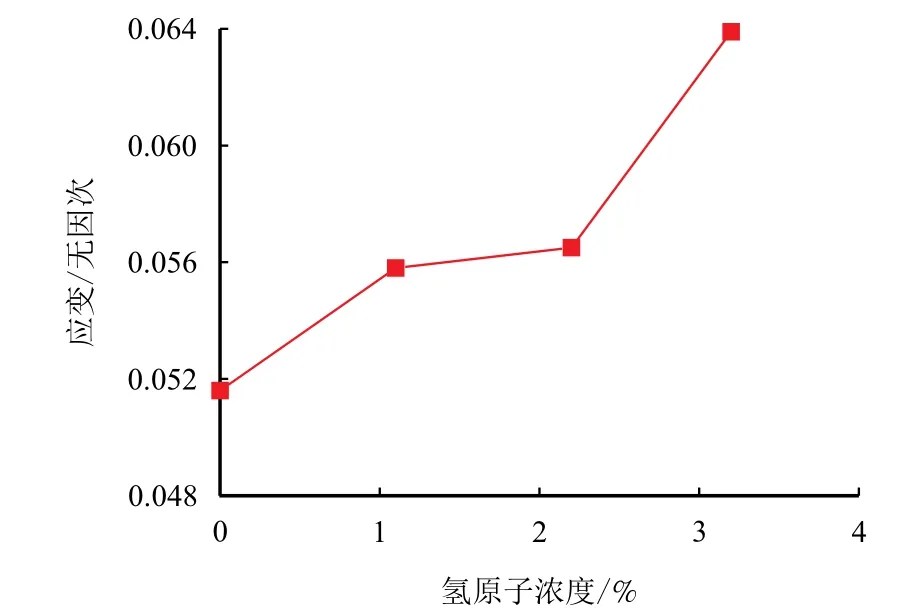
图8 氢原子浓度随FCC 相和HCP 相向BCC 相转变时临界应变的函数关系曲线Fig.8 Function curve of hydrogen atom concentration with critical strain during FCC phase transition to BCC phase

3 结论

（1）铁素体-渗碳体在裂纹开裂过程中峰值应力随着氢浓度的增加而减小，且氢浓度越大，减小的趋势就越明显。氢原子的增加仅仅会对开裂速度产生影响，而不会改变裂纹的开裂顺序。

（2）在裂纹扩展的过程中，会出现裂纹尖端原子堆积、空位形成、孔洞生长和连接等现象。裂纹尖端扩展过程中，氢原子并不会对裂纹开裂方向产生影响，裂纹的左侧总是先于右侧开裂。

（3）模型开裂进入塑性应变时，大量位错及相变集中在裂纹右侧，从而阻止右侧裂纹开裂，且氢原子会阻碍FCC 相和HCP 相向BCC 相转变。