一种棋类计算机博弈强化学习智能体的决策依据解释方法

刘 贺，张小川，刁志东，王 森

(重庆理工大学 两江人工智能学院，重庆 401135)

基于深度学习算法的人工智能产品已经开始落地应用，在取得较好成果的同时，也发生了很多意外事故。比如，微软基于深度学习开发的聊天机器人Tay，在实践中说出了涉及种族歧视的言论，特斯拉设计的自动驾驶汽车发生撞人事件，因此，近几年来深度学习模型的可解释性问题逐渐成为了一个较为关注的领域[1-2]。深度学习的可解释性研究对于这一类算法和基于这类算法的产品落地应用来说具有重要的意义[3-4]。

深度学习加强化学习构成的深度强化学习算法，已经在智能体博弈领域有了非常成功的实践，尤其是在棋类博弈当中[5-6]。在深度学习给博弈智能体带来成功的同时，也把其可解释性差的问题引入进来。因此，对于深度强化学习智能体模型的可解释性[7]研究也是必不可少的。对于该类算法，由于其内部参数结构非常复杂，所以目前很多研究者将其看作为一个“黑盒”[8]，从其输入、输出进行解释性研究，并在此基础上设计了很多方法来解释这个“黑盒”的判断逻辑或者判断依据[9]。已有学者开始尝试使用注意力机制[10]或者引入公理化的决策理论[11]等方法从模型内部进行模型的可解释性研究。

在从模型内部进行可解释性研究的同时，不少学者提出用显著图[12]这种有较好展示效果的方法从外部对模型的决策进行可解释性研究。Iyer等[13]提出使用显著图来解释该类游戏智能体决策依据(如图1所示)，以国际象棋智能体为目标，针对深度强化学习算法，设计了一种方法，计算棋局上每个特征的决策显著性，最终生成显著图，展示了每个特征对于智能体决策的重要性，即解释了智能体的决策依据。Greydanus等[14]设计了一种基于扰动的显著图解释方法，解释了一些基于深度强化学习的像素游戏智能体的决策依据，该方法通过删除或者加入高斯噪声的方式，改动输入图像的像素特征，通过查看智能体是否改变决策的行为，以此来判断该像素对智能体决策的重要性，并对重要性程度进行量化，最终通过显著图的方式展示出来，如图2所示。Puri等[15]提出了对于深度强化学习智能体的决策依据，需要从“重要性”和“相关性”2个角度对其进行解释性输出。即在判断一个特征重要性的同时，要考虑该特征与要解释的动作是否相关，若该动作与要解释的动作不相关，则其在决策中的重要性将非常小，只有该特征与要解释的动作相关时，才会关注该特征的重要性，并将其输出在显著图上。在此思路的基础上，Puri等[15]设计了SARFA解释方法，并用多个游戏智能体验证了其有效性。

图1 文献[13]的方法效果图

图2 文献[4]的方法效果图

综上所述，基于显著图的解释方法已经在Atari游戏上验证了其有效性。但在棋类游戏智能体的决策依据解释当中，只会对有棋子的特征点进行决策显著性评估。从博弈行为角度分析，棋盘的所有合法落子点对于智能体的决策也具有参考价值，比如围棋这一项目，智能体不仅需要对棋盘上双方的落子分布进行分析，棋盘上如果有大片未落子的空白区域，那么此区域对于“气”的争夺也是很有意义的，如果在空白区域的中心位置或者其他重要位置落子，则会抢先占领该区域，为自己后续的棋子布局做好铺垫。同样，在国际象棋中，也需要对所有未落子的空白区域进行分析，比如双方棋子都可以到达的位置就可能需要进行抢占式的落子，达到限制对手的目的。因此，上述方法在解释棋类智能体决策依据时，仍然不够全面。针对该问题，提出一种基于显著图的解释方法，不仅评估棋局已有棋子点特征对决策的显著性影响，而且还设计了一种方法针对棋盘上空白的落子点，评估其在决策当中的显著性，最终综合两者，得到较为全面的棋局特征的显著图，以期更全面地解释棋类智能体的决策依据。实验结果表明，本文的方法初步达到了全面解释棋类智能体决策依据的目的。

1 相关工作

对于基于深度强化学习的棋类智能体的决策依据，往往从其算法原理上进行解释，针对基于深度强化学习的棋类智能体M，通常是使用深度神经网络来拟合Q值函数，从Q值函数值当中使用某种策略(比如e-greedy策略)，选择最终的行动策略。

根据已有规定，定义棋类智能体M的状态空间为S，对应的动作空间为A，对局期间，每一步棋盘状态为s(s∈S)，对应的Q值为Q(s)，智能体对于状态s做出最终决策，即选择动作a(a∈A)。棋局上所有特征集(棋子和空白落子点)为F，每一处特征点为特征f。

目前大部分用于解释智能体决策依据的解释方法都是基于扰动生成显著图方法，对于当前状态s中的特征f，扰动特征f，将状态s更改为exps,比如在围棋游戏中，通过移除棋子的方式来达到该目的，在像素游戏中会通过加入高斯噪声的方式达到该目的。在状态改变之后，让智能体对修改后的状态进行判断得到Q(exps,a),∀a∈As∩Aexp s。通过Q(s,a)和Q(exps,a)的差值计算得出该特征f的显著性S[f]。

根据文献[15]，对于特征的显著性分析可以从定性的相关性和定量的重要性两方面评估特征f，首先要判断f是否与a相关，当f与a相关性较低时，f的重要性应该很低，当f与a相关性较高时，则对f在决策中的重要性进行计算，此外，相关性、重要性2个指标的内涵定义如下：

1)相关性：对于当前状态s中的特征f,f∈F，如果特征f被改变之后对决策动作a之外的其他动作产生同样的影响，即其他动作expa(expa∈A),expa≠a的预期回报也发生了变化，则说明特征f与决策动作a的决策相关性较低

2)重要性：在特征f与决策动作a决策相关性较强的前提下，在特征f被改变之后，棋局对应状态由s变为exps，决策动作a的预期回报由Q(s,a)变为Q(expx,a)，计算|Q(s,a)-Q(exps,a)|，差值为特征f在决策中的重要性程度。

2 基于显著图的棋类智能体决策解释方法

基于前人的研究，根据文献[15]提出的SARFA解释性方法，对其进行改进，设计出一种可以更全面地解释棋类智能体决策的解释性方法。该方法不仅能够计算棋局上落子点的特征显著性，而且从博弈行为方面分析棋局空白点特征的显著性，最终将棋盘全局特征的特征显著性以显著图的方式展示给外界，以此解释棋类智能体对于棋局状态的决策依据。下面分别从已落子区域、空白区域进行特征分析。

2.1 已落子区的特征显著性分析

在此，从决策相关性和决策重要性两方面对已落子区特征进行显著性分析。

2.1.1相关性分析

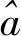
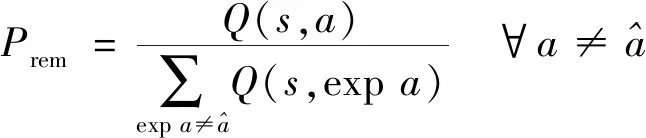
(1)

使用相对熵来衡量原始状态s与修改特征f后，状态exps对应动作预期回报的差异程度。

DKL=Prem(exps,a)||Prem(s,a)

(2)

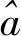
2.1.2重要性分析

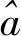
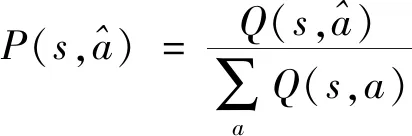
(3)

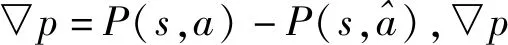
2.1.3显著性分析

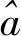
DKL的值与特征f的相关性成反比，因此，将DKL值映射至0～1区间，再取倒数的方式，使其最终映射值与特征f的相关性成正比。

(4)

最终计算特征f的显著性

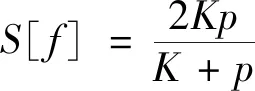
(5)

2.2 空白区域的特征显著性分析

从博弈行为而言，下棋者不仅会注意棋盘的棋局状态，同时还会根据空白区域，一是分析棋型布局，二是分析对方落子的威胁程度，最终做出落子决策，因此，可以对空白区域特征进行显著性分析。

对于空白区域，从人类经验角度而言，更加注重的是对手在不同位置落子后对本方局势的影响程度，对于基于深度强化学习算法的智能体而言，这种影响可以从对应的Q值中各个动作的估值改变程度中反映出。因此对于空白区域特征的显著性分析可以从落子前后Q值的改变程度进行分析，即模拟对手在空白区域的不同位置落子，观测落子前Q(s,a)和落子后Q(exps,a)的变化差异，并对这种差异进行量化，最终可以得到各个落子点特征在决策中的显著性。

空白区域主要注重其对于智能体后序决策的影响程度，所以不需要像落子区域一样从相关性和重要性2个方面进行分析，仅仅分析其对于智能体决策中的依据(Q值)的影响程度即可。

使用KL散度对落子前后Q值的变化程度进行计算，KL散度定义公式：

(6)

KL散度用来计算P(x)与Q(x)的相似度，二者相似度性越高，则KL散度越小，恰好可以定量的表示落子前Q(s,a)和落子后Q(exps,a)的变化差异程度。

对于空白区域特征f，使用添加棋子的方法，模拟对手角色在空白区域落子，改变特征f，使棋局状态由s变为exps，根据其对智能体的所有合法动作a(a∈AS)的预期回报的影响程度来判断该特征对于智能体决策的显著性S[f]，使用相对熵来计算状态改变前后动作a预期回报的变化程度，进而表示特征f的显著性。

S[f]=Q(s,a)||Q(exps,a)

(7)

对手的落子会从两方面影响己方的决策，一是对于己方某个动作的估值产生很大影响，二是对于己方整体的大部分动作的估值产生影响，此处计算出的特征显著性S[f]包含了两方面的差异程度，因此，可以定量反映落子点特征在决策中的显著性。

2.3 输出最终显著图

为提高可视化程度，最终生成的显著图具体包含有落子区域和空白区域所有特征的显著性。按此前的相关性和重要性两方面相关显著性，分析出空白区域特征的显著性。二者的量纲不同，所以使用归一化处理，将二者映射到统一量纲下，最终对二者进行合并，生成最终的棋局特征显著图，以此展示整个棋盘全局特征在智能体决策中的显著性，进而达到解释智能体决策依据的目的。

1)落子区域特征显著性S[f]d归一化处理：

(8)

2)空白区域特征显著性S[f]b归一化处理：

(9)

最终将S[f]d和S[f]b合并至同一棋盘中，并以图像的形式进行输出。

3 实验设计

3.1 实验方法

使用基于深度强化学习的围棋智能体和国际象棋智能体进行实现，给其棋盘局势，让智能体执子进行下一步落子的决策，在做出决策的同时使用本文的解释方法对智能体的决策进行解释性输出，进而分析智能体的决策依据，并与前人的方法进行对比，验证本文方法的有效性。

3.2 实验内容

对于上述两类智能体，以棋谱的形式输入给智能体，智能体执子落子后，使用本文方法计算棋局上各个特征在智能体决策中的重要性，并使用图形化的方式进行输出，得到最终的显著图，并对其进行分析。

3.3 实验结果

3.3.1针对围棋智能体的实验以及结果分析

最终对围棋智能体的决策依据解释效果如图3所示。图3(a)为棋盘状态，智能体执黑子，下一步决策动作为在A16落黑子；图3(b)为SARFA方法解释的智能体决策依据，仅仅计算了落子区域特征显著性；图3(c)为最终生成的棋盘全局特征显著图。

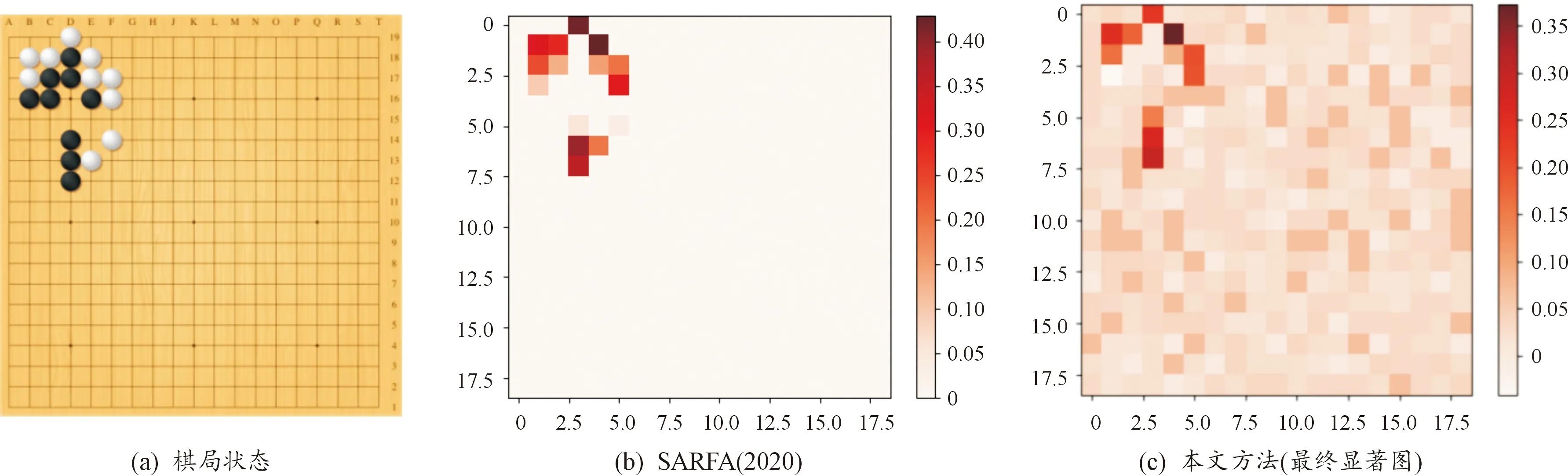
图3 围棋智能体决策显著图

可以看出，在落子区域的特征显著性分析上，本文方法计算的特征显著性与SARFA方法计算的基本一致，对于整个棋局形式，白方E18处的棋子最为重要，白方可以凭借E18的棋子向右扩充自己“气”的范围，但是黑方在此处没有棋子分布，若单独落子容易被白方吃掉，因此智能体考虑了对自己最有利的白方棋子，即B18、C18、B17处的棋子，是白方在左上的中心棋子，智能体在A16落子有利于进一步吃掉白方在左上区域的棋子。

在空白区域，智能体同样认为有一部分的落子点较为重要，左下和右下部分目前双方都未落子，因此在这些区域的中心点落子可以抢先占据布局，如M列第3、7、8行都可以做抢占式的落子，而边角处的落子点对于“气”的争夺作用不大，因此智能体认为其重要性较低。

3.3.2针对国际象棋智能体的实验以及结果分析

最终针对国际象棋智能体的决策依据解释效果如图4所示。图4(a)为棋盘状态，智能体执白方，将“兵”行至b4位置；图4(b)为SARFA方法解释的智能体决策依据，仅仅计算了落子区域特征显著性；图4(c)为最终生成的棋盘全局特征显著图。

图4 国际象棋智能体决策显著图

对于棋盘上所有的棋子，智能体认为对方“王后”对于本方的威胁最大，其与本方的“王”最近，且是棋盘上棋力最强的棋种。本方靠近“王”的棋子同样重要，用于吃掉对面的“王后”或者卡位限制对方王后的走位。

对于空白区域，智能体主要关注与本方“王”主要能走位的区域，同时关注于对方“王后”能走位的落子位，若对方“王后”越过棋盘第4行，则将对本方“王”产生很大威胁，但是“王后”不能越子行棋，因此将本方的“兵”行至b4，一方面可以阻止对方“王后”直接越过第4行，同时，对方“王后”若吃掉该子，则本方的“马”可以吃掉对方的“王后”，这样的行棋可以很好地限制住对方“王后”的走位。

4 结论

针对智能体的决策依据有所不同的情况，提出了适合棋类智能体的解释方法，从棋局落子区域与空白区域2个区域对智能体的决策依据进行解释，较好地展示了棋类智能体的决策依据。

该方法对于围棋、不围棋等吃子棋类智能体的决策依据解释效果较好，但是对于中国象棋、国际象棋等吃子棋特征种类较多的棋类智能体，解释效果仍然有不足，因此下一步研究将尝试设计一种通用型更强的解释方法。