Artin A-左遗传环的若干研究

田 岩，焦 旸

(辽宁师范大学 数学学院，辽宁 大连 116029)

0 引言

环论是代数学的一个重要分支，其理论和方法在数学的许多领域都有广泛的应用，而模论和同调代数是研究环的主要方法.同调代数作为研究环的工具，用模来刻画环的结构是环论的一种发展趋势.

遗传环理论是环论和模论的重要组成部分.众所周知，左遗传环是一类重要的环.近年来，很多专家和学者关注左遗传环的研究，取得了丰硕的成果.1992年，郭宇[1]引入并刻画了左相对遗传环，讨论了左相对遗传环与左遗传环和左半遗传环的关系.证明了左相对遗传环的左理想的自同态环是左半遗传的；左相对遗传环上的有限生成相对投射模的自同态环是左半遗传环.1999年，李晓红[2]在遗传扭论(T，F)中给出并刻画了T-遗传环与F-遗传环.2003年，朱占敏[3]推广了遗传环，引入左亚遗传环的概念，研究了左亚遗传环的性质，并给出其等价刻画.2006年，孙平[4]对遗传环进行了推广，定义了包含范围更广的环类——NoetherN-左遗传环，给出了NoetherN-左遗传环的等价命题，并利用NoetherN-左遗传环对左凝聚环和N-半单环进行了刻画.进而，给出了模对Noether环的刻画.2009年，班秀和[5]研究左遗传环和左亚遗传环的性质，给出几个等价条件，讨论了左亚遗传环的直和以及它与SI-环和半单环的关系.2010年，周震[6]通过对短正合列、相对投射模和相对内射模等的研究，给出了左遗传环的等价条件，从而刻画了左遗传环.更多关于遗传环的结果见文献[7-10].

2011年，文献[11]从模的角度研究半单环，将模论和同调代数中的两个主要研究对象——投射模和内射模进行了推广，引入了A-投射模，A-内射模的概念，由此构造出一种环，称为ArtinA-半单环.本文中的环R都是有单位元的结合环，模均指酉模.

1 A-左遗传环

为了得到更广的一类左遗传环，下面将左遗传环进行推广.利用A-内射模和A-投射模，引入A-左遗传环、A-左半遗传环和A-左凝聚环的概念，并给出A-左遗传环的等价刻画.

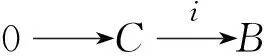
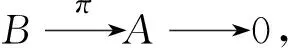
定义3若环R的每个左理想是A-投射模，则称R是A-左遗传环.

显然左遗传环是A-左遗传环，A-半单环是A-左遗传环.

定义4若环R的每个有限生成左理想是A-投射模，则称R是A-左半遗传环.

显然，A-左遗传环是A-左半遗传环.

定义5若Artin环R的每个有限生成左理想是有限表现的，则称R是A-左凝聚环.

定理2.1设R是Artin环，则以下命题等价：

(1)R是A-左遗传环；

(2)Artin模与A-内射模的商模是A-内射模；

(3)Artin模与A-投射模的子模是A-投射模；

(4)对R的每个左理想I，都有正合列

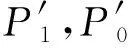
证明(1)⟹(2)设E是Artin模，A-内射模，E′是E的商模，R是Artin环，I是R的左理想.根据图1，由已知，I是A-投射模，那么存在β：I→E，使得α=πβ，又因为E是A-内射模，那么存在β′：R→E，使得β=β′i，因此α=πβ=πβ′i，πβ′：R→E′，由文献[11]中命题2，可得E′是A-内射模.

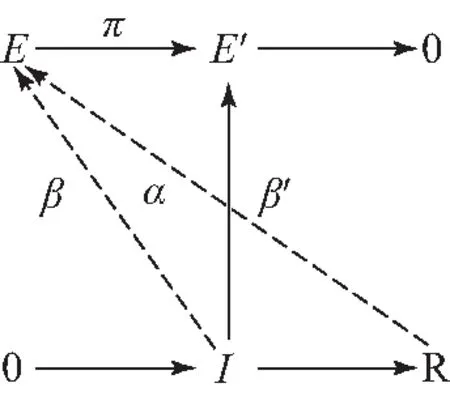
图1 A-投射模的正合列交换图Fig.1 Commutative diagram of the exact sequence of A-projective module

(2)⟹(3)设P是ArtinA-投射模，P′是P的任意子模.根据图2，其中行皆正合，E是ArtinA-内射模，由已知E′是A-内射模，根据A-内射模的定义，存在β：P→E′，使得α=βl.又因为P是A-投射模，由A-投射模的定义可知，存在γ：P→E，使得β=πγ.因此，α=βl=πrl，其中γl：P′→E.因为E是Artin模，根据A-投射模的定义，可知P′是A-投射模.

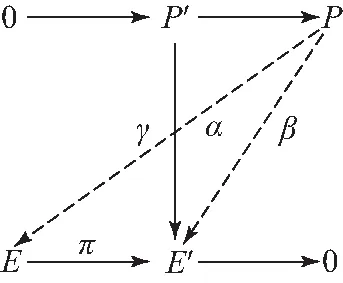
图2 A-内射模的正合列交换图Fig.2 Commutative diagram of the exact sequence of A-injective module

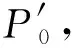
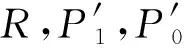
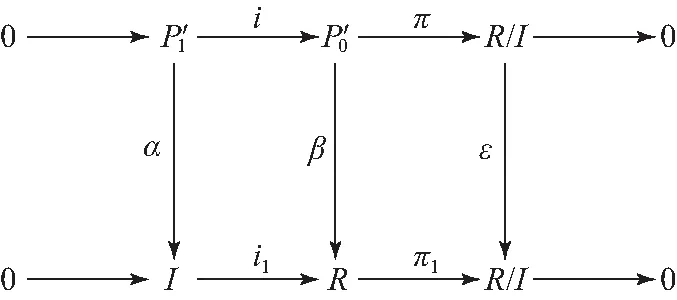
图3 正合列交换图Fig.3 Commutative diagram of exact sequene

π1(x)=π1βi(a)=επi(a)=0，

可得x∈kerπ1=Imi1，即Imβ⊆Imi1.由文献[12]在中定理3.5可知，存在模同态映射α，使得i1α=βi.

再根据文献[13]中定理3.62的证明可知，存在短正合列

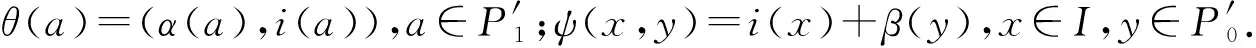
由文献[11]中命题5可得，I是A-投射模，这说明R是A-左遗传环.

2 A-左遗传环与A-左凝聚环的关系

前面已经给出A-左遗传环和A-左凝聚环的概念，下面讨论二者的关系.从而，体现模对Artin环的刻画.

定理2设R是Artin环，则以下命题等价：

(1)每个Artin模都是A-内射模；

(2)每个Artin模都是A-投射模.

证明(1)⟹(2)设M是Artin模.如图4，B是Artin模，由已知C是A-内射模，所以底行可裂.因此，一定存在β，使得α=πβ，即M是A-投射模.

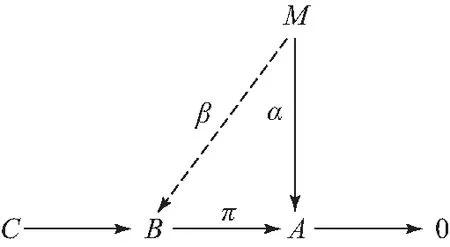
图4 A-内射模交换图Fig.4 Commutative diagram of A-injective module

(2)⟹(1)设M是任意Artin模，如图5，其中B是Artin模，从而B/C也是Artin模.由已知B/C是A-投射模，所以底行可裂，hi=I，αhi=α.令αh=β，则βi=α，即M是A-内射模.

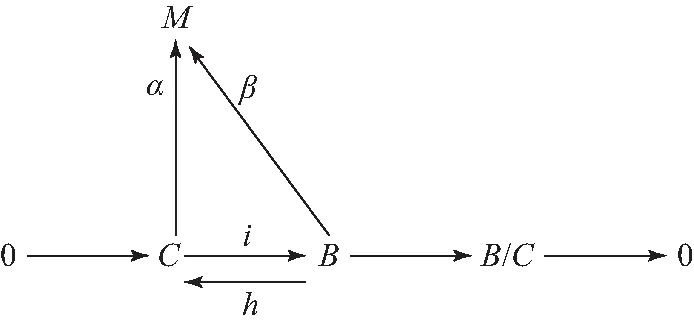
图5 A-投射模的交换图Fig.5 Commutative diagram of A-injective module

命题2.1ArtinA-左半遗传环是A-左凝聚环.

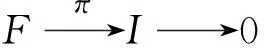
定理2.3对Artin环R，R是A-左遗传环的充分必要条件是对任一个Artin左R-模，其任意两个A-内射R-子模的和仍是A-内射R-模.

证明(⟹)设M是任意一个左R-模，N1，N2是它的任意两个A-内射R-子模，由文献[11]中命题3，可知N1⨁N2是A-内射模.存在满同态

φ：N1⨁N2→N1+N2→0，

其中(n1，n2)→n1+n2.故

N1+N2≅N1⨁N2/kerφ.

因为R是A-左遗传环，根据定理2.1可得：N1⨁N2/kerφ是A-内射模，故N1+N2是A-内射模.

(⟸)令

W=E⨁E，

V={(x，x)∈W|x∈K}，

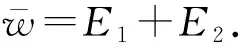
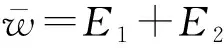
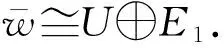
若e+k=e′+K∈E/K，则e-e′∈K，那么

(e-e′，e-e′)∈V，

即

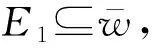
可得

即

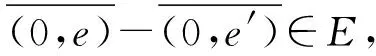
从而

φ(e+K)=φ(e′+K)，

故φ为映射.对任意e+K∈kerφ，则有

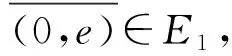
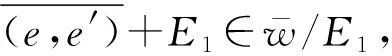
即存在e′+K∈E/K，使得

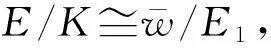
3 结语

本文首先利用A-内射模和A-投射模将左遗传环进行推广，定义了更广的一类环——A-左遗传环.进而，引入A-左半遗传环和A-左凝聚环.然后，研究A-左遗传环的性质，给出等价刻画.最后，讨论A-左遗传环、A-左半遗传环以及A-左凝聚环的关系.进而从模的角度刻画Artin 环.本文的研究方法体现了模对环的刻画，具有一定的借鉴意义.