基于电磁感应法测量亥姆霍兹线圈磁场的改进

徐林超，向文丽

(楚雄师范学院 物理与电子科学学院，云南 楚雄 675000)

亥姆霍兹线圈是一对彼此平行且联通的共轴圆形线圈，结构简单并能产生一定可调、均匀性较好的磁场，适合做大尺寸均匀磁场发生器，除此之外，亥姆霍兹线圈还广泛应用于生产、技术、物理等领域.

亥姆霍兹线圈磁场的测量是大学物理实验必做的项目之一，其测量方法主要有“霍耳效应法”[1]和“电磁感应法”[2]两种.何冰心等[1]利用霍耳效应法测量亥姆霍兹线圈空间磁场，得到空间磁场的大小、形状及范围；王倩等[2]通过电磁感应法测量磁场的实验方法测量载流圆线圈轴线上的磁场，并很好地验证了由毕奥-萨伐尔定律求解得到的载流圆线圈轴线上的磁感应强度公式；杨能勋等[3]用传统方法，即用亥姆霍兹线圈磁场测定仪进一步探究了亥姆霍兹线圈空间磁场均匀区域的大小、形状和范围；武成艳等[4]利用Origin软件对亥姆霍兹线圈磁场测量实验进行数据处理和图形拟合分析，得出亥姆霍兹线圈中心轴线上的磁场分布.当前，大多数研究报道为亥姆霍兹线圈磁场的理论推导、传统方法测量和软件模拟等，而利用RLC电路的物理特性改进电磁感应法测量亥姆霍兹线圈磁场的报道甚少.本文在电磁感应法测量亥姆霍兹线圈磁场分布的基础上，基于RLC电路的物理特性，利用电容与亥姆霍兹线圈串联设计了电路谐振的改进实验,以提高实验效率和精确度.

1 实验原理

1.1 亥姆霍兹线圈磁场分布

亥姆霍兹线圈由一对完全相同的共轴圆形导体线圈组成，两组线圈之间的距离等于圆线圈的半径r. 当在亥姆霍兹线圈上通有同向电流I时，运用毕奥-萨伐尔定律得出在亥姆霍兹线圈轴线上的磁感应强度[5]为

(1)

从式(1)可知，当X的值在一定小范围内变化时，磁感应强度B的变化微小，则可以认为在亥姆霍兹线圈中心轴线上一定小范围内存在均匀分布的磁场.

基于电磁感应法测量磁感应强度[2]的公式为

(2)

其中，N为探测线圈的匝数，Um是探测线圈感应电动势最大值，S为探测线圈的横截面积.

1.2 RLC串联谐振

RLC串联电路是一种由电阻(R)、电感(L)、电容(C)组成的串联电路结构，当回路中接入一个输出电压幅度一定、输出频率f持续可调的正弦交流信号源时，电路的许多参数都将随着信号频率的变化而变化.

当容抗等于感抗时，容抗与感抗互相抵消，即

(3)

此时，电路总阻抗为最小值，回路电流达到最大值，整个电路呈阻性，这个现象即为RLC串联电路谐振，谐振频率为

(4)

f0称为RLC电路的固有谐振频率，它跟电路的参数密切相关，与信号源没有关系.

基于此，一般可以通过2种办法令RLC串联电路实现谐振，第1种方法为：保证LC不变改变ω；第2种方法为：保证电源频率不变，改变L或者C.实验中一般常改变C达到串联谐振.

1.3 传统电磁感应法结合RLC串联谐振改进实验

由RLC串联谐振电路的物理特性可知，在RLC串联谐振电路中，感抗和容抗相互抵消，电路为纯电阻电路，电流达到最大值.传统电磁感应法测量亥姆霍兹线圈磁场，亥姆霍兹线圈自身电感对亥姆霍兹线圈的磁场测量具有一定影响，存在测量值整体偏小、读数不方便的问题.因此，本实验在电磁感应法的基础上，通过与亥姆霍兹线圈串联电容达到谐振改进实验，从而使亥姆霍兹线圈自身电感感抗和串联电容容抗相互抵消，消除亥姆霍兹线圈自身电感感抗对实验的影响，以解决传统电磁感应法测量亥姆霍兹线圈磁场存在的问题，力求实验操作方便、效果明显，并提高实验的精确度.

基于此，设计实验如图1所示，令电容C和亥姆霍兹线圈串联，当开关闭合时，函数信号发生器[6]输出正弦交流电信号，通过优化选择电容C的大小和亥姆霍兹线圈发生谐振，使亥姆霍兹线圈两端的电压达到最大值.

为了形象地判断谐振现象并精确测量亥姆霍兹线圈磁场分布，实验中，将晶体管毫伏表接入亥姆霍兹线圈两端，选择电容C的大小后通过晶体管毫伏表读数，当其测量值达到最大值时可判断该电路达到谐振；在电路达到谐振时，将探测线圈水平放至亥姆霍兹线圈中心轴线上，移动探测线圈至探测点，将示波器[7]接入探测线圈两端，旋转探测线圈，利用示波器可形象地观察探测线圈旋转时其感应电动势的变化；并在示波器上由其波形读出该探测点的感应电动势的最大值，由式(2)得出该探测点的磁感应强度.

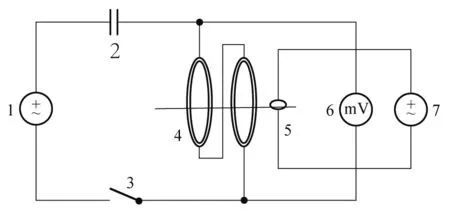
1. 函数信号发生器; 2. 电容; 3. 开关; 4. 亥姆霍兹线圈; 5. 探测线圈; 6. 晶体管毫伏表; 7. 示波器图1 改进方法实验原理图

2 基于电磁感应的改进方法测量亥姆霍兹线圈磁场

本实验采用的亥姆霍兹线圈为恒利达公司出厂，其总匝数为1 000匝，内阻为70.8 Ω，电感值为190.0 mH，测得探测线圈横截面积为3.6×10-4m2，匝数500匝，亥姆霍兹线圈磁场测定仪的固有频率为1 000 Hz.亥姆霍兹线圈上通入3 mA的同向电流时，由亥姆霍兹线圈中心轴线上的磁场式(1)可得在中心轴线上的磁感应强度理论值，记录于表1.

通过几何作图的方法，初步确定亥姆霍兹线圈中心轴线的中心点，将探测线圈放至中心点位置的一定小范围内沿水平方向移动，同时旋转探测线圈找到最大感应电动势对应的位置，确定亥姆霍兹线圈磁场的中心点，将该点记为X/m的零点位置.

根据图1接好线路，实物图如图2所示，基于亥姆霍兹线圈测定仪固有频率为1 000 Hz，选择不同的串联电容C，分别为0.099×10-6F、0.100×10-6F、0.110×10-6F时测出不同电容参数下亥姆霍兹线圈中心轴线上不同探测点X/m的最大感应电动势，由式(2)计算出对应点的磁感应强度大小并记录于表1；为了比较亥姆霍兹线圈串联电容C改进方法测量磁场的优势，在其他参数相同的条件下，亥姆霍兹线圈不串联电容，测出了亥姆霍兹线圈的磁场分布数据记录于表1.

图2 改进法测量亥姆霍兹线圈场正视图

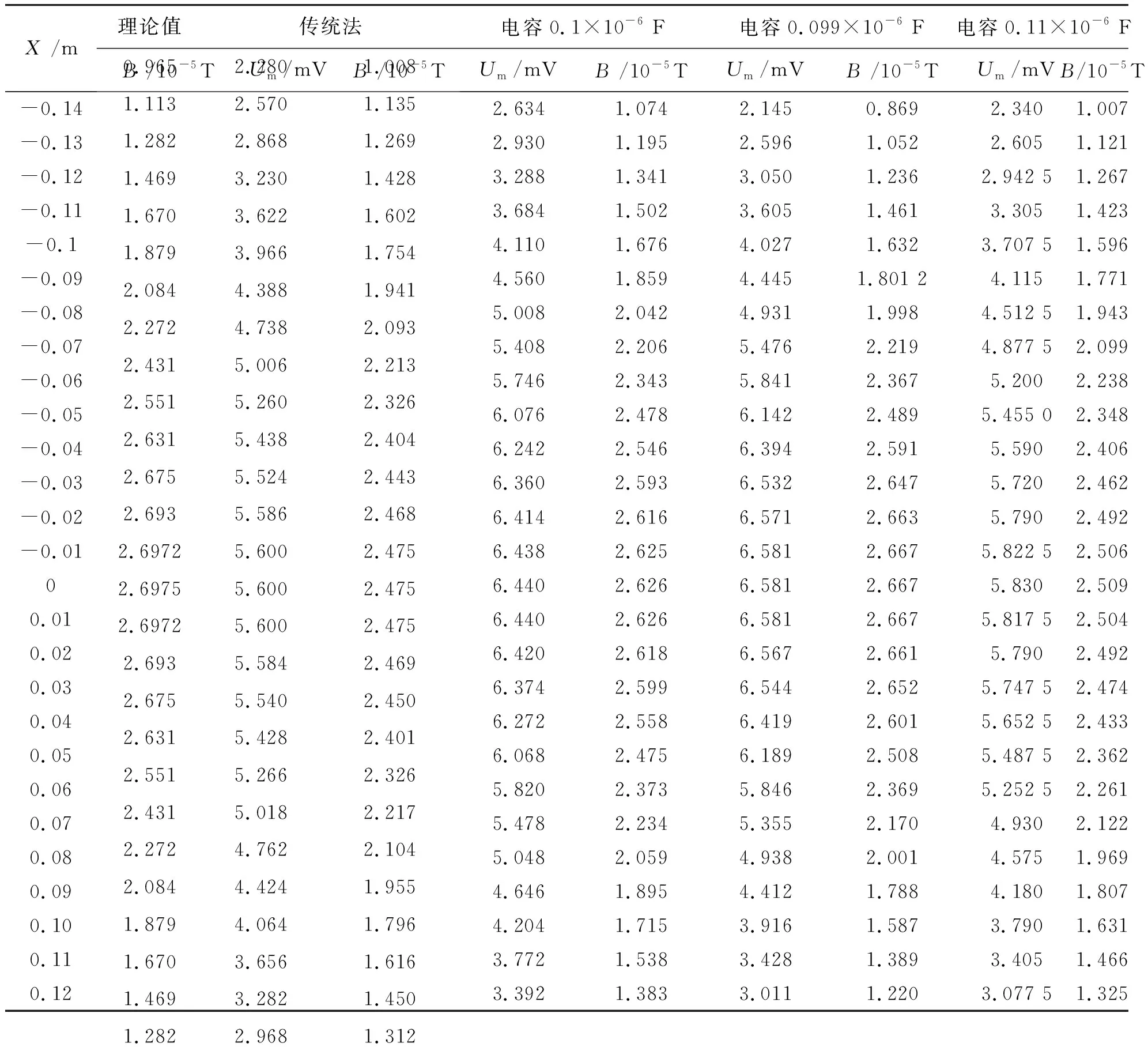
表1 亥姆霍兹线圈场理论值、传统法和改进法的数据记录

3 实验结果分析

近年来，用Origin 软件研究物理现象和规律具有良好的效果，本实验以亥姆霍兹线圈的中心轴线为坐标X轴，磁感应强度为坐标Y轴，利用Origin 软件作出亥姆霍兹线圈磁场分布图，如图3所示.

由图3可知，基于传统电磁感应法测量亥姆霍兹线圈磁场，即电路中亥姆霍兹线圈无串联电容时，其磁场分布图像远远低于理论计算下的磁场分布图，测量磁场值整体偏小；当电路中亥姆霍兹线圈串联电容时，测得的磁场分布图像较前者(无串联电容)整体上移，串联电容为0.11×10-6F时，所测得的磁场分布图像稍高于无电容串联时对应的磁场分布图像；即电容为0.1×10-6F时其图像较高，而电容为0.099×10-6F时，其图像处于三者中的最高处，该图像与理论计算下的磁场分布图像基本吻合；从该图中可知亥姆霍兹线圈中心位置(x=0)的磁场强度为2.667×10-5T，最接近于理论计算下的最大磁场值2.697 5×10-5T，误差为1.13%，而利用传统电磁感应法测量该点的磁场强度为2.475×10-5T，误差为8.25%.

综上，亥姆霍兹线圈与电容串联达到谐振测量其磁场改进方法在一定程度上可以消除亥姆霍兹线圈自身感抗的影响，相比于传统电磁感应法测量亥姆霍兹线圈磁场效果明显，更接近于理想状态下的亥姆霍兹线圈磁场分布.改进方法测量的磁场精确度均一定程度上大于传统电磁感应法的测量结果，在电容为0.11×10-6F时，测得的亥姆霍兹线圈磁场精确度稍高，而电容为0.099×10-6F时，测得的亥姆霍兹线圈磁场精确度最高，电容为0.1×10-6F时，所测得的亥姆霍兹线圈磁场精确度基于其他两者之间，则串联电容为0.099×10-6F时是3种参数中电容的最佳选择.

为了科学地量化测出亥姆霍兹线圈中心轴线各点的磁场分布关系，利用Origin拟合了最佳电容为0.099×10-6F时的亥姆霍兹线圈中心轴线位置和磁场的关系，其关系式为B=-71.08X3-104.67X2+0.44X+2.71，单位为10-5T，其拟合相关系数为0.99，与理论状态下的式(1)基本吻合，拟合不确定度为0.02×10-5T.

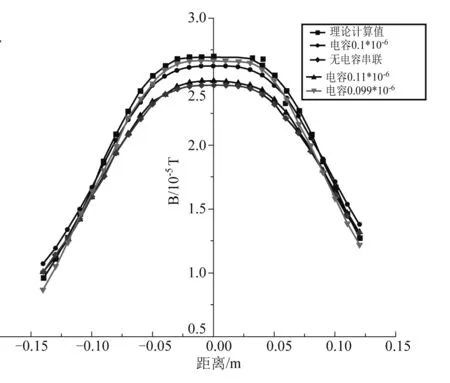
图3 亥姆霍兹线圈中心轴线磁场分布图

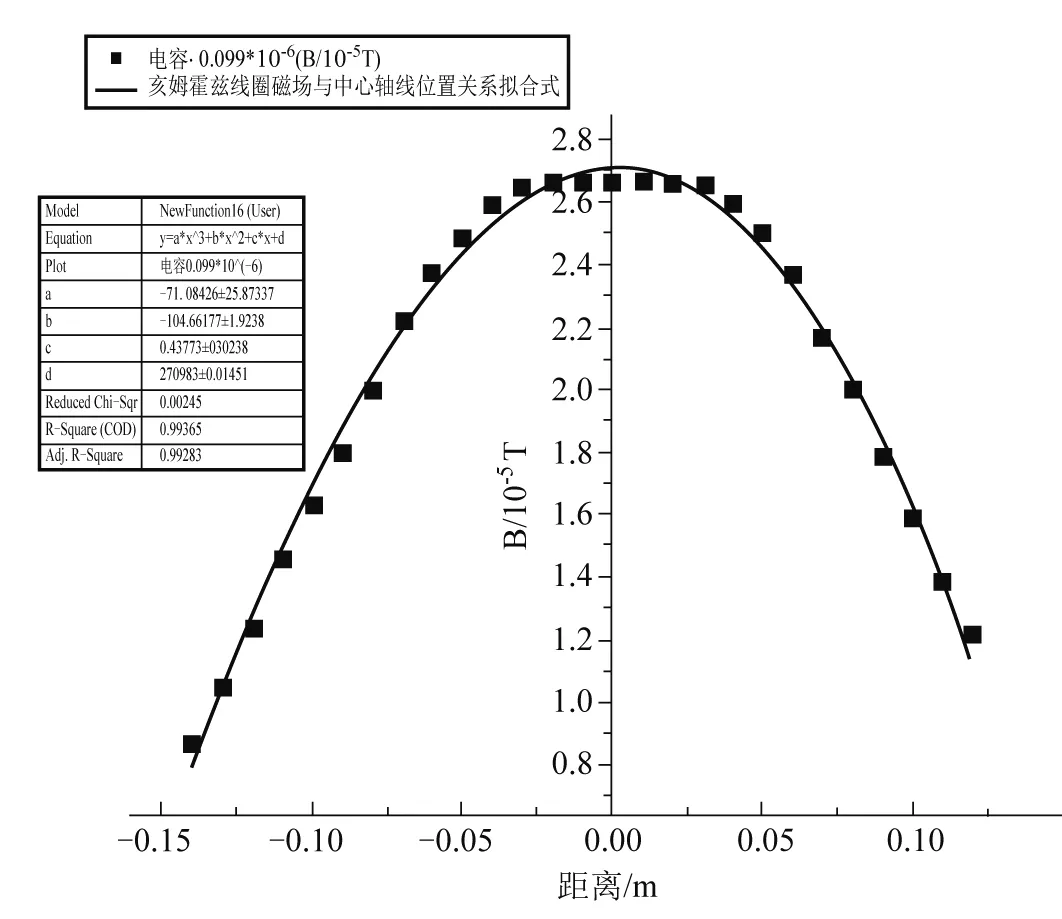
图4 改进方法(C=0.099×10-6F)测得的磁场分布拟合图

4 结论

本文在电磁感应法的基础上通过亥姆霍兹线圈串联电容达到谐振的改进方法，探究了不同串联电容参数下测得的亥姆霍兹线圈磁场分布，利用Origin软件作图并拟合分析了其亥姆霍兹线圈磁场与中心轴线位置的关系式，结论如下：

1) 改进方法一定程度上可以消除亥姆霍兹线圈自身感抗的影响，测得的亥姆霍兹线圈磁场精确度在一定程度上均大于传统电磁感应法的测量结果.

2) 串联电容C的大小不同程度上影响测量磁场的精度.3种选择电容中，在电容为0.11×10-6F时，测得的亥姆霍兹线圈磁场精确度稍高，电容为0.1×10-6F时，所测得的亥姆霍兹线圈磁场精确度基于其他两者之间，而电容为0.099×10-6F时，测得的亥姆霍兹线圈磁场精确度最高，是3种参数中电容的最佳选择.

3) 利用Origin软件拟合了最佳电容与亥姆霍兹线圈串联时的亥姆霍兹线圈中心轴线位置与磁场的关系, 拟合关系式与理论状态下的式(1)基本吻合.

4) 结合RLC电路的特点对传统的电磁感应法进行改进，实验效果明显，精确度高，科学可行.该方法为一种值得推广的测量亥姆霍兹线圈磁场的改进方法.