粒度对煤炭浮选动力学的影响浅析

郜大刚

(山西西山煤电股份有限公司 镇城底矿选煤厂，山西 太原 030200)

煤炭是世界上使用最广泛的化石能源，约占全球一次能源的30%和全球发电量的41%，尽管存在环境问题，但因其储量丰富，易回收，成本较低使得2050年之前煤炭在能源供应中仍扮演重要角色。世界上已探明的煤炭储量超过1.14万亿t，按目前的消费速度计算，足以满足153年以上的全球能源需求[1,2]. 原煤必须使用不同的技术进行加工，才能在粒度、灰分、硫分和水分含量方面达到所需的产品质量。要生产出经济价值最高的优质煤，必须综合运用多种选煤技术。所采用的选煤技术取决于煤的理化性质，如煤种(固有灰分和硫含量)和粒度，其中浮选技术是分选较细粒煤颗粒的有效方法[3].

煤炭浮选是一个非常复杂的过程，学者已经开发了许多模型来描述浮选过程。浮选动力学模型是最常用的浮选模型，它将颗粒、矿浆和流体力学性质有关的不同工艺参数与浮选速率常数联系起来。粒度对浮选速度有重要影响，是浮选过程中最重要的参数之一[4]. 本文综述了浮选动力学模型的发展历史，总结了粒度对浮选回收率、浮选速率常数和产品质量的影响。

1 粒度对浮选动力学的影响

粒度在浮选过程中影响气泡矿化、气泡尺寸分布、气含率、气泡-颗粒粘附的稳定性以及药剂吸附等。不同粒度的颗粒对浮选性能的表现不同，但都直接影响浮选回收率和浮选速率常数[5].

1.1 浮选速率常数

Gaudin等人从1931年对粒度与浮选回收率之间的关系进行研究，发现在相同的化学条件下，不同粒度的颗粒表现出不同的浮选动力现象。铜矿的最大浮选回收率在20～100 μm，磷矿的最大浮选回收率在60～200 μm，煤炭浮选的最佳粒度一般小于1.0 mm. Trahar的研究表明，细颗粒和粗颗粒的浮选回收遵循不同的规律，粗颗粒的回收对表面疏水性的变化比细颗粒更敏感。因此，粒度对浮选的影响引起了众多学者的关注并展开了广泛的研究[6]. Morris首先研究了粒度与浮选速率常数的关系，发现中等粒度能获得最大浮选速率，并且对于细颗粒和粗颗粒来说，浮选速率常数是递减的。与其他粒度相比，细颗粒的浮选速率常数较低，这主要是因为随着粒度的减小，颗粒与气泡碰撞的可能性降低。粒度对浮选速率影响的示意图见图1[7]，图中标记了对颗粒回收有不利影响的3种现象，即聚集(A)、夹带(E)和脱离(D)[8].

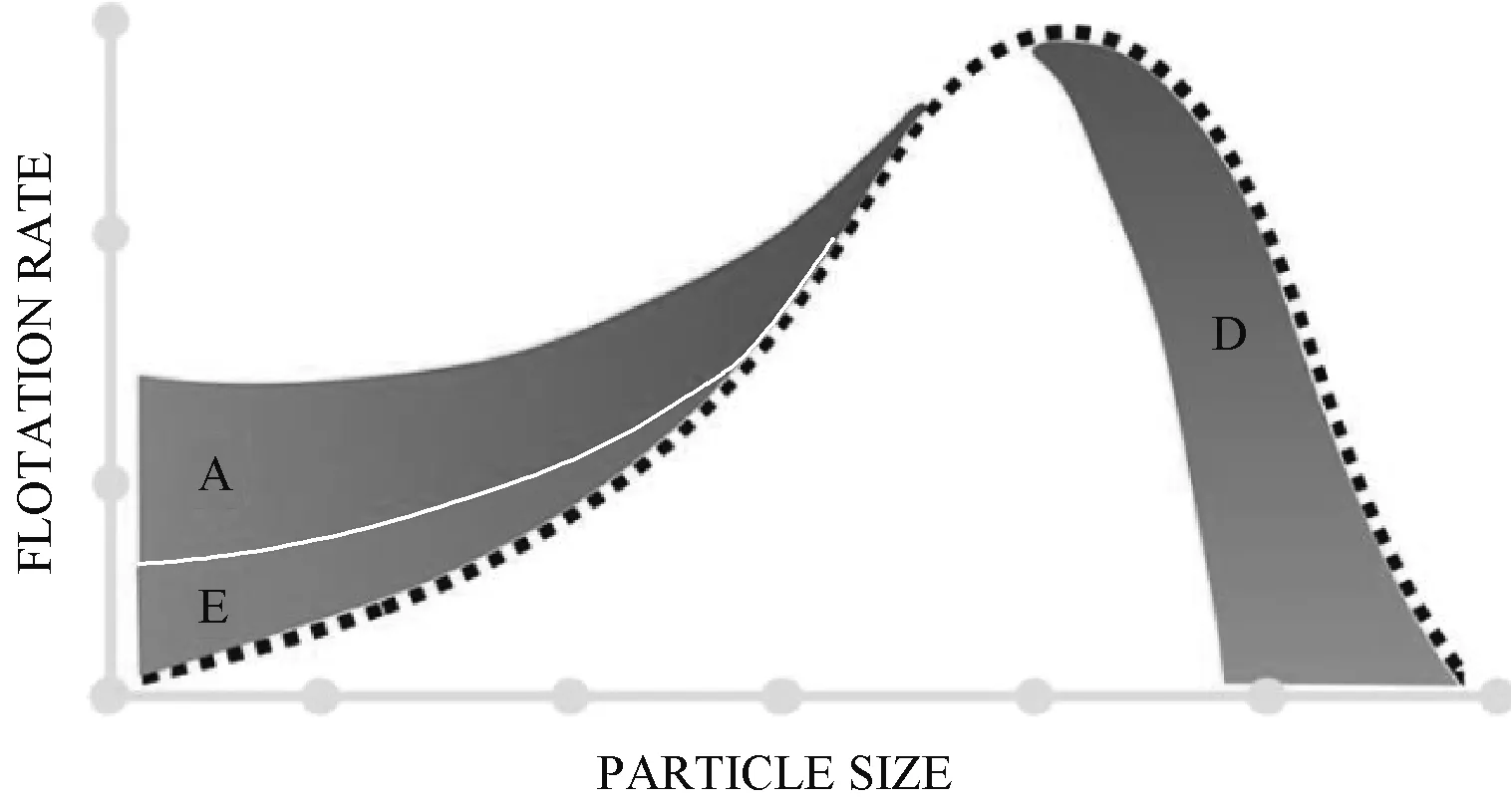
图1 粒度对浮选速率的影响图

Trahar将浮选速率常数定义为粒度的函数：

(1)

其中，A是比例系数，n是取值在1和2之间的参数[9].

颗粒大小和浮选速率之间的关系十分复杂，Al Taweel等人最先尝试定义碰撞概率和浮选速率常数之间的关系。对于疏水性很强的煤，他们发现浮选速率由碰撞概率(Pc)决定，碰撞概率随颗粒尺寸增加而增加[10]. Chander和Polat认为，造成这种结果的关键是细粒度颗粒在浮选过程中发生聚集[11,12]. 不同粒级浮选速率常数的差异也可以用浮选过程中碰撞和附着/脱附的综合作用来解释。细颗粒浮选速率低的主要原因是气泡-颗粒碰撞的概率低，而粗颗粒浮选速率低的主要原因是这些颗粒从气泡表面脱离的可能性高。

Mohns提出了浮选动力学速率随粒度变化的二次多项式模型[13]：

(2)

其中，a，b，c分别是由矿浆和药剂浓度共同决定的系数。

1.2 浮选回收率

Panopoulos等人研究了粒度分布对两种南非煤浮选的影响。根据浮选回收率与粒度的关系，发现最大回收率峰值出现在100～200 μm，在200 μm以上，浮选回收率迅速下降，当粒度为1.0 mm时，浮选回收率几乎为零。对于相对密度在1.3～1.7的10个粒度，浮选速率的差别很小，灰分含量为2%～31%. 可浮组分的最大浮选速率常数在-500～425 μm. 另外，对于较粗的颗粒，回收率随颗粒密度的不同而显著不同，对于细粒度，高密度的颗粒被有效地抑制[14-15].

Vanangamudi和Rao(1986)发展了间歇浮选模型，该模型表明，随着粒度的增大，浮选速率常数减小。建立了预测浮选产品可燃体回收率和灰分随药剂用量变化的数学方程。然而，该模型没有考虑入料粒度分布的影响。随后，又建立了一个独立参数定义的简单的间歇浮选动力学模型。该模型已经在不同的进料特性、药剂用量和操作条件下进行了测试。在间歇式浮选槽中进行了4种不同煤种的浮选试验。结果表明，任何粒度组分的浮选速率常数均与粒度组分的平均值、各粒度范围内灰分和非灰分的比例以及进料中-75 μm组分的比例有关。对于任何煤，入料中无灰物质的浮选速率常数具有以下形式[16]：

lnKn=Y1-C1·Xn

(3)

其中，n表示入料的第n个粒度；Xn表示第n个粒度的平均粒度；Kn表示第n个粒度的非灰分成分的速率常数；Y1是Kn对Xn的线性曲线的截距，其定义为Xn、第n个粒度范围内的无灰分的质量分数和75 μm以下的细粒中的非灰分的质量分数的乘积；C1是相同曲线的斜率。所有得到的Kn-Xn曲线的相关系数均大于0.9.

同时，他们还提出了一个模型，考虑了两种条件下最终回收率与颗粒大小之间的关系：

(4)

式中，a和b是根据煤种和操作条件拟合的常数。他们发现，对于煤粉含量不同的入料，该模型对浮选回收率的预测较好。根据该模型，入料中-75 μm粒度的增加会导致浮选速率常数降低。

根据Vanangamudi等人的另一项研究结果，两种煤的非灰分和灰分的回收都遵循一级动力学。他们发现，随着原料中细粒级含量(-75 μm)的增加，最大回收率和一级浮选速率常数降低。这是由于入料煤中粗粒级的产率较低所致。对于第一种煤，当入料中细粒级含量从0增加到27.7%时，精煤最终回收率从83.6%下降到77.1%，一级速率常数从0.065 3 s-1下降到0.047 0 s-1. 当细粒级含量从0增加到27.7%时，粗粒级(355～500 μm)物料的最终回收率从63.2%降到38.1%，浮选速率常数从0.060 5 s-1降到0.033 8 s-1. 中粒级(250～355 μm、150～250 μm和75～150 μm)也表现出类似的趋势，回收率分别下降了16%、5.7%和0.4%. 动力学研究表明，随着入料中细粒级含量的增加，浮选速率常数由0.068 2 s-1降至0.035 6 s-1，由0.073 6 s-1降至0.043 5 s-1，由0.077 9 s-1降至0.052 2 s-1. 结果表明，对于粒度为75～150 μm的中间体，浮选回收率最高，浮选速率常数为一级。

Humeres和Debacher (2002) 研究了在pH值为2～12，以氮气为载气的改进型Hallimond管中粗煤粒的浮选动力学。在127～505 μm，通过改变入料粒度进行了一系列实验，发现一级速率常数可以表示为可分离常数与3个新定义的函数的乘积，这3个函数分别是fD、fV和fpH，它们分别依赖于粒度、气体流量和pH值[17]. 浮选速率常数与粒度呈线性关系，且随粒度的增大呈强负相关。这种函数关系可以写成：

fD=e-1.56·dp

(5)

Abkhoshk等人在间歇浮选槽中研究了粒度对煤浮选动力学的影响。他们使用模糊逻辑模型来预测不同粒度煤的累计回收率。以粒度为独立输入变量，以一级速率常数和最终浮选回收率为输出变量。试验使用5个不同的粒级：0～75 μm、75～150 μm、150～300 μm、300～500 μm和500～800 μm[18]. 发现浮选速率常数和累积回收率与粒度之间的关系是非线性的，可用下列方程描述：

(6)

R∞=-8.890 4·[ln(dp)]2+

92.65·ln(dp)-149.25

(7)

采用模糊逻辑模型，对平均粒径为37.5 μm、112.5 μm、225 μm、400 μm和625 μm的实验结果进行了拟合，R2值分别为0.986、0.993、0.983、0.977和0.972. 在接下来的研究中，Kor等人采用不同的回归分析方法研究了粒度对浮选动力学的影响。对于不同的粒级，二次回归模型比其他的回归模型显示出更好的相关性，这与之前的研究结果是一致的。

2 总 结

煤炭浮选是一个非常复杂的三相过程，涉及许多不同的子过程和相互作用。影响煤浮选动力学的因素很多，其中粒度是最重要的因素之一。粒度对煤炭浮选的影响已被广泛研究，并提出了许多浮选动力学模型。本文浅析了粒度对浮选动力学的影响，并讨论了该领域的研究现状，旨在对煤炭浮选提供有价值的现实指导意义。

根据浮选实践，浮选煤的最佳粒度一般小于0.6/0.5 mm或0.25 mm. 煤浮选细粒级和粗粒级浮选回收率呈现不同的趋势。在75～300 μm的粒度，煤的回收率最高。一般说来，不同煤种和浮选条件下的最佳动力学模型有所不同。研究表明，当浮选粒度在37～375 μm时，浮选速率常数与粒度呈矩形分布的一级动力学模型拟合效果最好。浮选速率常数与粒度有很强的相关性。浮选速率在中等粒度范围内达到最高，而在细粒级和粗粒级范围内浮选速率明显下降。这些趋势可以用细颗粒与气泡的低碰撞效率和粗颗粒的高脱离概率来很好地解释。