基于干扰观测器的六自由度机械臂滑模控制

赵莹莹，杨 帆，马惠雯

（天津城建大学 控制与机械工程学院，天津300384）

随着先进制造业的快速发展，工业机器人已经成为了现代工厂的重要装备，它的出现使得一些简单的重复劳作不再需要普通工人来完成，通过工业机器人可以更加精确完整高效地完成现代化工业流程.

机械臂的给定轨迹跟踪，已经有了很多研究成果.文献[1]采用lypnf原理，在对六自由度机械臂的各关节设计终端滑模控制律的基础上，将复杂机器人模型分解成单关节多变量耦合的SISO系统，再对每个子系统分别控制，证明了所提方案的有效性.文献[2]介绍了两种轨迹规划的方法，验证了五次多项式可以保证机器人平稳运行.对于动力学模型中不确定部分用径向基神经网络来逼近，对于神经网络隐含层的参数利用粒子群算法进行在线调整.通过验证仿真，证明了算法的动态性能稳定和跟踪精度高.文献[3]采用模糊反演控制和自适应迭代学习控制，验证了其控制对象能够在不重复扰动下保持很好的控制精度.文献[4]分别就二阶滑模和非奇异终端控制两种方法，控制五自由度机器人在有限时间稳定.由于有限时间控制方法的收敛时间会随着系统初始值的变化而变化，故而在对时间要求较高的场所性能要求不够.相比于有限时间稳定，固定时间稳定具有收敛时间与系统扰动初始值无关的优点，也就是说其收敛时间存在上界，故固定时间稳定的收敛条件也更加苛刻.

1 KUKA KR6-2机器人动力学模型

本文以KUKA KR6-2工业机器人（见图1）为建模对象，该机器人为六自由度关节式机器人，其六个关节均为转动关节，其连杆1—3的转动关节确定手腕位置，连杆4—6的转动关节确定方位.六个旋转关节可以保证机器人在水平和垂直两个方向自由灵活运动.现代工业化进程中此类机器人已经得到了非常普遍的应用，例如：搬运与装卸，包装及拣选，钎焊、涂漆等.

图1 KUKA KR6-2工业机器人

该工业机器人是6轴数的串联结构，其本体重量235 kg，额定负载为6 kg，工作半径1 611 mm，第一轴至第六轴的关节最大工作范围分别为：±185°、+35°/-155°、+154°/-130°、±350°、±130°、±350°.第一轴至第六轴的关节运行最大速度分别为：156°/s、156°/s、156°/s、343°/s、362°/s、659°/s.

如图1所示，该六自由度KUKA KR6-2工业机器人[5]的动力学模型可以表示为

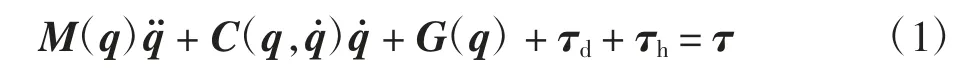
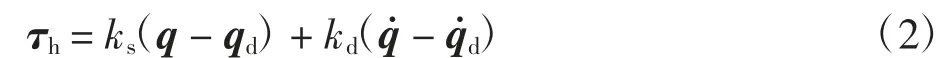
将式（1）中的二阶非线性方程转换为状态空间形式，引入状态变量x=[x1Tx2T]T和期望位置xd=qd，使得x1为关节角度q，x2为关节角速度q˙，则六自由度KUKA KR6-2工业机器人的动力学状态空间方程为

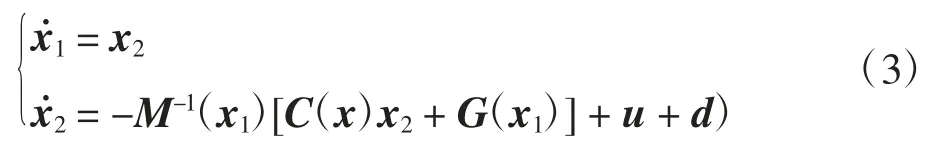
其中：d=-M-1（x1）[τd+ks（x-xd）+kd（x2-x˙d）]为综合干扰项矩阵；u=M-1（x1）τ为系统控制律矩阵.由上述KUKA KR6-2工业机器人模型的表达式可知，六自由度机器人是一个各关节之间存在强耦合，且具有多个变量的非线性系统.

本文所研究的六自由度KUKA KR6-2工业机器人在控制的过程中容易受到诸多不确定因素的干扰，引起系统的不稳定，大大地降低了机器人的性能.本文通过对六自由度机械臂的轨迹跟踪研究，并用观测器的方法，对系统运行中出现的误差进行估计，然后将误差通过反馈给控制器来在线补偿输入，并运用自适应滑模控制方法实现系统的精准轨迹跟踪.控制系统结构如图2所示，其中qd、q分别为KUKA KR6-2工业机器人的期望关节角度和实际的关节输出角度，τ是关节控制力矩，τd属于未知的外部干扰.

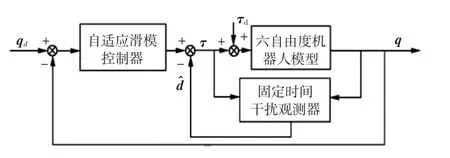
图2 控制系统结构

2 固定时间控制器设计

定义1[6]

针对系统式（3），系统达到平衡点时间T（x0）一致有界，且与系统状态的初始式值无关.即

那么系统在固定时间T（x0）内收敛.

假设1[7]

系统中综合干扰di（i=1，2，3，4，5，6）有界，存在未知常数Di∈R+（i=1，2，3，4，5，6），满足|d˙i|≤Di，即综合干扰有界可导且导数有界.

引理1[8]

非线性系统表达式为

如果存在一个正定连续的函数V（x），满足下式

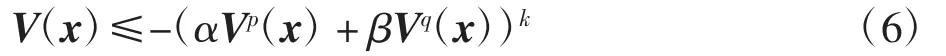
其中α，β，q，p，k∈R+，且pk＜1，1＜qk＜∞，则系统可在固定时间内收敛，且其收敛时间T（x0）满足下式

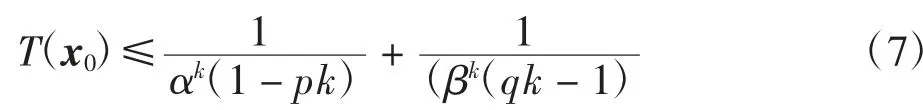
引理2[9]

对于二阶多变量非线性系统

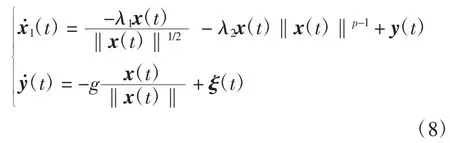
其中：x（t0）=x0；y（t0）=0；参数p＞1；ξ（t）存在上界L.那么x（t），x˙1（t）可以在时间Tmax内快速收敛到原点，且

2.1 固定时间干扰观测器的设计

首先定义干扰观测器ω，在固定时间内实现对系统干扰的准确估计.通过将干扰估计值反馈给控制器达到对干扰在线补偿的目的.

定义速度跟踪误差e1=x1-xd，角度跟踪误差为分别为期望轨迹及其导数，则由系统（2）可得

只需证明s0，可在固定时间内收敛至原点，则d=v0，即综合干扰的估计值.取

2.2 固定时间的自适应滑模控制器设计

根据固定时间观测器式（11）中所得的干扰值d，提出了一种自适应滑模控制，该控制具备指数收敛的优势.控制器设计第一步：建立控制器的滑模面，同时运用指数与等速趋近律，设计指数收敛的滑模控制律，很好地解决了滑模面的趋近问题[12].然后通过对趋近律添加自适应参数来削弱因滑模控制的固有特性所导致的抖振问题，最后对该趋近律的稳定性问题进行了证明.

已知qd∈Rn为关节的期望角度，则期望关节角度与实际关节角度之间的误差可以表示为q~=qd-q，建立滑模面即

根据式（16），设计指数收敛的滑模控制律

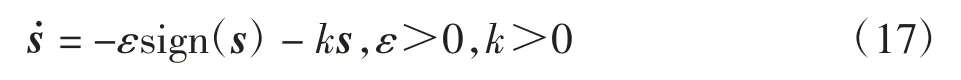
当系统状态不在滑模面附近时，即s→∞，其中ε对趋近律的影响非常小，可忽略，式（17）可以写为

此时，随时间增长，s1→0，也就是说此时系统状态无限接近滑模面.

当系统状态处于滑模面附近，即s→0时，其中参数k对式（18）的影响非常小，可忽略，式（17）可以写为

则系统呈等速趋近律接近于滑模面.对于等速趋近律，当趋近速度增大时，抖振也随之增大；当趋近速度减小时，抖振随之减小，在系统运行的过程中，为了使抖振有效地减小[13]，本文将式（19）中的ε进行了设计，让其可以跟随系统的动态变化自适应地调节ε0，即

3 仿真分析

对KUKAKR6-2机器人进行系统仿真，在MATLAB/Simulink中对图1所示的KUKA KR6-2工业机器人系统进行试验.假设某工业环境中的期望关节角度xd=[xd1xd2xd3xd4xd5xd6]T为xdi=sin（t+iπ/6），i=1，2，3，4，5，6.例如：当i=6时，xd6=sin（t+π）=-sint，即相当于第六个关节在初始状态下转动-180°，该转动角度符合第六个关节的最大转动范围.当系统关节角度初始值设置为x1=[0.1 0.2 0.3 0.4 0.5 0.6]Trad时，对机器人进行系统仿真.为证明式（11）中所设计固定时间干扰观测器ω的收敛特性，引入综合干扰的表达式，即

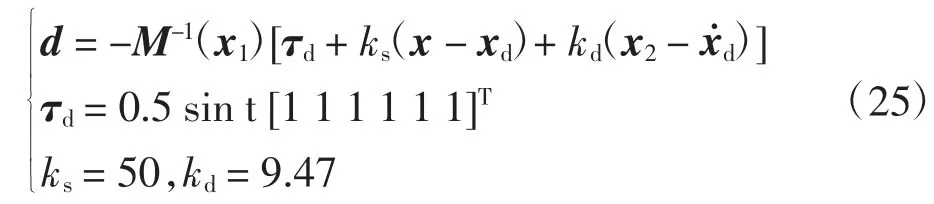
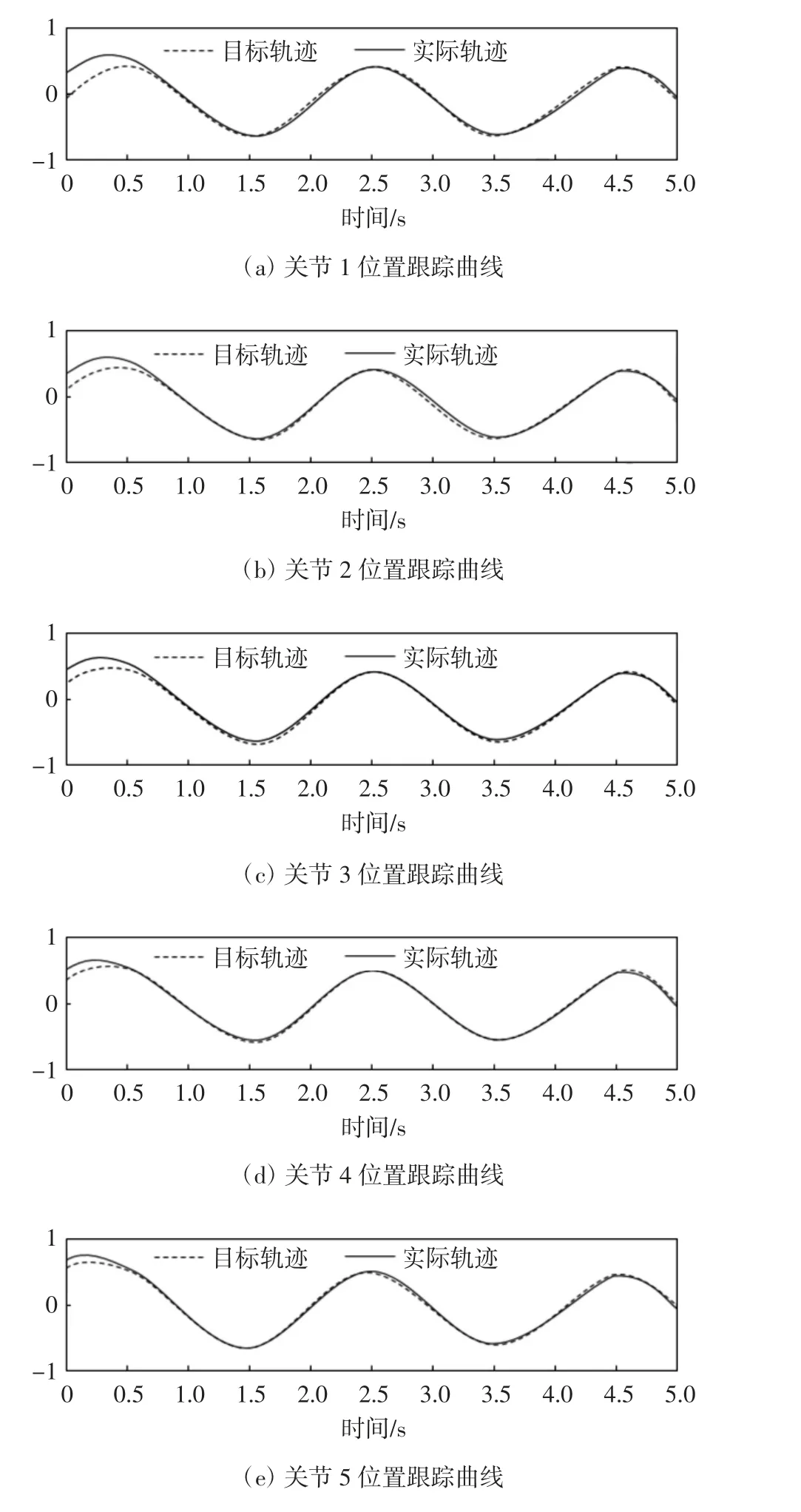
针对系统存在参数不确定及外部干扰的情况下，由图3和图4给出的六个关节位置和速度的期望轨迹跟踪图像，实际位置可以快速准确地跟踪目标位置xd.故本文所提出的固定时间控制策略可以实现对给定期望曲线的准确跟踪且各关节收敛时间较短，位置与速度轨迹跟踪细节曲线分析如图5所示.

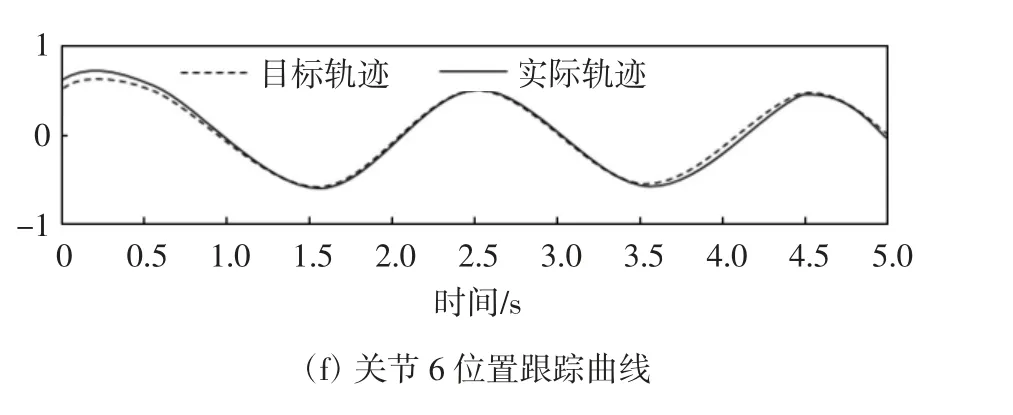
图3 关节1—6位置跟踪曲线

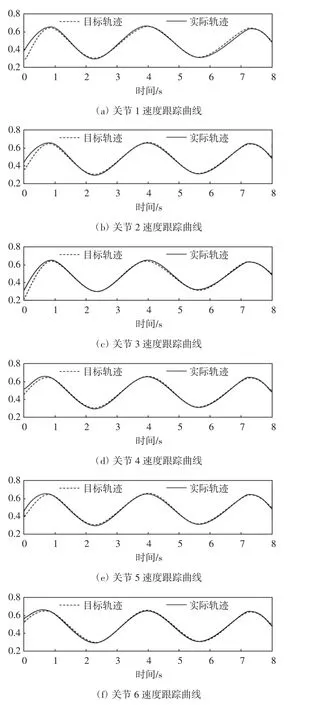
图4 关节1—6速度跟踪曲线

由图5可知：系统跟踪误差最终在T=0.3 s时实现了对给定轨迹xdi=sin（t+iπ/6）的稳定跟踪，且该控制律下的输出轨迹均光滑有界且不存在抖振.通过与文献[15]中的结论做比较，由轨迹跟踪的快速性上就可以看出，固定时间自适应滑模控制相较于固定时间非奇异终端滑模控制的跟踪时间缩短了0.75 s，表明了本文所提出的控制算法的有效性和优越性.

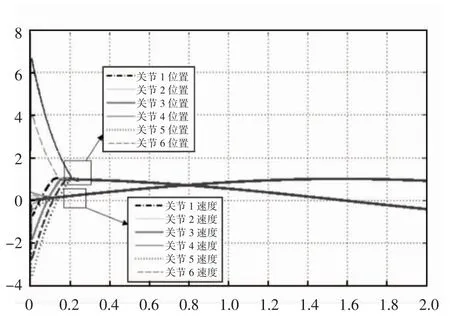
图5 关节1—6速度和位置轨迹跟踪细节曲线

固定时间干扰观测器的观测误差如图6所示，观测误差可快速收敛致原点附近.由图6可以看出，固定时间干扰观测器的观测误差可以在T=0.15 s内收敛到原点附近，也就是说该观测器可以对误差进行准确的估计.

图6 固定时间干扰观测器的观测误差

本文所设计的固定时间干扰观测器相较于有限时间干扰观测器的显著优势在于扰动估计误差不受初值影响.现给定误差初值ε1=100、ε2=50和ε3=25，不改变观测器其他参数的情况下，对收敛效果进行比较.有本文引理2和式（15）的证明可知，不论误差初值为何值，系统的收敛时间总是不受影响.图7为固定观测器在三种不同误差初值时的收敛效果对比图.从图中可知不同初值下的扰动跟踪误差均在0.1 s附近收敛至0.所以可证明固定时间观测器估计误差有上界，并且对估计误差的收敛效果不受误差初值影响.

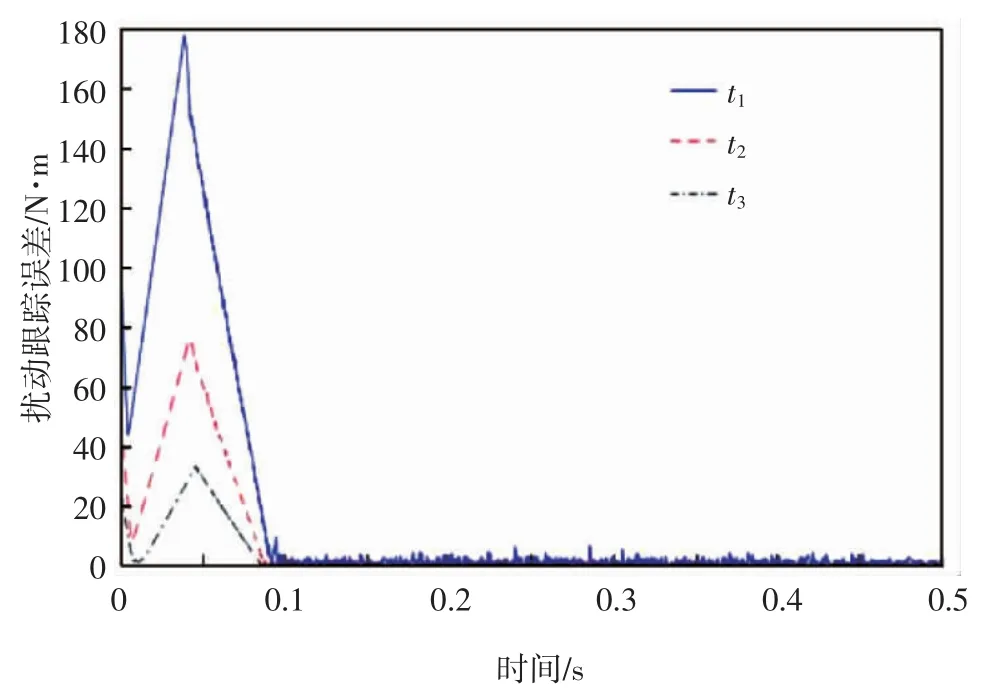
图7 固定时间观测器扰动估计误差收敛效果

4结论

针对外部干扰及参数不确定条件下六自由度KUKA KR6-2工业机器人系统对期望关节角度的速度和位置跟踪问题，本文提出了一种基于干扰观测器的固定时间控制方法，设计了自适应滑模控制器对关节实时位置和速度进行轨迹跟踪.通过验证，仿真结果表明，本文所提出的控制策略，可以在固定时间里实现对期望轨迹的快速精准跟踪，大大地提高了系统的抗干扰能力，保证了系统的稳定运行.