B-P混杂纤维沙漠砂混凝土深梁受剪分形特征
罗 玲,李 桐,刘雪梅,王 博
(1.新疆大学 建筑工程学院,新疆 乌鲁木齐 830047;2.新疆土木工程技术研究中心,新疆 乌鲁木齐 830047)
0 引言
分形几何学使用分数维来刻画分形集的复杂性[1],与传统欧氏几何学的一维、二维及三维描述事物有所不同,分形维数越大,被描述对象越不规则越复杂。对于钢筋混凝土结构,其表面裂缝的发育情况直接影响建筑结构的力学性能[2]。目前,国内外学者对混凝土表面裂缝进行了大量研究。文献[3]研究了钢筋锈蚀对混凝土裂纹的产生及发展的影响,通过多向布筋改变了裂缝的发展方向。文献[4]研究了不同种类不同尺寸纤维对钢筋混凝土梁的抗剪性能影响及梁表面裂缝形态的发展规律。文献[5]进行了配筋混凝土单轴拉伸试验,研究了配筋参数及保护层厚度对混凝土裂缝宽度及间距的影响。但利用传统的力学分析手段很难对混凝土裂缝损伤进行精确判断。目前,许多学者开始利用分形理论来定量描述混凝土表面裂缝的扩展路径以及发育情况。文献[6-7]运用分形理论对无腹筋混凝土梁受剪性能进行定量描述,探讨了剪跨、配筋率等指标对分形维数的影响。文献[8]对混凝土断裂表面的研究表明,混凝土表面粗糙度与分形维数之间存在相关性。文献[9]研究了新型胶凝复合材料力学行为,发现裂缝路径的分形维数越大,断裂能越高。文献[10]利用立方体覆盖法计算混凝土断面分形维数来分析混凝土断面的粗糙程度。文献[11]将分形理论引入混凝土损伤本构模型中,提出了钢筋混凝土梁的抗弯计算方法。文献[12]以体积掺量以及配筋率为变量进行受弯试验,验证了玄武岩筋废旧钢纤维混凝土梁表面裂缝的分形特征。
目前,国内外对于纤维混凝土已有大量的基础性研究[13-16],但沙漠砂混凝土(desert sand concrete,DSC)由于较差的力学性能与工作性能[17],因而对其研究较少。本文以沙漠砂替代率、纤维掺量及纤维混杂比为变量制作9根深梁,利用分形理论对构件加载全过程中产生的表面裂缝进行定量分析,引入损伤变量研究构件裂缝与损伤变量之间的关系,分析了混杂纤维深梁在剪切破坏下的裂缝发展趋势及裂纹分布规律,研究了混杂纤维梁表面裂缝分形维数与分级荷载、极限荷载、跨中挠度、损伤变量之间的关系。
1 试验概况
1.1 试验原材料及配合比
本次试验所用水泥为乌鲁木齐天山水泥厂生产的P·O42.5R普通硅酸盐水泥,采用短切型玄武岩纤维、聚乙烯醇纤维,长度均为12 mm,纤维性能指标见表1。采用乌鲁木齐本地中粗砂,细度模数2.97,粗骨料为天然卵石,直径5~30 mm,级配良好。沙漠砂取自新疆塔克拉玛干沙漠,平均粒径0.963 mm,细度模数0.855,化学成分见表2。采用乌鲁木齐中建西部建设公司的Ⅱ级粉煤灰。减水剂为聚羧酸型高性能减水剂,减水率为37%。根据本团队前期研究成果[18],选取沙漠砂掺量20%,基体混凝土强度C40,配合比见表3。

表1 纤维性能指标

表2 塔克拉玛干沙漠砂化学成分 %

表3 沙漠砂混凝土基体配合比 kg/m3

图1 深梁尺寸及配筋图
1.2 试验方案
试验共制作9根深梁,根据《混凝土结构设计规范》[19]设计深梁尺寸为1 800 mm×200 mm×500 mm。深梁底部纵筋为6根直径16 mm的HRB400钢筋,梁腹不设架立筋及箍筋,支座外设两根箍筋,深梁尺寸及配筋见图1。纤维体积掺量为0.05%、0.10%、0.15%,混杂比为2∶1、1∶1、1∶2。各试验梁试验参数如表4所示。表4中,PT为普通混凝土深梁,DSC为沙漠砂混凝土深梁,B为单掺玄武岩纤维深梁,P为单掺聚乙烯醇纤维深梁,BP为掺玄武岩-聚乙烯醇混杂纤维深梁。

表4 试验梁试验参数
1.3 试验加载
试验梁采用位移控制方式进行加载,以0.1 mm/min速率进行单调静力加载。试验梁加载装置如图2所示。在正式试验前,先对深梁进行预加载以检查仪器设备的正常工作情况并进行相关的调整,调整完成后卸载并将测点数据置零以准备正式加载。

图2 试验梁加载装置图
2 裂缝分形特征
2.1 分形维数计算
绘制各试验梁在破坏状态下的裂缝图并利用分形维数计算中的盒计数法进行计算。利用网格边长为r×r正方形网格覆盖梁裂缝分布区域,记N(r)为覆盖住裂缝的网格数目。随后改变网格边长r的长度以统计lnN(r),直至r趋近于零。统计各尺寸网格的数据并拟合绘制lnN(r)-ln(1/r)图像,若所得曲线具有线性关系,则裂缝具有分形特征,斜率即分形维数,记为B。
(1)
其中:B为分形维数;r为网格尺寸;N(r)为覆盖住裂缝的网格数目。为防止网格边长取值过小使裂缝失去被覆分形性而不具备解析性,根据文献[20]的研究,确定网格最小尺寸为最大骨料粒径,最大尺寸为平均裂缝间距。故本试验选定网格边长为30~130 mm,尺寸间隔10 mm。
2.2 深梁表面裂缝分形特征
以试验梁BP-1∶2-0.10为例,加载初期试验梁所受荷载较小,受弯区混凝土尚未开裂,试验梁主要以弹性变形为主,内部不断积蓄弹性势能。荷载加载至300 kN附近,此时试验梁达到开裂荷载,试验梁纯弯段底部混凝土达到极限强度,开始出现细微的竖直裂缝,裂缝宽度一般为0.02~ 0.05 mm,如图3a所示。在开裂初期,试验梁表面裂缝发展主要为裂缝的延伸及新裂缝的出现,而裂缝宽度的增长较为缓慢。此阶段试验梁所积攒的弹性势能释放完全后,试验梁随荷载增大而进入塑性阶段。此时,试验梁的变形速率较开裂初期要慢,试验梁表面裂缝进入稳定发展阶段,如图3b所示。当试验梁加载至500 kN时,试验梁表面裂缝进入迅速发展阶段。剪压区混凝土达到开裂荷载,在左支座上方出现数条斜裂缝,并迅速向试验梁顶部及底部延伸并发展成贯穿裂缝。纯弯段及弯剪段虽仍不断有新裂缝产生,但主要表现为裂缝的延伸及裂缝宽度的扩展。此阶段试验梁表面裂缝复杂程度较高,裂缝开展图如图3c所示。试验梁继续加载,剪压区斜裂缝充分发展,裂缝宽度达1.1 mm。纯弯段裂缝只有少量延伸,裂缝高度在梁高1/3~2/3处。当试验梁加载至900 kN附近时,加载点边缘混凝土发生轻微压碎,并不断出现纤维拉断声响。同时,主斜裂缝发展至最大宽度时伴随着一声闷响,剪切段发生滑移,试验梁无法继续承受荷载进而试验结束,试验梁剪切破坏裂缝图如图3d所示。

(a) 初裂阶段
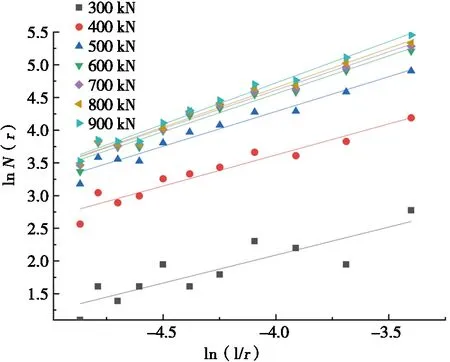
图4 各级荷载下BP-1∶2-0.1试验梁lnN(r)-ln(1/r)曲线
由图3可以看出:受剪试验梁在荷载作用下梁表面裂缝不断延伸扩展,裂缝形状随荷载的增大而不断趋于复杂曲折。利用Fractalfox软件统计并拟合试验梁各荷载等级作用下的lnN(r)-ln (1/r)曲线,如图4所示。由图4可看出:试验梁表面裂缝拟合曲线具有良好的线性相关性,拟合系数为0.872~0.985。并且随荷载的增大,试验梁分形维数也随之增大,与图3所描述的实际试验过程中深梁表面裂缝发展趋势一致,说明裂缝分形维数可准确描述深梁表面裂缝的演化趋势。各试验梁裂缝分形维数变化见表5。

表5 各级荷载下试验梁表面裂缝分形维数
3 分形与荷载关系
3.1 分形维数与分级荷载
深梁裂缝分形维数随荷载变化情况见图5。由图5a可看出:沙漠砂混凝土深梁(DSC)加载后期的分形维数明显低于普通混凝土深梁(PT),但极限荷载最低,裂缝并未充分发展即破坏。如图5b所示,对比不同种类纤维构件,混杂纤维深梁(BP-1∶1-0.1)分形维数明显高于两种单掺纤维深梁,在抑制裂缝发展方面,B-P混杂纤维表现为负混杂效应。由于相较于玄武岩纤维,聚乙烯醇纤维弹性模量较小,在荷载作用下先于玄武岩纤维达到极限拉伸强度而破坏。如图5c所示,对比不同纤维混杂比组,对构件裂缝发展抑制作用最有效组为BP-2∶1-0.1深梁,其次为BP-1∶2-0.1深梁和BP-1∶1-0.1深梁。如图5d所示,在不同纤维体积掺量下,深梁荷载-分形维数曲线相近,曲线差异性不够明显,说明纤维体积掺量对抑制深梁表面的裂缝发展影响较小。
基于图5分形维数-分级荷载曲线进行拟合,得到以下关系式:
B=a-bln(F+c),
(2)
其中:a、b、c均为参数;F为荷载。深梁分形维数-分级荷载曲线拟合系数见表6,由表6可见分形维数与分级荷载成对数关系,且拟合程度较高,拟合系数均在0.94以上。
3.2 分形维数与极限荷载
绘制各深梁盒尺寸与盒计数图,如图6所示。lnN(r)-ln (1/r)保持良好的线性关系,说明深梁表面裂缝与加载阶段一样在极限荷载作用下仍具有分形特征。

(a) 对照组

表6 深梁分形维数-分级荷载曲线拟合参数
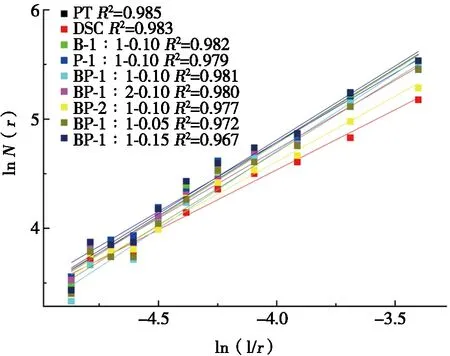
图6 极限荷载作用下深梁表面裂缝ln N(r)-ln (1/r)图
图7为极限荷载作用下的各深梁分形维数。沙漠砂混凝土深梁(DSC)承载力较低,裂缝未充分发展即破坏,故其分形维数最低为1.117。相较于两种单掺纤维构件,B-P混杂纤维深梁分形维数最高。对比不同纤维混杂比深梁,BP-2∶1-0.10深梁分形维数最小,其次是BP-1∶2-0.10深梁,最后为BP-1∶1-0.10深梁,反映出不同混杂比深梁对裂缝发展的抑制作用,并且与上文结论一致。极限荷载状态下,随纤维体积掺量的增大,深梁的分形维数呈先增大后减小的趋势,体积掺量0.05%时分形维数最小。

图7 极限荷载作用下深梁表面裂缝分形维数
3.3 分形维数与跨中挠度
通过现场试验采集的试验梁跨中挠度数据,计算并拟合各深梁分形维数-跨中挠度曲线,如图8所示。从各深梁拟合图发现分形维数与跨中挠度曲线呈现较好的对数关系。如图8a所示,随着深梁挠度的增加,深梁表面裂缝分形维数前期增长速率较快,而后期增长速率趋于平缓,相较于沙漠砂混凝土深梁(DSC),各纤维混凝土深梁挠度均明显增大,纤维的掺入有限地改善了受剪深梁的延性性能,并且比普通混凝土深梁(PT)曲线更趋于平滑。对于不同纤维种类的深梁(如图8b),混杂纤维组深梁分形维数均高于两种单掺纤维深梁,但后期曲线曲率相对较低,破坏时跨中挠度均大于两种单掺纤维深梁。如图8c所示,在不同混杂比深梁中,在极限荷载相的情况下,BP-1∶2-0.10深梁分形维数高于BP-2∶1-0.10深梁,说明玄武岩纤维对裂缝抑制效果优于聚乙烯醇纤维,构件BP-1∶1-0.10分形维数最大,但其极限荷载比前两者都大。由图8c可知:不同纤维体积掺量构件的曲线走势基本相似,随纤维体积掺量的增大,分形维数呈先增大后减小趋势。 对数据进行拟合得到以下关系式:
B=d-eln (ω+f),
(3)
其中:d、e、f为参数;ω为试验梁跨中挠度。各深梁分形维数-跨中挠度曲线拟合参数如表7所示,由表7可知:各深梁拟合程度较高,呈良好的对数关系,拟合系数均在0.94以上。

(a) 对照组
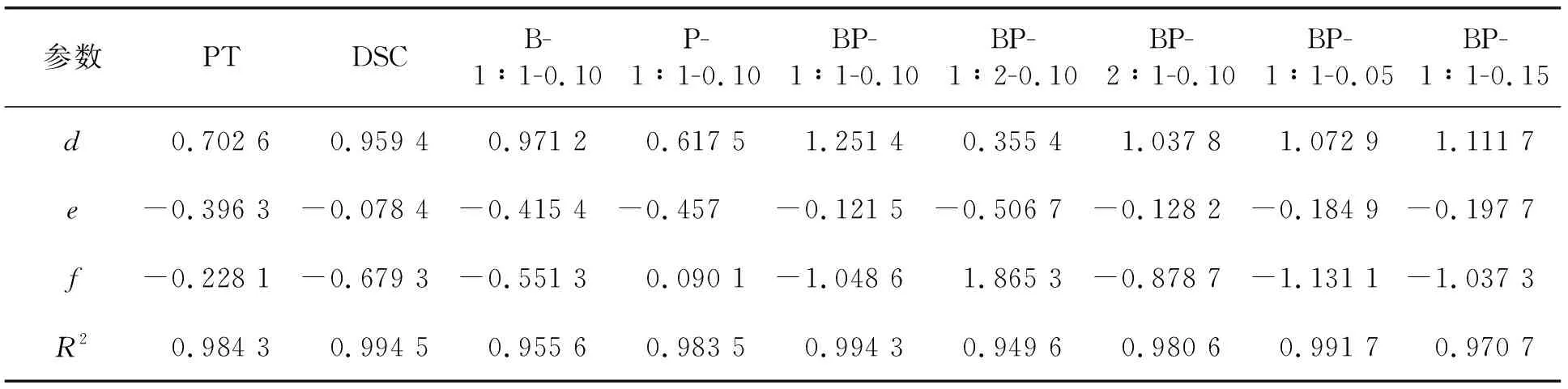
表7 各深梁分形维数-跨中挠度曲线拟合参数
4 分形维数与损伤变量
对于材料因裂缝而引起的损伤,可以借助材料弹性模量的降低来对其进行定量分析。而对于钢筋混凝土构件来说,深梁刚度与材料的弹性模量一样,均可表示物体的变形能力。因此,本试验深梁的损伤变量可表示为:
(4)
其中:D为损伤变量;K0为深梁开裂前的刚度,K0=F0/Δ0,Δ0为深梁开裂时的挠度;K为深梁开裂后的刚度,K=F-F0/Δ-Δ0;F、F0为荷载。
为研究深梁分形维数与损伤变量之间的关系,将深梁各级荷载下损伤变量随分形维数的变化绘于图9。

(a) 对照组
从图9中可以看出:各组深梁分形维数B与损伤变量D之间成指数关系,对其数据进行拟合得到以下公式:
D=e(g+hB+iB2),
(5)
其中:g、h、i均为参数;D为损伤变量。深梁分形维数-损伤变量曲线拟合参数见表8,由表8可知:深梁的损伤变量与分形维数具有良好的指数关系,且拟合程度较高。分形维数可定量表征深梁表面裂缝发育情况以及复杂程度,还可间接表征深梁内部损伤程度。在加载的过程中,深梁表面裂缝的复杂程度与其内部的损伤程度同步增大,且随荷载的增大曲线曲率呈现不断上升趋势。因而,可以通过计算深梁表面裂缝分形维数对其内部损伤程度进行定量分析。

表8 深梁分形维数-损伤变量曲线拟合参数
5 结论
(1)纤维的掺入极大地影响了深梁表面裂缝的发展,在抑制裂缝发展、改善构件破坏形式等方面起到积极作用。
(2)混杂纤维沙漠砂混凝土深梁表面裂缝在分级荷载、极限荷载状态下都具有明显的分形特征。可以利用分形维数对其表面裂缝的复杂程度与不规则性进行定量分析。
(3)混杂纤维沙漠砂混凝土深梁表面裂缝分形维数与分级荷载、跨中挠度呈对数关系,且拟合程度较高。纤维种类对分形维数的影响较大,而纤维体积掺量对分形维数的影响较小。
(4)混杂纤维沙漠砂混凝土深梁表面裂缝分形维数与损伤变量间存在指数对应关系。可通过对深梁表面裂缝分形维数的分析,为结构内部损伤进行定量分析。

