超长拉索多模态控制的黏滞阻尼器参数优化研究

杨 超，陈政清，华旭刚，黄智文，王亚飞

（1.湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙410082；2.柳州东方工程橡胶制品有限公司，广西柳州545025）

引言

桥梁斜拉索因为刚度低、自重轻和内阻尼低等特点，极易发生不同程度的风振、风雨振和参数振动等。作为斜拉桥的一种主要受力构件，拉索发生振动可能会影响桥梁的安全，引发民众的恐慌，严重影响桥梁的正常修建和运营。因此，拉索振动控制是斜拉桥研究工作的重点之一。

各种拉索振动形式中，风雨振普遍被认为是最常见且危险的［1-3］。自Hikami等［4］在日本名港西大桥观测到拉索风雨振之后，该问题逐渐被重视，多位学者从理论、试验和现场观测等不同角度对该问题进行了研究［3，5］。尽管振动机理仍然未有定论，但已有的研究足以总结风雨振具有如下特点：风速约为5-20 m/s；典型振幅约为拉索直径的2倍，但也观测到达到7倍索径的振幅；典型振动频率约为0.6-3 Hz，但也曾出现过超过3 Hz的情况［5-6］。传统中、短拉索自振频率铰高，风雨振的典型振动频率与拉索前几阶频率对应，因此，目前拉索风雨振控制主要关注前几阶模态。

此外，已知的拉索振动形态还包括参数共振、尾流驰振、涡激共振等［6-9］。涡激共振即为风流经过拉索时，Karman旋涡的脱落频率与拉索某阶固有频率相接近而引起的共振。根据Karman旋涡脱落频率与实际拉索振动频率的对应关系发现，拉索低阶涡激共振对应的临界风速都非常低，湍流度较大，而且Griffin等［10］认为，涡激振动的振幅通常会非常小。因此斜拉索的高阶模态涡振问题未受到工程界的关注。

对于低阶模态的大幅风雨振，目前的研究和工程实践已足够表明，在斜拉索锚固端附近安装外置阻尼器是一种较为有效的减振方式。而Pacheco等［11］提出的拉索外置线性黏滞阻尼器的参数优化通用设计曲线和Krenk［12］给出的阻尼器参数优化理论公式一直被沿用至今，并取得不错的实践效果。拉索垂度、弯曲刚度、倾斜等因素对拉索-阻尼器系统的影响，也已被学者分别考虑［13-16］。

总的来说，目前的拉索振动及其控制研究主要关注低阶模态的风雨振，而较高阶模态振动很少受到重视。因此，传统拉索阻尼器的参数设计也以控制前若干阶模态为依据。然而，随着对拉索振动问题的研究不断深入，一些新的振动特征被发现。如Gao等［17-18］的风洞试验结果显示了高阶风雨振发生的频率可能达到6 Hz以上，且随着斜拉桥的跨度越来越大，拉索长度也越来越长，如多多罗大桥的最长拉索为462 m［19］，苏通大桥的最长索达到577 m［20］，俄罗斯Russkij大桥的最长拉索达到578 m［21］。索长的增加导致拉索的基频降低，拉索振动的模态特征也可能发生变化。从模态阶数来看，即使振动频率没有显著增加，超长拉索风雨振发生的阶数仍远高于中、短型拉索。此外，一直被忽视的拉索高阶涡振，近年来也已被注意到。如对多多罗大桥的观测显示，索端不设阻尼器时，在5 m/s的常见风速下涡振频发，最大振幅约2.5 cm［19］。Chen等［22-23］对金塘大桥的拉索振动响应进行了观测，发现其中某根拉索在4-6 m/s的较低风速下频繁发生多模态高阶涡振，并通过数值模拟对不同风速下拉索单个模态或多模态涡振问题进行了研究。苏通大桥采用外置阻尼器与表面凹坑气动措施同时控制拉索振动，却仍然长期存在高阶涡振问题。随着外置阻尼器的老化，涡振问题日渐严重，并开始发生风雨振。超长拉索的涡激振动频率高，产生的加速度巨大，且因其对应的锁定风速较低，发生的频次远高于风雨振，可以预计涡激振动也将对超长拉索的安全、耐久性产生严重的威胁。因此，仅关注拉索前几阶模态控制的阻尼器参数方案可能不再满足要求，同时对超长拉索风雨振与高阶模态的涡振进行控制是有必要的。

本文对苏通大桥斜拉索的振动响应进行了为期15天的现场观测，发现高阶涡振和3 Hz左右（对应拉索约第10-15阶模态）的风雨振问题都非常突出。基于现场实际观测数据，提出同时控制超长拉索风雨振和高阶涡振的阻尼器参数方案。

1 超长拉索振动响应现场观测

苏通长江公路大桥位于江苏省苏州和南通之间，是沈海高速跨越长江的通道，大桥轴线约为南北走向。主桥为1088 m的双塔双索面斜拉桥，最长拉索577 m，是全球首座跨度超过千米的斜拉桥。为监测大桥及拉索的运行状态，苏通大桥安装了健康监测系统，该系统分别在南塔、北塔和主跨跨中桥面上游、下游布置了二维风速监测仪进行风速、风向的实测。风向角0°对应北风，90°对应东风。

为研究超长拉索在不同风况下的响应状态，本文在NJU30号拉索上距桥面15 m高处安装了加速度传感器，在拉索外置阻尼装置发生损坏失效的状态下，对NJU30号索（拉索参数见表1）的响应情况进行为期15天的观测，观测期包括了台风“温比亚”经过当地的过程。

表1 NJU30号索参数Tab.1 Parameters of cable NJU30

1.1 常见风速下涡振响应观测

图1和2列举了某一天24 h内，在不超过10 m/s的常见风速下，NJU30号索的响应情况。

从图1和2可以看出，在正常工作状态下拉索未发生明显振动时，NJU30号索面内、面外加速度响应通常在1 m/s2以内，面内加速度通常略大于面外加速度。在约2∶00-7∶00时段内，桥面风速约为4-7 m/s，风向角约为90°，即风向与苏通大桥轴线垂直时，拉索加速度响应远大于其他时段，发生了明显的涡振。从时程图来看，面内响应大于面外响应，面内加速度响应幅值最大接近5 m/s2，面外加速度幅值响应约为面内的50%；从频谱图来看，振动主要分布在约2-6 Hz，对应拉索第9-25阶模态。

图1 苏通大桥风速和风向（常见风速）Fig.1 Wind speed and wind direction of Sutong Bridge（common wind speed）

1.2 台风下风雨振响应观测

2018年8月17日，2018年第18号 台风“温 比亚”经过苏通大桥，各拉索发生了较明显的振动，于约上午9∶00-10∶00时段，拉索响应幅值达到最大。据现场观察，在该时段内大风伴随强烈的降雨，导致苏通大桥多根拉索以超过本身索径的振幅在面内面外同时发生强烈振动。以上特征可以判断这次振动现象属于风雨振。图3为9∶00-10∶00时段桥面和塔顶的风速、风向，图4为NJU30号索响应情况。

由图3可以看出：上午9∶00-10∶00时段，苏通大桥桥面上游侧平均风速为20 m/s，南塔塔顶平均风速约为35 m/s。风向角约为90°（即垂直于大桥轴线方向）。图4显示：台风引起拉索强烈的振动，面内及面外加速度都比正常工作状态放大数十倍，超过传感器20 m/s2的量程。面内及面外响应频率基本相同，主要发生在3.08 Hz附近，对应拉索第10-15阶模态。与根据以往中、短型拉索风雨振观测得到的0.6-3 Hz的典型频率相比，频率稍微偏高。而从模态阶数来看，由于基频低至0.3 Hz以内，500 m以上超长索发生风雨振的模态远高于以往中、短型拉索的观测结果［3，5］。

图2 NJU30号索加速度响应（常见风速）Fig.2 Acceleration responses of cable NJU30（common wind speed）

图3 苏通大桥风速和风向（2018.8.17，9∶00-10∶00 a.m.）Fig.3 Wind speed and wind direction of Sutong Bridge（2018.8.17，9∶00-10∶00 a.m.）

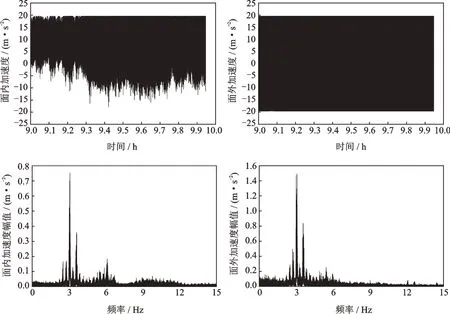
图4 NJU30号索加速度响应（2018.8.17，9：00-10：00 a.m.）Fig.4 Acceleration responses of cable NJU30（2018.8.17，9：00-10：00 a.m.）

2 黏滞阻尼器对拉索的附加阻尼比

现场观测结果显示苏通大桥500 m以上超长拉索的涡振和风雨振主要发生在10阶模态以上。在拉索锚固端附近安装黏滞阻尼器为拉索提供足够的附加阻尼比是一种普遍且有效的控制方式。本节将对拉索-黏滞阻尼器系统的模态阻尼比进行分析。

忽略拉索自身的抗弯刚度、斜度、阻尼以及垂度，建立拉索-阻尼器系统力学模型如图5所示，运动方程为

图5 拉索-阻尼器力学模型Fig.5 Mechanical model of cable-damper

式中T为索力，v为拉索竖向位移，m表示拉索每延米质量，c为黏滞阻尼器的阻尼系数，t表示时间，x为拉索某点离左锚固端的距离，δ（x）为狄利克雷函数，当x-a=0时δ（x-a）=1，当x-a≠0时δ（xa）=0。

2.1 复频率方程

采用分离变量法对式（1）求解，假定

式中i2=-1，ω表示复频率，同时包含了频率和阻尼比的信息

式中ζn表示模态阻尼比。将式（2）分段代入式（1），并引入复波数β=ω（m/T）0.5可以得到式中x′为拉索某点离右锚固端的距离。

式（4）为二阶常微分方程，用三角函数表示其通解为

考虑边界条件φ（0）=φ（l）=0得B=B′=0，可知模态函数为两段正弦曲线

再考虑拉索上阻尼器安装点x=a处的竖向力平衡条件（如图6所示）可得

图6 拉索、阻尼器连接处受力示意Fig.6 Forces of the installation location of the damper

将式（2）和（6）代入式（7）并化简可得

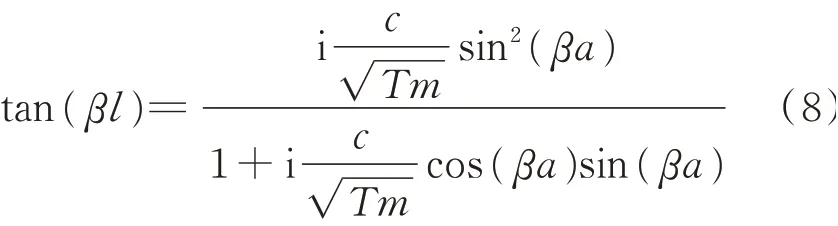
式（8）即为拉索-黏滞阻尼器系统的复频率方程，通过求解复波数β即可得到模态阻尼比。

2.2 附加模态阻尼比

如Krenk［12］所述，可以采用迭代法对式（8）进行求解得到附加模态阻尼比，但多次迭代的方法比较复杂。考虑到实际工程中阻尼器只能安装在距离下锚固端较近的位置，且以往的阻尼比计算通常仅针对前几阶模态，Krenk基于na/l＜1/4的假设条件对式（8）进行了求解，并得到了关于模态阻尼比的渐进表达式。但渐进解显然不适用于求解高阶模态阻尼比。因此，本小节将在不考虑前述假设条件的前提下对式（8）求解。

考虑到实际工程中，结构阻尼比普遍比较小，即使安装了外置阻尼器，拉索的阻尼比也很难达到2%。若忽略阻尼的影响，拉索的频率为

将式（9）代入式（8）等号右边得

其中

式中η=c/（Tm）0.5是阻尼系数的无量纲量。因此，第n阶模态阻尼比可以表示为

对于复数z，有

因此，式（12）可以变化为

再根据

这里，Arg（）表示幅角主值函数。

可以得到模态阻尼比为

或者

为了对式（17）进行验证，分别采用渐进公式、迭代法以及本文式（17）计算拉索-黏滞阻尼器系统前30阶附加模态阻尼比，其中，迭代解可以被视为准确结果。设置迭代过程的结束条件为两个相邻迭代值之间的相对误差小于1%，选取无量纲阻尼系数为η=0.67，当阻尼器分别安装在a/l=2%，5%和10%时的模态阻尼比如图7所示。从图中可以看出，当阻尼器安装在a/l=2%时，通过渐进公式可以得到大约前20阶模态阻尼比的准确结果。但随着安装位置的增加，渐进公式的适用范围越来越小。当阻尼器安装在a/l=5%或10%时，分别仅有前10阶和前5阶的渐进解能够与迭代解相接近。而通过本文式（17）得到的模态阻尼比在算例所有工况下都与迭代解基本一致。

图7 取η=0.67、阻尼器分别安装在a/l=2%，5%和10%时的前30阶模态阻尼比Fig.7 Modal damping ratio of the first 30 modes by setting η=0.67 for a/l=2%，5% and 10%

2.3 附加模态阻尼比的优化

要使某阶模态阻尼比达到最优，应满足方程

将式（14）代入式（18）可得

将式（11）代入式（19）并化简得到

式（20）为关于η的一元二次方程，取正数解并化简为

式（21）即为第n阶模态最优阻尼系数。将式（21）代入式（17）可得第n阶最优模态阻尼比为

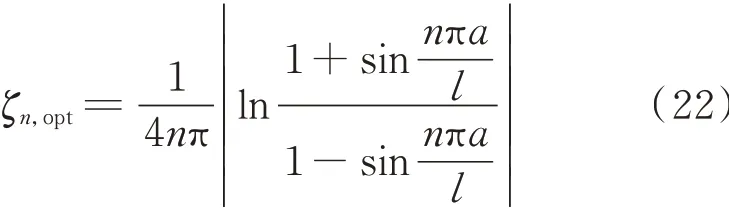
图8对式（21）的准确性进行了验证。选取a/l=1%，计算了第3，20以及40阶模态阻尼比随无量纲阻尼系数η的变化曲线，并将根据式（21）计算的第3，20以及40阶最优阻尼系数η3，opt，η20，opt和η40，opt标记在横坐标轴上。从图中可以看出，由式（21）计算的最优阻尼系数准确地对应了三条曲线的峰值点。由此可知，式（21）能够准确计算包括高阶模态在内的各阶最优阻尼系数。

图8 选取a/l=1%时，第3，20以及40阶模态阻尼比随无量纲阻尼系数η的变化（最优阻尼系数η3，opt，η20，opt和η40，opt被标记在横坐标轴上）Fig.8 Damping ratios of 3rd，20th and 40th modes against the dimentionless damping coefficients.（optimal damping coefficients η3，opt，η20，opt，η40，opt are marked on horizontal axis）

3 多模态控制拉索阻尼器参数方案

值得注意的是，根据图8可知各阶模态的最优阻尼系数是不相同的，只有当阻尼系数接近于某阶最优阻尼系数时，该阶模态才能获得较大的附加阻尼比。因此，设置不同的阻尼系数将使阻尼比在各阶模态中产生不同的分布。传统的拉索阻尼器设计以提高前几阶附加模态阻尼比为目的，通常采用的参数方案为［24-25］

式中k表示控制的最高阶模态，一般取为3-5，由此 计 算 的 无 量 纲 阻 尼 系 数 约 为η3，opt-η1，opt。而ζmin则表示拉索抵抗风致振动所需的最小阻尼比，通常通过Scruton数来确定。Scruton数（Sc=mζ/（ρD2））是衡量拉索抵抗风致振动能力的重要指标，一般认为当Scruton数大于10时，拉索不再发生风致振动，即

式中ρ，D，m分别表示空气密度、拉索直径和拉索每延米质量。

仍以第1节观测的苏通大桥NJU30号索为例（拉索参数见表1），根据式（24）可以算得NJU30号索所需最小阻尼比为ζmin=3.05‰。由于苏通大桥拉索下端锚固在桥面以下1.296 m，所有阻尼器安装位置已确定在距离桥面垂直高度3.5 m处，本文不再对不同的安装位置进行讨论，根据表1参数可以计算出a/l=2.6%。当采用传统阻尼器参数优化方案控制前5阶模态（即ζ1=ζ5＞ζmin）时，根据式（17）可以算得阻尼系数为12.8×104Ν·s·m-1，并由此计算前20阶模态阻尼比，结果如表2所示（考虑阻尼器效率系数为0.5）。

表2显示：模态阻尼比在第2阶达到最大的6.4‰，此后开始随模态阶数的增加而逐步下降。从第9阶（对应频率2.1 Hz）开始，模态阻尼比将低于3.05‰，将无法保证Scruton数＞10的控制要求。而3-7 Hz是苏通大桥超长拉索发生风雨振及涡振的高风险频段，故以上参数选择将无法有效控制拉索振动。

表2 前20阶模态阻尼比Tab.2 First 20 modal damping ratios

3.1 多模态控制参数方案

传统的拉索阻尼器参数方案无法有效控制超长拉索的高阶振动，为了研究更合理的阻尼系数方案，图9给出了当阻尼器安装在a/l=1%，2%或3%时前30阶无量纲最优阻尼系数。

图9 当阻尼器安装在a/l=1%，2%或3%时前30阶模态的最优阻尼系数Fig.9 The optimal dimensionless damping coefficients of each mode for different value of a/l

从图中可以知道：前几阶模态对应的无量纲最优阻尼系数之间相差巨大，但随着阶数的上升，最优阻尼系数呈下降趋势，更重要的是较高阶模态最优阻尼系数之间的差距相对较小，例如η1，opt与η2，opt相差约两倍，但第10-30阶模态对应的无量纲最优阻尼系数都接近于1。这意味着若以前几阶模态为控制对象，所选择的阻尼系数将远大于高阶模态最优阻尼系数，阻尼器难以为高阶模态提供足够的阻尼比，仅能够控制约前3-5阶的模态范围。若选择较小的阻尼系数，第1，2阶的模态阻尼比可能比较小，但却能使阻尼器控制的模态范围大幅扩大。

对于500 m级以上的超长斜拉索，基频低至0.3 Hz以内，低阶模态对应的涡激共振风速也非常低，第2阶模态对应的涡振风速甚至低于0.5 m/s，风速越低湍流度将越高，以致难以形成稳定的涡激力。再考虑到根据实测研究［26-27］和结构动力学原理，结构固有模态阻尼比与频率呈负相关的趋势，超长拉索的低阶模态存在一定的固有阻尼比。同时，低阶涡振加速度和位移幅值都非常小，几乎不会对拉索及桥梁安全产生威胁。因此，本文认为超长拉索的低阶涡振可以不进行控制。

根据Chen等［3］对洞庭湖大桥拉索数根约100-150 m拉索的长期观测，几乎未发现过1阶风雨振；根 据Zuo等［28］对FredHarton桥 数 根80-200 m拉 索的长期观测，也未见有1阶风雨振的发生；根据Chen等［29］的研究结果，发生风雨振的模态阶数与风速正相关；根据苏通桥500 m级拉索的现场观测，风雨振主要以3 Hz左右的频率，即约第10阶以上模态发生。另外，大幅1，2阶风雨振，将需要伴随大幅度的拉索长度伸长，需要巨大的能量。以上论证及检测数据足以说明，500 m级超长拉索，是无法发生第1，2阶风雨振的。

综上所述，对于超长拉索的阻尼器参数选择，应针对控制第3阶以上模态，以使其控制的模态范围更大。

3.2 案例分析

仍以NJU30号索为例，若按照控制第3阶以上模态的参数方案，即

将式（25）代入式（17），取a/l=2.6%可以计算阻尼系数，并与控制前5阶模态方案进行对比，如表3所示。计算两组参数下，拉索前30阶模态的阻尼比（考虑阻尼器效率系数=0.5），如图10所示。

表3 参数方案对比Tab.3 Comparison of parameter optimization

图10 参数方案对比Fig.10 Comparison of parameter optimization

以上计算可以看出，多模态控制的参数方案设置了较小的阻尼系数，与传统控制前5阶模态的参数方案相比，阻尼系数下降了约5倍。传统的参数方案第2阶模态阻尼比达到最大的6.5‰，并使拉索第1-9阶模态阻尼比满足要求，对应频段为0-2.12 Hz。当模态阶数继续提高时，模态阻尼比急剧下降，无法有效抑制风雨振或者涡振的发生。多模态控制的参数方案放弃对不会发生振动的超低频第1，2阶模态的控制，使第19阶模态达到约12‰，并保证第3-28阶模态阻尼比同时达到目标值，控制范围为0.71-6.58 Hz的频率段。本课题组于2018年12月在苏通大桥选择了7根拉索进行实桥试验，将原控制前5阶模态的阻尼器更换为按照本文参数方案设计的阻尼器，并对这7根拉索的响应情况进行了长期监测：在阻尼器正常工作的情况下，至今再未发现明显的振动问题。

4 结论

针对传统拉索阻尼器参数优化方案无法控制超长拉索高阶振动问题，本文拉索-黏滞阻尼器系统高阶模态的附加模态阻尼比及最优阻尼系数进行了推导，基于现场实测数据，以复模态分析得到的模态阻尼比为控制指标，提出了从第3阶开始考虑风致振动控制的阻尼器参数方案，并与传统方案进行了对比，主要得出如下结论：

1）在不同风雨条件下，苏通大桥500 m以上超长拉索既可能在风雨条件下发生3 Hz左右的风雨振，又面临高阶涡振在常见低风速下频繁发生。

2）500 m级超长拉索的基频低至0.3 Hz以内，从模态阶数来看，不管风雨振还是涡振，超长拉索通常都是以高阶形式发生。传统的阻尼器参数设计方案以前几阶模态为优化对象，产生的控制效果随模态阶数的上升而急剧下降，无法满足多模态振动控制的要求。

3）第n阶模态的最优阻尼系数为1/|sin（nπa/l）|，所以前几阶模态对应的无量纲最优阻尼系数之间相差巨大，但第10-30阶模态的无量纲最优阻尼系数之间的差距较小。

4）当阻尼器的参数方案调整为控制第3阶以上模态时，所需的阻尼系数较传统方案大幅降低，模态阻尼比的最大值大幅提高，阻尼器对超长拉索控制的模态范围大幅增加。