一道模拟题中下滑时间长短的定量比较
陈衍訸 张 旭
(1.柳州高级中学,广西 柳州 545001;2.柳州市第二中学,广西 柳州 545616)
例题.(2019年湖北武汉高三调研)如图1所示,将完全相同的两个小球1、2分别从同一高度由静止释放,其中图1(甲)是一倾角为45°的光滑斜面,图1(乙)为光滑圆弧,不计空气阻力,则下列对四种情况下相关物理量的比较,正确的是
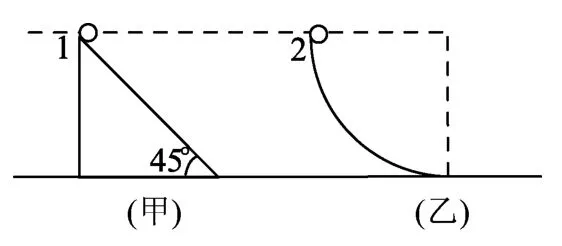
图1
(A)落地时间t1=t2.
(B)全程重力做功W1>W2.
(C)落地瞬间重力的功率P1=P2.
1 试题引起的讨论
该题是2019年湖北武汉高三调研的试题,答案毋庸置疑为(D)选项,但是学生答题后普遍对(A)选项中两球下滑时间长短的比较产生浓厚兴趣.
学生在分析该问题时给出如下的解答:“由动能定理可知,两小球从初始位置到水平面上同一高度处速度大小总相等,但沿圆弧运动的小球路程更长,因此t1<t2.”
这是一种常见的误解,实质上运用了微元法,如图2所示,认为在同一个Δh内速率v相等,而每一个Δh都有对应的斜面下滑的直线距离小于对应的圆弧下滑的弧长距离.但是,通过作图分析,显然在下滑距离较短时AB>A′B′,而在下滑距离较长时有C D<C′D′,并不是每一段直线长都小于对应弧长的.导致这一误解的主要原因是部分学生在看到直线路程小于圆弧路程这个信息时,没能深入分析该物理过程中细致的对应关系,而是仅凭直觉就认为“路程大的运动时间一定长”,从而步入了误区.
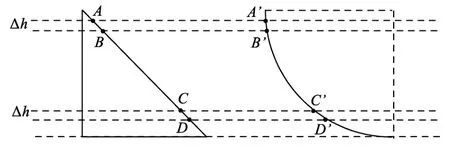
图2
因此,以上的解答是存在明显瑕疵并不严谨的,现假设图甲中下滑时间为t1,图乙中下滑时间为t2,笔者在此给出相关问题的严格证明.
2 用初等数学知识求解
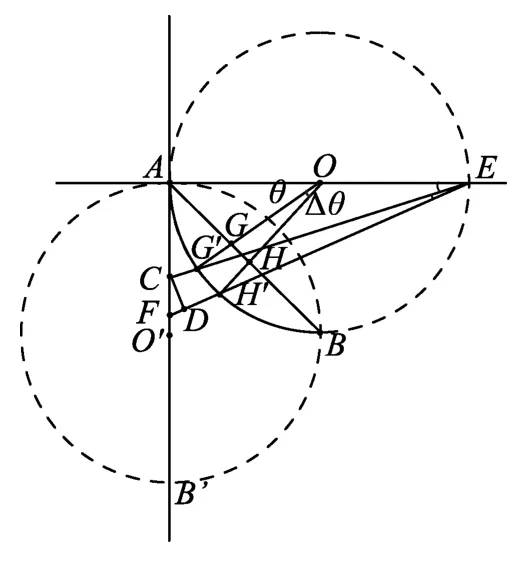
图3
情形1:沿直线A B′下滑的小球,
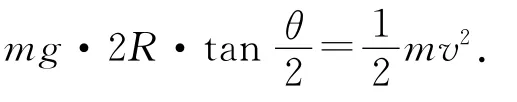
在如图3所示的Rt△CDF由∠ECD接近于直角,则在△ECD中有代入得Δθ.则对应时间为
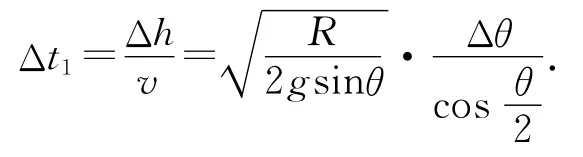
情形2:对沿弧面AB下滑的小球,mgRsinθ=解得则对应时间为
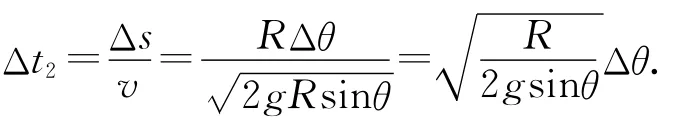
该方法虽然不涉及高等数学知识,但是巧作等时圆,将不易计算的沿斜面下滑时间转为求解沿竖直方向自由落体的时间,化繁为简.
3 用微积分求解
情形1:对沿直线AB下滑的小球:,解得
情形2:对沿圆弧AB下滑的小球,下滑到任意位置P时,有
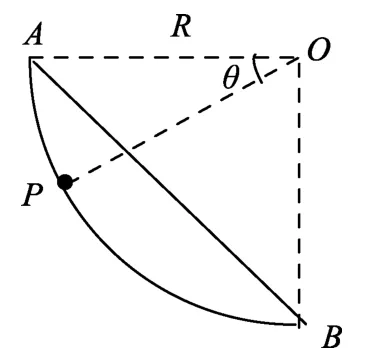
图4
机械能守恒:m g Rsinθ=
左边是一个椭圆积分,没有解析解,可以查表也可以用计算机数值计算.这里用MAT L A B软件计算数值解.解得

通过计算机模拟出数值解解出t1、t2的具体值,从而比较两种情况下的时间长短,结果显示t1>t2,结果同上.

