地下空间结构对邻近地上结构地震反应影响振动台实验
程 业,潘旦光,2,陈清军,付相球,李雪菊
(1. 北京科技大学土木系,北京 100083;2. 城市地下空间工程北京市重点实验室,北京 100083;3. 同济大学土木工程防灾国家重点实验室,上海 200092)
在地震作用下,大型地下空间结构的存在显著地影响邻近场地的地面运动从而影响邻近建筑的地震反应[1−2]。为分析地下空间结构的局部场地效应,及由此导致地上结构地震反应的变化规律,国内外学者分别采用解析解、数值解和振动台实验进行广泛的研究。
Lee 等[3]和梁建文等[4− 6]采用解析法得到弹性半空间中单个洞室、多个洞室的地震反应问题,计算结果表明地下洞室易使邻近场地地面位移幅值增大。地下空间结构、地基土以及邻近地上结构构成了一个复杂的相互作用整体,影响该体系地震响应的因素较为复杂。Guo 等[7]采用广义层间位移谱分析方法研究了地铁车站对地上结构响应的影响,结果表明建筑物自身动力特性和建筑物与车站的间距是关键影响因素。Wang 等[8]采用数值计算方法研究了地下结构-土-地上结构相互作用中地上结构形式、地震波的入射方向、地下结构和地上结构的距离、土体剪切波速、地下结构的埋深等对结构地震反应的影响,而其中地上结构形式和地震波的入射方向是两个最重要的因素。Abate 等[9]对隧道-土-地上结构体系进行了数值分析研究,结果表明浅埋隧道场地表面相比自由场加速度降低,深埋隧道下加速度放大;地上结构位于隧道正上方时地震反应最大,场地对于地上结构输入频率的滤波作用在隧道-土-结构体系中非常重要。Li 和Chen[10− 11]对互相临近的地铁隧道和高层结构模型进行了三维耦合动力分析,研究表明地上结构的存在会降低车站的响应,地铁站和隧道的存在增加了附近地面的峰值加速度。
由于土-结构相互作用体系的影响因素很多且非常复杂,为验证理论模型的有效性,常采用实验进行验证[12−14]。国内外学者在土-地上结构相互作用和土-地下结构相互作用已开展较多振动台模型实验[15−19]。土-地下结构相互作用振动台实验通常侧重于地下结构的动力反应和破坏情况,同时也观察到地下结构对地面运动的影响。Abuhajar等[20− 21]结合离心机振动台实验和数值模拟进行了土-涵洞动力相互作用研究,结果表明土-涵洞相互作用降低了地面的运动输入。陈国兴等[22− 23]研究表明地下结构的对周边土体的地震动频谱特性有显著的影响,在近、远场地震动作用下模型地基土加速度反应的频谱特性和放大效应有显著差异。Chen 等[24]研究发现脉冲形式的输入波增大了地铁站和周围场地的动力响应,这主要是由于其固有的丰富的低频成分和高能量。Wang 等[25]对隧道-土-地上结构的振动台实验研究表明隧道的存在一定程度上阻碍了地震波的传播,从而降低了中低楼层地上结构的地震响应。
为研究地下空间结构导致地震动变化对地上结构地震反应的影响,潘旦光等[26]首先开展了地下结构-土相互作用的振动台实验,实验结果表明在水平地震输入下地下空间结构场地两侧各一倍宽度范围内有明显的竖向振动,且地表水平地震动可达自由场地震动的1.933 倍。邻近地下空间结构的地上结构基础地震输入与直接位于场地上基础地震输入不同,从而导致地上结构地震反应发生改变。为进一步研究地下结构对邻近地上结构的影响,开展了地下结构-土-地上结构相互作用(SSSI)和土-地上结构相互作用(SSI)振动台对比实验。按照几何相似比为1∶30 进行了地上框架结构和地下空间结构的实验模型设计和制作,在同济大学土木工程防灾国家重点实验室的多动能振动台上进行了6 条不同震中距的基岩波在6 个不同加速度幅值下SSSI 和SSI 的振动台模型实验。对比分析了SSSI 体系和SSI 体系下场地及结构动力特性的变化以及地上结构加速度放大系数随输入地震波的频率、幅值等因素的变化规律。在此基础上,分析地下空间结构对地上结构箱基的平动加速度、摇摆加速度和结构变形分量的影响。
1 实验概况
如图1 所示,振动台模型实验共分为两组:1) 地下结构-土-地上结构振动台模型实验(简称SSSI 实验);2) 土-地上结构振动台模型实验(简称SSI 实验)。地下结构原型为一个高15 m、宽27 m的地下三层混凝土结构,断面尺寸为27 m(宽)×15.2 m(高),柱间距为9 m,结构顶部埋深3 m。地上结构原型为一个6 层框架结构,基础为箱型基础,地上部分尺寸为7.2 m×7.2 m×18 m,层高3 m,箱基尺寸为12 m×12 m,深3.6 m。模型箱采用同济大学孙利民等[27− 28]设计的一个长6.5 m、宽1.5 m、高1 m 层状剪切箱。剪切箱共分为9 个滑动层,滑动层之间放置有滑动轴承,箱体两侧通过螺栓固定着一个厚度为2 mm 的钢板,使模型箱产生剪切运动,同时避免箱体扭曲。内壁有一层厚2 mm的橡胶垫,以减少箱体的边界效应。剪切箱固定于振动台台面上,用于研究刚性基岩上单一土层场地土-结构相互作用问题。

图1 振动台实验Fig. 1 Shaking table test
1.1 相似设计
本实验为文献[26]振动台实验的延续,因此,相似比设计相同,其中设计的几何相似比为1∶30,结构材料弹性模量相似比为1∶12,加速度相似比为1∶1,由此可导出时间相似比为0.183,其它相似比详见文献[26]。实验中结构通过添加配重块的方式满足模型相似律。但涉及到土介质的振动台模型实验时,常规条件下的模型相似律因重力场的影响而很难满足,此外,还要考虑材料本构的相似性,这是非常困难的。因此,本实验不追求模型体系和原型体系参数严格的相似,而是为了较好地反映出地下空间结构对于地上结构地震反应的影响,模型土采用频率相似的原则进行设计[29],使模型中地上结构与土层的基频相接近,来探讨地下结构对邻近地上结构地震反应影响的规律。
1.2 结构模型和模型土
地下结构模型采用文献[26]中长1500 mm、宽920 mm、高505 mm 的有机玻璃模型,如图2所示。实测一阶频率为14.14 Hz,二阶频率为57.27 Hz。模型土采用砂和锯末的质量比为3∶1,密度为985 kg/m3的混合土[30]。土层厚990 mm,分20 层装填。
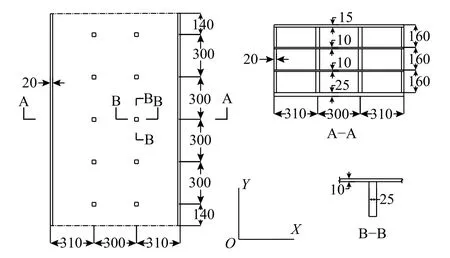
图2 地下结构模型 /mmFig. 2 Underground structure model
框架结构模型平面布置如图3 所示,模型层高100 mm,柱的尺寸为15 mm×20 mm,楼板厚10 mm,框架结构1 层~5 层每层配重质量为3.30 kg,顶层配重质量为2.67 kg。箱型基础尺寸为400 mm×400 mm×120 mm。箱基内部配重质量为31.75 kg,箱基顶板上配重质量为23.52 kg。配重完成后,将箱基底板固定约束下,实测前两阶频率分别为9.97 Hz 和30.18 Hz。

图3 框架结构模型 /mmFig. 3 Frame structure model
1.3 传感器布置及实验加载方案
SSSI 实验和SSI 实验的加速度传感器布置如图4 所示。SSSI 实验中地下空间结构位于土箱中部,地下结构两侧距土箱边缘距离为2.8 m,地上结构位于地下结构边缘一侧0.35 m 位置处。地上结构距离土箱边缘距离为2.05 m,类似于远置人工边界方法进一步减少了土箱边界效应的影响。SSI 实验中地上结构在土箱中的相对位置与SSSI实验中相同。SSSI 实验共布置了61 个加速度传感器,传感器存活率为96.7%,SSI 实验中共布置了56 个加速度传感器,传感器存活率为98.2%。

图4 加速度传感器布置图 /mmFig. 4 Accelerometer layout
实验中选取近震、中震和远震6 条基岩波,它们分别为:1971 年2 月9 日San Fernando 地震距离震中21.5 km Pasadena-Old Seismo Lab 台站的Near-sfern波和130 km Isabella Dam 台站的Far-sfern 波、1989 年10 月18 日Loma Prieta 距离震中43.94 km Belmont-Envirotech 台站的Near-lomap 波和83.37 km Point Bonita 台站的Mid-lomap 波、1999 年9 月20 日台湾集集地震距离震中168.72 km KAU082台站的Far-chichi 波和65.79 km TTN025 台站的Mid-chichi 波。加速度A 幅值为1 m/s2时的时程如图5 所示。Near-sfern、Near-lomap、Far-chichi、Far-sfern、Mid-lomap、Mid-chichi 的卓越频率分别为20.5 Hz、8.1 Hz、2.8 Hz、10 Hz、4.2 Hz 和11.6 Hz。
图5 输入地震波加速度时程Fig. 5 Acceleration histories of input seismic waves
两组实验的加载顺序相同,工况1 和工况2分别为峰值加速度为0.1g的白噪声输入和5 Hz的正弦波,然后进行0.035g、0.1g、0.2g、0.4g、0.6g、0.9g这6 个荷载幅值实验,每个荷载幅值依次进行Near-sfern、 Near-lomap、 Far-chichi、Far-sfern、Mid-loma、Mid-chichi 振动台实验,然后进行0.1g白噪声扫频,共完成44 个实验,其中工况1、工况9、工况16、工况23、工况30、工况37、工况44 分别为各阶段的白噪声工况。
2 振动台实验结果
2.1 SSI 和SSSI 的结构动力特性
两组实验的工况1 的白噪声激振下的框架顶点与输入加速度(SSSI 实验和SSI 实验分别为A33 和A30 的时程)的传递函数如图6 所示。SSSI实验中地上结构的一阶频率为9.25 Hz,二阶频率为32.25 Hz;SSI 实验中地上结构的一阶频率为9.5 Hz,二阶频率为32.5 Hz。相比于底部刚性约束模态实验结果,SSI 实验的一阶频率降低,符合土-结构相互作用对结构动力特性的变化规律。同时SSSI 体系中地上结构一阶频率低于SSI 体系,这表明地下空间结构会影响邻近结构体系的自振频率。图7 为两组实验不同阶段白噪声扫频所得的地上结构自振频率。不同白噪声工况下,结构的自振频率有微小的降低,但变化不大,说明模型土具有良好的弹性恢复能力,结合后面的土层动力特性识别结果可认为结构在整个加载过程为弹性。

图6 框架结构顶部测点传递函数Fig. 6 Transfer function of the top point of frame structure
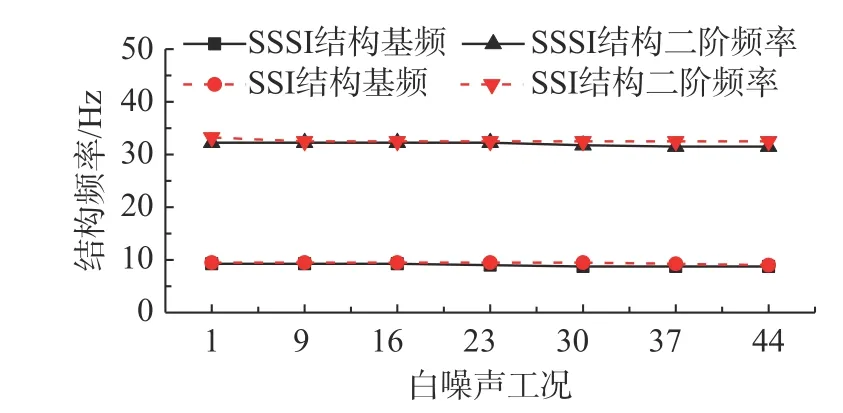
图7 结构自振频率Fig. 7 Natural frequency of frame structure
SSSI 实验中土层表面测点A7 和SSI 实验中土层表面测点A3 与输入加速度的传递函数如图8所示。由此可得SSSI 和SSI 体系中场地的基频分别12.5 Hz 和13.25 Hz。SSSI 体系中场地基频更小,地上结构自振频率的变化说明地下空间结构影响了邻近场地的动力特性并导致邻近结构动力特性的变化。图9 为白噪声下SSSI 实验和SSI 实验各工况识别的场地前二阶频率。当输入波PGA≤0.1g时,场地基频没有发生变化,此时场地土状态基本没有变化;当PGA 达到和超过0.2g之后,场地基频随着PGA 的逐级增高而降低,表明在强震作用下土体进入塑性而导致频率降低,这也将引起结构体系频率的降低。
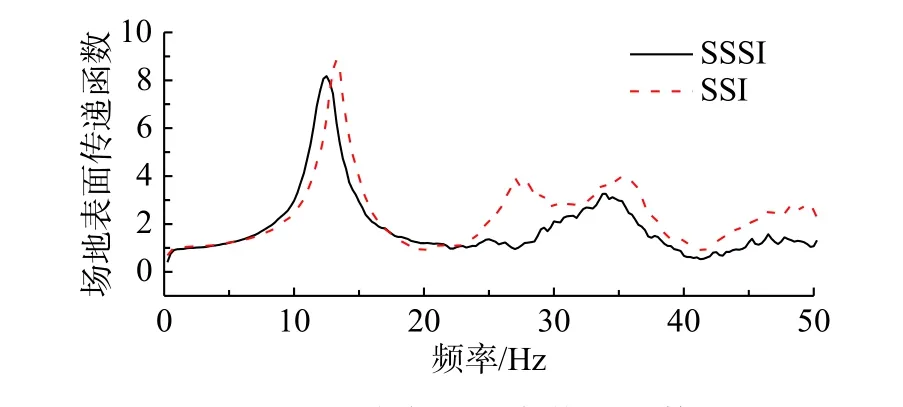
图8 场地表面测点传递函数Fig. 8 Transfer function of site surface
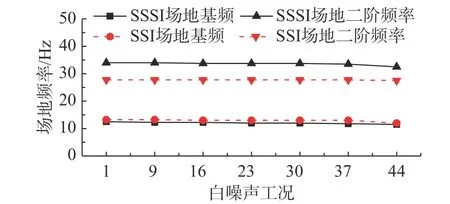
图9 场地自振频率Fig. 9 Natural frequency of site
2.2 加速度放大系数

在0.035g输入地震波下,土层和框架结构加速度放大系数沿高度变化如图10 所示。与输入地震波的卓越频率相比较可知,输入波Near-sfern 的卓越频率高于场地基频,Far-chichi 和Mid-lomap卓越频率低于场地基频,另外三条输入波卓越频率与场地基频接近。当Near-sfern、Far-chichi 和Mid-lomap 输入时框架结构顶端放大系数小于另外三条地震波输入的加速度放大系数。这表明当输入波的卓越频率远大于或小于结构的基频,体系的放大系数都比较小,而当卓越频率与结构的频率接近时,动力放大系数较大。在不同PGA 输入下也可以得到类似的结果。
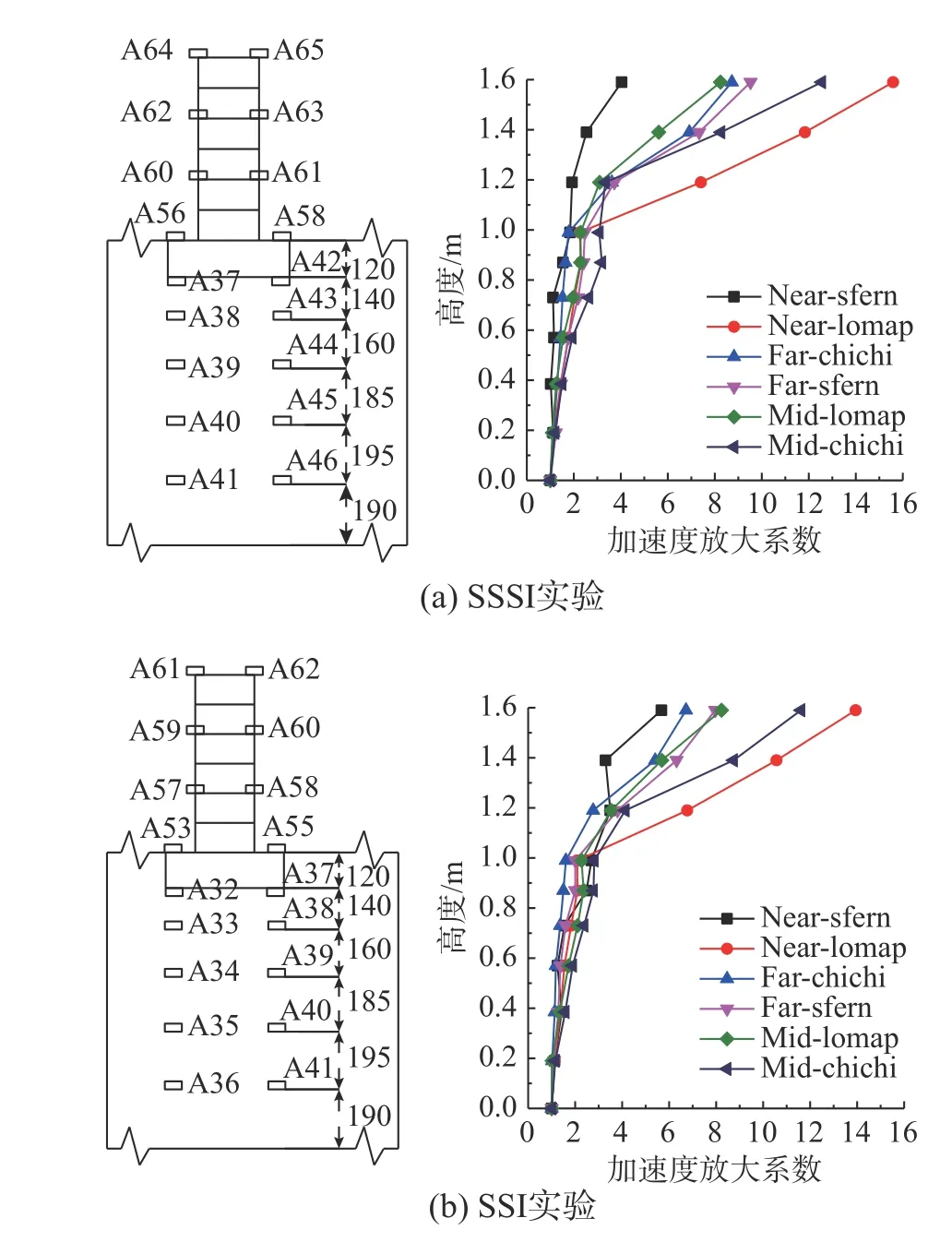
图10 各地震波输入下加速度放大系数(PGA=0.035 g)Fig. 10 Acceleration amplification factor under different seismic inputs (PGA=0.035 g)
图11 为6 条地震波输入下加速度放大系数平均值沿高度变化分布图。SSSI 和SSI 放大系数沿高度的变化趋势是相同的,且加速度放大系数随着PGA 的增加而减小。这表明地震动输入越大,由于非线性使土的剪切模量降低、阻尼增大而导致加速度放大系数更小。在PGA=0.035g和0.9g时,SSSI 的放大系数大于SSI 的放大系数;在PGA=0.1g、0.2g、0.4g和0.6g时,SSSI 的放大系数小于SSI 的放大系数,这表明地下空间结构改变了邻近场地的地面运动,在不同强度地震动输入下,地下空间结构和邻近土的非线性程度不完全相同,由此引起的地面运动非常复杂,这将导致地上结构的反应可能大于也可能小于不考虑地下空间结构影响下的地震反应。
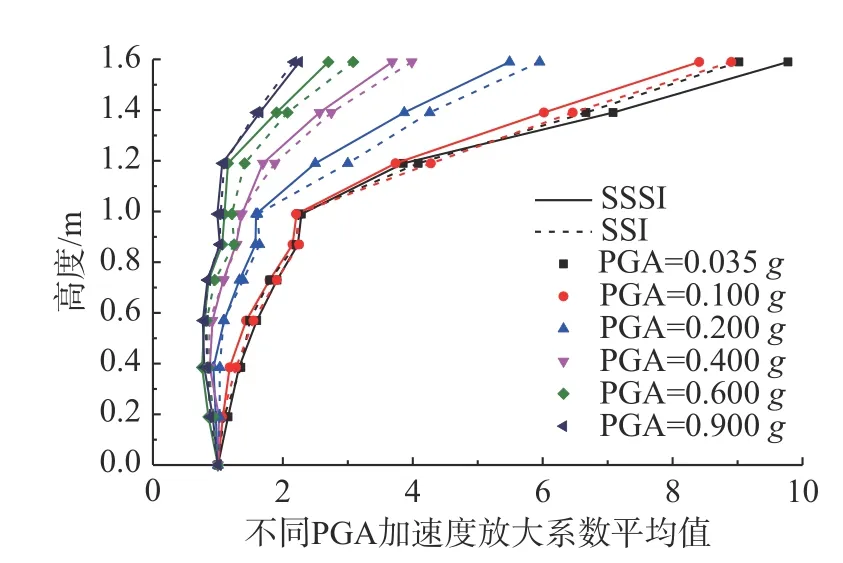
图11 不同PGA 下加速度放大系数Fig. 11 Acceleration amplification factor under different PGAs
3 地上结构加速度反应
3.1 基础加速度反应
箱型基础的加速度反应包括平动分量u¨g和摇摆分量θ¨。结合实验的传感器测量结果,SSSI 实验和SSI 实验基础的平动和摇摆加速度可表示为:

6 条地震波下箱基u¨g和Hθ¨的放大系数平均值u¨g/a0,max和Hθ¨/a0,max如表1 所示,表1 中H表示地上结构的高度,Hθ¨/u¨g表示平动分量与转动分量之比。实验结果表明:对于基础的平动加速度,两组实验的放大系数比较接近,而对于摇摆加速度,SSSI 实验大于SSI 实验。地上结构对于土-结构相互作用体系存在惯性相互作用,所以,对于均质土层的SSI体系,箱基的摇摆加速度分量主要是由惯性相互作用引起的。而SSSI 体系邻近地下空间结构的场地的地面运动不同点存在显著差异,且存在竖向振动[26],这导致SSSI 体系中上部结构和土之间不仅存在惯性相互作用,而且,存在运动相互作用,由此,SSSI 体系基础的摇摆分量大于SSI 体系。

表1 箱基加速度放大系数Table 1 Acceleration amplification factor of box foundation
从Hθ¨/u¨g的角度看,随着输入地震波幅值的增加,Hθ¨/u¨g逐渐增大。SSSI 实验和SSI 实验的箱基摇摆分量与平动分量之比Hθ¨/u¨g在0.035g时分别为0.691 和0.521,而在0.9g时分别达到了2.174和1.763,这是由于强震作用下土体进入非线性,从土层底部传播到地表的加速度放大系数减小,所以,平动分量u¨g的放大系数随着PGA 的增加而减小。在强震导致土体刚度降低时,上部结构的惯性相互作用并没有降低,由此引起摇摆分量θ¨的放大系数随着PGA 的增加而增大,这说明在强震作用下,箱基的转动影响更强。而且SSSI 体系的Hθ¨/u¨g比SSI 的大,因此,对于地下空间结构场地,上部结构将承受更大的摇摆地震动输入。
3.2 结构顶端加速度反应
由于箱基存在平动和摇摆分量,则图12 中的地上结构任意高度h处的加速度反应u¨可以表示为[31]:
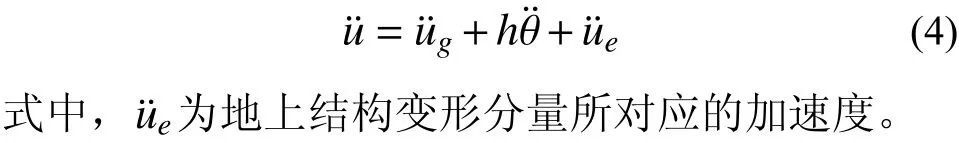

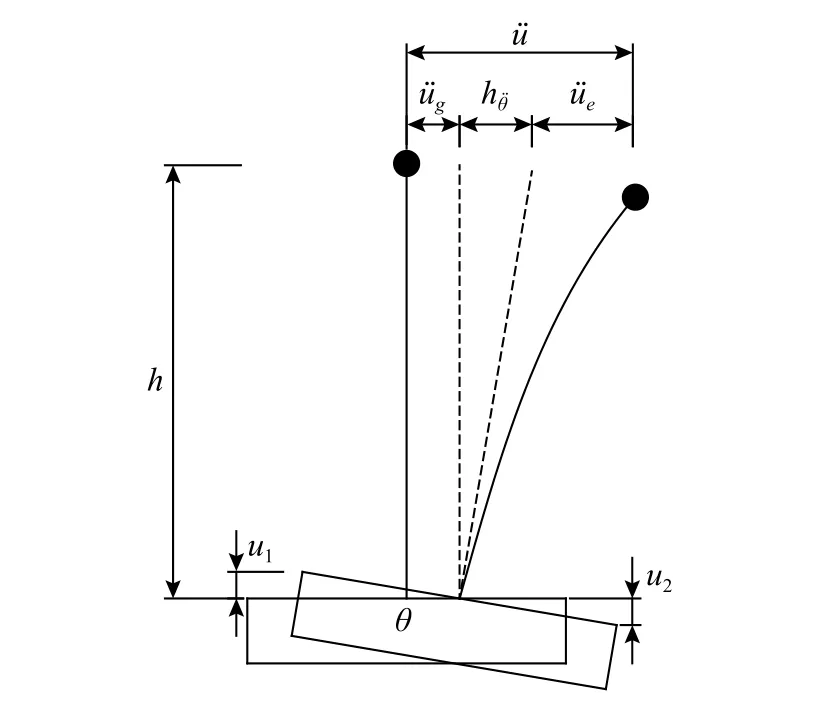
图12 加速度分量Fig. 12 The components of acceleration

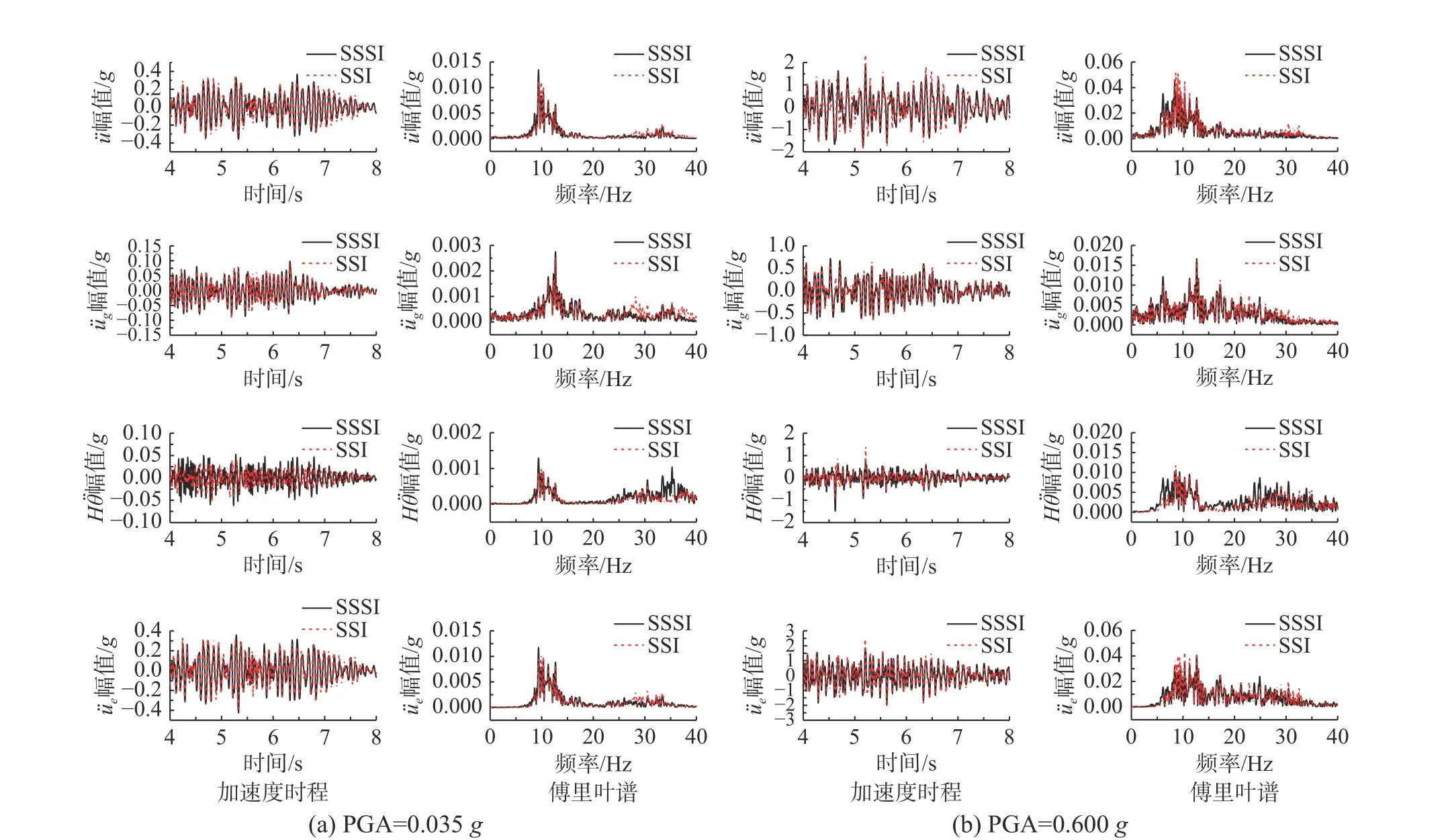
图13 Far-sfern 地震波下结构顶端加速度时程及傅里叶谱Fig. 13 Acceleration time history and Fourier spectrum of the top of frame structure under wave far-sfern
为进一步分析SSSI 体系变形分量的增加效果,令re=βu¨e1/βu¨e2表示SSSI 和SSI 体系中结构顶端变形加速度分量放大系数的比值。表2 为各工况下re的计算结果。由于地下空间结构的局部场地效应影响,re的值可能大于1 也可能小于1,地下空间结构对增强地上结构反应的趋势具有不确定性。6 条输入波6 个输入加速度幅值下,re的值最大可达1.267,最小为0.669。由于未来地震波的不确定性,为保证实际工程结构的抗震安全性,应考虑地下空间结构对邻近结构的影响。

表2 结构顶端变形加速度放大系数比值reTable 2 Ratio of deformation component of acceleration amplification factor at the top of structure re
4 结论
为研究地下空间结构-土-地上结构动力相互作用及其地震反应,以相互邻近的大型地下空间结构和地上框架结构为原型,按照几何相似比为1∶30 进行了实验模型设计和制作,根据实验结果可得出以下结论:
(1) SSSI 体系的动力特性受地下空间结构影响,实验中SSSI 体系的地上结构频率和场地基频均小于SSI 体系,即地下空间结构影响邻近场地的动力特性,进而影响邻近结构的动力特性。
(2) 输入地震波的频谱特性显著影响结构的地震反应,当输入波的卓越频率远大于或小于结构的基频,体系的放大系数较小,而当卓越频率与结构的频率接近时,动力放大系数较大,这一点对SSSI 和SSI 是相同的,且加速度放大系数随输入地震波峰值的增加而降低。
(3) 在SSSI 体系的箱基存在更明显的运动相互作用而导致SSSI 体系的箱基摇摆运动显著大于SSI 体系。随着输入地震波峰值的增加,SSSI 体系的箱基摇摆运动增加幅度更大。SSSI 实验和SSI 实验的箱基摇摆分量与平动分量之比Hθ¨/u¨g在PGA=0.9g时分别达到了2.174 和1.763。
(4) 箱基的平动加速度、摇摆加速度和结构变形加速度分量的峰值并不同步。SSSI 体系箱基摇摆分量增大可能导致上部结构总加速度和变形分量增大。SSSI 体系的结构变形反应最大可达到SSI 体系变形反应的1.267 倍。由于未来地震输入的不确定性,应考虑地下空间结构对邻近地上结构的影响,以提高上部结构的抗震安全性。
——评《多中心城市空间结构:概念、案例与优化策略》

