正常固结非饱和黏性土的三剪弹塑性本构模型
胡小荣,蔡晓锋,李春博,章志荣,瞿 鹏
(南昌大学建筑工程学院,南昌 330031)
Alonso 等[1]所提出的巴塞罗那模型(BBM)为非饱和土本构模型的研究提供了一个完整的理论框架,其后Wheeler 等[2],Vaunat 等[3]在先后在其基础上做了修正。目前,研究者们大多是基于p-q平面上的临界状态框架建立起适用于非饱和土的本构模型[4−6]。其中,破坏应力比M=q/p是非常关键的参数,一般是通过土的强度准则来确定。Mohr-Coulomb 强度准则在非饱和土中的运用非常广泛,但该准则没有考虑中间主应力的影响,现有真三轴试验表明,非饱和土的力学特性很大程度上取决于中间主应力[7]。卢肇钧等[8]、沈珠江[9]所提出的准则也存在相同问题。张常光等[10]基于双剪统一强度理论提出了非饱和土的双剪统一强度准则,该准则虽考虑了中间主应力的影响,但存在双重破坏角现象[11]。Sun 等[12−13]、姚仰平等[14]基于SMP 准则研究了非饱和土的本构模型,其所采用的SMP 准则能考虑中间主应力的影响,但与双剪统一准则相比,统一性方面则略显不足。而三剪统一强度准则[15− 16]既保留了双剪统一强度准则的优势,还能反映土体强度的中间主应力效应、拉压效应和区间效应。陈昊等[17]基于非饱和土的力学特性和三剪强度准则,将Bishop单应力变量理论与Fredlund 双应力变量理论与三剪强度准则相结合,提出了单应力变量和双应力变量下非饱和土的三剪强度准则,并对其做了特征分析和试验验证,证明了其所提准则的合理性。胡小荣等[18]在非饱和土三剪强度准则的基础上采用等量代换法和坐标平移法推导出四个可以反映土体有效黏聚力、应力角和基质吸力影响的三剪破坏应力比。
为此,本文针对正常固结非饱和黏性土本构模型做了以下研究:
1)基于临界状态非饱和土力学框架,把破坏应力比替换成能反映土体饱和度影响的屈服应力和三剪破坏应力比,建立单应力变量和双应力变量下采用等量代换法和坐标平移法的非饱和土三剪屈服函数。据此,建立了4 种不同的非饱和土三剪弹塑性本构模型。
2)确定南昌非饱和黏性土的模型试验参数,并进行相应的常规三轴试验,以验证所提4 种本构模型的正确性。
3)对南昌非饱和黏性土做了真三轴数值模拟,来对比分析不同中间主应力影响系数b和基质吸力s对所提4 种本构模型的影响。
1 正常固结非饱和黏性土三剪弹塑性本构模型

1)单应力变量及双应力变量下采用等量代换法时的屈服函数为:


将式(13)代入式(11)得矩阵形式表示的弹塑性本构关系式为:
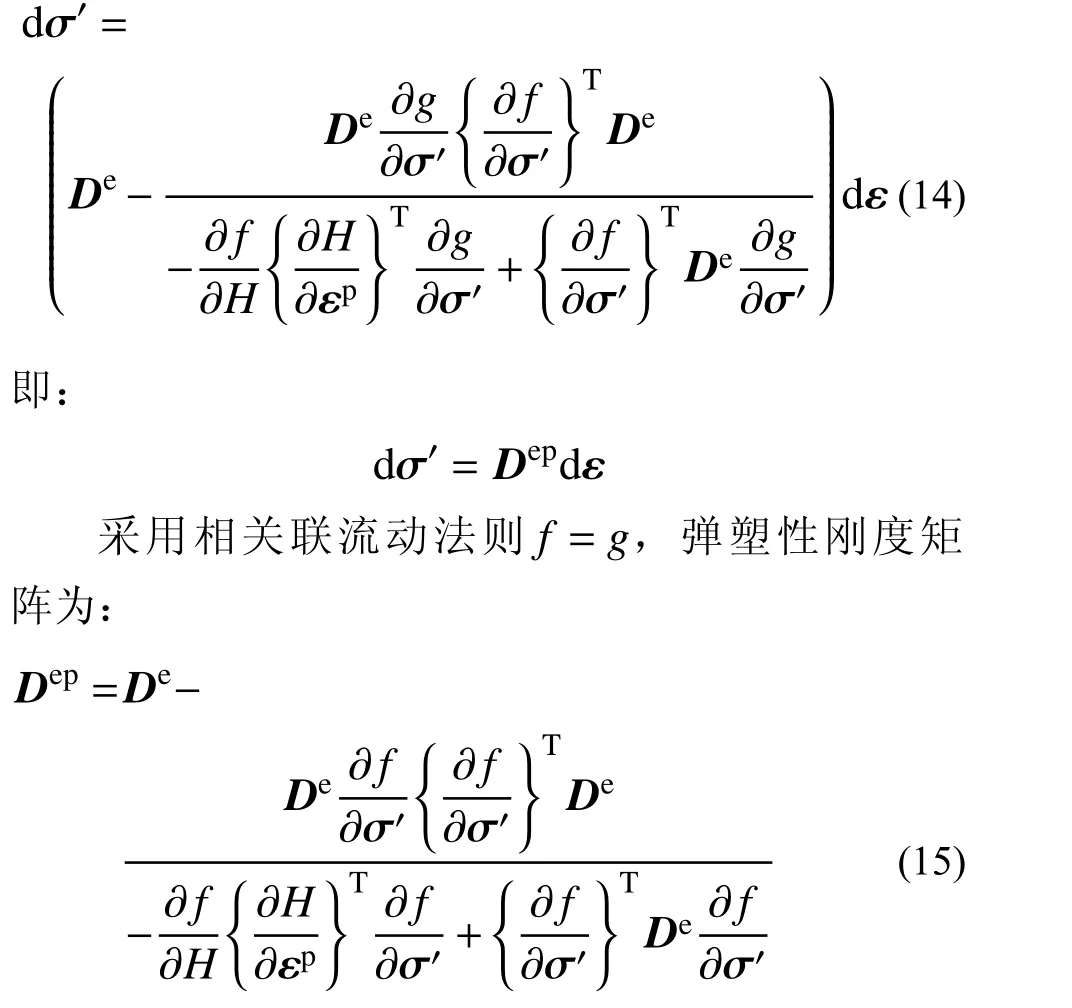
2 模型参数确定及试验验证
为验证本文所提的四种非饱和土本构模型,采用南昌非饱和黏性土为试验对象。南昌非饱和黏性土的基本物理参数为:土体比重Gs=2.75,液限wL=31.5%,塑限wP=20.3%,塑性指数IP=11.2%,最大干密度ρ=1.88 g/cm3,最优含水率w=15.4%。
2.1 模型参数确定
1)有效黏聚力、有效内摩擦角和吸力角的确定。类似于饱和土的直剪试验与三轴试验强度指标较为接近,采用非饱和土直剪仪对非饱和土进行直剪试验,其强度指标与非饱和土三轴试验也具有较好的一致性[20−22]。本文采用YS-SUDS-1 非饱和土应变控制式直剪仪,通过制作基质吸力s=0 kPa、100 kPa、200 kPa、300 kPa、400 kPa 的试样,在法向净压力σ′=100 kPa、200 kPa、300 kPa、400 kPa 条件下分别做了相应的直剪试验,得出对应的抗剪强度,并分别在法向净应力与抗剪强度的坐标系、基质吸力和总黏聚力截距的坐标系中进行线性拟合,如图1和图2 所示,图1 中基质吸力为0 kPa、100 kPa、200 kPa、300 kPa 和400 kPa时拟合优度分别为:0.99、0.97、0.98、0.98 和0.96。进而得到模型所需参数:有效黏聚力c′=27.81 kPa、有效内摩擦角φ′=27.47◦以及吸力角φb=24.7◦。

图1 法向净应力和抗剪强度拟合结果Fig. 1 Relationships between normal stress and shear strength

图2 基质吸力与总黏聚力截距的关系拟合结果Fig. 2 Fitted curve of matrix suction and total cohesion intercept
2)压缩指数λ(s)及回弹指数κ(s)确定。将土样在不同基质吸力s=0 kPa、100 kPa、200 kPa、300 kPa、400 kPa 条件下进行压缩回弹试验,得出试验数据,在e−lnp′关系中按不同s进行线性回归处理得到对应的λ(s)和κ(s)。如表1 所示。

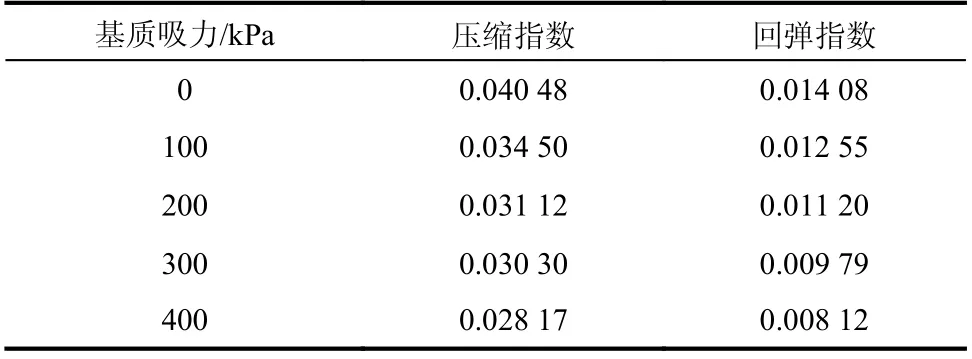
表1 不同基质吸力下的非饱和土压缩指数及回弹指数Table 1 Compressive index and swelling index of unsaturated soils under different matrix suctions
λ(s)回归采用如下方程确定[19]:
s−κ(s)
试验研究表明,满足如下线性关系:
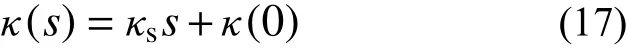
式中,κs是反映κ(s)随着基质吸力s的变化而变化的参数。得到回归参数κ(0)=0.014 08和κs=−1.47×105,模型参数拟合见图3(b)。其拟合优度均大于0.95。
西双说这还不是什么问题,大不了这三万块钱我不要了,可是,假如我们真的又成为夫妻,你说我是应该希望她好起来还是希望她好不起来?万一真的出现奇迹,万一她的病治好了,死不了了,两个人一起面对婚后的漫长生活,怎么办?继续疙疙瘩瘩凑和着过?肯定不行。还得离!那么,不希望她好起来?希望她结了婚就马上死掉?那还是一个正常人的想法吗?那我就丧尽天良了。
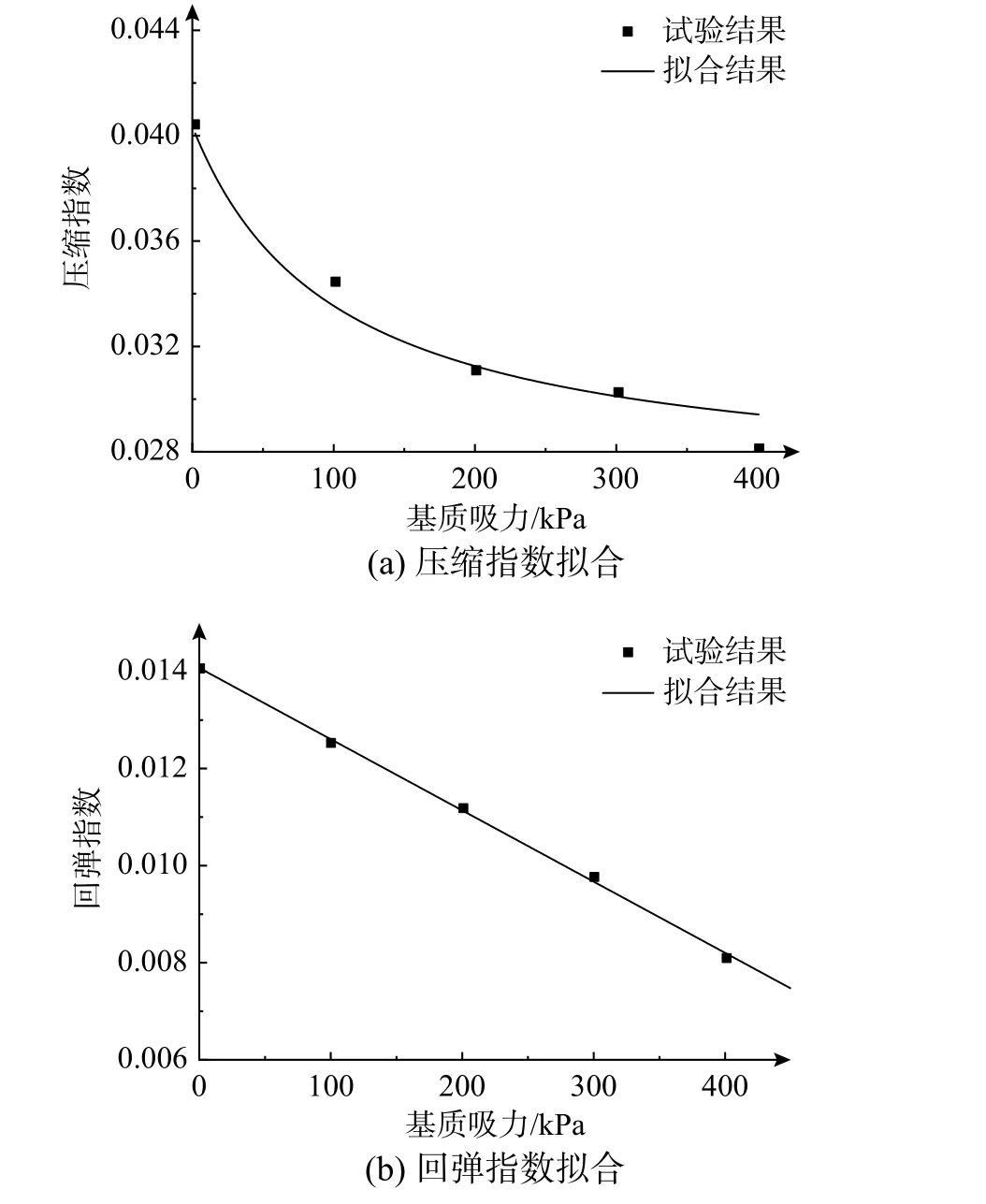
图3 模型参数的拟合结果Fig. 3 Fitted results of model parameters
3)单应力变量法参数χ的确定。χ按文献[23]提出的如下方法确定:
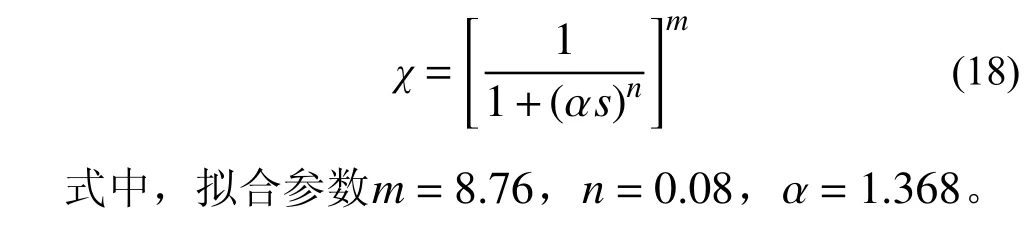
2.2 模型试验验证
对净围压为100 kPa、200 kPa、300 kPa 及基质吸力s为0 kPa、20 kPa、50 kPa、80 kPa 条件下进行非饱和黏性土三轴固结排水试验(Consolidation Drainage,CD),并对比了坐标平移法与等量代换法下三轴试验的模拟值,分析非饱和土在三轴应力状态下的应力特征。限于篇幅且结果均类似,故只列出净围压分别为100 kPa、200 kPa及基质吸力分别为20 kPa、50 kPa 下的单应力变量法和双应力变量法分别模拟土体剪应力q与轴向应变ε1、体应变εv与轴向应变ε1的关系。如图4 和图5 所示。

图4 剪应力与轴向应变关系对比Fig. 4 Comparisons of q-ε1 relationship
图4 表明,4 种模型的剪应力与轴向应变关系曲线趋势大致相同,s不变时,采用单应力变量法和双应力变量法时剪应力与净围压成正比;净围压不变时,两种方法模拟结果曲线的剪应力与基质吸力成正比。其中,采用单应力变量法模拟相对于采用双应力变量法模拟结果曲线偏小,双应力变量法模拟结果更接近试验结果,其原因是单应力变量法处理方式较为简单,并不能像双应力变量法较全面反映非饱和土的力学特性。采用等量代换法相比于坐标平移法模拟结果曲线要略大一些,采用双应力变量法下坐标平移法的模拟结果曲线相较于其他模拟结果曲线更为接近试验结果。
图5 表明,4 种模型的体应变与轴向应变关系曲线趋势大致相同,s不变时,采用单应力变量法和双应力变量法时的围压与εv成正比;围压不变时,两种方法模拟结果曲线的εv与s成正比。其中,采用单应力变量法模拟相对于采用双应力变量法模拟结果曲线偏小,双应力变量法模拟结果更接近试验结果,采用等量代换法相比于坐标平移法模拟结果曲线要略大一些,采用双应力变量法下坐标平移法的模拟结果曲线相较于其他模拟结果曲线更为接近试验结果。
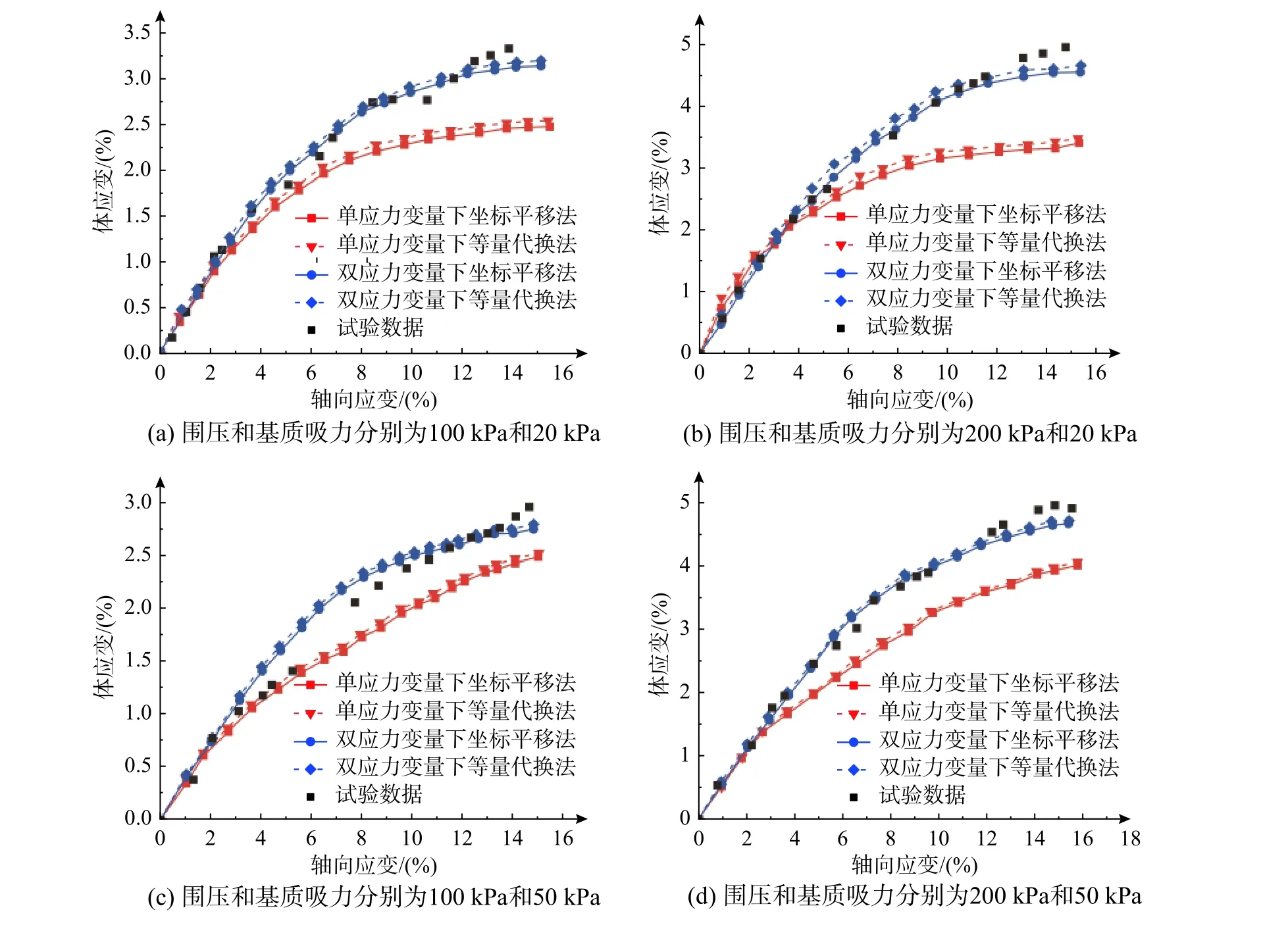
图5 轴向应变与体应变对比Fig. 5 Comparisons of ε1-εv relationship
3 真三轴模拟及影响因素分析
在真三轴压缩条件下,研究南昌非饱和黏性土的力学特性,除了可进行真三轴试验外,将被常规三轴试验验证了的4 种本构模型应用于真三轴数值模拟及其影响因素分析也是可行的。

3.1 中间主应力影响系数b 对4 种模型的影响
在固结排水条件下,σ′2=200 kPa、σ′3=100 kPa、s=0 kPa、50 kPa、80 kPa 和b=0、0.5、1 时对比研究了不同b值对4 种模型的q-ε1和εv-ε1曲线影响。限于篇幅且对比结果均类似,故只列出s=50 kPa 的情况。图6、图7 分别为单应力变量法、双应力变量法下等量代换法和坐标平移法的真三轴数值模拟对比结果。
图6 和图7 表明,单应力变量法和双应力变量法下采用等量代换法和坐标平移法的模拟结果曲线均比较接近,其趋势大致相同,尤其是qε1对比曲线非常接近。相同轴向应变ε1情况下,采用等量代换法相比于坐标平移法其剪应力和体应变均偏大。当s和ε1不变时,q、εv均与b值成正比。
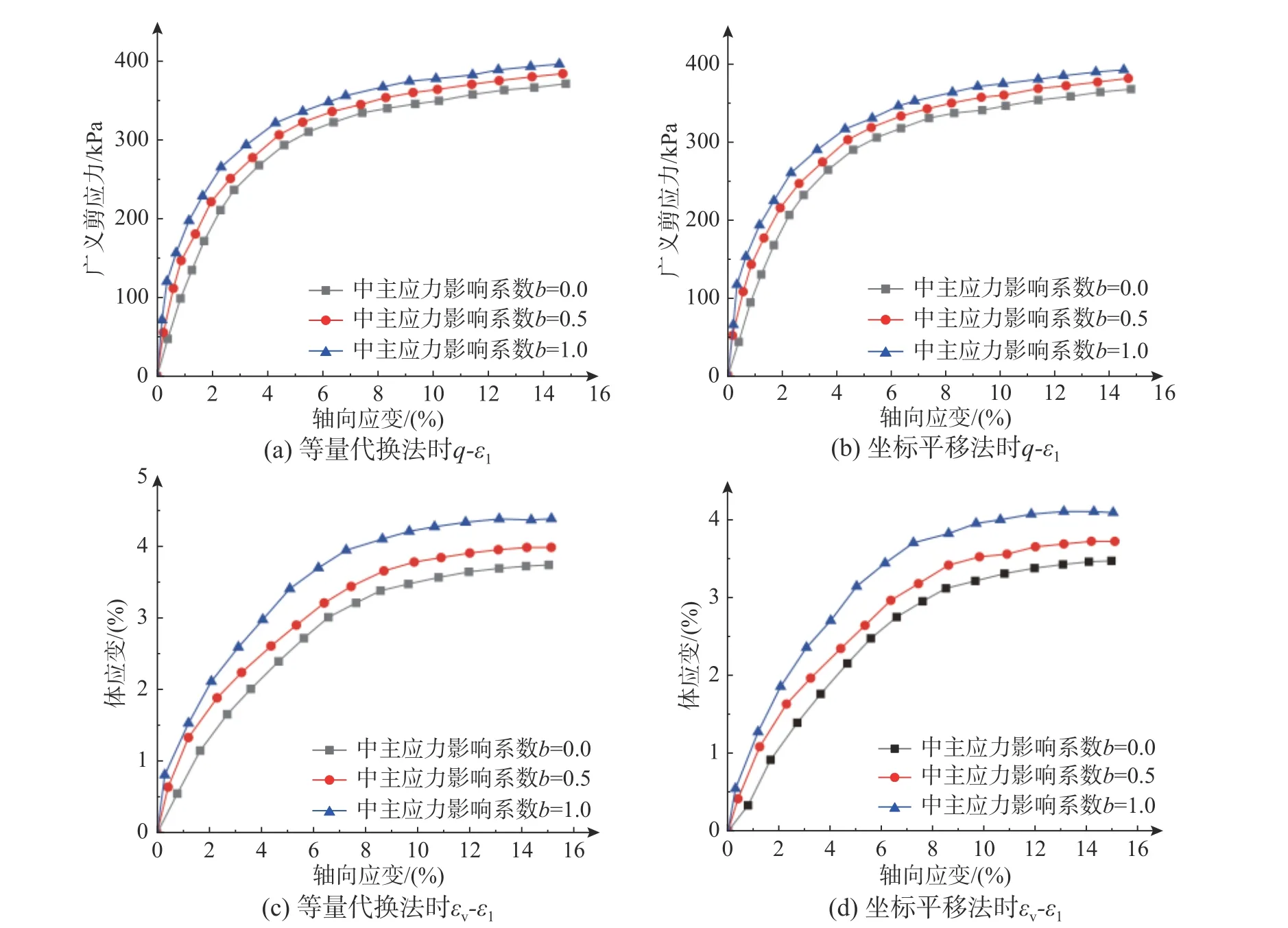
图6 单应力变量法下基质吸力为50 kPa 时中间主应力影响曲线图Fig. 6 Influence curves of intermediate principal stress when matrix suction is 50 kPa by single-stress variable method
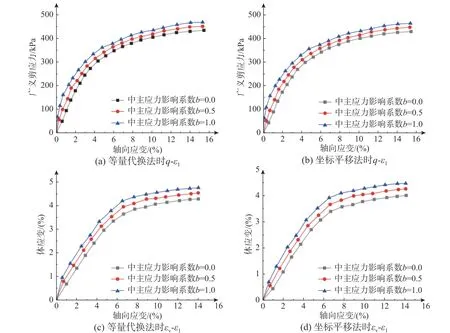
图7 双应力变量法下基质吸力为50 kPa 时中间主应力影响曲线图Fig. 7 Influence curves of intermediate principal stress when matrix suction is 50 kPa by double-stress variable method
3.2 基质吸力s 对4 种模型的影响
在固结排水条件下,b=0、0.25、0.5、0.75、1、 σ′2=200 kPa、 σ′3=100 kPa 和s=0 kPa、50 kPa、80 kPa 对单应力变量和双应力变量下采用等量代换法和坐标平移法的4 个模型分别做了真三轴数值试验。限于篇幅且结果均类似,故只列出b=0.5时,s=0 kPa、50 kPa 下的q-ε1和εv-ε1的对比结果。如图8 所示。
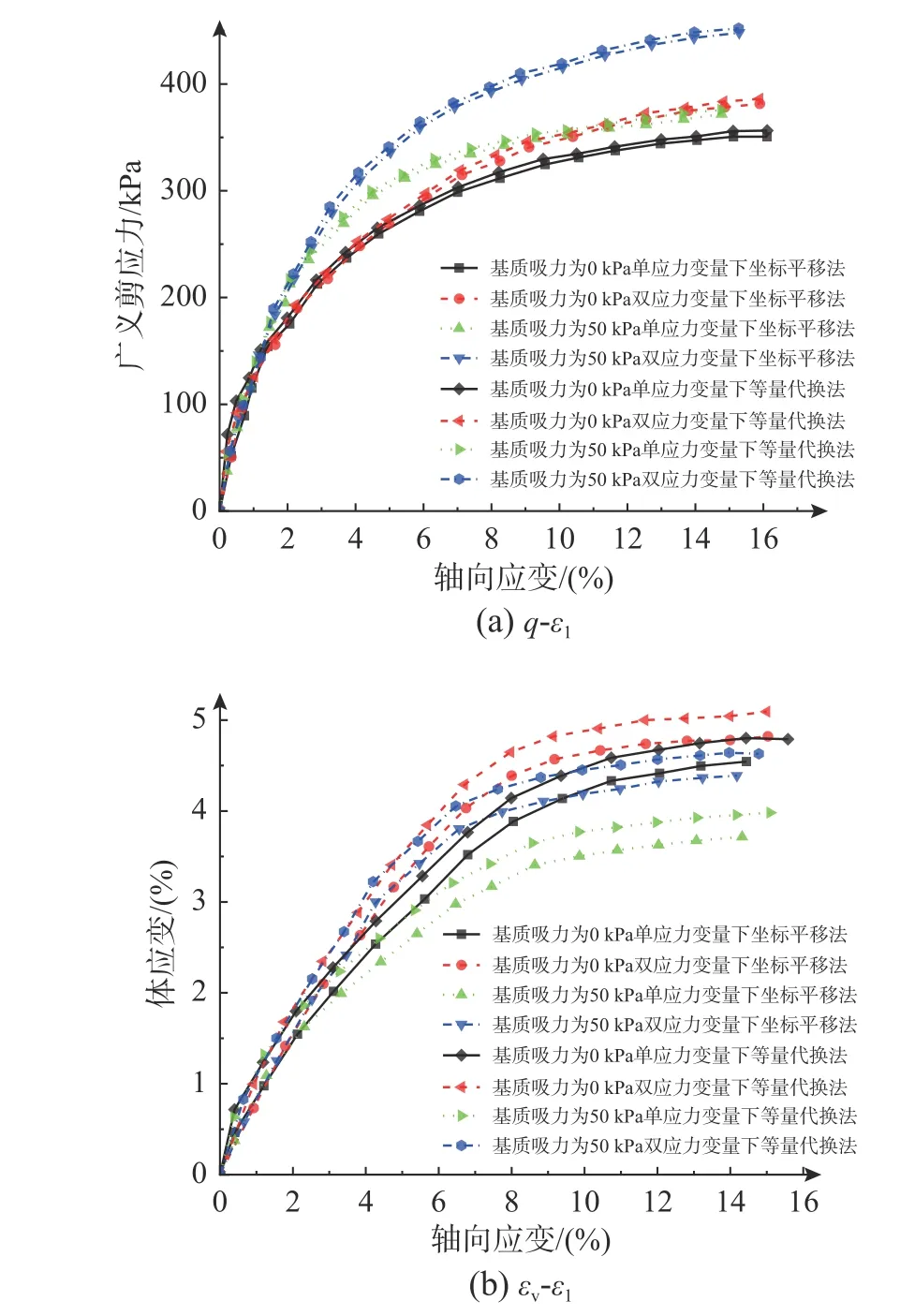
图8 不同基质吸力下4 种模型的真三轴模拟结果Fig. 8 Comparisons of true triaxial simulated results of four constitutive models with different matrix suctions
图8 表明,4 种模型的q-ε1和εv-ε1真三轴数值结果曲线变化趋势均大致相同。其中,图8(a)表明,当b值不变时,4 种模型的q均与s成正比关系。相同情况下,采用双应力变量下坐标平移法模型的广义剪应力较其他模型偏大。图8(b)表明,当b值不变时,4 种模型的εv与ε1均成正比关系。ε1和b值不变时,采用双应力变量法相对于单应力变量法的εv偏大,采用等量代换法相对于坐标平移法的εv也偏大,而s越大,εv反而相对偏小。
4 结论
在临界状态土力学框架下,采用非饱和土的三剪强度准则建立了4 种不同正常固结非饱和黏性土的三剪弹塑性本构模型。针对南昌非饱和黏性土确定了试验参数、做了常规三轴试验及真三轴数值模拟对比分析。结论如下:
(1)所建立的4 种非饱和黏性土弹塑性本构模型考虑了中间主应力影响系数b,能够很好的反映中间主应力对非饱和黏性土的影响。此外,还能够反映非饱和黏性土的中间主应力效应、拉压差效应和应力区间效应。
(2)以南昌非饱和黏性土为研究对象进行非饱和黏性土的土性参数确定及其常规三轴试验,常规三轴试验结果表明,4 种非饱和黏性土本构模型均能较好模拟土体的应力-应变关系,还可以反映非饱和黏性土的应变硬化特性。采用双应力变量法相对单应力变量法更接近真实试验结果,而采用坐标平移法相对等量代换法更接近真实试验结果。在双应力变量法下采用坐标平移法相对其他模型更加接近真实试验结果。
(3)真三轴数值模拟对比结果表明,随着中间主应力影响系数增大,4 种本构模型的广义剪应力和体应变也会随之增大;其他条件不变时,基质吸力越大,广义剪应力也随之变大;采用双应力变量法相对单应力变量法所得广义剪应力和体应变也偏大。
附录:

式中:L为Lame 常数;G为剪切模量。

上式各元素分别为:



