圆钢管混凝土在自由扭转作用下扭矩-应变理论模型
赵均海,高伟琪,樊军超
(长安大学建筑工程学院,西安 710061)
钢管混凝土在我国已有近60 年的应用历史,与普通钢筋混凝土材料相比,具有更高的承载能力、塑性、韧性和抗震性能[1]。结合施工方便、可修复强等优点,常被用于重载、大跨、高耸等结构中,带来了出色的社会和经济效益[2−3]。钢管混凝土在实际受力中常处于压、弯、剪、扭及耦合的复杂受力状况下,在复杂受力下结构更容易发生破坏[4]。随着建筑体型和结构的日趋复杂,钢管混凝土的扭转作用也受到越来越多学者的关注[5−12]。受扭性能作为钢管混凝土的基本力学性能,需对钢管混凝土的受扭性能进行理论分析,从而为钢管混凝土在复杂作用下的研究和设计打下基础。
目前,国内外学者利用不同的方法对钢管混凝土受扭问题做了一定的研究,韩林海等[13−14]通过对在自由扭转作用下的圆钢管混凝土进行试验研究和数值模拟,阐述了试验现象,定义了抗扭承载能力,基于回归分析提出了钢管混凝土抗扭承载能力简化计算公式。然而,由于试验数据较少,采用回归分析研究钢管混凝土受扭承载力会带来了未知的误差。金伟良等[15]通过对薄壁离心钢管混凝土进行研究,提出混凝土开裂方式。Lee 等[16]以空间桁架模型为基础,提出了在轴压力作用下圆钢管混凝土抗扭承载力计算公式。聂建国等[4]利用“分层筒”模型,编制了圆钢管混凝土在轴力-扭矩复合作用下非线性迭代求解程序,计算复杂。王宇航等[17]通过对圆钢管混凝土在纯扭和压扭作用下的拟静力试验研究,基于回归方法,提出了适用于工程设计的承载力简化公式,具有一定的应用范围。Ding 等[18]基于数值模拟对圆钢管混凝土在纯扭作用下的扭矩-应变曲线做了全过程分析,表明核心混凝土的延性得到很大程度的提高,据此提出了圆钢管混凝土抗扭承载力计算公式。以上对于圆钢管混凝土的扭转问题的研究中,其扭矩-应变关系曲线大多采用试验、模拟和迭代的方式来确定,缺乏一种实用经济、简单方便的函数确定方法。其抗扭承载力大多采用回归分析,缺乏一种适用范围较广、概念明确的计算方法。
本文在文献研究的基础上,将圆钢管混凝土在自由扭转条件下的全过程分为三个阶段。在理论基础中推导出基于统一强度理论的钢材和混凝土的抗剪强度,结合在扭转作用下切应变与正应变之间的关系,通过对各个阶段的钢管和混凝土的受力状态、协调变形和相互作用进行分析,钢材采用理想弹塑性本构关系,混凝土考虑了开裂的软化效应且由于受力状态的不同采用不同的本构关系,提出了圆钢管混凝土在自由扭转下的扭矩-应变理论模型和抗扭承载力计算公式。通过试验结果对比验证了模型的正确性,然后,利用本文中的模型分析了混凝土强度、钢材强度、含钢率和钢管直径对扭矩-应变关系曲线的影响,据此提出工程应用中的建议。
1 理论基础
1.1 统一强度理论

1.2 钢材和混凝土的抗剪强度
抗剪强度决定了钢材和混凝土何时屈服和开裂。在圆钢管混凝土研究中常采用混凝土圆柱体抗压强度[3],圆柱体抗压强度也该用于圆钢管混凝土在扭转问题下的研究,从而需要得到混凝土抗剪强度与圆柱体抗压强度之间的关系。除此之外,已有的规范和研究中已经给出的强度转换方法大多只适用于某一类材料,未有一种适用范围广、计算简便的强度转换公式。
已有的规范和研究中,钢材常采用钢结构设计标准[20]中规定得钢材的抗剪强度与屈服强度之间的关系:

式中:τsmax为钢材抗剪强度;fy为钢材屈服强度。
目前国内外测量混凝土抗剪强度的方法差异较大,主要有矩形短梁直接剪切试验、单剪面Z 形试件试验、梁四点受力试验、薄壁圆筒受扭试验和二轴拉压试验。文献[21]指出前两种试验中试件剪切面上剪应力分布不均匀且存在在较大的正应力,给出的混凝土抗剪强度值偏高;后三种试验中试件剪切面上的剪应力分布均匀,正应力较少,三种方法的抗剪强度值较为接近。由于混凝土抗剪强度实验数据的离散性,文献[21]在误差允许的范围内对以梁四点受力试验数据进行回归分析得到混凝土抗剪强度:

同理,如式(9)所示,可得到混凝土抗剪强度与立方体抗压强度之间的关系。



表1 钢材抗剪强度比较Table 1 Comparison of steel shear strength
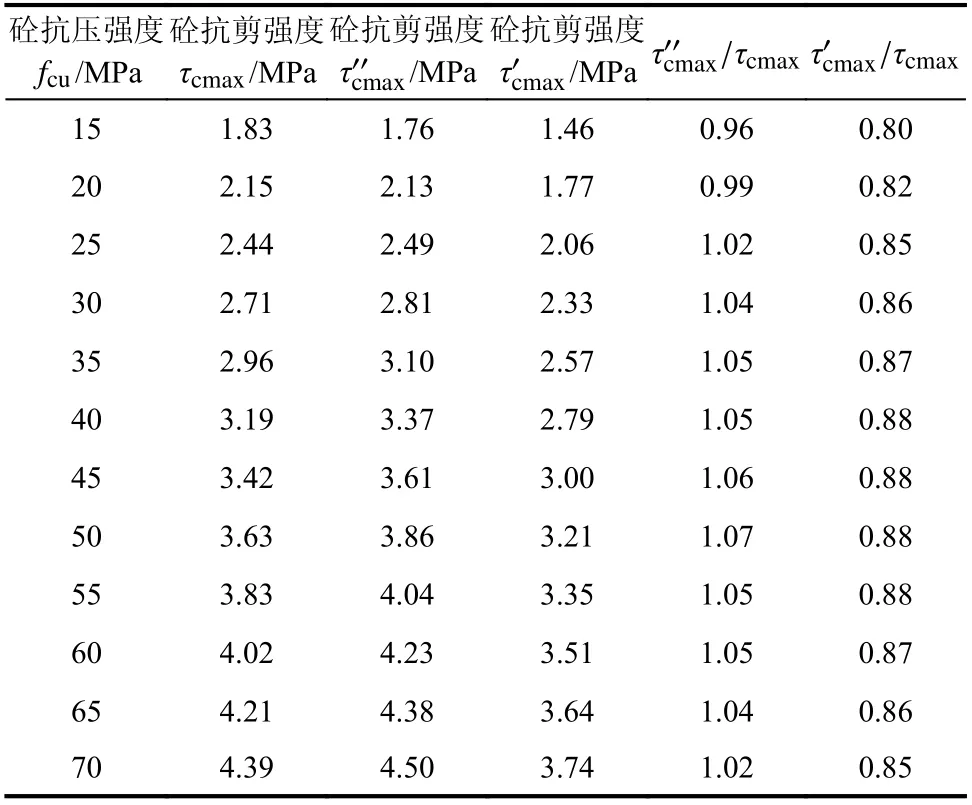
表2 混凝土抗剪强度比较Table 2 Comparison of concrete shear strength
1.3 在弹性阶段切应变与正应变的关系


图1 扭转作用下单元体的应力状态Fig. 1 Stress state of the element under torsion


图2 扭转作用下切应变与正应变的关系Fig. 2 Relationship between shear strain and normal strain under torsion

如表3 所示,利用式(15)计算得出钢材的正应变后代入式(16)得到单元体的正应力,纯剪切状态下的切应力与转换为二向应力状态的拉、压正应力值的比值为1,验证了式(15)的正确性。同理,如表4 所示,验证了混凝土也可利用式(15)来计算切应变与正应变之间的关系。
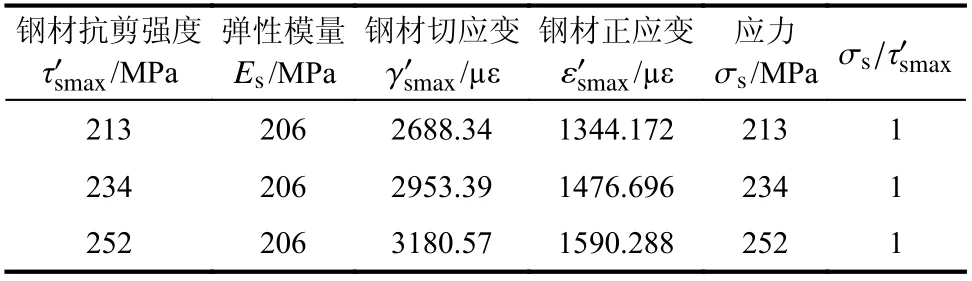
表3 钢材切应变与正应变的关系Table 3 Relationship between shear strain and normal strain of steel
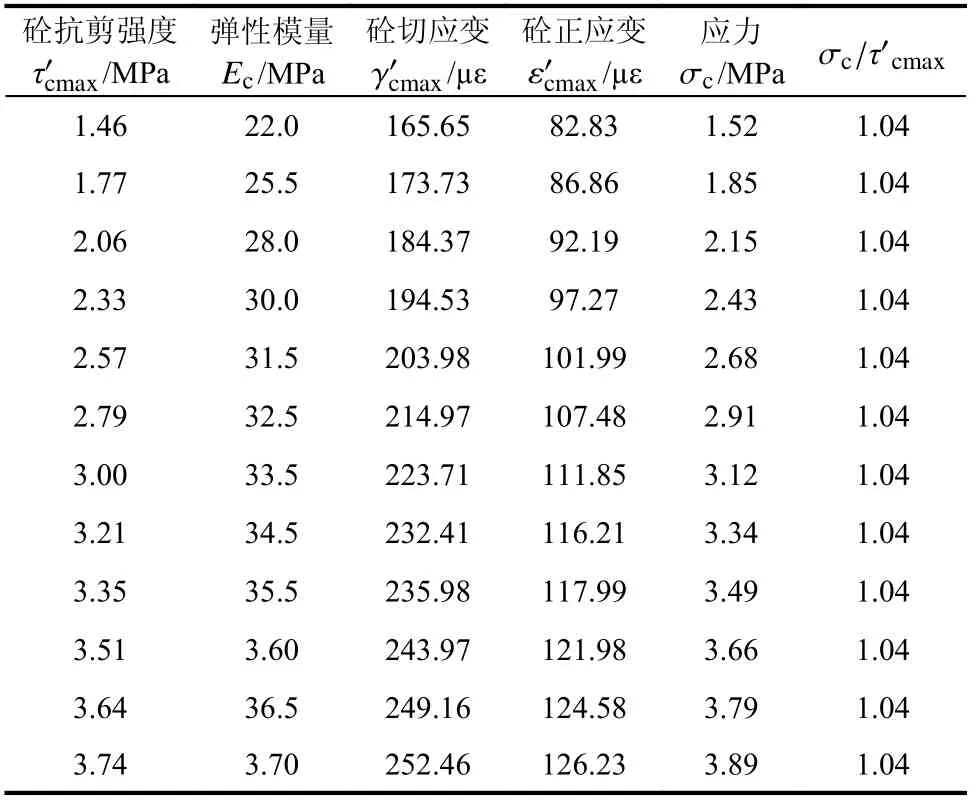
表4 混凝土切应变与正应变的关系Table 4 Relationship between shear strain and normal strain of concrete
2 理论模型
圆钢管混凝土在自由扭转作用下,截面在试验过程中服从平截面假定,核心混凝土表面存在不等量细微裂缝,外钢管分布着近45°的滑移线,钢管内壁和核心混凝土没有划痕,钢管和混凝土粘结良好、变形协调[13]。根据试验现象,将圆钢管扭转全过程分为混凝土开裂前、钢管屈服前和钢管屈服后三个阶段。由于圆钢管混凝土在自由扭转作用下有良好的塑性性能,扭矩-应变曲线逐渐趋于平缓,扭矩增幅很小[13−14]。因此,钢管的本构关系采用理想的弹塑性本构关系。而混凝土在各个阶段的受力状态是不同的,表现出的力学性质差异较大,因此混凝土的本构关系在各个阶段是变化的。
2.1 混凝土开裂前
混凝土在开裂前,混凝土应力水平较低,内部的微裂缝并未得到发展,因此采用线弹性本构关系。由于钢管混凝土在扭转作用下变形协调,其实测切应变为钢管外边缘的切应变,因此需要得到钢管外边缘的切应变与各处切应变之间的关系。如图3 所示,根据材料力学相关知识,钢管混凝土的切应变γ 与相对扭转角θ 的关系为:


图3 切应变和扭转角之间的关系Fig. 3 Relationship between shear strain and torsion angle
由式(17)积分可得单位长度的钢管混凝土切应变γ 与相对扭转角θ 和相应半径ρ 之间成正比。钢管混凝土在自由扭转作用下截面上相对扭转角相等,因此切应变在截面上沿半径是线性变化的。钢管混凝土截面尺寸如图4 所示,则外钢管外边缘的切应变γ 与混凝土外边缘的切应变γc的比值为:

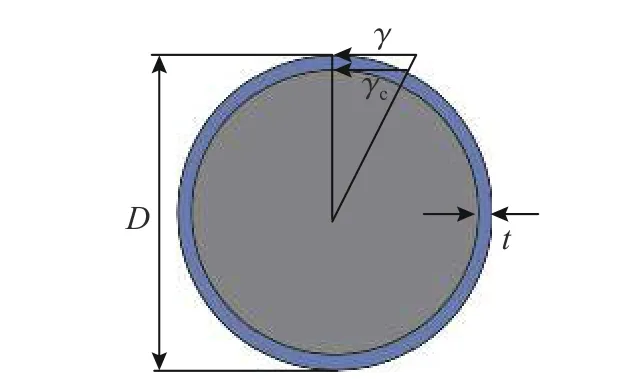
图4 圆钢管混凝土截面尺寸Fig. 4 Section dimensions of concrete filled circular steel tube
钢管和混凝土处于弹性阶段时,根据材料力学由式(19)和式(20)可以求得钢管和混凝土的极惯性矩Iρs、Iρc,取 α3为内外径的比值α3=(D−2t)/D。

在混凝土开裂前,钢管和混凝土独立工作,单独承受各自的外扭矩[13]。因此,根据式(21)和式(22)可求得此时钢管和混凝土各自承受的外扭矩Ts、Tc,由式(23)可求得钢管混凝土承受的外扭矩Tu。
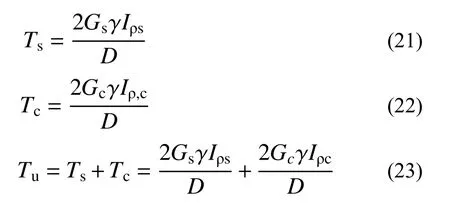

2.2 钢管屈服前
将在扭矩作用下纯剪切状态的单元体转变为拉、压二向应力状态来进行裂缝分析,由式(15)可知在纯扭矩作用下切应变越大,相应的拉、压正应变越大。混凝土的极限拉应变远小于极限压应变,素混凝土在扭矩作用下达到极限切应变后,在拉应力方向被拉裂,在表面薄弱处出现45°的斜裂缝;在拉应力的作用下,裂缝沿着半径快速向内发展,素混凝土表面裂缝快速变宽,素混凝土迅速丧失承载力显示出脆性破坏[23]。文献[13]表明钢管和核心混凝土粘结良好、变形协调。由于钢材的极限拉应变远大于混凝土的极限拉应变,在钢管和核心混凝土的接触面上有粘结力的存在,核心混凝土表面薄弱处出现裂缝后,核心混凝土将裂缝区域的拉应力传递给钢管,使得核心混凝土和钢管的拉应变协调,从而阻碍了表面裂缝的快速变宽,抑制了裂缝沿半径开裂的速度。如图5(a)所示,核心混凝土可以分为未开裂部分和开裂部分。

图5 混凝土开裂后的钢管混凝土截面Fig. 5 Section of concrete filled steel tube after concrete cracking
由于同一截面上相对扭转角是相同的,因此利用切应变与相应半径成正比的关系通过式(26)可求得未开裂混凝土的半径rnc。混凝土由于表面材料的不均匀,裂缝最开始于薄弱的部分,随着扭转角的持续增加,便会产生大小不等呈45°的裂缝分布在混凝土外边缘。假设混凝土材料表面性质是均匀的,可利用式(15)求得切应变与正应变的关系,通过式(27)求得此时混凝土的拉伸差值,即得到仅供参考的单个裂缝的宽度。

金伟良等[15]通过对薄壁离心钢管混凝土进行研究,表明混凝土开裂后不再继续承担拉应力而是以斜短棱柱体的方式受压。由于钢管和核心混凝土之间粘结力的存在,核心混凝土已产生拉应变并不会消失,而是保持原有的拉应力水平。随着荷载的增加,钢管比核心混凝土能够产生更大的拉应变,然而,核心混凝土的拉应变由于材料性质的限制无法继续产生时,则通过产生45°的裂缝来弥补缺少的拉应变。说明核心混凝土裂缝的产生只是弥补拉应变的不足,核心混凝土和钢管会同步变形,开裂的混凝土并不会对钢管产生膨胀作用。
因此,本文认为开裂部分的混凝土不再承担新增加的拉应力,而是通过粘结力传递给钢管,使得钢管处于拉扭状态;同时,开裂部分的混凝土在压应力方向承担梯形分布新增加的压应力,为方便计算,假设处于单轴受压状态,且以混凝土外边缘的压应变作为该斜柱体横截面的压应变,如图6 所示。由于在同等变形的情况下混凝土的应力与钢材的应力相差较大,本文忽略开裂部分混凝土在压应力方向的贡献,认为开裂部分混凝土将新增加的拉应力和压应力全部传递给钢管,从而使得钢管承担了开裂部分的混凝土传递的不利扭矩T1。
图6 混凝土开裂后受力状态Fig. 6 Stress state of concrete after cracking
如图5(b)所示,外钢管和未开裂部分的混凝土能够继续承担外扭矩,外钢管承担的外扭矩仍通过式(21)进行计算,而未开裂部分的混凝土可利用材料力学知识进行求解,其极惯性矩可通过式(28)进行计算,所承担的外扭矩利用式(29)进行计算。
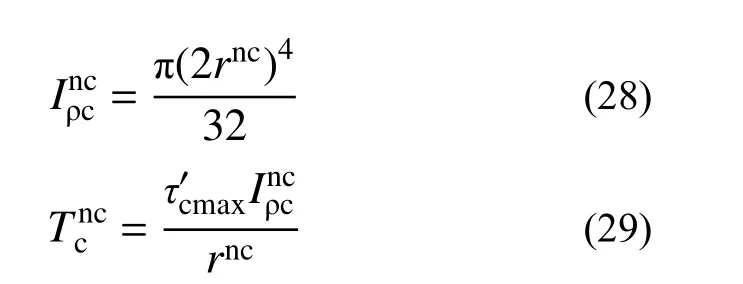
除此之外,由于开裂部分的混凝土保持开裂时的应力水平并没有迅速丧失承载力而表现出塑性性质,从而开裂的混凝土会承担塑性扭矩Tp,根据材料力学可得塑性扭矩如式(30)。

由于核心混凝土的裂纹为垂直于拉应力方向的多条平行裂纹,Vecchio 和Collins[24]所提出的混凝土的本构关系能够很好描述此状态下混凝土受压软化,因此开裂的混凝土采用Vecchio 和Collins[24]受压软化本构关系,如式(31)。此处认为混凝土是非线弹性材料,开裂混凝土在单轴受压下的压应变是在混凝土开裂后的基础上增加的新的压应变 ε1,假设混凝土在钢管边缘屈服前的压应变是处于本构关系曲线上升阶段的,即临界状态时混凝土的压应变小于等于0.002,联立式(7)、式(15)和式(18)得钢管屈服强度应小于528/α3MPa。将新增加的压应变 ε1代入到上述混凝土本构关系式(30)中便可得到此时混凝土所受到的压应力σ1,开裂混凝土给外钢管的附加扭矩T1则可通过式(32)计算。


2.3 钢管屈服后
素混凝土在扭矩作用下开裂后,在拉应力的作用下裂缝迅速贯通,试件在裂缝处断裂,导致内力消失。而核心混凝土只是表面存在不等量的细微裂缝,并未断裂,仍为一个完整的柱体[13]。随着外扭矩的增加,开裂的混凝土需要将增加的拉应力传递给钢管,屈服的钢管在塑性状态时体积不发生改变,若将增加的拉应力传递给开始屈服的钢管时,钢管在压应力方向的横向变形将快速增大。然而,开裂的核心混凝土在压应力方向处于单轴受压状态,能够继续承担压应力,通过钢管和核心混凝土之间的粘结力,核心混凝土在压应力方向阻碍了钢管横向变形的快速增大,一方面防止了钢管产生局部屈曲,另一方面使得钢管能够继续承担核心混凝土传来的拉应力。因此,在钢管屈服后阶段,开裂的核心混凝土承担压应力,钢管承担拉应力,在钢管和混凝土的协同工作下形成了一个有利附加扭矩T2。
由前文分析可知,核心混凝土阻碍了屈服钢管的变形,使得钢管和核心混凝土的变形不同步。如图7(a)所示,屈服的钢管部分在拉应力方向就像是缠绕在核心混凝土上的拉力带,由于变形不同步而对核心混凝土产生围压,拉力带的厚度就是钢管屈服部分的厚度,随着扭转角的增加拉力带的厚度t′也不断增加,直至钢管全截面屈服t′=t。t′可利用切应变与半径之间的正比关系求解,如式(35)。
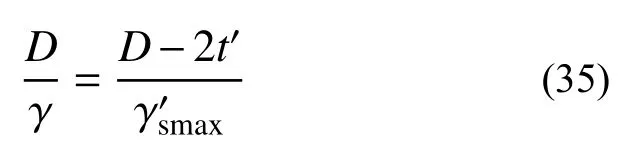
如图7(b)所示,拉力带的截面呈椭圆形状,由于在同等变形的情况下混凝土的应力远小于钢材的应力,从而忽略混凝土传给钢管的拉应力,认为屈服部分的拉应力与钢管的抗剪强度大小相等,为了简化计算,假设围压等于分别以长短边为半径的半圆钢管的围压的平均值。而半圆钢管的围压可通过式(36)计算,将长短边代入式(36)积分后求平均值便可得到拉力带的围压p1,如式(37)。

图7 钢管屈服部分的受力状态Fig. 7 Stress state of the yield part of the steel pipe

式中:p为半圆钢管的围压;r为半圆钢管的半径。
由于钢管是薄壁钢管,本文以钢管最外层达到屈服时作为钢管的全截面塑性扭矩。
随着钢管逐渐产生围压,开裂的混凝土处于围压相等的三轴受压状态。此处认为混凝土是非线弹性材料,因为Ottosen 本构关系与大多数三轴受压混凝土试验结果吻合良好,所以该阶段混凝土的本构关系选择Ottosen 本构关系[25−26]。考虑到混凝土的严重的开裂软化效应,参考Vecchio和Collins[24]所提出的软化混凝土的本构关系,给Ottosen 混凝土本构关系附加一个软化系数。结合变形受力状况和实际工程中的应用,以γc=0.01时对应的βMCFT=0.6作为此时的软化系数。


此时钢管混凝土所承受的外扭矩为钢管最外层屈服时的钢管混凝土外扭矩和新增加的有利扭矩之和:

综上所述,圆钢管混凝土在自由扭转下的扭矩-应变分段式函数理论模型为式(42):

3 模型验证
钢管混凝土在两端翘曲不受到限制的作用下才会发生自由扭转,或者Wang 和Zhao[27]指出受约束扭转作用的构件长细比较大时,由约束扭转所产生的约束剪切应力影响很小,此时也可将此受扭构件看作自由扭转。目前只有文献[13 − 14, 28 − 29]中前人试验结果满足以上要求。
韩林海和钟善桐[13]对4 个不同含钢率和不同长细比圆钢管混凝土试件在自由扭转作用下进行了试验研究,通过伺服拉压式千斤顶在试件两端钢臂上施加载荷,加载值由接电子传感器的电子秤读出,切应变由120°角的应变花量测。
利用式(42)计算结果如图8 所示,本文所提出的扭矩-应变理论模型与试验结果[13]吻合良好,曲线总体走向趋于一致。由于试验装置的限制,试件未处于理想的自由扭转状态下,TCB1-1 和TCB2-1 的长细比较小,造成试件钢管屈服前阶段受到约束扭转效应,从而,使得在该阶段本文模型的外扭矩比试验实测的外扭矩偏小。除此之外,本文忽略开裂部分混凝土在压应力方向的贡献,认为开裂部分混凝土将新增加的拉应力和压应力全部传递给钢管,导致附加扭矩T1比实际值偏大,使得在钢管屈服前阶段本文模型的外扭矩比试验实测的外扭矩也偏小。
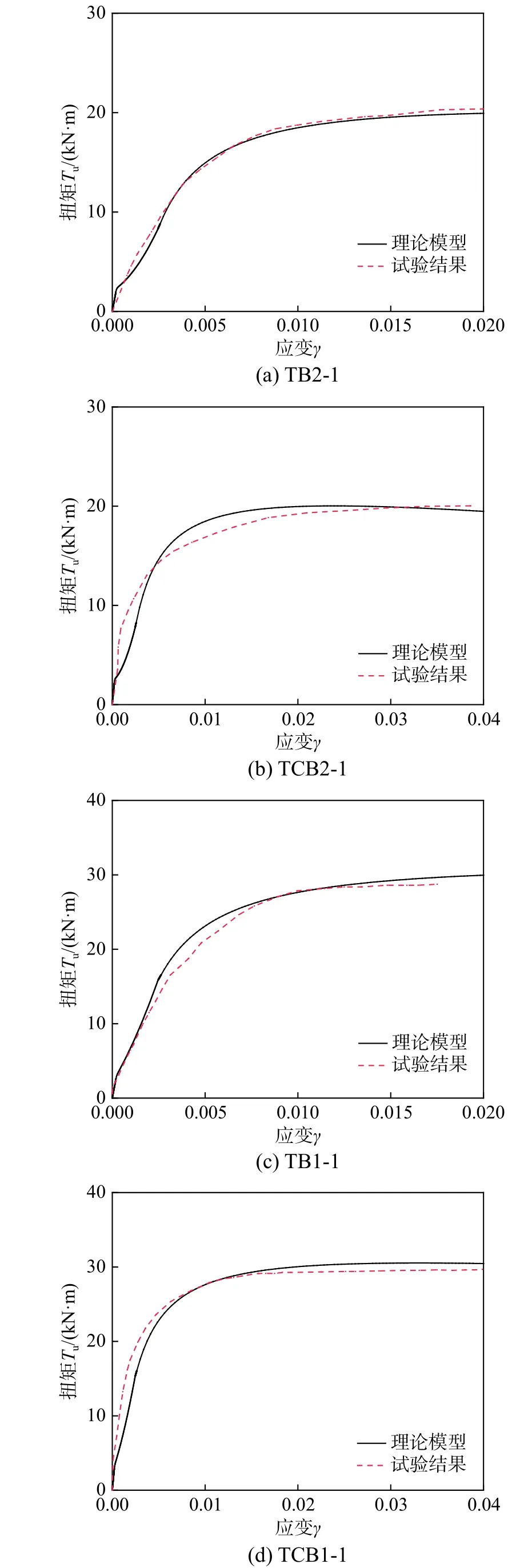
图8 理论模型曲线与试验结果对比Fig. 8 Comparisons between theoretical model curves and test results
韩林海和钟善桐[13]根据试件的变形受力状况和实际工程中的应用,定义试件边缘切应变达到0.01 ε时对应的外扭矩为试件的抗扭承载力,因此基于本文中的理论模型,将γ=0.01代入式(41)可得试件的抗扭承载力计算公式,并将结果列于表5。由表5 可知,由式(41)计算得到的试件的抗扭承载能力与试验结果的平均比值为0.996,标准差为0.0579,证明了本文所提出的抗扭承载力计算方法的正确性;圆钢管混凝土在自由扭转下的抗扭承载力比圆钢管和素混凝土之和增加20.17%~25.07%,增加率与试验结果[13]吻合良好。文献[13]提出的回归计算公式得到的试件抗扭承载能力与试验结果的平均比值为1.032,标准差为0.0500,与本文计算结果进行比较,可知在标准差相似的情况下,本文的误差较小。
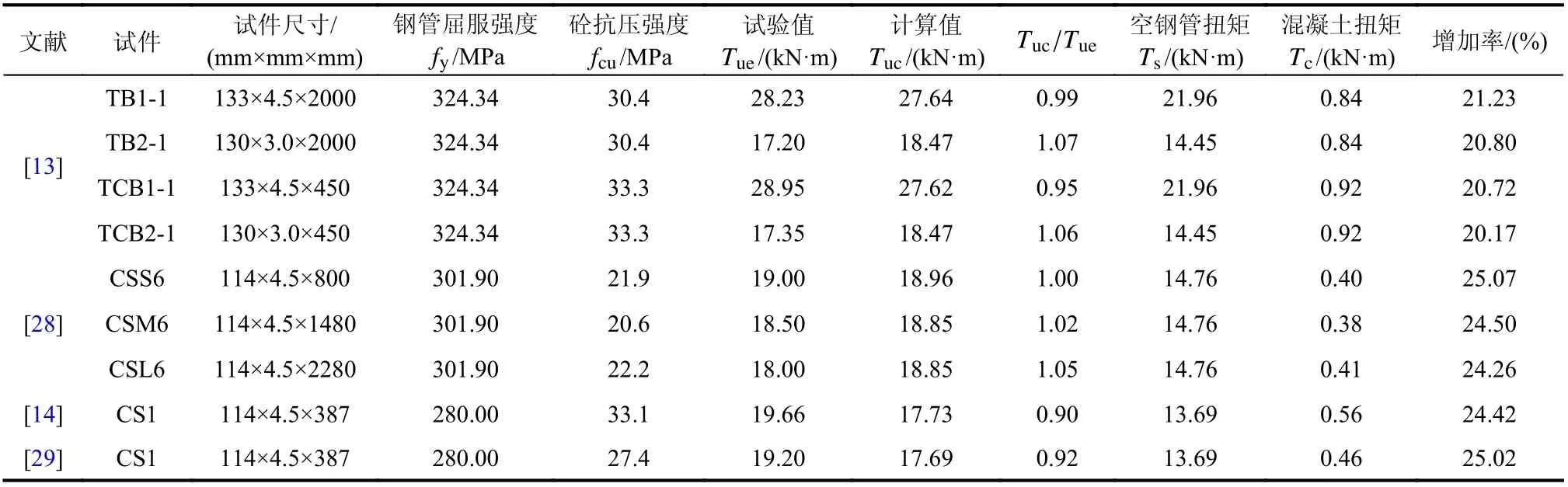
表5 计算结果和试验结果对比Table 5 Comparisons of calculation results and test results
4 参数分析
通过对圆钢管混凝土在自由扭转下的理论分析可知,影响圆钢管混凝土抗扭承载力的因素有混凝土强度、钢材强度、含钢率和钢管直径。因此,利用本文所提出的圆钢管混凝土扭矩-应变理论模型对上述影响因素进行参数分析,据此提出相关设计建议。
4.1 混凝土强度
为说明混凝土强度对扭矩-应变关系曲线带来的影响,本文选取直径为133 mm、厚度为4.5 mm、钢材强度为324.34 MPa 和不同混凝土强度的圆钢管混凝土进行参数分析。由图9(a)可知,随着混凝土强度的增加,试件在混凝土开裂前阶段抗扭刚度提升的不明显,不利的附加扭矩T1却显著增加,从而,使试件在钢管屈服前阶段的外扭矩显著减少。因钢管屈服后混凝土处于三轴受压状态,强度越高的混凝土所提供的有利附加扭矩T2增加得越快,在0.01ε 处试件的抗扭承载力基本相同。由图9(b)可知,随着混凝土强度的增加,增加率却随之减少。
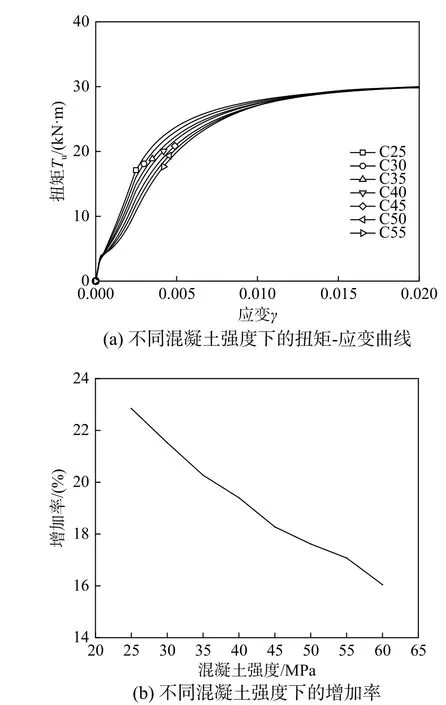
图9 混凝土强度对扭矩-应变关系的影响Fig. 9 Influence of concrete strength on torque-strain relationship
4.2 钢材强度
为说明钢材强度对扭矩-应变关系曲线带来的影响,本文选取直径为133 mm、厚度为4.5 mm、混凝土强度为30 MPa 但钢材强度不同的圆钢管混凝土进行参数分析。由图10(a)可知,因混凝土对抗扭刚度贡献不是很大,圆钢管混凝土在钢管屈服前基本上处于线弹性阶段,随着钢材强度的增加,钢管的屈服剪应变随之增加,试件的弹性阶段也随之增加。随着钢材强度的增加,钢管的抗剪强度随之增加,在钢管屈服后阶段对混凝土的围压也随之增加,使得有利的附加扭矩T2得到增加,试件在0.01ε 处试件的抗扭承载力也越大。由图10(b)可知,钢材强度增加得越快,增加率减少得越慢。
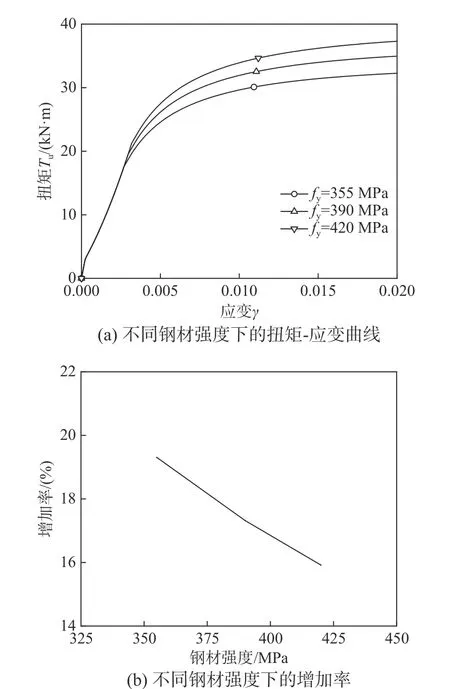
图10 钢材强度对扭矩-应变关系的影响Fig. 10 Influence of steel strength on torque-strain relationship
4.3 含钢率
圆钢管混凝土的含钢率与钢管直径D和厚度t有关,为研究含钢率对扭矩-应变关系曲线带来的影响,本文选取直径为133 mm、混凝土强度为30 MPa,钢材强度为324.34 MPa、含钢率等差设置的圆形钢管混凝土进行参数分析。由图11(a)可知,因试件的抗扭刚度主要由钢管提供,含钢率越高的试件在钢管屈服前阶段的抗扭刚度越大。随着含钢率的增加,试件的抗扭承载力因钢管的抗扭能力和附加扭矩T2的提高也在逐步增加。在钢管屈服后阶段,不同含钢率的扭矩-应变曲线趋于平行,说明提高含钢率对抗扭承载力的提高有限。由图11(b)可知,增加值随含钢率的增加而减少得越快。
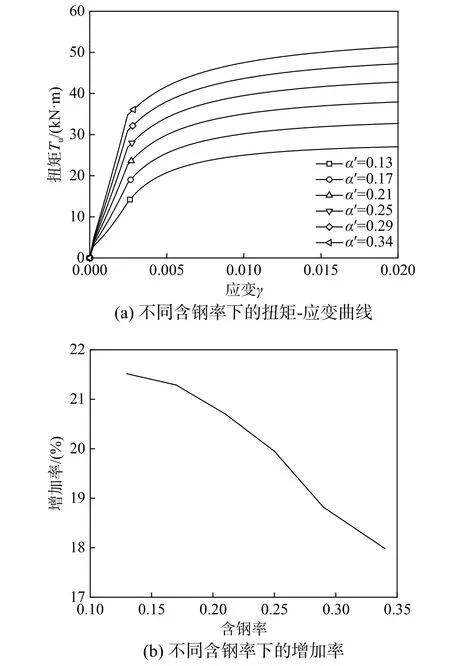
图11 含钢率对扭矩-应变关系的影响Fig. 11 Influence of Steel ratio on torque-strain relationship
4.4 钢管直径
为说明钢管直径对扭矩-应变关系曲线带来的影响,本文选取含钢率为0.15、混凝土强度为30 MPa、钢材强度为324.34 MPa、钢管直径等差设置的圆形钢管混凝土进行参数分析。由图12(a)可知,随着钢管直径的增加,试件的抗扭刚度得到显著提高。钢管直径的等差增加使得试件的抗扭承载力增加得越快,附加扭矩T2给试件带来的增加值也显著增加得越快。由图12(b)可知,增加率随钢管直径的增加而不发生变化。
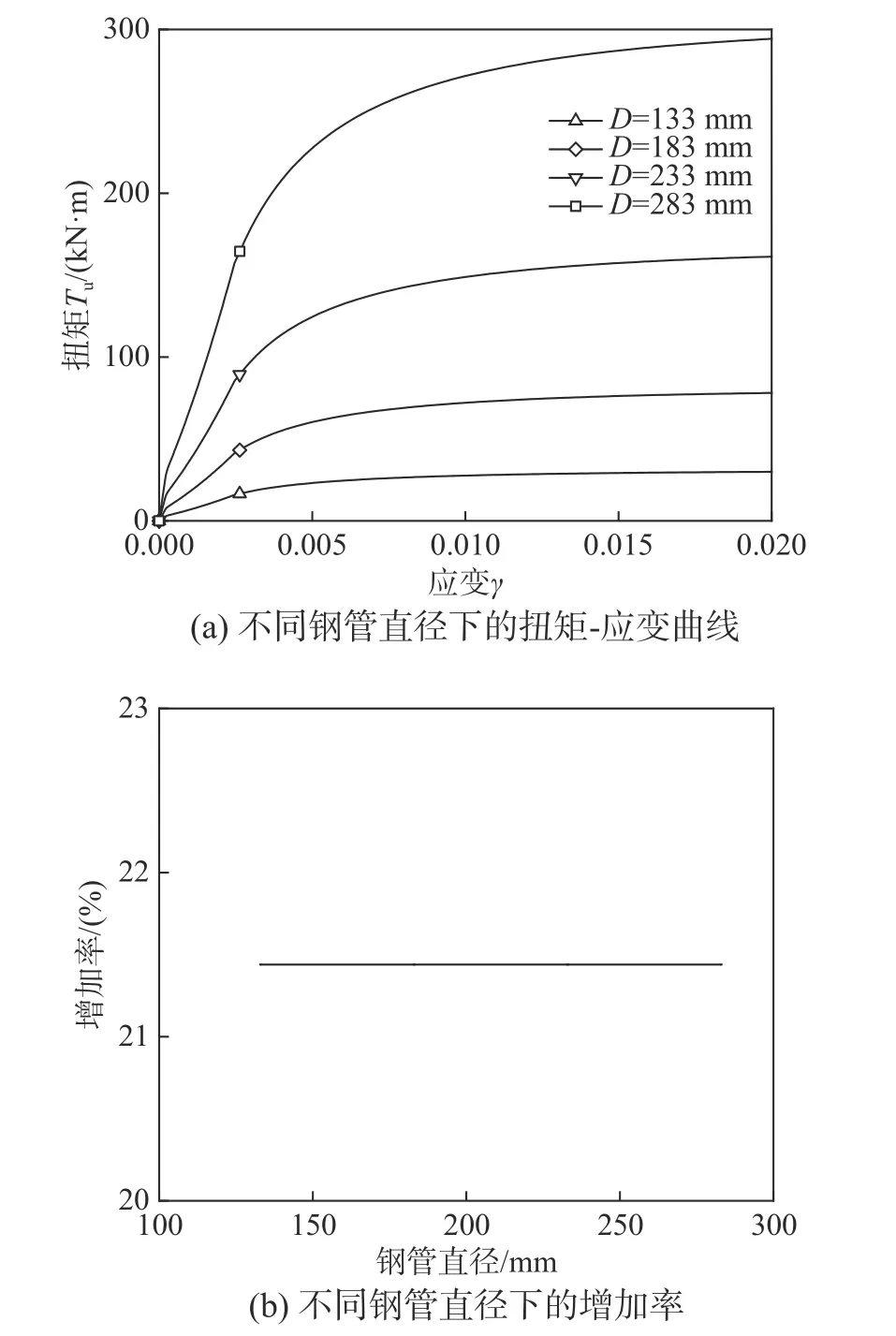
图12 钢管直径对扭矩-应变关系的影响Fig. 12 Influence of steel pipe diameter on torque-strain relationship
综上所述,在实际工程应用中为达到经济适用性,宜采取较低混凝土强度、较大钢管直径的圆钢管混凝土来承担扭矩。在对钢管直径有限制的工程中,为使得结构的强度较大、变形较少同时充分发挥组合材料的性能,在含钢率较低的情况下宜增加钢管厚度,而在含钢率较高的情况下宜增加钢材强度。
5 结论
本文对圆钢管混凝土在自由扭转作用下进行了受力分析,得到以下结论:
(1)基于统一强度理论,建立了混凝土抗剪强度与混凝土圆柱体抗压强度之间的关系、钢材抗剪强度与屈服强度之间的关系。此外,建立了弹性阶段钢管混凝土切应变与正应变之间的关系。
(2)将圆钢管混凝土在自由扭转下的全过程分为混凝土开裂前、钢管屈服前和钢管屈服后这三个阶段,通过对这三个阶段钢管和混凝土受力状态和相互作用的分析,提出了圆钢管混凝土在自由扭转作用下扭矩-应变分段式理论模型,较好地吻合了试验结果。该理论模型计算简便、概念明确并且能够定量地指出钢管和混凝土之间的相互作用。
(3)基于本文中得到的理论模型,考虑实际工程中的应用,提出了圆钢管混凝土在自由扭转作用下的抗扭承载力计算公式,计算结果与试验结果之比的平均值为0.996,标准差为0.0579,表明了此计算公式的正确性。该计算公式适用于钢材强度小于528/α3MPa、混凝土强度小于70 MPa的圆钢钢管混凝土,材料的尺寸和力学性质获取方便,便于在实际工程中的应用。
(4)在本文理论模型验证的基础上,分析了钢材强度、混凝土强度、含钢率和钢管直径对钢管混凝土抗扭性能的影响,研究表明:混凝土强度对抗扭承载力影响不明显;随着钢材强度的提高,试件弹性阶段增加,抗扭能力也得到了提高;随着含钢率的增加,试件的线弹性阶段刚度增大,构件的承载力也得到了提高。随着钢管直径的增加,试件的线弹性阶段刚度和抗扭承载力得到了显著的提高。

