钢铁企业煤气消耗设备时序优化研究

任明远，姜明军，周海军，陈思行，殷捷，顾江其

(1.国网甘肃省电力公司，兰州 730000；2.南京瑞松信息科技有限公司，南京 210038)

我国是世界上最大的钢铁生产国，钢铁行业作为能源消耗密集型行业，面临着较大的节能减排压力。钢铁企业在生产钢铁的同时，会产生大量的煤气副产品，将钢铁富余煤气用于额外生产或者发电，是提高能源利用率、降低钢铁生产成本的有效手段。但钢铁企业的副产品煤气具有连续性和波动性的特点，常常出现煤气的产出与消耗不相匹配的问题，这不可避免的就会造成能源的大量浪费[1-3]。

对副产煤气的合理优化调度会直接影响吨钢煤耗以及钢铁企业的经济效益。国内外学者针对煤气优化调度的具体问题，提出了很多调度算法。谢升等[4]采用混合整数线性规划方法，对钢铁企业的生产电力以及煤气放散量进行优化，结果显示该煤气优化调度模型能够有效提高2.93%的发电量，且在高炉检修之后能够提高22%左右的发电量。孙雪莹等[5]基于模糊机会约束规划方法建立副产煤气系统模糊优化调度模型，通过钢铁企业生产数据验证，提出的规划方法比确定性的方法可靠性更高，同时给出了不同置信区间下能够满足煤气系统模型约束的调度方案，便于调度员做出更好的决策。胡建双等[6]对副产煤气进行放散最小的模型建立，结果验证表明，这样既可确保生产的安全性，同时也对企业副产煤气的合理使用起到积极作用。张超[7]以企业煤气放散和生产成本最小化为目标，在考虑了调度时间段内出现生产变化的情况下，对调度时间进行分段处理，最后通过动态规划的思想对改进后模型进行分析，通过模型求解结果，改进后模型在煤气放散量的回收上优于原模型。

张建良等[8]通过引入燃气-蒸汽联合循环设备，实现了钢铁生产煤气的新平衡，建立了煤气热值的优化模型，结果表示新模型能够有效减少煤气生产能耗。

由于煤气消耗设备的频繁启停会造成设备的使用寿命下降和运维成本增加，本文选取煤气消耗设备的启停次数变化最小为优化目标之一。另外，当园区电厂的输入能量波动较大时，对园区电厂的运行稳定性会造成较大的影响，因此本文将园区电厂输入能量的波动作为另一个优化目标。综合上述两个优化目标，本文提出以煤气消耗设备时序优化为主，园区电厂调节为辅的优化调节方法。

1 研究对象

本文研究对象为某钢铁企业，该企业煤气系统设备如表1所示，副产煤气系统如图1所示。

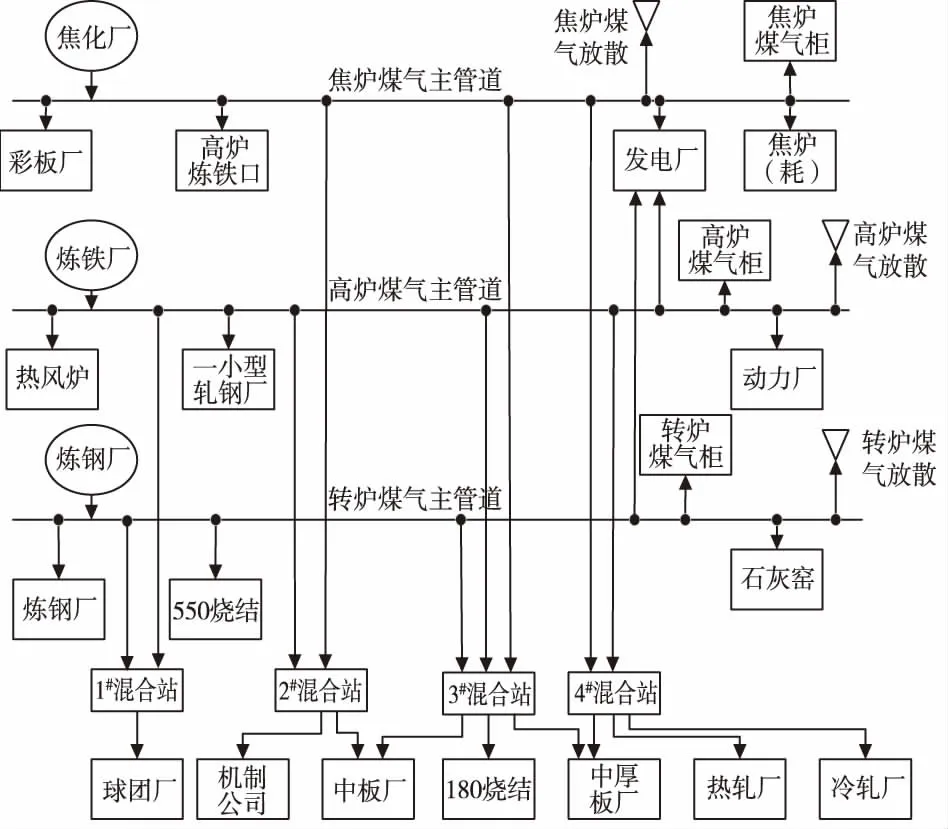
图1 某钢铁企业副产煤气系统图

表1 某钢铁企业煤气系统设备

钢铁企业副产煤气长时间处于产耗不平衡的状态，通过对煤气消耗设备优化和合理的安排煤气消耗设备的启停，能够有效降低煤气消耗设备的启停次数，同时能够减小园区电厂输入热量波动，提高整体系统运行的稳定性与安全性。

本文在进行时序优化时，假设煤气生产设备和煤气消耗设备全天候运行，以煤气生产设备为产气端，煤气消耗设备为耗气端，对煤气消耗设备进行时序优化。园区电厂热值与热量满足约束如式1所示。

(1)

式(1)中，h为热值，kJ/m3，hmax为17 298 kJ/m3，hmin为3 812 kJ/m3；Q为热量，GJ/h，Qmax为4 988 GJ/h，Qmin为2 001 GJ/h。

2 煤气消耗设备的再分类

本研究的钢铁企业中共有16个煤气消耗设备，但由于部分煤气消耗设备与生产紧密关联，将参与优化的设备分为两种。第一种，固定不可调节消耗设备，这些设备由于在炼钢炼铁过程起着关键作用(热风炉、炼铁厂设备、动力厂设备、炼钢厂设备、焦化厂设备)或者生产周期固定，无法灵活调节(彩板厂设备、冷轧机厂设备)，故不参与煤气消耗设备时序优化；第二类，不固定可调节消耗设备，该类设备由于生产的启停不影响钢铁的生产，生产相对独立，主要是冷轧机、550烧结炉、轧钢机、石灰回转窑、烧结球团厂设备、中板厂设备、180烧结炉、中厚板厂设备、热连轧机和机制砂公司设备，因此本次时序优化研究主要是针对上述设备。

2.1 不参与时序优化的煤气消耗设备

第一类煤气消耗设备由于在钢铁生产的工艺流程中承担着重要的角色，其运行时长需要与焦炉、高炉和转炉的运行时长相同，所以无法参与时序优化。第一类设备运行时间以及煤气消耗量如表2所示。

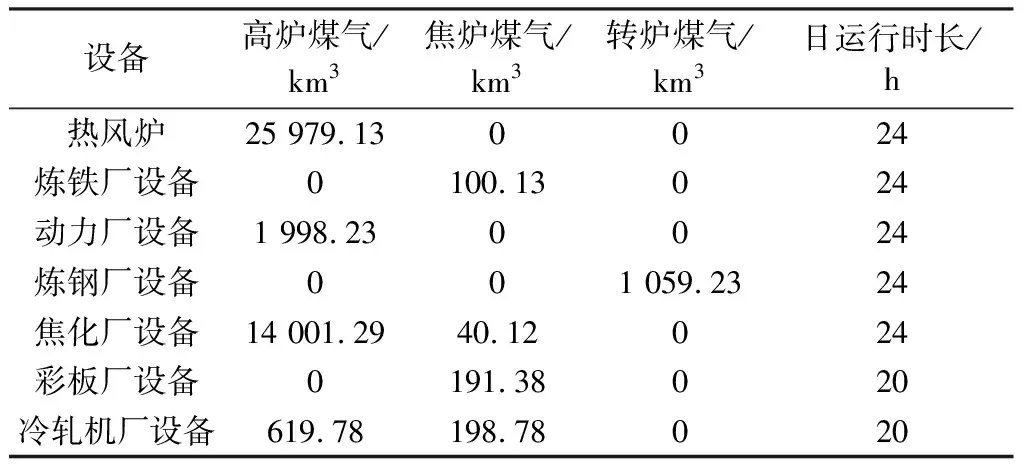
表2 第一类设备运行时长以及煤气消耗量

2.2 参与时序优化的煤气消耗设备

参与时序优化的煤气消耗设备无法直接获取，本文通过历史数据中设备每小时煤气消耗体积，得到各煤气消耗设备的每日正常运行时长，第二类设备运行时长及煤气消耗量如表3所示。

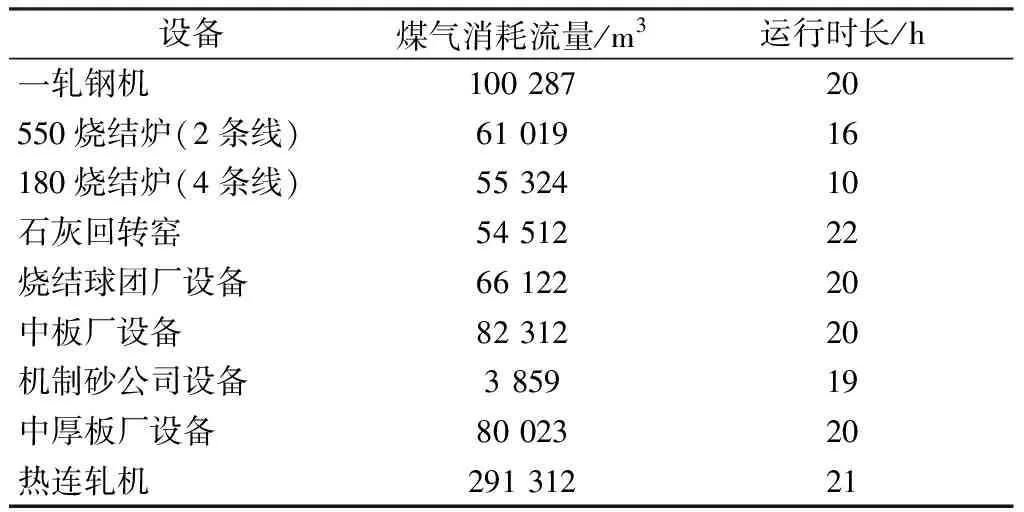
表3 第二类设备运行时长及煤气消耗量

第二类设备的煤气消耗动态模型，如式(2)所示：

(2)

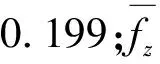
3 园区电厂的消耗特性

本文时序优化时，优先满足煤气消耗设备的供应，剩下的煤气分配给园区电厂。煤气消耗实际共有二十条线(其中550烧结炉有两条生产线、180烧结炉有四条生产线)当所有煤气消耗设备的需求都被满足之后，富余煤气输入进园区电厂，在优化过程中，通过控制设备的启停，得到输入园区电厂的热量，并对热量进行热值和热量判断。富余煤气的热值、热量需要满足式(1)中所描述的最大值与最小值。因此园区电厂煤气消耗模型建立中，需要优先计算各个时段进去园区电厂的热量与热值，其中热值需要通过体积与热量求得，因此额外建立各时段的富余煤气体积模型。

3.1 各时段富余煤气热量模型

生产的煤气总热量除园区电厂消耗的热量之外就是供给煤气消耗设备的热量，因此园区电厂消耗的热量等于煤气系统产生的总热量减去煤气消耗设备单位时间区段消耗的总热量，园区电厂消耗的富余煤气热量可以用式(2)来表示，煤气消耗设备的数量根据上述分析共20个。

Qi=hbfgfsum_bfg_i+hcfgfsum_cfg_i+

(3)

式(3)中，Qi表示园区电厂第i小时内消耗的富余煤气热量，kJ；i∈[1,24]且为整数，表示每日中的各个时间段；fsum_bfg_i、fsum_cog_i、fsum_cfg_i分别表示高炉、焦炉、转炉第i小时内产生的煤气总体积，m3；fcon_j表示煤气消耗设备j第i小时内消耗的煤气体积，j=1，2，3…20表示为各个煤气消耗设备生产线；hi表示对应煤气消耗设备第i小时内消耗的煤气平均热值，kJ/m3。

3.2 三种富余煤气体积模型

在实际生产中，会出现煤气消耗设备中转炉煤气供应不足的情况，此时会将高炉煤气(热值低)与焦炉煤气(热值高)混合，让煤气消耗设备使用，然后再将剩余的煤气送入园区电厂。

fbfg+fcog=fcfgfbfghbfg+fcoghcog=fcfghcfg

(4)

根据热力学第一定律和质量守恒定律解得：

(5)

式(4～5)中，Pcog和Pbfg分别表示焦炉煤和高炉煤气在混合煤气中所占比例；fcog、fcfg和fbfg表示各成分煤气的体积，m3；hcog、hcfg和hbfg分别表示焦炉煤气、转炉煤气和高炉煤气的热值，kJ/m3。

煤气消耗设备的需求被全部满足以后，按照式(6)～(11)计算输入园区电厂中的各成分煤气的混合体积含量。

(6)

(7)

(8)

(9)

(10)

(11)

式(6～11)中，fcfg_before_i表示采用高焦炉煤气替代转炉煤气之前，第i小时进入园区电厂的转炉煤气的体积，m3；Pcfg_ j、Pbfg_ j、Pcog_ j分别表示第j个设备在第i小时内消耗的煤气中转炉煤气、高炉煤气、焦炉煤气所占的体积份额。fcfg_i、fcog_i、fbfg_i分别表示第i小时输入园区电厂的转炉煤气、焦炉煤气、高炉煤气体积，m3。fcon_cfg表示转炉煤气不足部分采用高焦炉煤气替代时所需的焦炉煤气体积，fbfg_cfg表示转炉煤气不足部分采用高焦炉煤气替代时所需的高炉煤气体积，m3；F替代为高焦炉煤气利用式(5)替代转炉煤气时，转炉煤气体积与高炉、焦炉煤气体积之间的函数关系。

3.3 富余煤气热值

由式(4)～式(11)可得园区电厂的输入煤气热值如式(12)所示：

(12)

式(12)中，h电厂_i为第i小时输入园区电厂的混合煤气的热值,kJ/m3。

4 煤气消耗设备优化模型

4.1 决策变量

根据第三章分析，本文所选取的钢铁企业仅有9个煤气消耗设备(13个生产线)参与优化，所以本文选取能够启停的设备数量按照13进行处理。

假设每个煤气消耗设备单次运行时间长度为1 h，则13个煤气消耗设备每日24 h内共有13×24=312个小时区间。根据表3中的第三列数据相加可知(550烧结炉按2个设备计算，180烧结炉按4个设备计算)，13个煤气消耗设备每日正常工作时长总计为214 h。

假设设备正常工作状态用“1”表示，非正常工作状态用“0”表示，本文建立一个13×24的设备运行状态矩阵Z，矩阵中元素的值Zji表示第j个设备在第i小时内的设备运行状态，值为0或1。由于表3中的第三列设备每日需要正常运行的总时长为214 h，则矩阵中一共存在214个元素值为1，另有98个元素值为0。

对于优化模型，变量的选取直接影响优化问题的复杂程度和求解难度，根据本文上述的模型分析，给出以下四种决策变量选取方案：

方案一：设备运行状态矩阵中所有元素全部用一个变量表示，一共需要312个决策变量。

方案二：以设备运行状态矩阵中元素值为“1”的位置为变量，即每个设备正常运行时间的位置作为变量，一共需要214个决策变量。

方案三：与方案二类似，以矩阵元素中值为“0”的元素的位置作为变量，该方式选取变量共有98个。

方案四：观察表3可以看出，180烧结设备4条工作线的正常运行时间小于非正常运行时间(10<14)，所以为了进一步减少计算复杂度，180烧结设备四条线可以选择矩阵中元素值为“1”的位置为变量，共计40个决策变量(单线10个)，其它设备以“0”为变量，共计42个决策变量(每个设备非正常运行时长为24减去正常运行时长)，这样共计需要决策变量82个。

例如由表3中第3列设备日际正常运行时长可知，轧钢机每日需要正常运行20 h，保温4 h；如果采用方案一，全天24 h各需要一个变量，石灰窑共需要24个变量；如果采用方案二，需要20个变量来表示运行的22 h的位置；采用方案三则只需要4个变量，分别记录保温的4 h各在24 h中的位置，在5点到7点保温一次，14点到16点保温一次时，4个变量分别为6、7与15、16。

优化时候，优先选择决策变量少的方案，这样有利于优化模型的计算与求解，本文采用方案四的变量设计方案，选取82个变量，设计如表4所示，其中xk∈[1，24]，k∈[0，81]，xk与k都为整数。

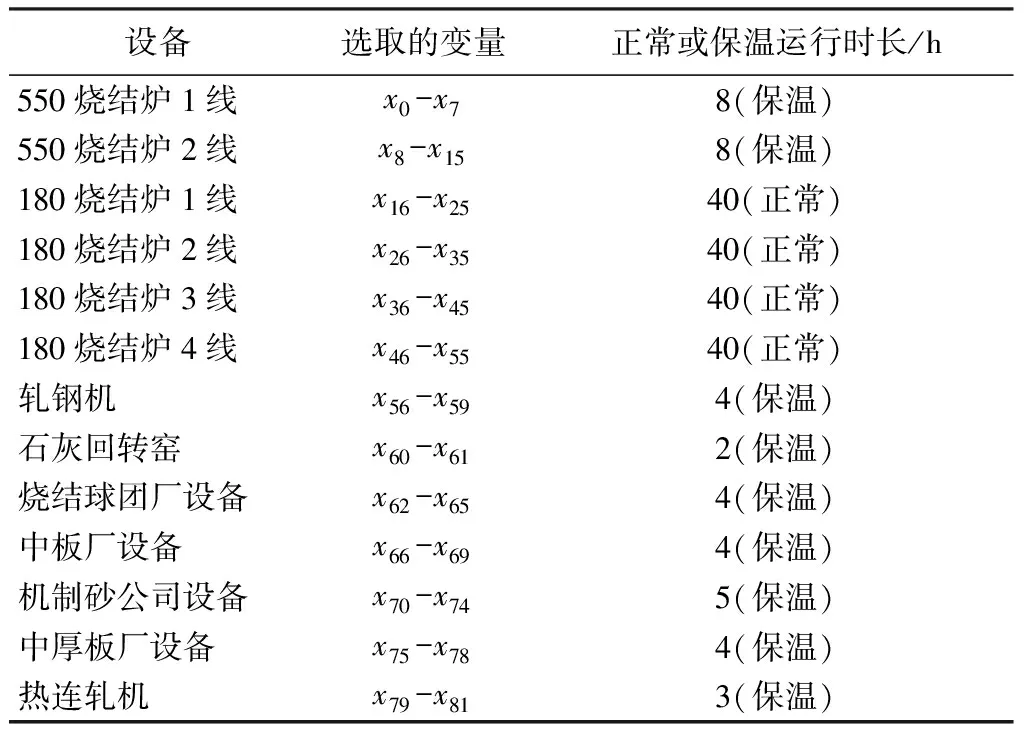
表4 决策变量

4.2 优化目标

为了保证系统运行的稳定性与安全性，本文选择园区电厂输入热量波动最小化和煤气消耗设备运行状态变动次数最少为优化目标。

(1)园区电厂输入热量波动最小化，由于最后4 h冷轧机设备无消耗，故输入热量按照两个区间计算热量波动。

(13)

式(13)中，Qaverage_1表示园区电厂每日前20 h的平均输入混合煤气热量，kJ；Qaverage_2表示后4 h的平均输入混合煤气热量，kJ。

(2)煤气消耗设备启停改变次数最小化。本文通过建立一个13行24列的设备的运行状态分布矩阵Z，通过将各个设备后面时间段的设备状态减去前面时间段的设备状态的差全部相加最小作为优化目标。

(14)

式(14)中，zj,i+1、zj，i为第j个设备分别在第i+1个小时、第i个小时中的状态，1表示正常运行状态，0表示非正常运行状态。

4.3 约束条件

本文运行策略优先考虑煤气消耗设备的煤气需求，剩余煤气再输入园区电厂，只要考虑进入输入园区电厂是否能够满足需求。

(1)单位时段中，园区电厂的输入混合煤气热量和热值需要在式(1)中的热值和热量最小值与最大值之间，这样表示煤气消耗设备已经能够优先满足。

假设d表示为违反约束程度，则式(15)和(16)分别表示输入园区电厂的热值和热量的违反约束程度。

df1i=(|hi-hmin|+|hi-hmax|-(hmax-hmin))2

(15)

df2i=(|Qi-Qmin|+|Qi-Qmax|-(Qmax-Qmin))2

(16)

式(15)和式(16)中，df1i、df2i分别表示输入园区电厂的混合煤气热值与热量违反约束程度；hi、hmin、hmax分别表示第i小时输入园区电厂的混合煤气热值、煤气热值最小值和最大值；Qi、Qmin、Qmax分别表示第i小时输入园区电厂的混合煤气热量、热量下限和热量上限。

(2)在运行方案中，当煤气消耗设备所需转炉煤气不足时，则采用高炉煤气与焦炉煤气的混合气。在时序优化中，需要优先满足煤气消耗设备的不停产，因此当高炉煤气量与焦炉煤气量大于0时，表示当前的煤气消耗设备的需求量已经满足。

(17)

假定df3i，df4i为高焦炉煤气输入电厂流量违反约束程度，如式(18)和(19)所示，总的约束违反程度函数F如式(20)所示：

(18)

(19)

(20)

5 优化算法

遗传算法(Genetic Algorithm，GA)是进化算法的一种，通过模拟达尔文进化论中的自然选择和遗传学机理的生物进化来建立计算模型。在计算较为复杂的优化问题中，遗传算法相较于普通的优化算法，能够快速地获得比较好的优化结果，因此本文的研究采用遗传算法继续分析。

5.1 基因的设计

本文选择13个煤气消耗设备的正常运行时间段作为决策变量，按照表4中的设计方式设计优化方法的基因。表4中共有82个决策变量，建立相应的遗传算法基因X0-X81，每个基因的取值为对应的设备保温状态或正常运行所在的时间，即Xk∈[0，23]，k∈[0，81]。

运行优化的基础是保证当日分配给煤气消耗设备的煤气能够消耗完全，所以增加煤气消耗设备的等式约束，但同时也增加了模型的求解难度。在本研究中，为降低模型求解的复杂程度，在个体初始化和交叉变异的过程中，优先判断个体是否满足运行时间。

5.2 基因的约束处理

以中板厂为例，中板厂设备停运时间为4 h。

(1)初始化：首先4个个体基因(X66～X69)随机初始化整数，范围在0～23之间，如果出现相同的整数，则重新生成，直到4个整数均不相同。

(2)交叉(变异)：将中板厂4个基因位置中的任意两个进行交叉变异产生新的4个基因，并按照数值大小进行排序。新个体的中板厂基因位置的基因排序见表5, 表中数值表示中板长的每日保温运行所在的时间。

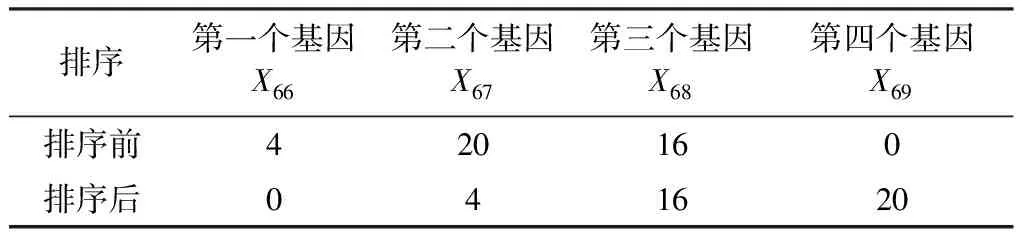
表5 新个体的中板厂基因位置的基因排序

新产生的基因需要保证中板长4个基因无重复数值，否则不能满足中板长每日保温时长4 h的条件。对4个基因加上约束，当各基因的数值超出约束边界范围的时候，将该基因数值置为边界数值，新个体中中板厂基因位置的基因约束见表6，即后一次保温时间段至少要比前一次保温时间段晚1 h。

表6 新个体中中板厂基因位置的基因约束

5.3 约束条件的处理方法

按照模型约束条件和约束违反程度计算式，分别计算个体在优化中的违反程度的大小，最后按照违反程度大小排序，排在最前面个体则越可能是最优解。

本文的遗传算法在选择个体的环节中同时采用约束违反程度排序等级和个体非支配排序等级两个参数共同决定个体优劣的方法。本研究问题中约束较多，可行解不易寻找，所以目标函数值权重设为0.3，违反约束程度权重设为0.7。

6 优化结果分析

将约束条件以及目标函数带入遗传算法中进行计算，设繁衍代数为10 000，种群大小为100。在5次优化之后，得出5次优化的最优解集合，共计500个个体，然后确定其中的可行解，满足约束的双目标可行解如图2所示。非劣解的日际目标函数与约束违反程度见表7，满足约束的双目标非劣解如图3所示。

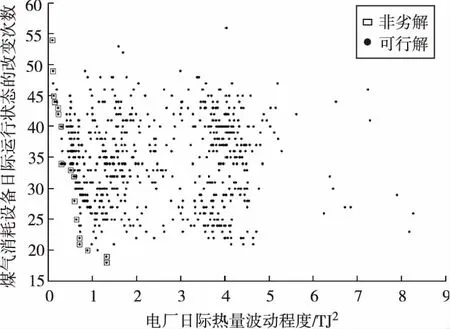
图2 满足约束的双目标可行解

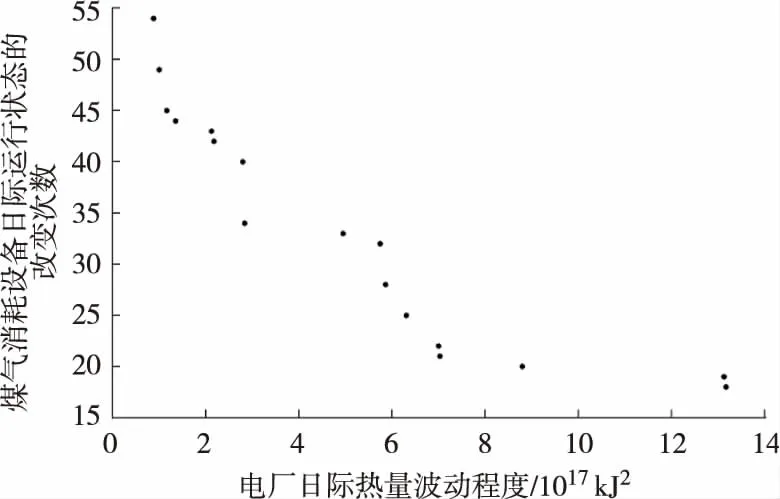
图3 满足约束的双目标非劣解

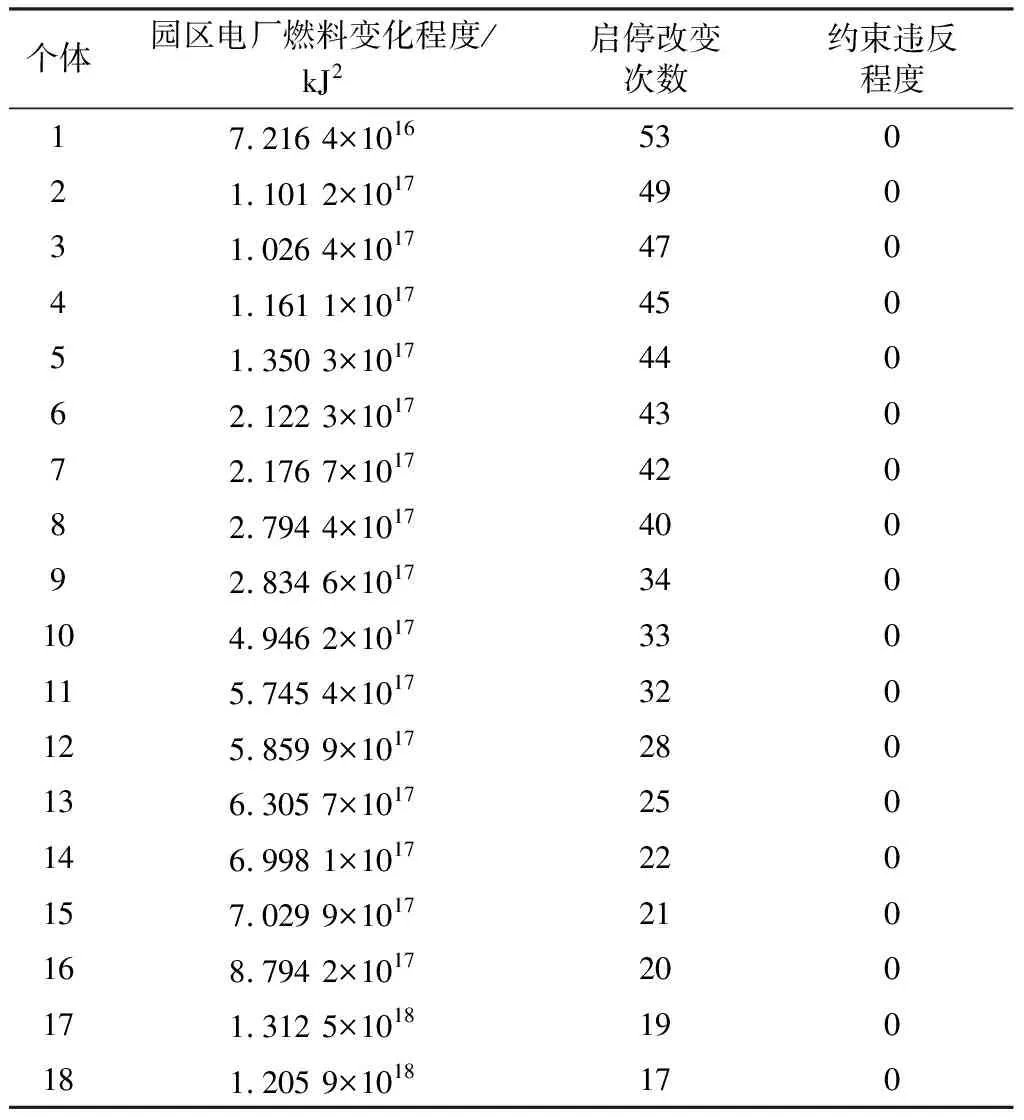
表7 非劣解的日际目标函数与约束违反程度

由于这些个体之间的优化目标都存在各自的优缺点，故这15个个体之间没有明确的优劣之分。

选择表7中两端两个个体的时序优化结果展示如表8和表9所示。表8对应结果约束违反程度为0，热量波动程度为1.205 9×1018kJ2，运行状态改变次数为17次；表9对应约束违反程度为0，热量波动程度为7.216 4×1016kJ2,运行状态改变次数为53次。表中第一列A～M依次表示表3中的13个煤气消耗设备，第一行为时间，表中0代表设备保温，1代表设备正常运行。

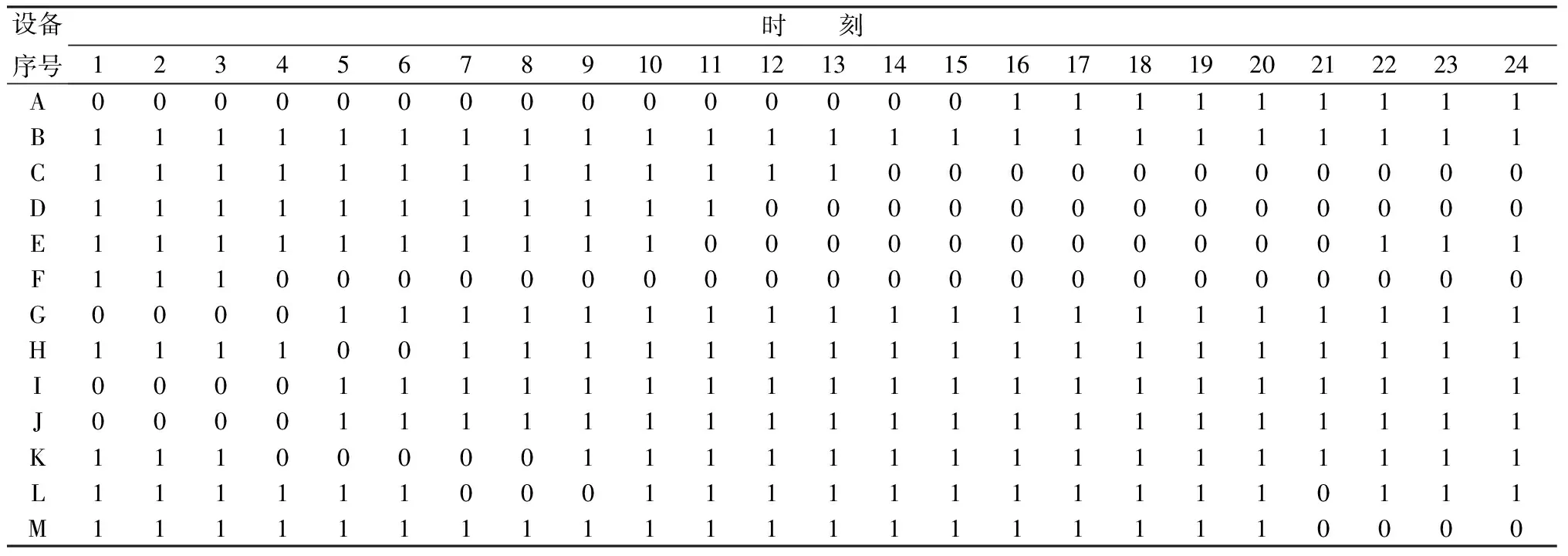
表8 非劣解中设备启停改变次数最小的优化解

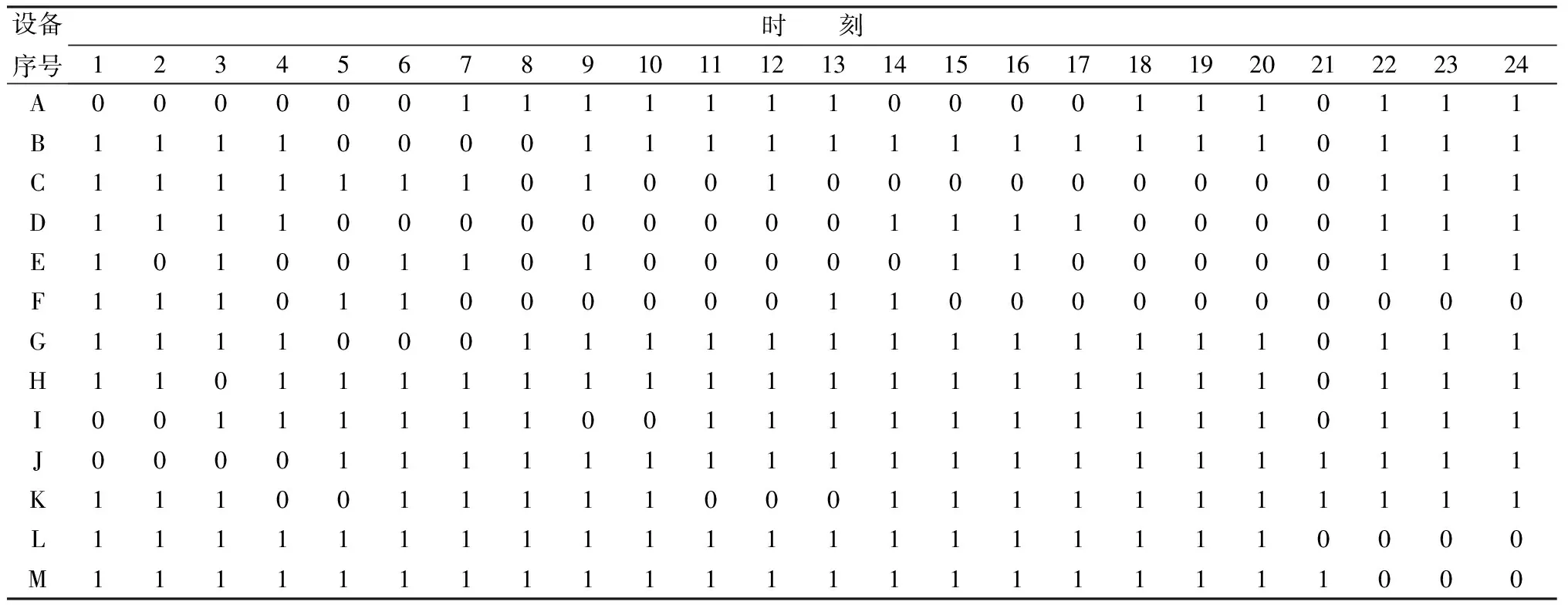
表9 非劣解中园区电厂输入燃料变化最小的优化解

图3右下角的优化解对应的是表8中的内容，此时违反约束程序函数F等于0，表示输入煤气被全部消耗，没有煤气浪费，且没有煤气消耗设备停工停产；此时设备运行状态改变次数只有17次，平均每个设备每日只改变不到2次运行状态。但此种运行方式会导致园区电厂输入热量的波动较大。

图3左上角的优化解对应的运行时序结果如表9所示，此时与上述优化结果类似，违反程度函数F为0，同样没有输入热量的浪费，此时园区电厂的输入燃料的流量变化较小，此时设备的运行启停改变次数达到53次。

两种时序下的园区电厂每小时输入燃料波动如图4所示。此时，园区电厂在两个优化解下的每小时输入的热量及热值均满足约束条件。两个优化解的目标不一样，一个尽可能的减少煤气消耗设备的启停改变次数；一个尽可能的降低园区电厂的输入燃料变化，但是却导致了煤气消耗设备的运行状态频繁变化。

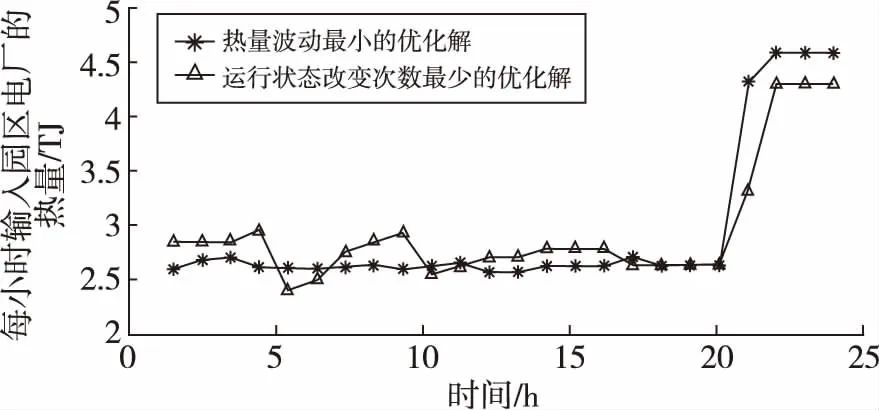
图4 两种时序下的园区电厂每小时输入燃料波动

通过将时序优化结果中燃料波动工况最小的电厂输入和实际运行数据分别做处理之后，实际运行方差为0.008 21，优化解的园区电厂的波动方差为0.000 226 7，相较于实际波动降低97.59%，园区电厂实际运行与优化运行方式热量波动比较如图5所示。从图5可以看出，通过本文的时序优化之后，大大地降低了热量波动程度。

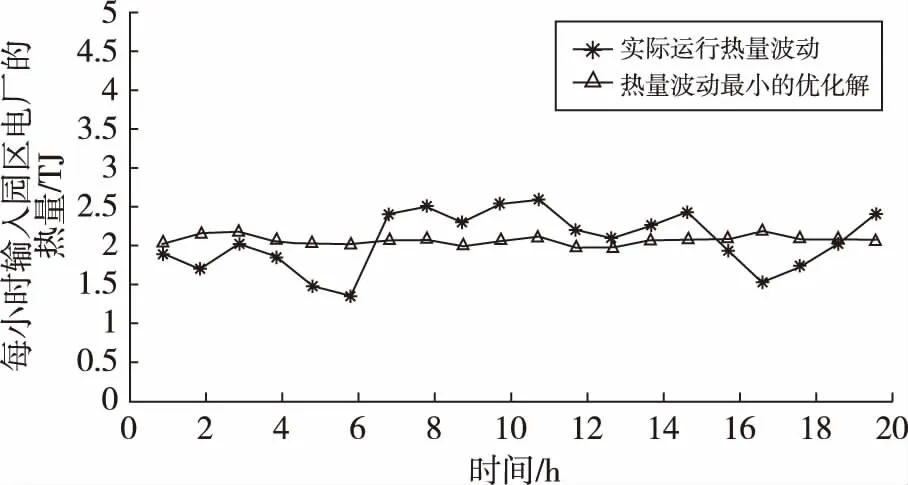
图5 园区电厂实际运行与优化运行方式热量波动比较

7 结语

本文在钢铁企业原有煤气柜和园区电厂等传统调度手段之外，提出了一种新的煤气时序优化方法作为原有传统调度手段的补充。本文将所研究的钢铁企业中现有的煤气消耗设备按照是否能够灵活启停分为两种，并建立了不同煤气消耗设备和园区电厂的设备模型。文中以园区电厂输入燃料变化最小，煤气消耗设备启停状态改变次数最少为优化目标，通过遗传算法进行优化。

在采用多目标遗传算法对参与时序优化的煤气消耗设备进行优化时，文中提出一种改进基因设计方式，首先确定每一行基因的个数，然后判断当前行中，“0”与“1”的个数，当“0”小于“1”时，选择以“0”的位置作为决策变量，反之亦然。该种方法的基因设计，能够大大减低基因维数，减少模型的求解难度。优化结果表明，基于上述决策变量的优化模型所求结果可以优先保证煤气消耗设备的燃气消耗，同时能够保证煤气消耗设备的运行状态改变次数较少以及园区电厂的输入热量的波动较小。