基于等温度线相似换算的全包线控制改进方法研究

张冬冬，刘子赫

(1.中国航空发动机集团有限公司，北京 100097；2.南京航空航天大学能源与动力学院，南京 210016)

随着现代控制理论研究不断的发展和深入，学者们提出了诸如H∞、增广LQR等控制器设计方法[1]。然而，这些先进控制算法多数是基于线性系统的控制理论，对于航空发动机这一强非线性被控对象，在实际工程应用中的控制效果并不十分理想。传统闭环PID控制被控对象特性限制、理论完整技术成熟、参数整定过程也相对简单方便[2]。因此，国内外航空发动机控制系统中，应用最广泛的依然是传统的经典PID控制。航空发动机工作条件多变且复杂，在不同的飞行条件下进口条件不断发生变化，时间常数和放大倍数在不同飞行条件下差异可能多达几倍,常规固定的控制器参数无法满足发动机在全包线的控制要求[3]，因此，常规PID控制很难保证发动机在所有的工作状态下都有良好的动态特性和稳定性。为此，学者们提出了多种改进方案，不断改进PID控制器的设计方法和参数整定方法[4-5]。

对于全包线PI控制器的设计，近年来主要集中在基于遗传算法[6]或神经网络的全包线PI控制器设计研究[7-8]和自适应PI控制研究。其中，参数自适应PI控制应用是一项十分热门的研究课题，国内外学者开展了大量关于PID控制器参数自适应技术的研究，如专家系统、神经网络、模糊逻辑、灰色理论和遗传算法等，这些算法和经典的PID控制相结合，产生了新型的智能控制器，使PID控制器的效果得到改善，以适应复杂的工况和高质量的控制要求[9]。李鹏远[10]开展了基于相似换算的自适应PI控制仿真验证研究，提升了不同飞行条件下PI控制器的控制效果。李秋红[11]等提出一种基于小波神经网络在线辨识的航空发动机PID控制算法，在线修正PID参数。傅强[12]开展了模糊自适应整定PID控制、基于遗传算法的PID整定和灰色PID 控制等新兴控制理论方法研究并应用于发动机稳态控制中。董劲等[13]针对航空发动机难以建立精确数学模型的特点，提出了发动机模糊PID参数自适应控制方案，得到满意的发动机动态和静态性能。基于相似换算的自适应PI闭环控制，利用航空发动机相似原理[14]，可提升整个飞行包线内PI控制器的控制效果，但是常规相似换算方法在全包线应用过程中存在误差，相似换算精度问题将会影响PI控制器在全包线内的闭环控制效果。

因此，本文基于等温度线相似换算原理开展了涡扇发动机全包线闭环控制改进方法研究，通过等温度线划分飞行包线，提升了包线内PI控制参数的精度，进而提升全包线范围的闭环控制精度和控制效能。

1 常规自适应PI控制

1.1 自适应PI控制原理

航空发动机在全包线内的过渡态工作过程中，可以视为一个强非线性和时变的复杂被控对象。将航空发动机与执行机构视作一个整体作为被控对象开展控制器研究，通过传统PI控制方法，整定PI参数，从而达到预定的控制效果。在PI参数整定过程中，首先需要得到放大倍数Ke，时间常数Te。但发动机工作条件复杂多变，同一组PI参数很难满足发动机在全包线内的控制目标要求。因此，在发动机飞行条件以及工作状态的变化的过程中，Ke与Te也需要随之发生变化。

下面给出一些常用的航空发动机相似换算准则，推导出放大倍数Ke，时间常数Te的相似换算准则：

(1)

(2)

(3)

(4)

(5)

式(1)～(5)中，Nf为发动机风扇转速；T1为风扇进口处总温；Td0为海平面标准大气温度，取值为288.15 K；Wfb为发动机消耗的燃油量；P1为风扇进口处总压；Pd0为海平面标准大气压力，取值为0.101 MPa；下标1表示风扇进口截面参数；下标cor表示相似换算参数标志，*表示为变化率标志。

由放大倍数Ke，时间常数Te的物理意义可得：

(6)

(7)

由此，得到放大倍数Ke、时间常数Te的相似换算准则：

(8)

(9)

图1为自适应PI控制原理图，Tt2为风扇进口总温，Pt2为风扇进口总压。常规自适应PI通过飞行条件确定风扇进口条件。基于式(8)和(9)可获得基于飞行条件的自适应PI参数，进而在全包线范围内修正PI控制器的控制参数，提高控制器控制效果。

图1 自适应PI控制原理图

1.2 自适应PI控制仿真

选取了六个典型工作点开展自适应PI控制仿真试验。图2给出了不同典型工作点下，发动机分别采用自适应PI控制与常规PI控制的动态响应仿真对比。典型工作点仿真试验条件见表1。

图2 不同飞行条件下自适应PI控制

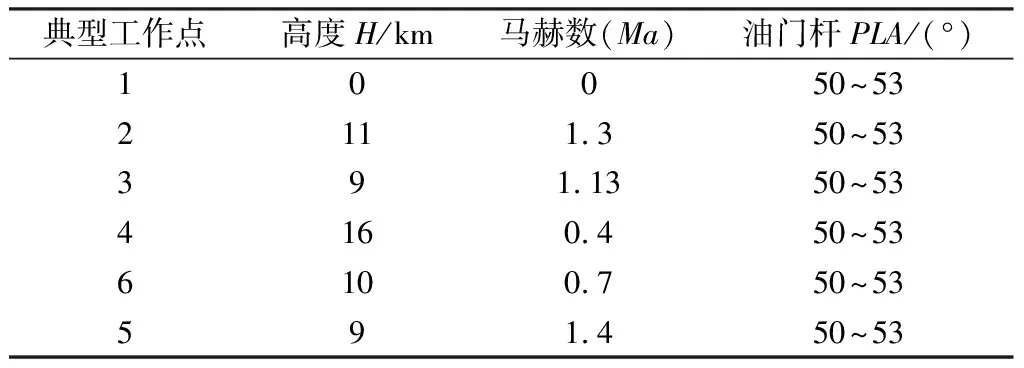
表1 典型工作点仿真试验条件

在H=11 km，Ma=1.3时，采用自适应PI闭环控制，发动机转速出现少量超调(超调量约为0.009%)，响应时间较常规PI闭环控制缩短约4.3 s。在H=9 km，Ma=1.13时，采用自适应PI闭环控制，发动机转速未出现超调，响应时间较常规PI闭环控制缩短4.4 s。由此可见，自适应PI闭环控制在部分包线点可有效提高控制效能，相较于常规PI闭环控制明显得到改善。

在H=16 km，Ma=0.4时，采用自适应PI闭环控制，较常规PI闭环控制，超调量降低了约5.96%，响应时间缩短了约4.44 s，但是仍然存在4.13%的超调量。在H=10 km，Ma=0.7时，采用自适应PI闭环控制，响应时间较常规PI闭环控制缩短了约1.98 s，但是出现了约9.91%的超调量。

仿真结果表明，自适应PI闭环控制在部分包线点有效改善了发动机动态特性和系统稳定性，降低了动态过程中的超调量和响应时间。但是随着飞行高度和马赫数的变化，部分包线点采用自适应PI控制时出现较大超调量等问题。因此，虽然自适应PI闭环控制可在部分包线点提升PI控制参数的精度，进而提升PI控制器的控制效果，但是在部分包线点由相似换算得到的PI控制参数仍然存在一定误差，导致被控量无法达到预期指标，甚至控制效能下降。

2 基于等温度线的闭环控制精度验证

文献[11]针对相似换算精度问题进行了深入的分析和仿真验证，提出了沿等温度线可有效提高相似换算精度的理论。本节将基于此理论开展仿真，验证风扇进口温度对于发动机常规闭环控制效果的影响规律。通过设置等风扇进口温度线上多个仿真试验点，同时选取非等温线上的若干工作点作为对照实验，对比等温度线上的工作点和非等温度线上的工作点处闭环控制效果。为了更好研究等温度线闭环控制的过渡态控制效果，分别开展了小阶跃输入和大阶跃输入的仿真验证。

选取表2所示的等温工作点和非等温工作点，开展小阶跃输入仿真验证。图3给出了分别在等风扇进口温度Tt2工作点1、2下和非等风扇进口温度Tt2工作点3下采用PI闭环控制的小阶跃加速仿真试验结果。

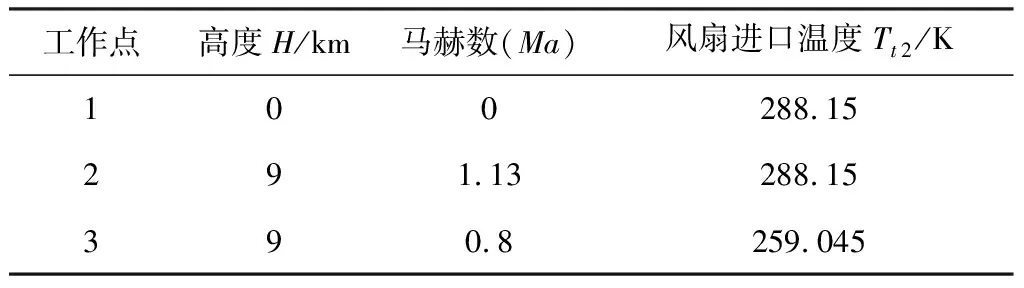
表2 等温工作点与非等温工作点

图3中可见，沿等温度线工作点2的控制效果更为接近同一等温度线地面设计点1的控制效果，非等温度线工作点3处被控量出现明显超调，被控量响应误差相较于等温度线工作点2更大。

图3 小阶跃输入仿真结果

选取表3所示的等温工作点和非等温工作点，开展大阶跃输入仿真验证。图4给出分别在等风扇进口温度Tt2工作点1、2下和非等风扇进口温度Tt2工作点3、4下采用PI闭环控制的大阶跃加速仿真试验结果。

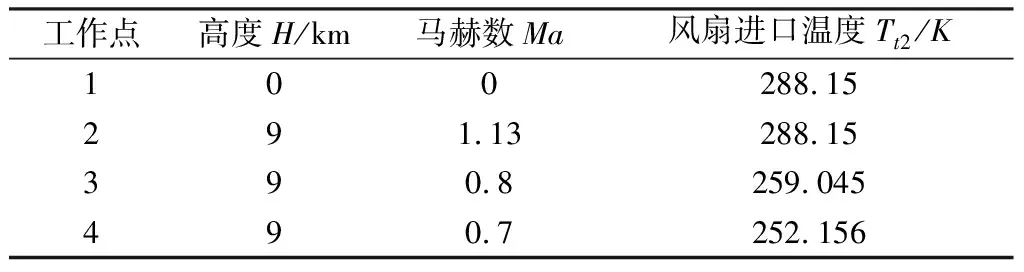
表3 等温工作点与非等温工作点

图4中，沿等温度线工作点2控制效果更为接近同一等温度线地面设计点1的控制效果，随着工作点逐渐远离等温度线，发动机加速响应时间逐渐变慢，控制效能越差。

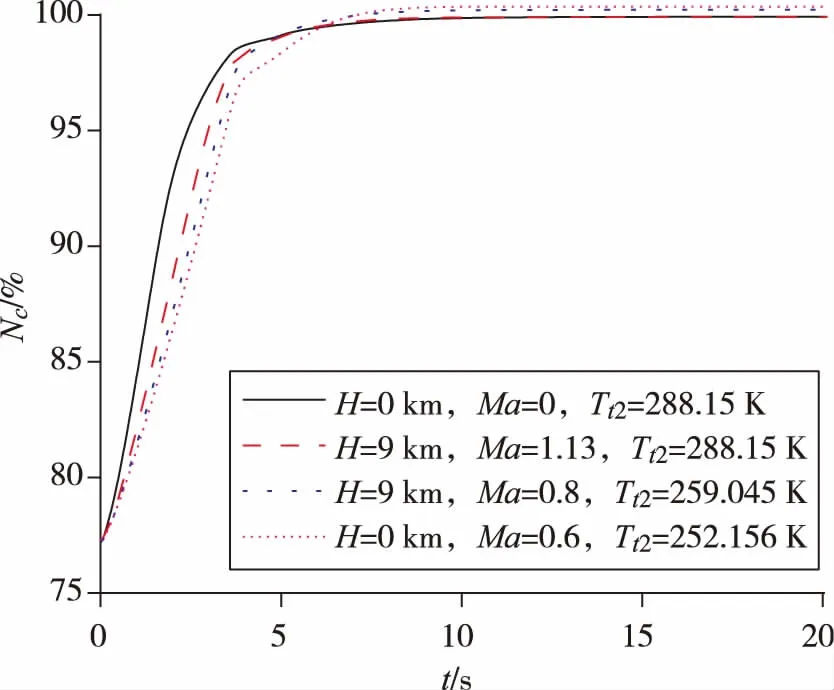
图4 大阶跃输入仿真结果

上述仿真结果表明，发动机等温度线上的各工作点相较于非等温度线工作点相似换算误差更低、控制效果更为接近，随着工作点远离等温度线，闭环控制的控制误差逐渐增大。因此，沿等温度线划分包线开展闭环控制研究，可有效提高全包线内闭环控制的控制精度和效能。

3 基于等温度线的全包线闭环控制

基于上一节的精度验证结果，同一组整定的闭环参数在等温度线上各工作点的控制效果相比于非等温度线工作点更为接近，因此等温度线相似换算理论可有效提升发动机包线内闭环控制的精度。本节基于等温度线相似换算理论，改善常规自适应闭环控制在部分包线点发动机控制效能不佳的问题。

3.1 原理

针对等温度线相似换算误差问题开展了详细的推导与仿真验证，并提出沿等温度线进行相似换算可有效降低因温度对定压比热cp的影响，从而有效提升相似换算精度。基于此等温度线相似换算误差分析理论，在同一条等温度线上的各个飞行包线点之间的相似换算精度更高，在第2小节已通过小阶跃输入和大阶跃输入仿真验证了该方案应用于自适应PI控制的精度优势。因此，基于以上研究，在进行自适应闭环控制器参数整定时，通过等温度线划分飞行包线，基于等温度线的包线划分方案如图5所示。基于等温度线相似换算方法，在不同风扇进口温度线分别整定闭环控制参数，等温度线上任意工作点的闭环控制参数通过相似换算即可适用于等温度线上任意另一工作点。

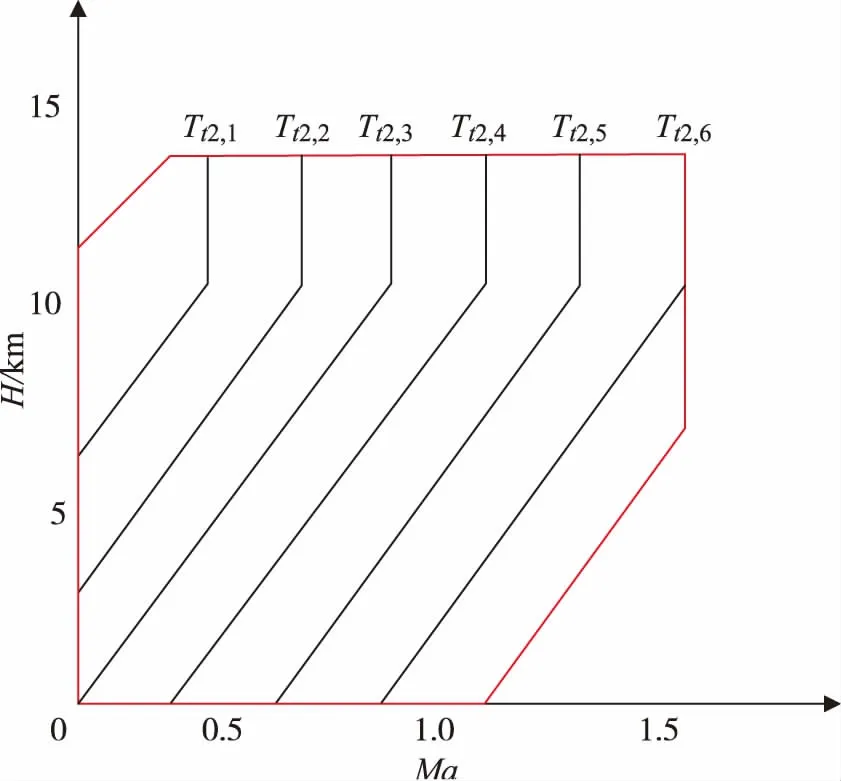
图5 基于等温度线的包线划分方案

为了获得任意包线点的闭环控制参数，本文选取线性插值法，基于已知的临近典型等Tt2下的工作点整定的PI控制参数，基于一维线性插值原理可插值得到未知等Tt2下未知包线点处的闭环控制参数。

选取两条已知等温度线Tt2,1和Tt2,2分别整定得到每条等温度线下的闭环控制参数Kp,1、Ki,1、Kp,2、Ki,2，为了得到Tt2,3下的闭环控制参数Kp,3、Ki,3，首先令：

(10)

得到Tt2,3下的闭环控制参数Kp,3、Ki,3：

Kp,3=Tratio(Kp,2-Kp,1)+Kp,1

(11)

Ki,3=Tratio(Ki,2-Ki,1)+Ki,1

(12)

3.2 仿真验证

选取两条已知的临近等温度线Tt2=240 K和Tt2=288.15 K，同时选取等温度线Tt2=240 K上的典型工作点H=2.4 km，Ma=0.535和等温度线Tt2=288.15 K上的典型工作点H=0 km，Ma=0。分别在两个典型工作点下整定得到两条等温度线上工作点的PI控制参数，通过线性插值得到Tt2=245.019 K下的典型工作点H=10 km，Ma=0的闭速控制参数，各工作点的闭环控制参数见表4。

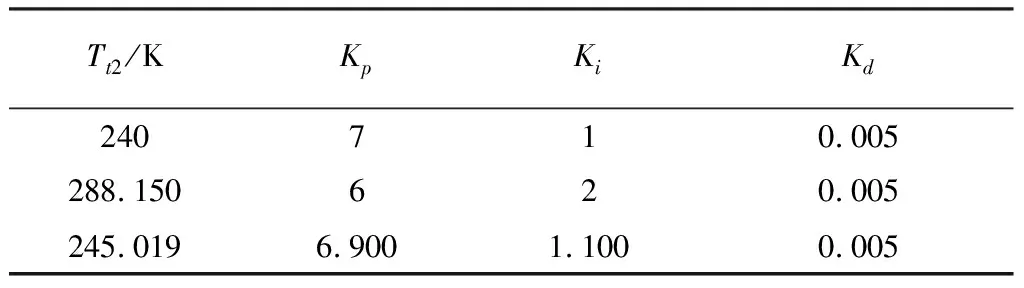
表4 各工作点的闭环控制参数

基于表4所示的闭环控制参数，在各典型工作点开展仿真验证，压气机转速响应如图6所示。

图6中，常规自适应闭环控制下，发动机被控量出现了明显超调；改进的自适应闭环控制下，相较于常规闭环控制发动机被控量响应时间明显缩短，相较于常规自适应闭环控制降低了超调量。仿真结果表明，基于等温线改进的全包线闭环控制方法不仅改善了常规自适应PI控制在部分工作点被控量超调的问题，同时相较于常规闭环控制，发动机被控量在小阶跃输入下的响应时间缩短约3.3 s。

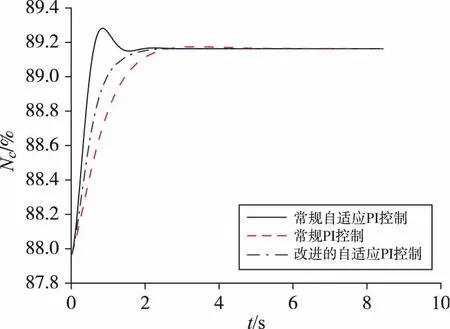
图6 压气机转速响应

4 结语

(1)常规自适应闭环控制方法在部分包线点的控制效果并不理想。本文指出常规自适应闭环控制方法在部分包线点的控制效果无法满足控制目标。

(2)分别开展航空发动机大阶跃和小阶跃加速过程仿真试验，仿真结果表明，沿等温度线划分包线开展闭环控制研究，可有效提高全包线内闭环控制的控制精度和效果。

(3)提出了基于等温度线相似换算理论的全包线闭环控制改进方法。提升闭环控制参数整定精度，进而提升全包线范围的闭环控制精度和控制效果。基于等温度线的闭环控制改进方法减小了常规闭环控制下出现的超调量，同时缩短了被控量的响应时间约3.3 s，有效改善了发动机闭环控制效能。